1. 서 론
2. 마모시험방법
2.1 Pin-on-disk 시험방법
2.2 등간격 나선
3. 아르키메데스 나선 등속도 운동
3.1 등속도 방정식
3.2 나선 등속도 근사해 조사
3.3 고유 상수 및 속도성분
4. 나선 등속도 계산예시
4.1 외향형 나선
4.2 내향형 나선
5. 결 론
1. 서 론
암석절삭 공구(rock cutting tool)는 굴착장비를 구성하는 핵심 도구로서 암석을 직접 압입하여 절삭하는 기능을 한다. 이런 공구부품은 암석절삭 과정에서 고온, 고압상태에서 마찰하중을 받기 때문에 마모와 파손이 빈번히 발생한다. 따라서 공구의 재료로 내마모 성능이 우수한 금속이 사용되는데, 끝단부의 팁은 일반적으로 내마모성이 우수한 텅스텐 카바이드로 구성되고, 나머지 지지부는 강성이 높은 공구강 혹은 열처리 철강으로 구성된다. 이들 공구의 구성재료의 내구성은 공구의 교체시기 및 다운타임에 직접적인 영향을 미치고, 결과적으로 터널의 굴진성능과 밀접한 관계를 지닌다(Robbins, 2000, Hassanpour et al. 2010). 그러므로 설계단계부터 장비에 사용되는 공구 및 재료의 마모특성을 알아야 굴진성능을 정확히 예측할 수 있다.
마모성능을 측정하는 가장 좋은 방법은 터널현장에서 공구의 마모 및 파손특성을 직접 측정, 기록하는 것이다(Farrokh and Kim, 2018). TBM 현장은 각각의 커터에 센서를 설치해서 통해서 지속적인 모니터링을 하고 있다. 하지만, 연속적으로 진행되는 현장의 특성상 중간에 장비를 멈추고 마모도를 측정하는 것이 매우 어렵고, 파손된 공구를 교체하는 시점에 교체된 공구를 회수하여 마모 및 파손정도를 측정하는 불연속적 방법으로 마모도를 평가해야 하는 제약이 있다.
공구를 구성하는 금속재료의 마모를 측정하기 위한 몇 가지 실내시험법(Cerchar, LCPC, NTNU)이 사용되고 있다(Alber et al., 2013, ASTM, 2010, Thuro et al., 2007, Nilsen et al., 2006). 이들 실내시험법은 해당 금속재료를 추출한 특정형태의 시편을 실제하중보다 낮은 하중을 가하여 마모되는 정도를 측정하는 간접적인 시험법이다. 따라서 별도의 마모지수를 구한 후 실제 마모량과 비교하는 현장시험이 반드시 수반되어야 한다.
한편, ASTM은 금속재료의 마모시험방법으로 4가지 마모시험 형태를 제안한 바 있다(ASTM G99). 이 방법중 pin-on-disk 시험법은 공구가 원판형 모재의 표면을 일정한 나선궤도를 그리면서 접촉하는 형태를 설명하고 있다. 따라서 암석절삭공구의 직접 마모시험법으로 적합할 것으로 판단되었다. 그래서 본 연구는 해당 시험방법의 등속도 나선운동을 구현하기 위한 수학적인 해를 조사하였다.
2. 마모시험방법
2.1 Pin-on-disk 시험방법
일반적으로 암반굴착장비는 절삭성능을 최적화하도록 절삭공구들이 특정 간격으로 커터헤드에 배열되어 있다. 해당 간격은 회전굴착시 암반의 절삭특성 및 절삭조건(절삭깊이, 절삭각도 등)에 따라 결정되는 설계인자로서 로드헤더의 경우 절삭깊이대 간격의 비율이 1~5의 값을 가지며, TBM은 7~15 내외의 범위를 가지는 것으로 알려져 있다. 따라서 굴착장비의 실제 절삭간격을 모사할 수 있어야 실제 굴착환경과 동일한 조건으로 마모시험을 수행할 수 있다.
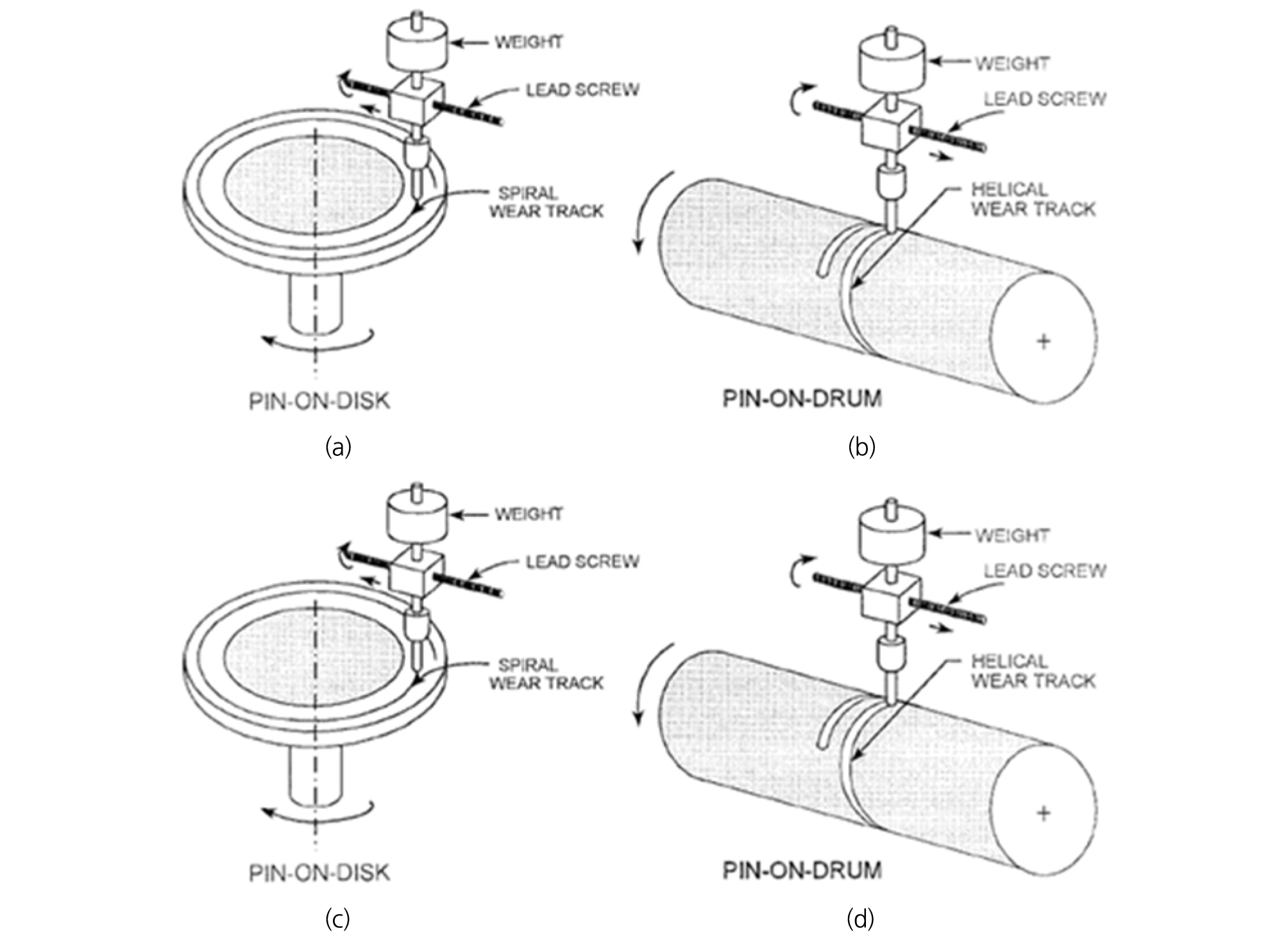
Fig. 1은 ASTM에서 제안한 4가지 마모시험방법을 보여주고 있다(ASTM, 2016). 해당 시험방법은 주로 금속시편 대 금속모재의 마모시험용으로 사용되는 방법이다. Fig. 1의 4가지 방법 중 암석재료를 모재로 사용하며 앞서 설명한 일정한 절삭간격을 모사할 수 있는 방법은 pin-on-disk(Fig.1(a))와 pin-on-drum(Fig.1(b)) 방식의 2가지이다. 이 중 전자의 경우 원판형 평면위에 나선운동을 모사하는 방식으로서 마모시험과 절삭성능시험에 모두 활용될 수 있는 방법이다. 따라서 본 연구에서 pin-on-disk 시험방식에 대해서 적합한 나선운동 방법을 분석하였다.
2.2 등간격 나선
나선은 여러 가지 형태의 함수로 표현할 수 있는데, 일정한 간격을 가지는 대표적 나선함수는 아르키메데스 나선이다. 이 나선의 함수는 극좌표계에서 식 (1)로 표현된다.
| $$r=a+b\theta\\(where,\;\;x=r\cos\theta,\;\;y=r\sin\theta)$$ | (1) |
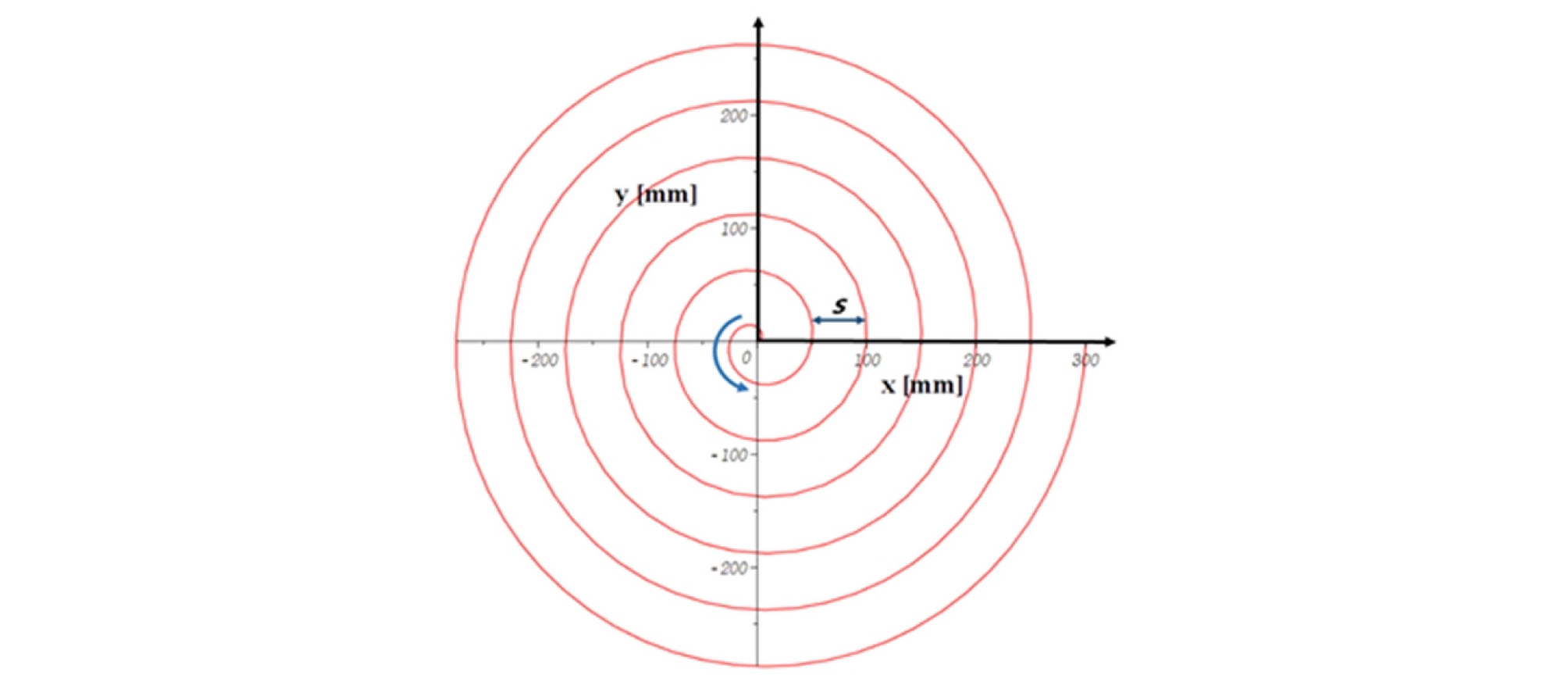
여기서, a는 나선의 시작점을 결정하는 상수이고, b는 인접한 나선의 간격에 영향을 미치는 상수이다. Fig. 2에 일정한 간격(s)을 가지는 아르키메데스 나선의 한 사례를 나타내었다.
3. 아르키메데스 나선 등속도 운동
3.1 등속도 방정식
일반적인 암반굴착에 사용되는 절삭공구는 각자 고유의 절삭속도를 가지도록 설계된다. 특정 절삭공구의 마모현상을 정확히 구현하기 위해서 Fig. 2의 아르키메데스 나선 궤적 위를 등속도로 운동하도록 제어해야 한다. 등속도 계산을 위해서 먼저 나선의 구간별 길이를 계산해야 한다. 어떤 곡선이 x=f(t), y=g(t)로 정의될 때, 특정구간(a ≤ t ≤ b)에서의 나선 길이(L)를 계산식은 아래 식 (2)와 같다.
| $$L=\int_{\;\;a}^b\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt=\int_{\;\;a}^b\sqrt{f'\left(t\right)^2+g'\left(t\right)^2}dt$$ | (2) |
직교좌표계(Cartesian coordinate system)에서 나선 위의 임의의 한 점의 좌표는 (x, y) = (r(t)·cos(θ(t)), r(t)·sin(θ(t)))로 표현된다. 해당 좌표를 식 (2)에 대입하면 식 (3)과 같은 나선길이에 대한 계산식을 얻는다.
상기 식 (3)을 나선의 이동시간(ts)에 대해 미분하면 식 (4)와 같이 나선의 속도에 대한 식이 도출된다. 이 식이 특정상수로 일정하게 유지될 때 나선운동은 등속도 운동을 만족하게 된다.
등속도 미분방정식, 식 (4)가 상수 c값을 가지도록 하는 나선 반경 (r(t))과 각도 (θ(t))를 구하면, 아르키메데스 나선 등속도 운동을 표현하기 위한 반경속도와 회전속도를 식으로 표현할 수 있다. 하지만, t에 대한 삼각함수가 많이 포함되어 있어서 역계산으로는 정확한 해를 구할 수 없다. 또한 수학계산 프로그램(Maple)을 통해서 시도해 봤지만 도출할 수 없었다. 관련 문헌을 검색했지만, 해당 방정식의 정해(exact solution)를 구한 문헌은 현재까지 검색되지 않았다.
3.2 나선 등속도 근사해 조사
한편 원자력 현미경(AFM, Atomic Force Microscopy)과 주사형 투과전자 현미경(STEM, Scanning Transmission Electron Microscopy) 분야에서 아르키메데스 나선을 등속도(Constant Linear Velocity, CLV)로 움직이기 위한 방법을 연구한 바 있다(Mahmood and Moheimani, 2010, Ziegler et al., 2016, Sang et al., 2017). 해당 연구는 현미경의 스캐닝 퀄리티를 높이기 위해 등속도 나선경로로 스캐닝해야 하는데, 이 때 등속도 아르키메데스 나선 운동에 대한 수학적 근사해를 제시하였다. 본 연구의 절삭공구의 등속도 운동과 연구목적은 다르지만 결과적으로 같은 접근방법을 가지므로 해당 방법을 소개하고 마모시험에 적용하고자 한다.
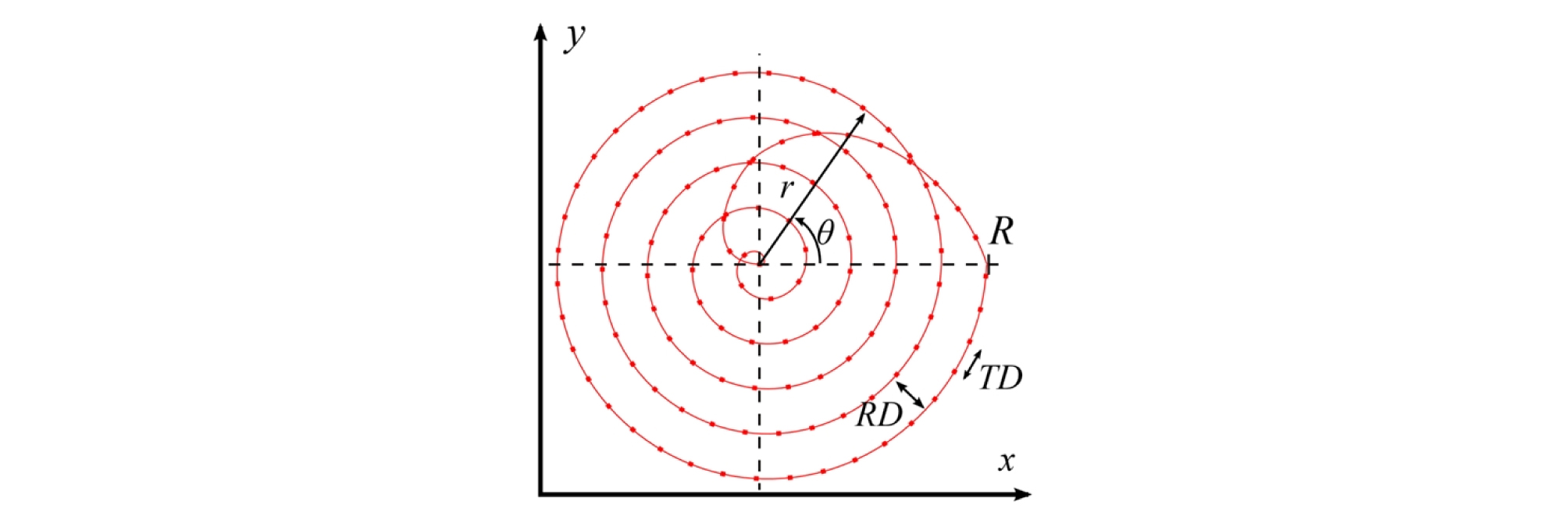
Zielger(2016)는 원의 안쪽에서 바깥쪽으로 이동하는 외향형 나선경로(Outward path)에서, 나선 반경(r)과 회전각도(θ)를 극좌표계에서 식 (5-6)과 같이 정의하였다 (Fig. 3).
| $$r=Rf(t_\ast)$$ | (5) |
| $$\theta=2\pi\;Nf(t_\ast)$$ | (6) |
여기서, R은 나선종료지점의 반경, N은 나선 수, t*는 t* = t/T 무차원 수, T는 나선 경로를 움직이는 전체 시간을 의미한다. f(t*)는 f(0)=0, f(1)=1을 만족하는 임의의 함수이다. 이 함수를 가정하고 선택하는 과정이 근사해를 구하는 핵심 과정이다.
식 (6)을 t*에 대해 미분하여 아르키메데스 나선 위를 움직이는 속도 (vs)를 식 (7)과 같이 나타낼 수 있다.
| $$v_L(t_\ast)=\frac{Rf'(t_\ast)}T\sqrt{(2\pi Nf{(t_\ast))}^2+1}$$ | (7) |
식 (7)이 상수가 되는 f(t*)를 미분방정식 계산을 통해 정확한 해를 찾는 것이 불가능하므로, 근사해를 찾아야 한다. 관련 문헌(Ziegler et al., 2016)에서는 f(t*)=로 제시하고 있으며, 이를 식 (7)에 적용하면 아래와 같이 나선 위를 움직이는 속도(vL)를 식 (8)과 같이 근사할 수 있다. 식 (8)에서 알 수 있듯이 나선 위를 움직이는 속도(vL)는 상수로 근사하여 표현 가능하다.
| $$v_L(t_\ast)=\frac{Rf'(t_\ast)}T\sqrt{(2\pi Nf{(t_\ast))}^2+1}\approx\frac{\pi NR}T$$ | (8) |
| $$\sqrt{(2\pi Nf{(t_\ast))}^2+1}=c\frac T{Rf'(t_\ast)}$$ | (9) |
식 (7)을 식 (8)로 근사하는 기존 문헌의 가정 및 계산방법(Ziegler et al., 2016)은 다음의 과정으로 요약할 수 있다.
① 식 (7)을 상수 c(vL=c)로 두고 식을 전개하면 식 (9)를 얻을 수 있다.
② 식 (9)의 미분방정식의 정확한 해를 구할 수 없는 이유는 좌측(left hand side)의 루트(root) 내에 있는 ‘+1’ 항 때문이며, ‘+1’ 항을 제거하여 근사하면, f(t*)=이라는 해가 도출된다.
③ 식 (9)로부터 알 수 있듯이 ‘+1’항 앞에는 2π, N, f(t*)가 곱해져 제곱된 항이 존재하는데, t*이 0에서 조금만 멀어지면 f(t*) 함수가 급속히 증가하므로, ‘+1“을 삭제해도 전체적으로 보면 비슷한 함수가 될 수 있다.
④ 따라서, 원점과 일정부분 떨어진 영역에 대해서 식 (8)을 식 (7)의 근사해로 사용할 수 있다.
3.3 고유 상수 및 속도성분
기존 문헌(Ziegler et al., 2016)에서 아르키메데스 나선의 등속도 운동을 정의하는 고유 상수는 R, T, N의 3개이다. 즉, 3개의 상수를 정의하면 1개의 아르키메데스 나선의 최대반경, 등속도, 등간격 3가지 요소가 결정된다. 절삭공구의 마모시험에서는 상기 고유인자보다 시험편 최대반경(Rs), 나선의 속도(vs), 나선의 간격(s) 3가지 성분이 핵심 시험인자이다. 최대반경과 속도는 기존 수식과 동일하고, 나선간격만 정리하면 된다. 기존 인자와 신규 인자의 관계는 식 (10)과 같다.
| $$R=R_s,\;\;v_s=v_L=\frac{\pi NR}T,\;\;\;s=\frac RN$$ | (10) |
또한, 아르키메데스 나선을 등속도로 제어하기 위해 반경방향 속도와 회전속도 2가지 독립적인 벡터 성분을 제어해야 한다. 반경방향 속도와 회전속도는 식 (5)와 (6)을 각각 시간(t*)에 대해 미분하여 구한다. 그 결과는 식 (11), (12)와 같다. 회전속도 식에서 편의를 위해 radian 단위와 RPM 단위를 동시에 나타내었다.
| $$\frac d{dt}\theta(t_\ast)=\frac RTf'(t_\ast)=\frac R{2T}{(t_\ast)}^{-\frac12}$$ | (11) |
| $$\frac d{dt}\theta(t_\ast)=\frac{2\pi N}Tf'(t_\ast)\;\lbrack rad/s\rbrack=\frac{\pi N}T{(t_\ast)}^{-\frac12}・\frac{60}{2\pi}\lbrack RPM\rbrack$$ | (12) |
4. 나선 등속도 계산예시
4.1 외향형 나선
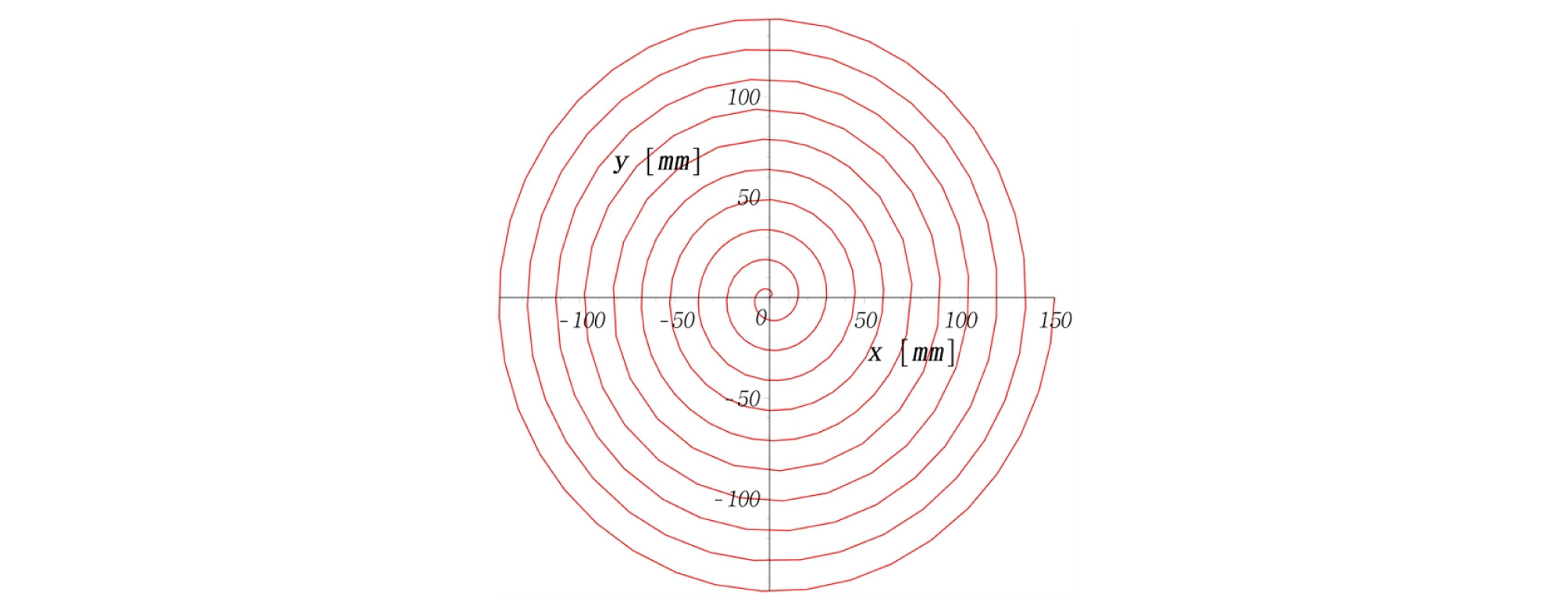
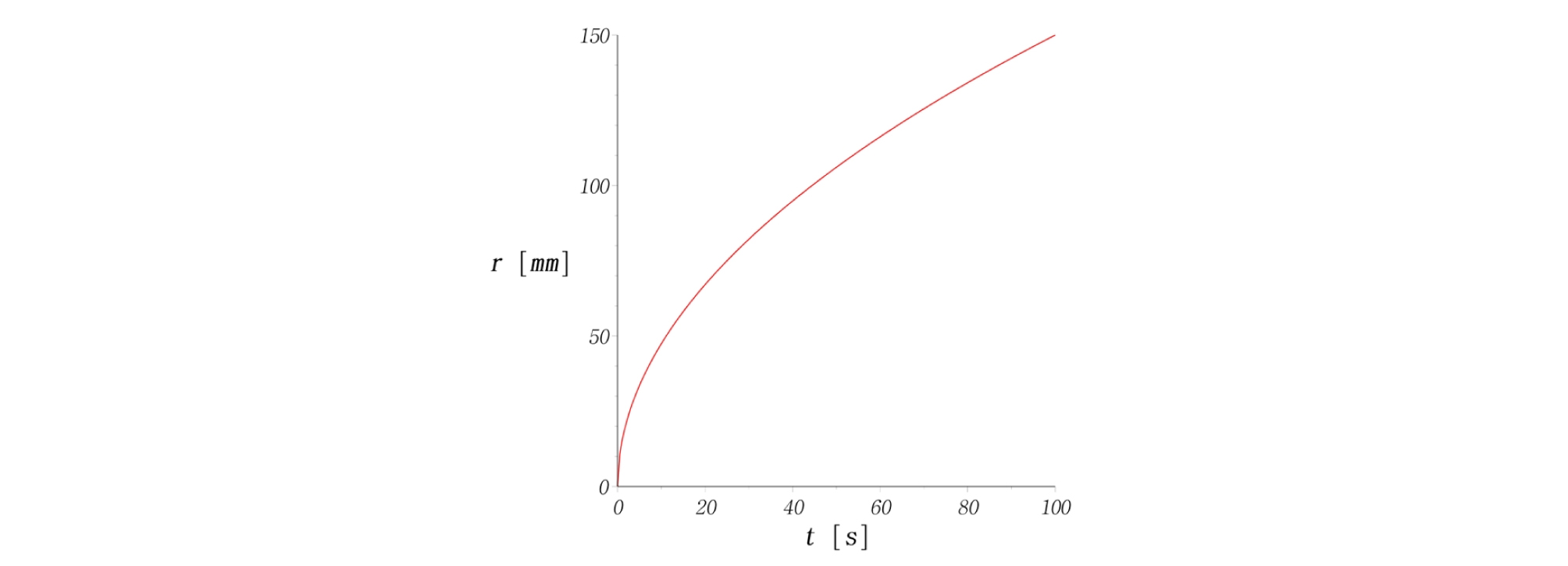
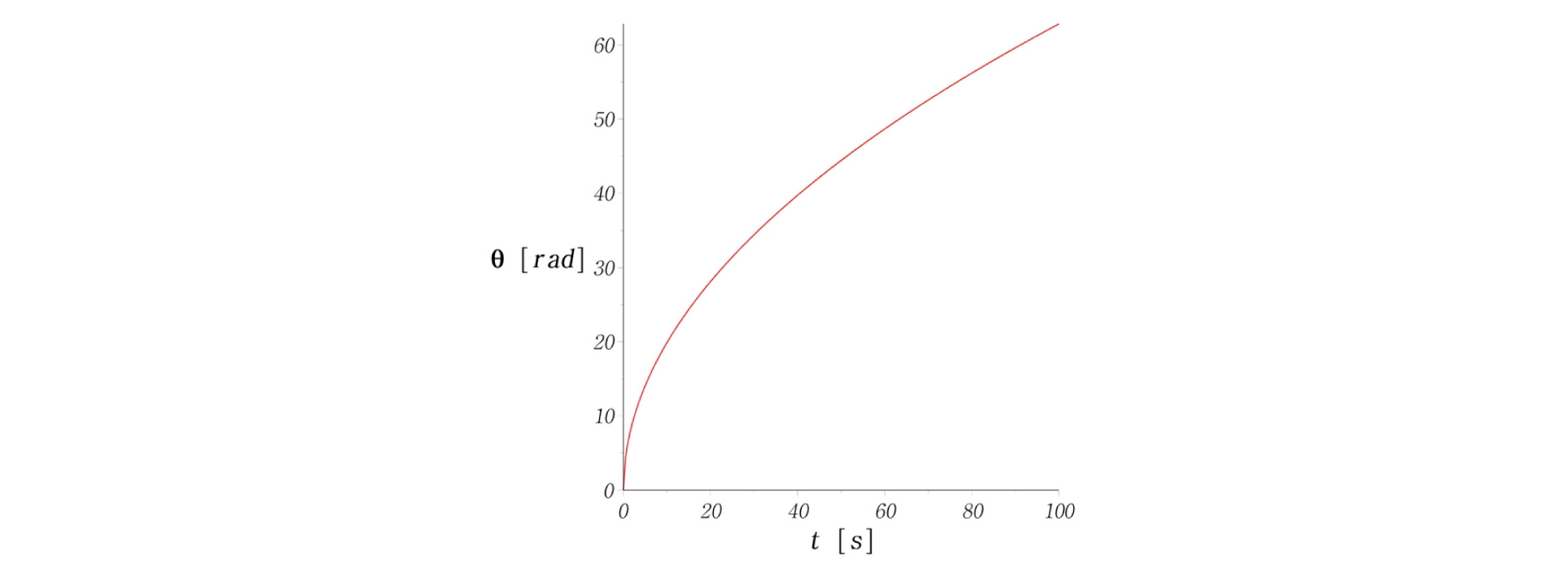
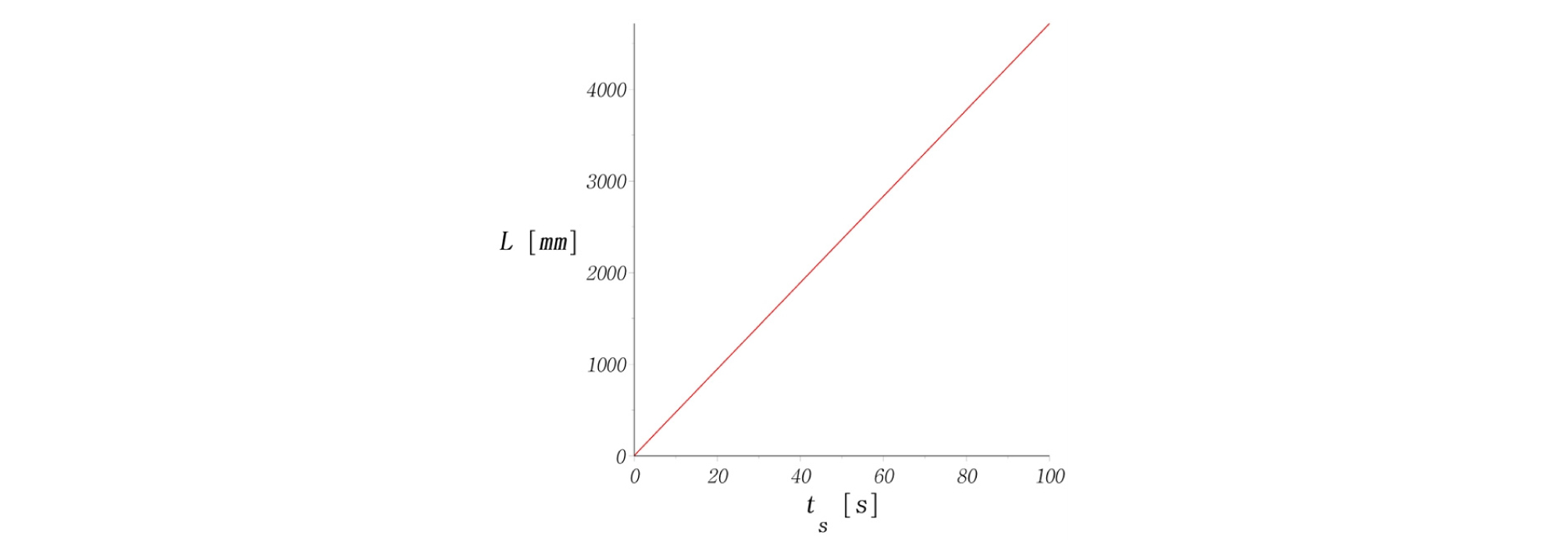
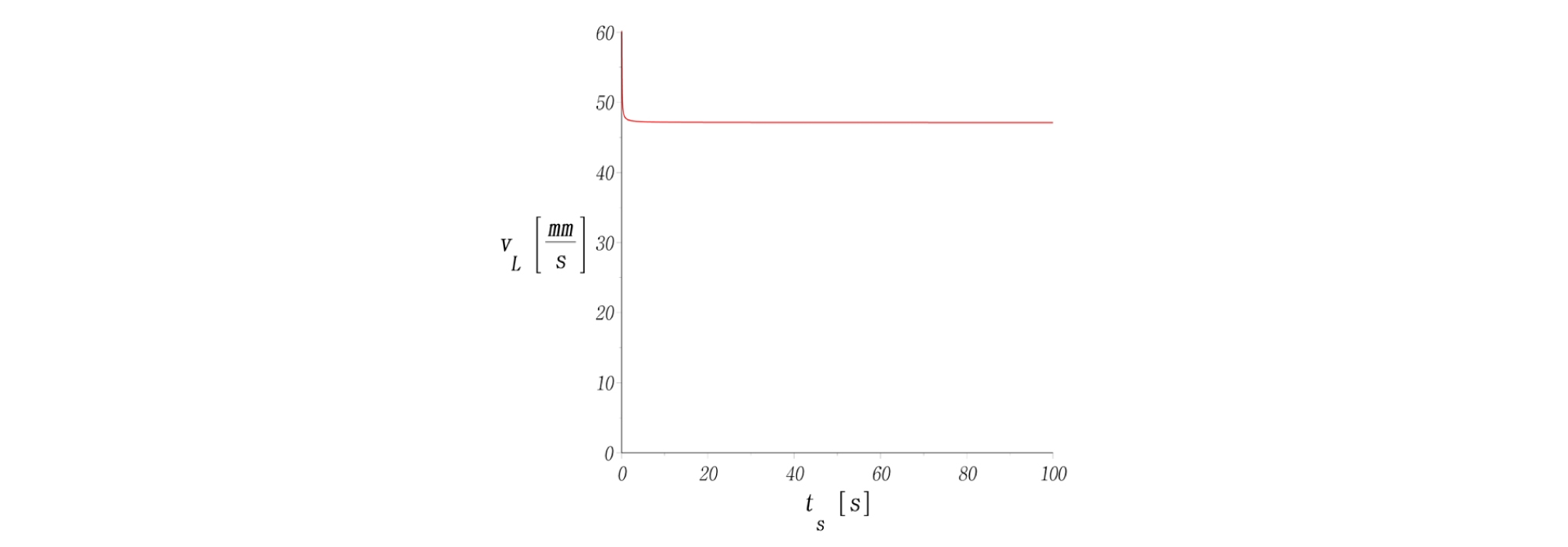
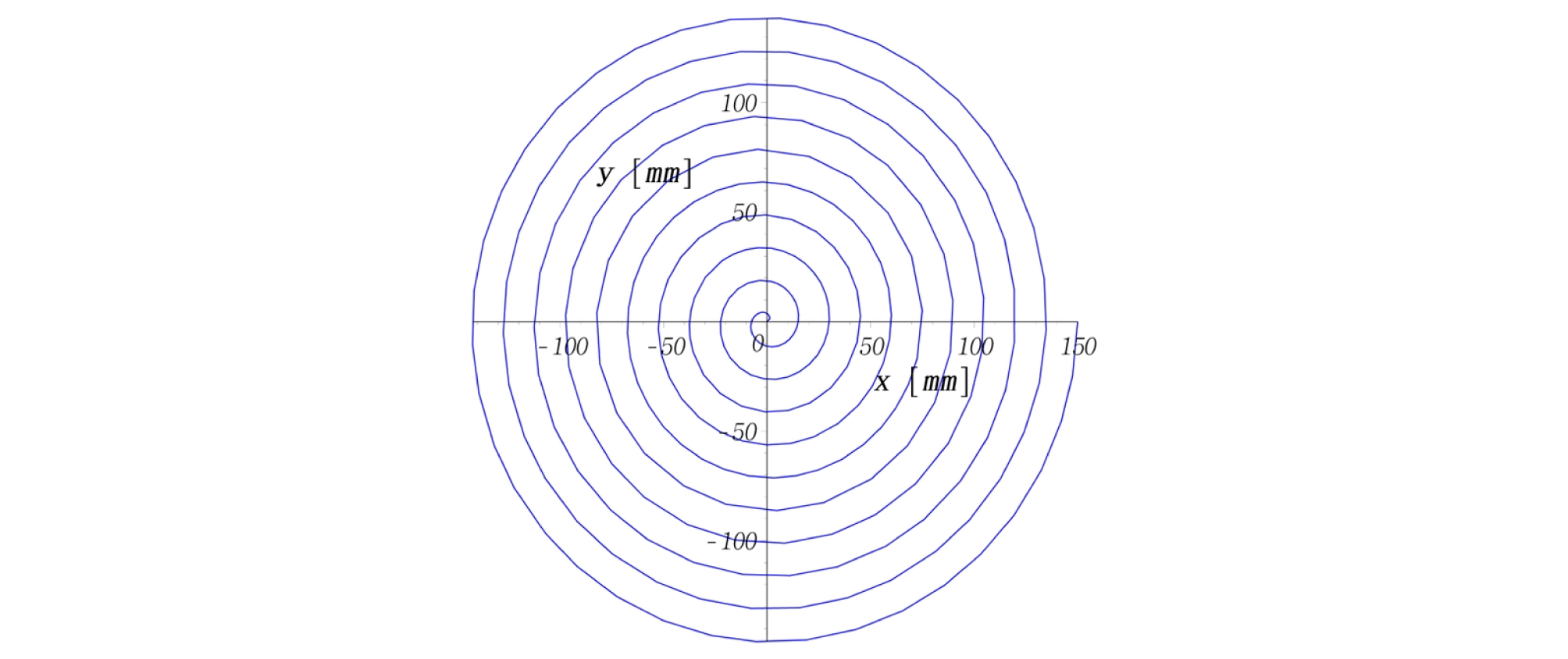
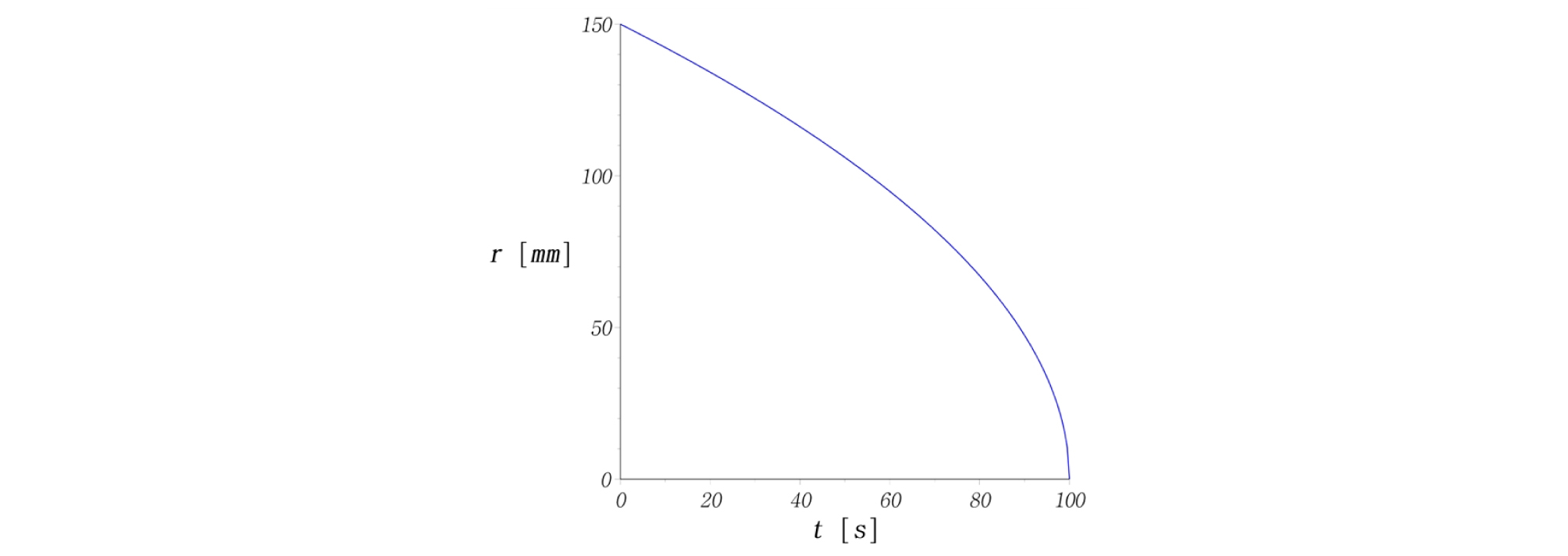
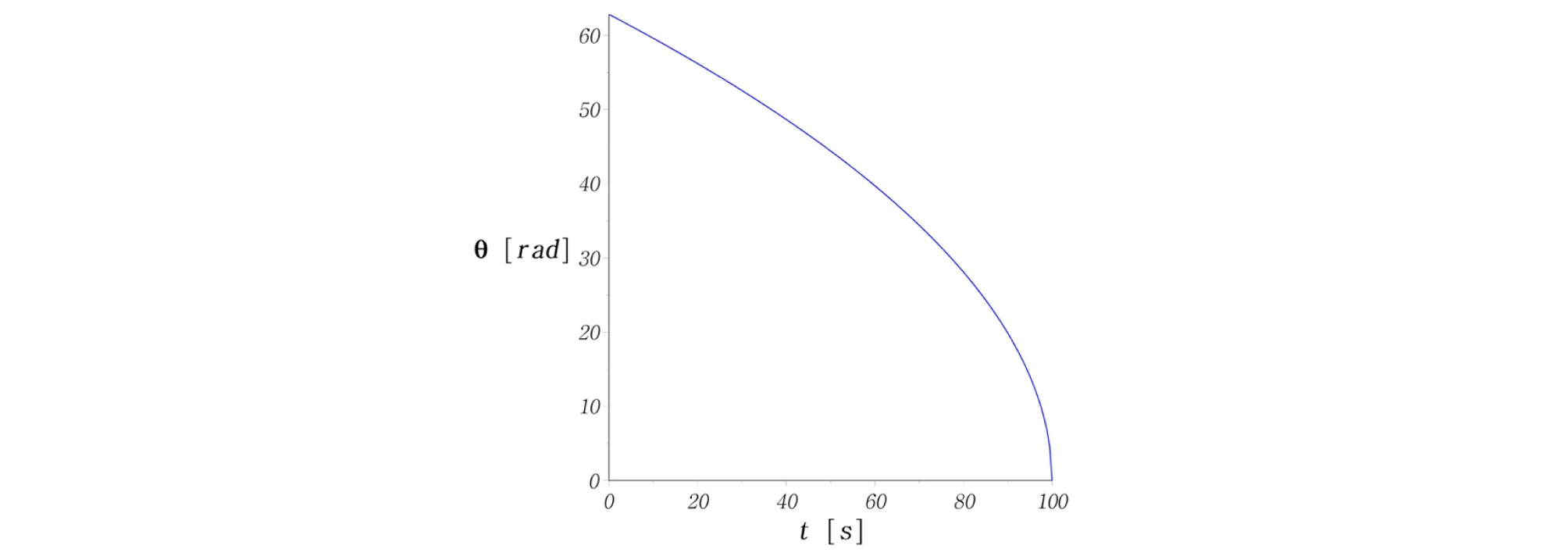
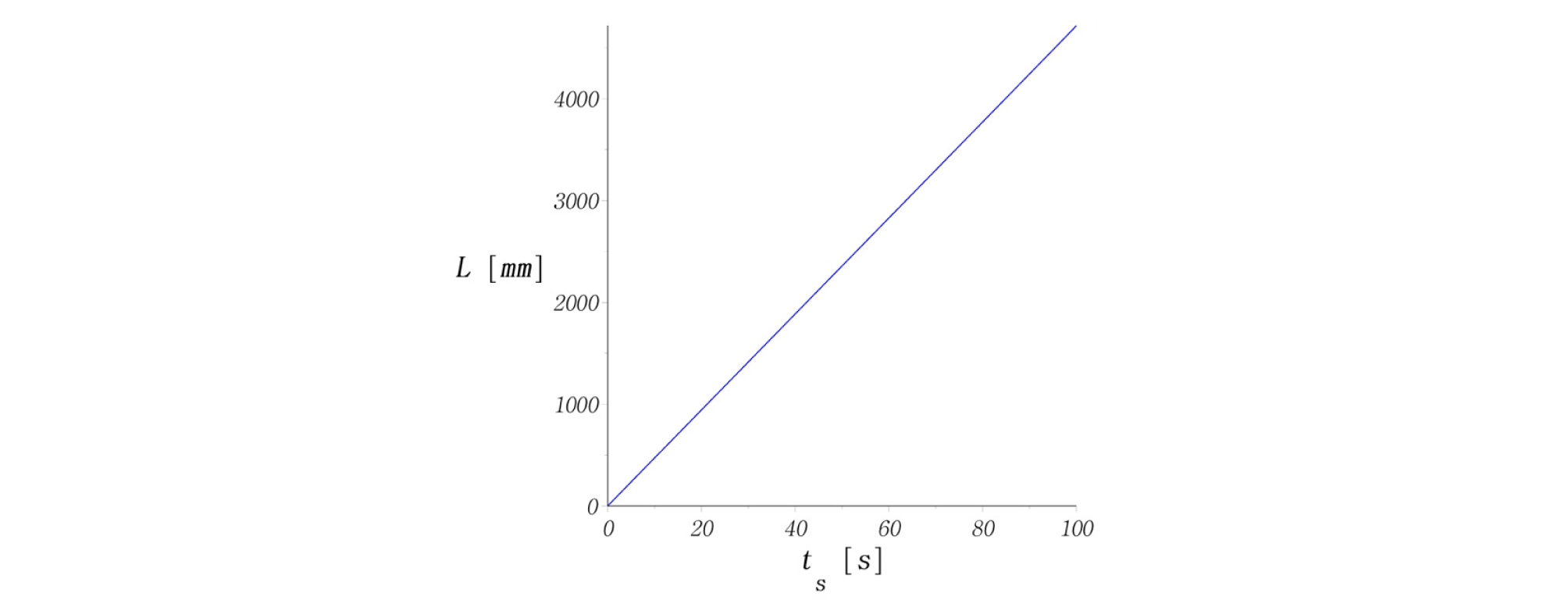
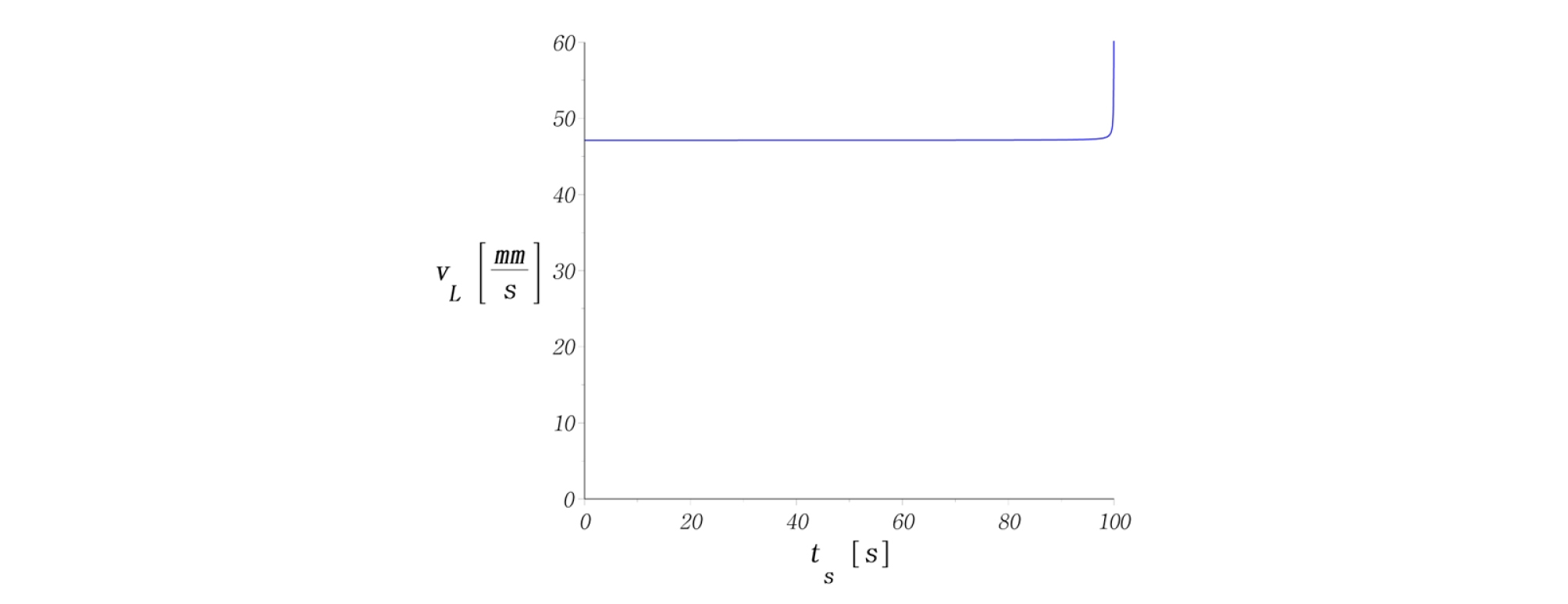
외향형 나선(outward spiral)을 적용하면, Fig. 4와 같이 원통형 시편의 중심부로부터 외각방향으로 나가면서 시험이 진행된다. 이 때 고유상수 3개를 Table 1과 같이 결정하여 나선경로, 나선반경(r), 회전각도(θ), 길이변화, 속도변화를 계산해 보았다(Figs. 5-9). Figs. 6-7을 보면 반경과 각도가 비선형적으로 증가하는 것을 알 수 있다. 따라서 2가지 벡터성분인, 반경속도와 회전속도가 동시에 제어되어야만 등속도 운동을 구현할 수 있다는 것을 보여준다. 즉, 위의 수식을 사용할 때, 2가지 성분 중 1가지만 변화해서는 등속도 운동을 만족할 수 없다.
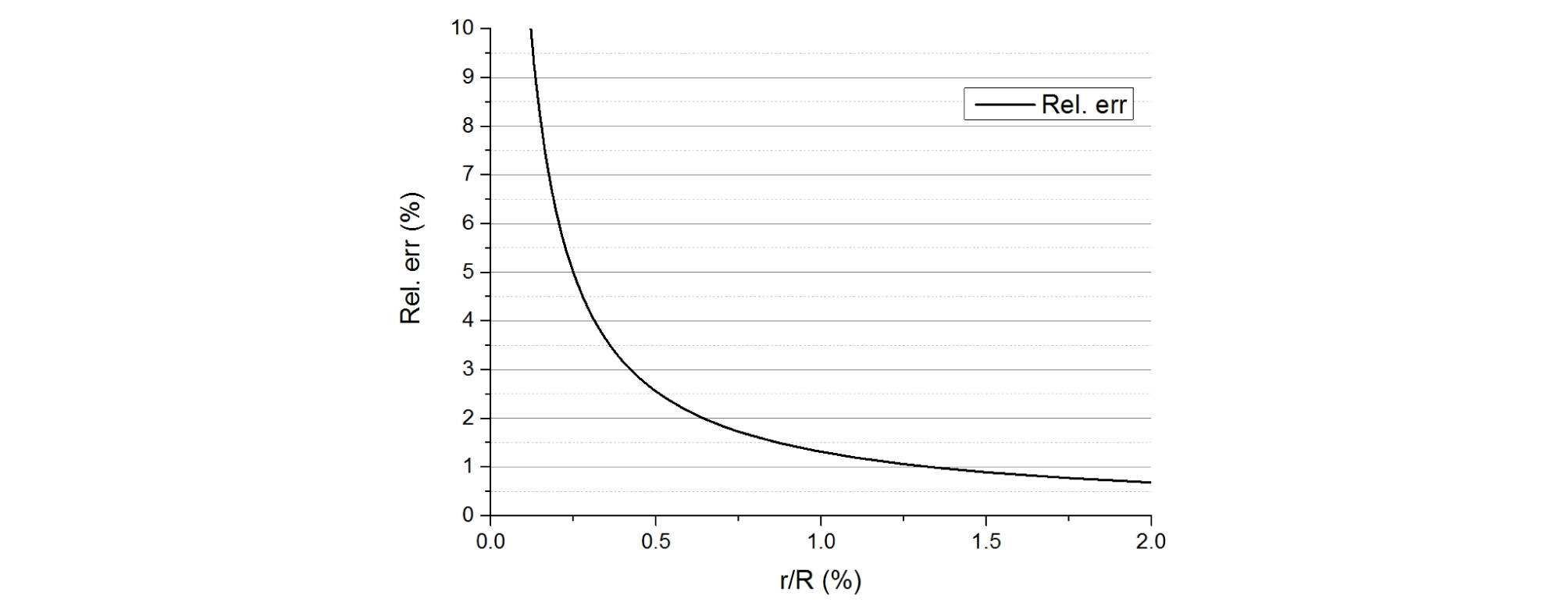
Fig. 9를 보면 등속도를 만족하지 않는 영역이 원점(시작점)에 인접한 국소영역에서 발생하는 것을 알 수 있다. 원점 부근을 확대하여 상대오차를 표현하면 Fig. 10과 같다. 여기서 최대반경의 0.1%인 1.5 mm를 지나면 상대오차(relative error) 값이 1.25% 이내로 수렴한다. 등속도운행시 원점에 근접할수록 RPM은 기하급수적으로 증가하여 일반적으로 사용되는 모터의 한계속도를 초과하는 영역이 발생한다. 그래서 나선의 원점 인접한 영역은 장비의 RPM 한계로 인해 접근할 수 없다. 최대반경(R)의 1.5%지점인 0.015R지점에서 나선을 출발시키면 1.0% 이내의 오차로 등속도를 만족한다. 따라서 기존 문헌(Ziegler et al., 2016)에서 제안한 근사해(식 (8))는 원점 오프셋(offset)을 설정하면, 실제 시험장비에서 구현하기에 문제가 없을 것으로 판단된다.
4.2 내향형 나선
내향형 나선(inward spiral)은 Fig. 11과 같이 시편 밖에서부터 중심부로 들어오면서 시험하는 경로를 가진다. 외향형 나선 경로(outward spiral path)에서 시간을 반대로 돌리면 내향형 나선 경로가 된다. 간단히 수식으로 나타내면, f(t*)=를 y축을 기준으로 대칭하고 +x축으로 T만큼 이동하는 과정으로 식 (13)과 같다.
| $$f(t_\ast)=\sqrt{\frac{-(t-T)}T}=\sqrt{-\frac tT+1}=\sqrt{-t_\ast+1}$$ | (13) |
즉, 내향형 나선의 수식은 식 (5-6)에 f(t*)=을 적용하면 된다.
상기 외향형 나선의 상수와 같은 조건(Table 1)에서 내향형 나선의 경로, 나선반경(r), 회전각도(θ), 길이변화, 속도변화를 계산하면 Figs. 12~16과 같고, 내향형 나선 그래프에 비해 y축에 대칭되는 형태를 가진다. 그리고 내향형 나선의 속도오차도 원점부근에서 발생하는데, 외향형과 반대이므로 시험종료 지점에 해당한다(Fig. 16). 이 역시 시험의 종료구간을 원점에서 특정 값 이상 벗어나도록 원점 오프셋을 설정하면 오차수준을 1%이하로 제어할 수 있다.
5. 결 론
암석 절삭공구의 마모시험을 pin-on-disk 방식으로 수행하려면 아르키메데스 나선 등속도 운동을 만족해야 한다. 본 연구는 해당 방법을 구현하기 위해 수학적 근사해와 마모시험에 적용하는 방법을 조사하였다.
1) 원자력 현미경, 전자현미경 분야에서 아르키메데스 나선의 등속도 운동조건을 이미 연구하였으므로, 기존 연구의 수학적 근사해를 인용하여 소개하였다. 근사해를 이용한 외향형 나선과 내향형 나선의 등속도 운동 방정식을 제시하였다. 이 때, 아르키메데스 등속도 나선함수는 3개의 고유상수를 가진다.
2) 암석공구 내구시험 조건에 적용하기 위해 특정 상수 조건에서 외향형, 내향형 아르키메데스 나선의 운동 경로, 길이변화, 속도변화를 계산하였다. 계산결과, 나선운동 경로는 등간격으로 거의 일정하였으며, 나선 속도는 원점 부근을 제외하고는 거의 등속도를 유지하였다.
3) 초기 시간 에서 오차가 큰 이유는 근사하는 과정에서 식 (7)의 제곱근 안에 있는 ‘+1’ 항을 생략하여 나선 진행시간(ts)이 0에 가까울수록 무시했던 ‘+1’ 항의 영향이 커지기 때문이다. 전체 나선 움직임 중 초기시간 또는 종료시간에 대한 부분을 원점 오프셋으로 설정하면 이러한 오차를 줄일 수 있다. 즉, 원점에서 0.015R이상의 오프셋을 설정하면 오차를 1% 이내로 유지할 수 있다.
기존 연구에서 제시한 근사해를 이용한 등속도 제어방법은 향후 암석공구의 마모시험 방법으로 사용할 수 있을 것으로 판단된다. 향후 오프셋을 추가 변수로 설정시 아르키메데스 나선함수의 방정식 및 고유상수를 추가적으로 조사할 예정이다.