1. 서 론
2. 1차원 기체 주입 시험 소개(DECOVALEX-2019 Task A: Stage 1A)
2.1 DECOVALEX-2019 Task A 소개
2.2 1차원 기체 주입 시험(Stage 1A)
3. 수치해석 모델
3.1 다공성 매질에서의 2상 유동
3.2 유효응력 개념을 고려한 역학 손상 모델
3.3 손상도에 따른 수리 물성 변화
3.4 해석 모델
3.5 모델링 스케쥴
4. 해석 결과
4.1
4.2
5. 결 론
1. 서 론
지하 심부에 고준위방사성폐기물을 처분하는 심지층 처분시스템에서는 공학적방벽(Engineered Barrier System, EBS)과 천연 방벽(Natural Barrier System, NBS)으로 이루어진 다중 방벽 시스템을 통해 방사성 물질의 누출을 방지한다(IAEA, 2011). 이 중 처분 용기와 벤토나이트 완충재로 구성된 공학적 방벽의 경우, 처분장 폐쇄 후 최소 몇백 년 이상 주변 암반으로의 방사성 핵종 누출을 억제해야 하므로 장기 건전성 확보가 필수적이다(NEA-EC, 2003).
공학적 방벽 내, 특히 처분 용기와 벤토나이트 완충재 사이 경계 부근에서는 처분 용기의 부식이나 고준위방폐물의 방사성 붕괴, 방사선에 의한 지하수 분해 등 다양한 원인으로 인해 기체가 발생하게 된다(Cuss et al., 2014, Ahusborde et al., 2015, Shaw, 2015). 이렇게 발생한 기체는 벤토나이트 완충재의 높은 포화도 및 낮은 투수율로 인해 점진적으로 쌓이게 되어 기체 압력 증가 현상이 발생하는데(Weetjens and Sillen, 2006, Ortiz et al., 2002, Wikramaratna et al., 1993), 기체의 압력이 기체 유입 압력(gas entry pressure)을 넘어서게 되면 기체가 급격히 벤토나이트 완충재로 들어가게 되는 기체 이동 현상(gas migration)이 발생하게 된다(Horseman, 1996, Horseman et al., 1997, Horseman et al., 1999). 만약 기체상 방사성 핵종이 발생하였을 경우 앞서 설명한 기체 이동 현상에 의해 주변 암반으로 급격하게 누출될 수 있기에, 공학적 방벽의 장기 건전성 확보 측면에서 기체 이동 현상을 명확히 규명하는 것이 매우 중요하다.
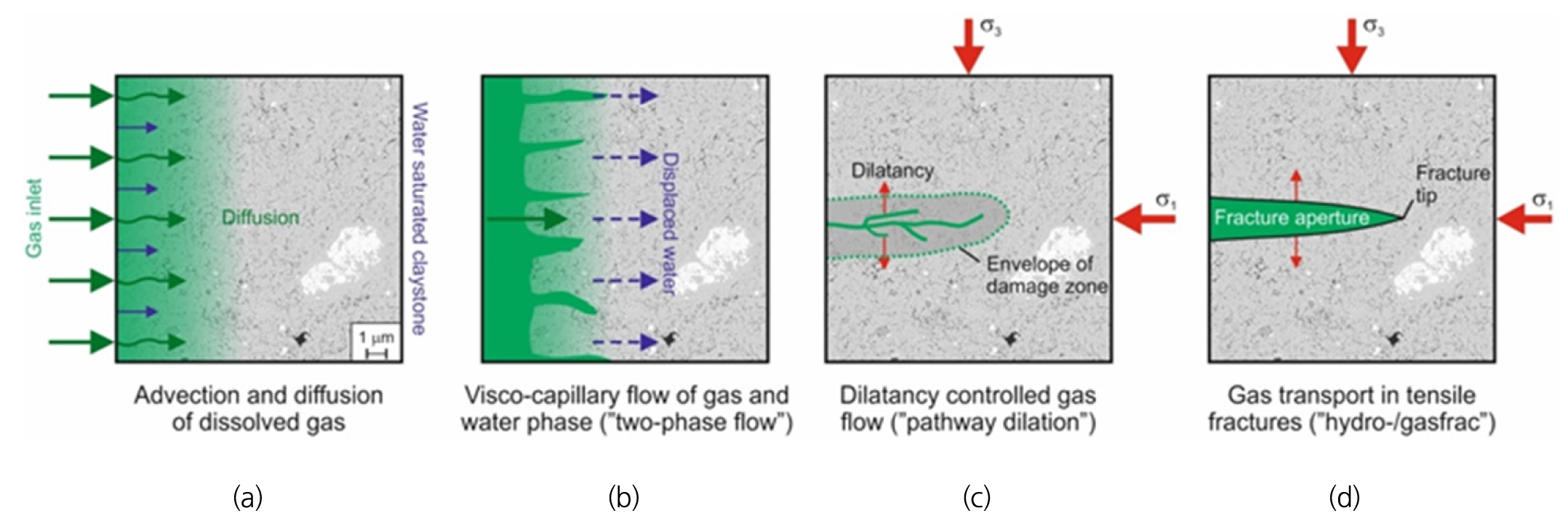
벤토나이트 완충재와 같이 점토 물질을 다량 함유한 매질에서의 기체 이동 현상은 Fig. 1과 같이 4가지 주요 메커니즘으로 나타낼 수 있으며 이는 다음과 같다(Cuss et al., 2014, Marschall et al., 2005): (a) 공극수에 용해된 기체의 이류 및 확산; (b) 점성-모세관(visco-capillary) 2상 유동; (c) 기체 압력에 의해 매질 입자 사이가 벌어지면서 발생하는 팽창 흐름(dilation flow); 마지막으로 (d) 기체 압력에 의한 거시적인 인장 절리를 따라 발생하는 기체 흐름이다.
첫 번째 메커니즘인 공극수에 용해된 기체의 이류-확산 이동은, 생성된 기체 분자가 공극수에 용해되어 액체의 흐름에 따라 이동하거나(이류) 용해된 기체 분자의 농도차로 인해 이동하는 현상(확산)을 의미한다. 이 중, 이류는 압력 구배에 의한 유체 유동을 나타내는 Darcy의 법칙을 따르며, 확산은 공극수의 기체 농도 구배에 의한 유체 유동을 나타내는 Fick의 법칙 및 공극수에 용해되는 정도를 나타내는 Henry의 법칙을 따른다.
두 번째 메커니즘인 점성-모세관 2상 유동은, 불포화 매질에서 점성 및 모세관압의 영향으로 매질의 공극에서 공극수가 기체로 대체되는 이동 현상을 의미한다. 이는 전통적인 2상 유동 모델에 해당하며, 기체는 고유 투수율(intrinsic permeability), 투수율(permeability)과 포화도(saturation)의 관계(상대 투수율(relative permeability)) 및 모세관압(capillary pressure)과 포화도의 관계(흡입력(suction) 또는 수분 보유 곡선(water retention curve))를 따라 이동한다. 또한 기체가 매질의 공극으로 들어가기 위해 필요한 최소 흡인력인 공기 유입 값(air-entry value, AEV) 또는 기체 유입 압력은 점성-모세관 2상 유동 메커니즘에 있어서 중요한 인자이며, 가장 큰 공극을 통해 기체 및 유체가 유입되기 때문에 매질의 최대 공극 크기와 매우 밀접한 관련이 있다.
기준 레벨 이상의 기체 압력 하에서의 기체 흐름은 우선 경로(preferential pathway)의 생성 및 매질의 팽창에 의해 발생하는데, Marschall et al. (2005)은 이 기체 이동 현상을 팽창 제어 기체 흐름(dilatancy-controlled gas flow) 또는 ‘통로 팽창(pathway dilation)’으로 설명하였으며, 이 현상이 벤토나이트 완충재와 같이 점토 물질을 다량 함유한 매질에서만 나타나는 매우 중요한 기체 흐름 현상임을 확인하였다. 기체 압력이 기준 응력 수준을 넘어설 때 매질 입자 사이가 기체 압력에 의해 벌어지면서 매질의 팽창이 발생하며, 이러한 변형(deformation)에 의해 미세 균열(microfracture)이 형성된다(Davis and Selvadurai, 2002). 이러한 미세 균열의 발생은 공극의 크기를 변화시킴으로써 매질의 고유 투수율을 증가시킴과 동시에 모세관압과 포화도의 관계를 나타내는 수분 보유 곡선을 변화시킨다. 즉, 매질의 응력 상태와 변형 정도에 따라 미세 균열 발생 및 기체 이동 양상이 달라지기 때문에, 세 번째 메커니즘인 팽창 흐름을 모사하기 위해서는 매질의 수리-역학적 상호작용(coupled hydro-mechanical behavior)을 고려한 해석이 필수적이다.
마지막으로 네 번째 메커니즘은 저류층 수리 자극(reservoir stimulation)에서 관찰되는 현상과 유사하게 기체의 압력에 의해 거시적인 인장 절리가 생성되고, 이 절리를 따라 기체 흐름이 발생하는 현상이다. 이는 앞서 설명한 미세 균열에 의한 팽창 흐름과는 다르게 기체 생성 및 축적이 빠르고 기체 압력이 최소 주응력과 인장 강도의 합보다 큰 경우 발생하게 된다.
공학적 방벽에서의 기체 이동 현상은 이처럼 복잡한 메커니즘들에 의해 발생하기 때문에, 수치 모델링 화 하는 데 있어 기존의 전통적인 2상 유동 개념만으로는 이 현상을 명확히 모사할 수 없다(Horseman et al., 1996, 2004, Harrington and Horseman, 1999, Angeli et al., 2009, Harrington et al., 2009, 2012). 따라서 이를 해결하기 위해 다양한 수치 해석적 시도들이 행해져왔지만(Nash et al., 1998, Hoch et al., 2004, Fall et al., 2014, Nguyen and Le, 2015), 무작위적인 우선 경로 생성과 같은 불확실성들로 인해 적합한 기체 이동 모델을 구성하는 데 문제가 발생하였다. 또한 공학적 방벽에서의 기체 이동 메커니즘, 특히 기체 압력에 의해 매질 입자 사이가 벌어지면서 발생하는 팽창 흐름에 대한 불확실성도 아직 존재하기 때문에, 고준위방사성폐기물처분장의 장기 건전성을 평가하기 위해서는 새로운 수학적 모델 및 수치 모델 개발이 필수적이다.
벤토나이트 완충재와 같은 저투수율 매질에서의 기체 이동과 관련한 국제적인 관심사를 토대로 국제 공동 연구 프로젝트인 DEvelopment of COupled models and their VALidation against EXperiments-2019 (DECOVALEX-2019) Task A가 수립되었으며, 기체 압력에 의해 매질 입자 사이가 벌어지면서 발생하는 팽창 흐름을 적절하게 모델링하는 데 필요한 수리-역학적(HM) 메커니즘을 규명하고 정량적인 기체 이동 현상 모델 개발 및 검증이 수행되고 있다. 본 연구는 DECOVALEX-2019 Task A의 일환으로 수행되었으며, 그 일부인 Stage 1A에 해당하는 1차원 기체 주입 시험 모델링에 관한 연구이다. 본 논문에서는 공학적 방벽에서의 기체 이동 현상을 모사하고자 역학 손상 모델 및 손상도를 고려한 2상 유동 모델을 개발하였으며, 일정 체적 경계 조건(constant volume boundary condition) 하에서의 1차원 기체 주입 시험 모사를 통해 개발된 모델의 적용성을 검토하였다.
2. 1차원 기체 주입 시험 소개(DECOVALEX-2019 Task A: Stage 1A)
2.1 DECOVALEX-2019 Task A 소개
DECOVALEX-2019 Task A: modElliNg Gas INjection ExpERiments (ENGINEER)는 벤토나이트 및 점성토에서의 기체 이동 현상 모델링을 위해 영국 지질조사소(British Geological Survey(BGS))가 제안한 국제 공동 프로젝트이며, 벤토나이트 완충재를 포함한 공학적 방벽에서의 기체 이동 현상의 정량적 평가를 위한 새로운 수치 해석 기법 개발 및 검증이 주목적이다. 이 프로젝트에는 총 8개국의 9개 기관이 참여하고 있으며(Table 1), 1년에 2회 개최되는 워크숍을 통해 서로의 연구결과를 공유하고 의견을 교류함으로써 벤토나이트 및 점성토에서의 기체 이동 현상에 대한 수치해석 방법론 및 모델을 개발하고 있다. DECOVALEX-2019 Task A는 총 4개의 단계로 구성되어 있으며, 각 단계 특성에 따라 필수적으로 수행해야하는 과제와 선택적으로 수행하는 과제로 구성되어 있다(Table 2).
Table 1. Research teams of DECOVALEX-2019 Task A
Table 2. Stages of DECOVALEX-2019 Task A
2.2 1차원 기체 주입 시험(Stage 1A)
벤토나이트 완충재에서의 기체 이동 현상을 규명하고자 BGS에서는 일정 체적 경계 조건 하에서의 1차원 기체 주입 시험을 수행하였으며, 시험 장치 및 센서 개념도는 Fig. 2와 같다(Daniels and Harrington, 2017). 시험에 사용된 벤토나이트 시료는 MX-80을 이용하여 직경 60 mm 및 길이 120 mm 크기로 제작되었으며, 약 98 % 포화된 상태로 시험을 수행하였다. 약 120 일 간 한쪽 면에는 헬륨 기체를 주입하고 반대면에는 일정한 수압을 걸어줌으로써 1차원 기체 주입 시험을 수행하였으며, 공극 수압을 비롯하여 축방향 응력 및 기체 유출양을 측정함으로써 기체 이동 메커니즘을 규명하고자 하였다.
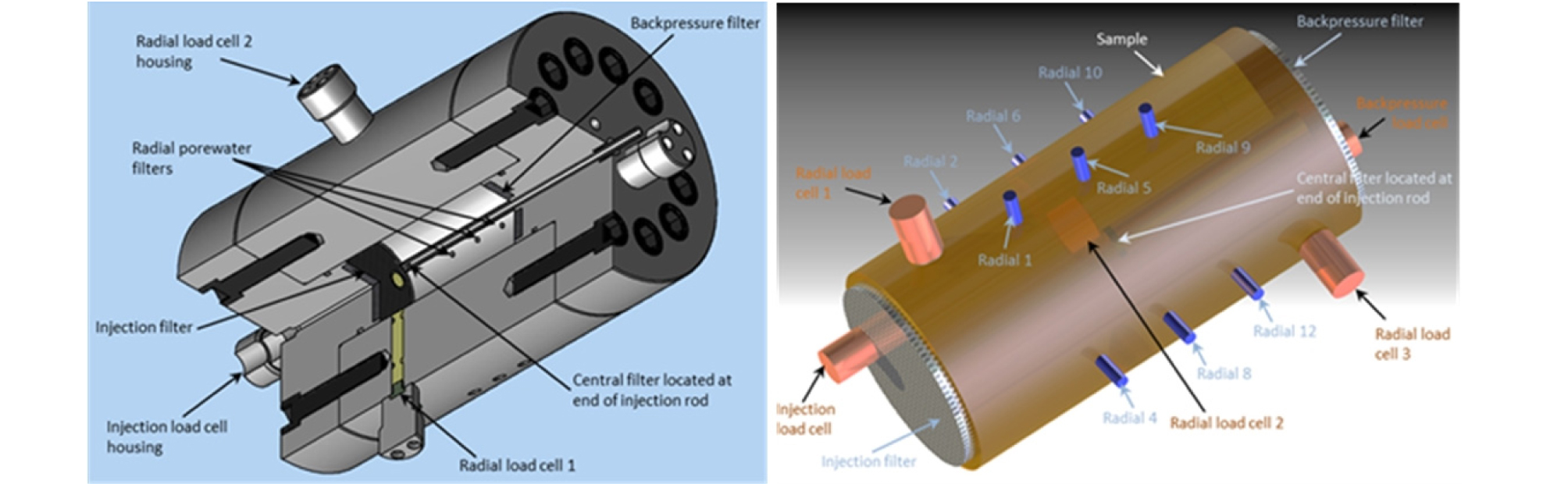
Fig. 2.
Cut-away diagram of the pressure vessel and image of the sample with the relative positions of the load cells and pore pressure filters (Daniels and Harrington, 2017)
3. 수치해석 모델
본 연구에서는 벤토나이트 완충재에서의 기체 이동 메커니즘 중 기체 압력에 의해 매질 입자 사이가 벌어지면서 발생하는 팽창 흐름을 모사하기 위해 수리-역학적 상호작용을 고려한 모델을 개발하였으며, 주요 지배방정식 및 구성방정식은 다음과 같다.
(1) 다공성 매질에서의 2상 유동
(2) 유효응력 개념을 고려한 역학 손상 모델
(3) 손상도에 따른 수리 물성 변화
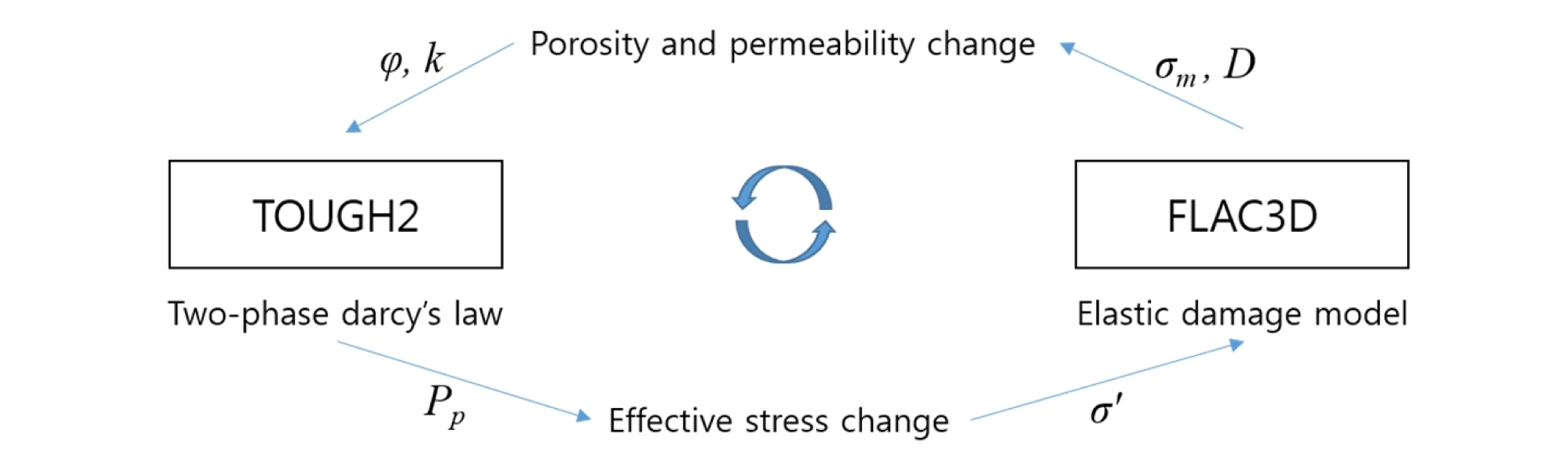
벤토나이트 완충재의 공극에서의 기체상 유동 및 액체상에 녹아있는 기체의 유동을 고려하기 위해 다공성 매질에서의 2상 유동을 고려하였다. 또한 기체 압력이 기준 응력 수준을 넘어설 때 매질 입자 사이가 기체 압력에 의해 벌어지면서 미세 균열의 형성 및 매질 팽창 현상이 발생하며, 이러한 미세 균열을 따라 기체가 갑작스럽게 이동하는 기체 이동 현상을 모사하기 위해 손상도 개념을 도입하였다. 기체 압력으로 인해 미세 균열의 형성 및 매질 팽창 정도를 손상도로 나타내었으며, 공극 수압의 변화로 인한 매질의 손상도(damage)를 판단하기 위해 유효응력 개념을 고려한 역학 손상 모델을 적용하였다. 마지막으로 손상도에 따른 수리 물성 변화를 고려함으로써 매질의 변형에 의한 기체의 팽창 흐름을 모사하였다. 개발된 모델의 적용성 검토를 위해 지반공학 및 암반공학 분야의 범용 수치해석 코드인 TOUGH-FLAC을 이용하였으며(Rutqvist et al., 2002), 일부 코드 수정을 통해 본 연구에서 개발된 모델을 적용하였다(Fig. 3).
먼저 TOUGH2에서는 전통적인 다공성 매질에서의 2상 유동 해석을 수행하였으며, 해석 결과인 공극 수압을 이용해 FLAC3D에서 유효응력을 변화시킨 후 역학 손상 모델을 이용하여 역학 해석을 수행하였다. FLAC3D 해석 결과인 평균 응력과 매질의 손상도를 바탕으로 수리 물성인 공극률과 투수율을 변화시켜 TOUGH2 해석을 다시 수행하였으며, 이 과정을 반복적으로 수행해 전체적인 해석을 진행하였다.
3.1 다공성 매질에서의 2상 유동
Vn의 부피를 갖고 Γn의 면적을 갖는 임의의 도메인에서의 질량 보존 방정식은 다음과 같다(Pruess et al., 1999).
| $$\frac d{dt}\int_{V_n}M^\kappa d\;V_n=\int_{\Gamma_n}\mathbf F^\kappa\cdot\mathbf nd\mathit\;\Gamma_{\mathit n}+\int_{{\mathrm V}_{\mathrm n}}q^{\mathit\kappa}d\mathit\;V_{\mathit n}$$ | (1) |
여기서 M은 단위 부피당 전체 질량(mass accumulation) [kg/m3], κ는 각각의 질량 성분(mass component), F는 단위 면적 당 질량 유속(mass flux) [kg/(m2·s)], q는 단위 부피당 유출 혹은 유입량(sink or source) [kg/m3]이다.
이 때, 유체의 총 부피는 매질의 공극률과 같으며 포화도와 질량비(mass fraction)에 따라 각 상의 부피가 나뉘게 되고 각각의 밀도를 이용해 전체 유체의 질량을 계산한다. 또한 단위 면적 당 질량 유속은 다상 Darcy의 법칙 및 Fick의 법칙을 통해 계산되는데, 이를 식 (1)에 적용하면 다음과 같은 각 상에 대한 질량 보존 방정식을 얻을 수 있다.
여기서 𝜙는 공극률(porosity), Sβ는 포화도(saturation of phase β), ρβ는 밀도(density of phase β) [kg/m3], Xκβ는 질량비(mass fraction of component κ present in phase β), k는 고유 투수율(intrinsic permeability) [m2], krβ는 상대 투수율(relative permeability in phase β), μβ는 점성도(viscosity in phase β) [Pa·s]이다.
상대 투수율은 Fatt and Klikoff(1959) 식을 이용하여 계산하였으며, 이는 다음과 같다.
| $$k_{rl}=S_e^3$$ | (3) |
| $$k_{rg}=(1-S_e)^3$$ | (4) |
| $$S_e=\frac{S_l-S_{lr}}{1-S_{lr}}$$ | (5) |
여기서 Slr는 잔류 포화도(residual saturation)이다.
마지막으로 공극수에 녹아있는 기체의 양을 계산하기 위해 Henry의 법칙을 적용하였으며, 이는 다음과 같다.
| $$x_l^a=HP_a$$ | (6) |
여기서 H는 Henry 상수, Pa는 기체의 분압 [Pa]이다.
본 연구에서는 수분 보유 곡선을 고려하지 않았는데, 1차원 기체 주입 시험에서 벤토나이트 시료가 초기부터 시험 종료 시점까지 포화도가 98 %로 완전 포화 상태에 가깝게 유지되었기 때문에 모세관압에 의한 영향은 무시하였다.
3.2 유효응력 개념을 고려한 역학 손상 모델
탄성 모델에서의 유효응력은 다음과 같이 정의된다.
| $$\boldsymbol\tau=\boldsymbol\sigma-\alpha p\mathbf I$$ | (7) |
여기서 σ는 전응력(total stress)이며, α는 Biot 상수이다.
본 연구에서는 기체 압력 증가에 따른 미세 균열 발생 및 이에 따른 역학적 거동 변화를 모사하기 위해 손상도 개념을 적용하였다. 미세 균열 발생에 의한 매질의 손상도는 0과 1 사이의 값을 갖으며, 미세 균열이 많이 발생할수록 1에 가까운 값을 갖는다. 만약 매질의 손상이 발생하였을 경우 매질의 역학적 거동 변화가 발생하는데, 이를 모사하기 위해 손상도에 따른 역학적 구성 모델(constitutive model)을 적용하였다. 암석과 같은 지반 재료 및 콘크리트에서의 손상에 따른 역학적 거동을 모사하기 위해 다양한 역학 손상 모델(mechanical damage model)이 개발되었으나(Mazars, 1986, Simo and Ju, 1987, Lee and Fenves, 1998, Jirásek, 2004, Jason et al., 2006), 벤토나이트 완충재와 같이 점토 물질을 다량 함유한 매질에 대한 역학 손상 모델은 아직 제안된 바가 없다. 따라서 본 연구에서는 벤토나이트 완충재의 역학 손상 거동을 탄성 손상 거동으로 가정하였으며, 매게 변수 불확실성(parameter uncertainty)을 줄이기 위해 가장 단순한 모델 중 하나인 Tang et al. (2002)이 제안한 탄성 손상 모델을 적용하였으며 이는 다음과 같다.
| $$\boldsymbol\sigma=(1-D)\;\mathbf C\boldsymbol:\mathbf\varepsilon$$ | (8) |
여기서 C는 탄성 계수를 뜻하며, D는 손상도를 의미한다.
만약 매질에 작용하는 응력이 인장 및 압축 강도를 넘어 매질의 파괴가 일어나는 경우, 즉 매질의 손상이 발생하는 경우 탄성 계수가 손상도에 따라 감소하게 되며, 이후 역학적인 거동은 Fig. 4와 같이 감소된 탄성 계수를 따라 발생한다(Tang et al., 2002).
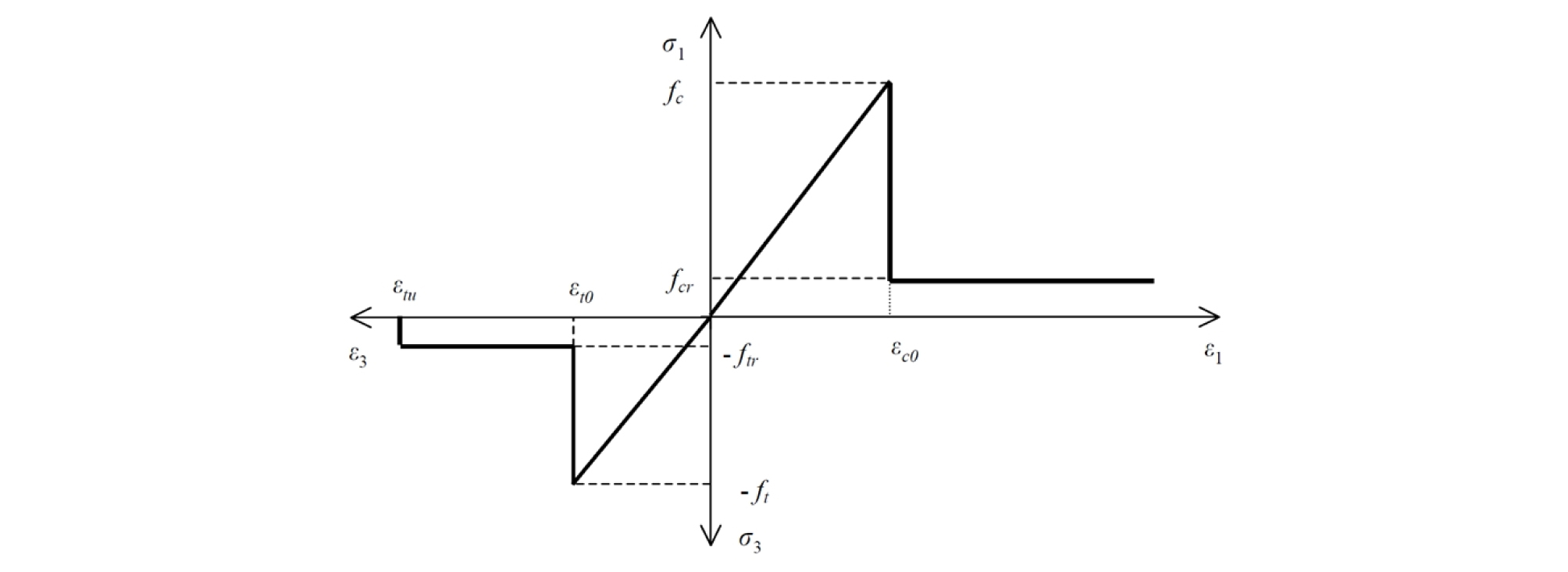
Fig. 4.
Elastic damage constitutive law for element under uniaxial compression and extension (Tang et al., 2002)
만약 매질에 작용하는 인장 응력(σ3)이 인장 강도(ft)를 넘어서는 경우, 손상도는 다음과 같이 정의된다.
여기서 ftr은 잔류 인장 강도(residual tensile strength), E0는 비손상 탄성계수(undamaged elastic modulus), εt0는 인장 파괴 시점에서의 변형률, εtu는 인장 변형률 한계(tensile strain limit), ε3은 주변형률(principal strain)을 의미한다.
기체 주입 시험의 경우 기체 주입으로 인해 공극 수압이 증가하게 되며, 이에 따라 유효 응력이 감소하게 된다. 기체가 지속적으로 주입이 될 경우 유효 응력이 계속 감소해 매질의 요소에 인장 응력이 발생하게 되는데, 만약 유효 응력이 인장 강도를 넘어서게 되면 인장 파괴가 발생할 수 있으며, 이는 기체 주입 시험에서의 주요 파괴 메커니즘에 해당한다.
압축 혹은 전단 파괴를 모사하기 위해, Mohr-Coulomb 파괴 기준식을 두 번째 파괴 조건으로 고려하였으며, 이때의 손상도는 다음과 같다.
여기서 𝜙는 마찰각, fc는 일축 압축 강도(uniaxial compressive strength), fcr은 잔류 압축 강도(residual compressive strength), εc0는 압축 파괴 시점에서의 변형률, ε1은 주변형률(principal strain)을 의미한다.
다만 기체 주입 시험과 같이 유체압이 증가하는 경우, 유효 응력의 감소로 인해 압축 파괴 조건을 만족시키지 못하기 때문에, 압축 파괴는 기체 주입 시험에서 주요 파괴 메커니즘에 해당하지 않는다.
3.3 손상도에 따른 수리 물성 변화
본 연구에서는 매질의 팽창에 의한 우선 경로를 직접적으로 고려하지 않고 손상도에 따른 등가 투수율 개념으로 고려하였다. 만약 매질의 손상 혹은 파괴가 발생한다면 공극 구조의 변화를 유발하기 때문에 유체 흐름 현상이 변화하게 된다. 따라서 손상도에 따른 투수율의 변화를 필수적으로 고려하여야만 한다. 이를 위해 손상도와 투수율의 관계를 설명한 다양한 연구들이 진행되어 왔지만(Gawin et al., 2001, souley et al., 2001, Tang et al., 2002), 본 연구에서는 Meschke and Grasberger(2003)이 제안한 방법론에 따라 투수율을 계산하였다. 만약 특정 요소에서 매질의 손상이 발생한 경우, 이 요소의 등가 투수율은 손상되지 않은 매질의 투수율(undamaged permeability)과 손상된 매질의 투수율(damaged permeability)의 합으로 계산되며(Fall et al., 2014), 이는 다음과 같다.
| $$k=k_{UD}+k_D$$ | (11) |
여기서 kUD는 손상되지 않은 매질의 투수율, kD는 손상된 매질의 투수율을 나타낸다.
손상되지 않은 매질이라도 응력 변화에 의해 투수율이 변화하며(Davis and Davis, 1999, Rutqvist et al., 2002), 이는 다음과 같다.
| $$k_{UD}=k_0\exp\left[A\left(\frac{\mathit\phi}{{\mathit\phi}_{\mathit0}}\mathit-\mathit1\right)\right]$$ | (12) |
여기서 k0는 초기 고유 투수율, A는 비손상 투수율 계수(undamaged permeability factor), 𝜙0는 초기 공극률이며, 암석 광물과 같은 고체 입자의 부피 변화는 고려하지 않았기 때문에 매질의 부피 변화는 공극 부피의 변화와 같다.
| $$\phi=\frac{V_{pore}+\bigtriangleup V}{V+\bigtriangleup V}$$ | (13) |
손상된 매질의 투수율은 손상도에 비례하여 감소하며 이는 다음과 같다.
| $$k_D=\frac D{D_{k_\max}}(k_\max-k_{UD})$$ | (14) |
여기서 Dkmax는 최대 손상도, kmax는 최대 손상도 일 때의 투수율을 의미한다.
3.4 해석 모델
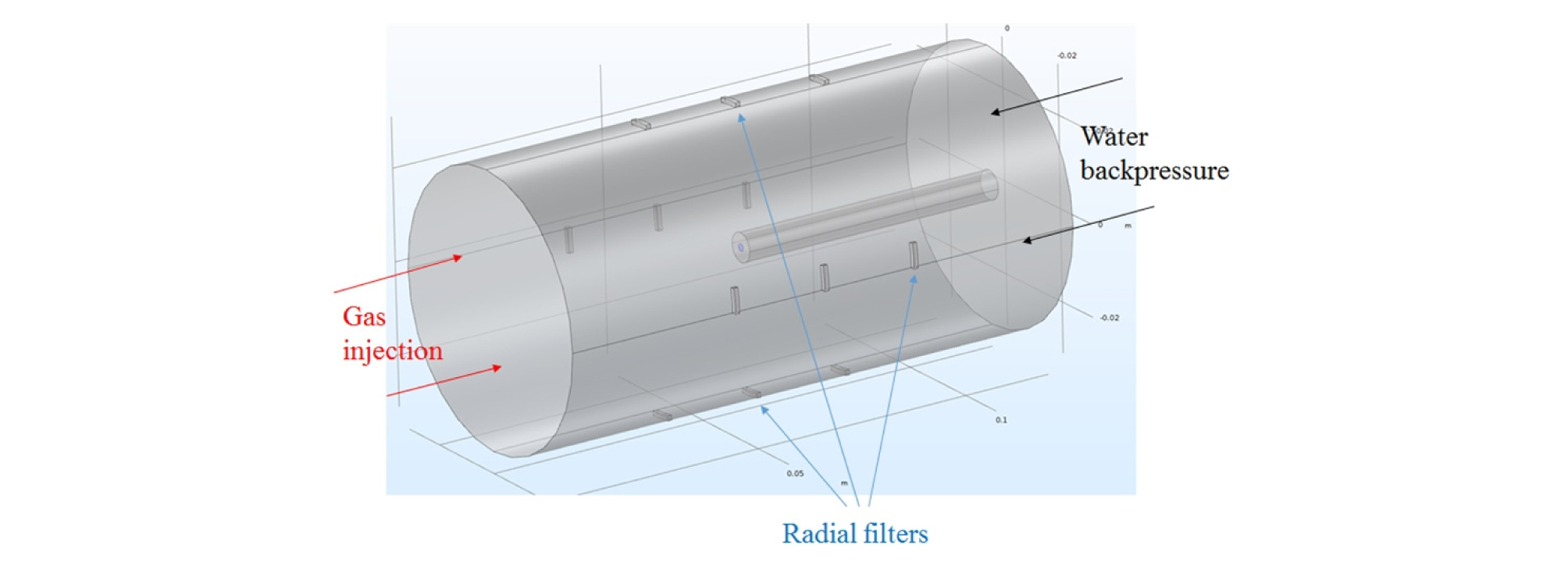
일정 체적 경계 조건 하에서의 1차원 기체 주입 시험 모사를 위해 3차원 모델을 이용하였으며, 벤토나이트 시료의 크기는 직경 60 mm, 길이 120 mm 이고, 스테인리스 강 튜브의 크기는 직경 6.35 mm, 길이 64.8 mm 이다(Fig. 5). 스테인리스 강 튜브는 벤토나이트 시료 중앙에 기체를 주입하기 위해 고안되었으나, 본 시험에서는 벤토나이트 시료의 측면에서 기체 주입을 실시하였기 때문에 경계 조건의 역할만을 수행한다. 해석 모델의 총 요소의 개수는 7560 개 이며, 6면체 요소를 사용하였다.
3.4.1 초기 조건 및 경계 조건
벤토나이트 시료는 초기에 1.0 MPa의 수압 및 98 % 포화도를 갖는다. 또한 5.5 MPa의 팽윤압(swelling pressure)이 존재한다고 가정하였다. 초기 응력 측정 결과 기체 주입을 실시하기 전 벤토나이트 시료의 팽윤(swelling)으로 인해 5.5 MPa의 응력이 걸리는 것으로 확인되었지만, 수치 모델에서는 포화도의 변화가 발생하지 않기 때문에 추가적인 팽창압이 발생하지 않는다. 따라서 이를 보완하기 위해 초기 응력을 5.5 MPa로 가정하였다.
역학 경계 조건은 일정 체적 경계 조건을 모사하기 위해 고정 경계 조건(Fixed boundary condition)을 이용하였다. 수리 경계 조건은 Fig. 5에서와 같이 스테인리스 강 튜브가 없는 면은 기체 주입을 위해 일정 유량 경계 조건(constant flux boundary condition)을 적용하였으며, 반대면 및 반경 필터(radial filter)에서는 일정 수압 경계 조건(constant pressure boundary condition)을, 반경 필터(radial filter)를 제외한 나머지 옆면은 no flow 경계 조건을 적용하였다.
3.4.2 물성
본 해석에 사용된 물성은 Table 3에 나타나 있다. 탄성 계수, 포아송 비, 공극률, 고유 투수율은 Task 제안 기관인 BGS에서 제공한 물성이고, 압축 강도, 잔류 압축 강도, Biot 상수, 입자 밀도, 잔류 포화도, 비손상 투수율 계수, 최대 손상도는 참고문헌에서 얻은 값이며, 그 외 나머지 물성은 가정한 값이다.
Table 3. Properties of bentonite sample
3.5 모델링 스케쥴
BGS에서 수행한 일정 체적 경계 조건 하에서의 1차원 기체 주입 시험을 모사하기 위해 총 4 단계로 나누어 해석을 진행하였다(Table 4). 1 단계에서는 벤토나이트 시료를 포화시키기 위해 기체 주입 필터(injection filter) 및 배압 필터(backpressure filter)를 1 MPa의 일정 수압 조건으로 유지시켰으며, 2 단계에서는 기체 주입을 실시하기 위해 기체 주입 필터에서 3 MPa의 일정 압력 조건으로 기체를 주입하였다. 3 단계에서는 선형으로 증가하는 기체 주입량 조건을 이용해 본격적으로 기체 주입을 실시하였으며, 4 단계에서는 통로 밀봉 현상(pathway sealing)을 확인하기 위해 기체 주입을 실시하지 않은 상태를 유지하였다.
Table 4. Modelling schedule
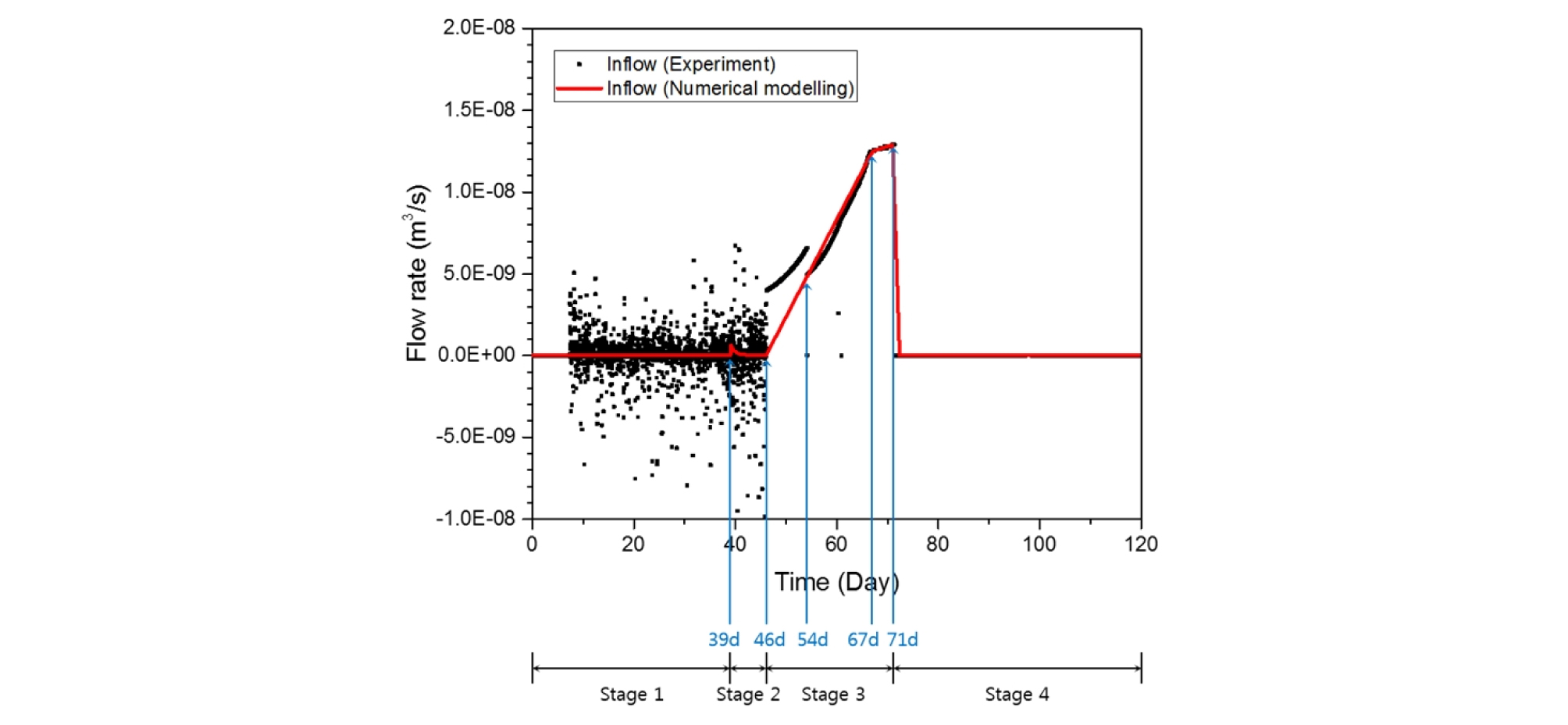
Fig. 6은 모델링 스케쥴에 따른 벤토나이트 시료로 들어가는 기체 주입량(flowrate) 결과를 비교한 그림이다. 2 단계에서 기체 압력을 3 MPa로 증가시켰기 때문에 초기에 약간의 기체 주입량이 발생하였다. 3 단계의 경우 54일까지는 실험실 시험 결과에 비해 낮은 기체 주입량을 모사하였으며, 그 이후에는 시험 결과와 유사한 주입량을 모사하였다. 3 단계 중 46 일부터 54일까지 낮은 주입량으로 모델링을 수행한 이유는 실험실 시험 결과와 동일한 주입량으로 모델링을 하였을 경우 3 단계 초기에 기체 압력이 급격하게 증가하는 현상이 발생하였기 때문에, 실제 시험 결과에 비해 낮은 값으로 가정 후 수치해석을 수행하였다.
4. 해석 결과
1차원 기체 주입 시험 결과, 기체 주입으로 인해 공극 수압이 증가하였으며 특정 기체 주입 압력(약 8.5 MPa)을 넘었을 때 기체가 급격히 벤토나이트 시료로 들어가게 되는 팽창 흐름 현상이 관찰되었다. 벤토나이트 시료 부피를 일정하게 유지시키기 위한 구속 경계 조건으로 인해 벤토나이트에서의 미세 균열 생성 및 전파로 인한 요소 부피 증가 현상 대신 응력이 증가하였으며, 팽창 흐름으로 인해 배압 필터에서의 기체 유출량의 급격히 발생하는 현상이 관찰되었다.
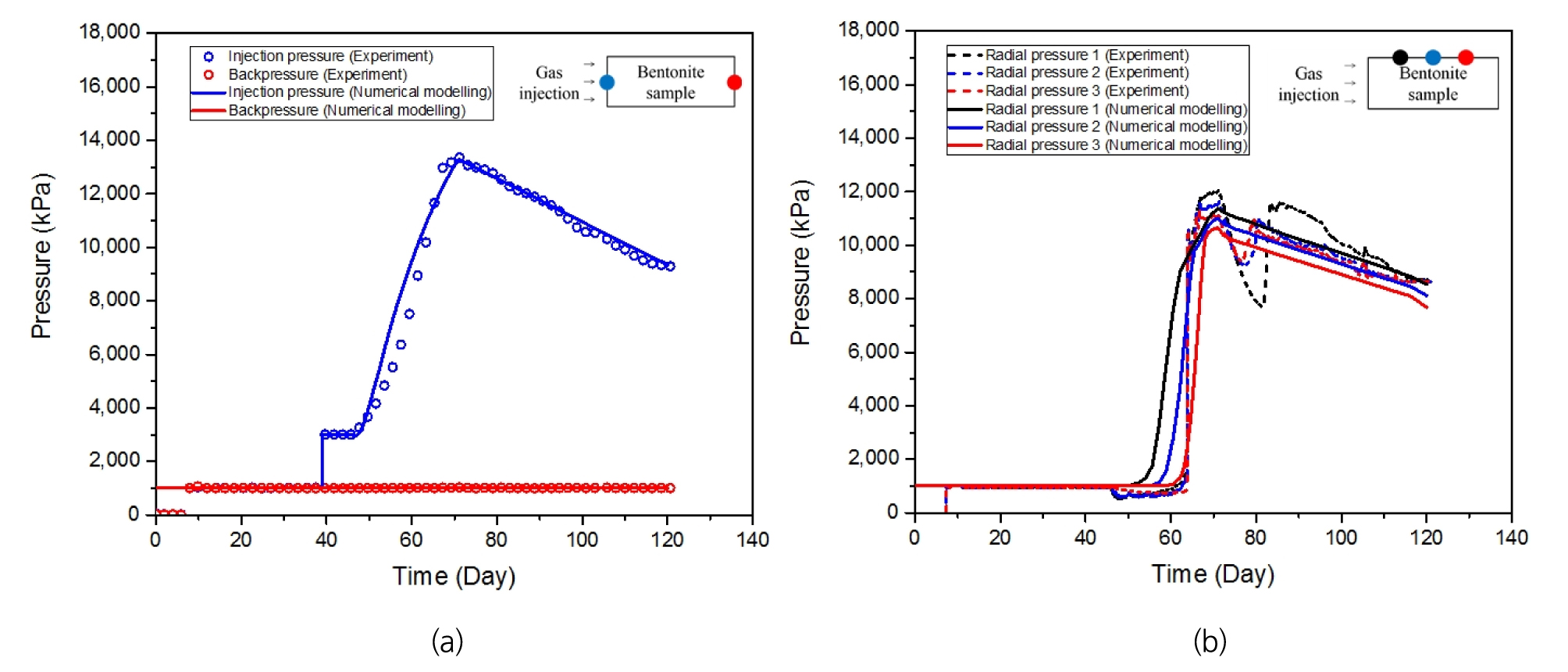
Fig. 7은 일정 체적 경계 조건 하에서의 1차원 기체 주입 시험에 대한 기체 주입 필터, 배압 필터, 그리고 반경 필터에서의 공극 수압 변화를 나타낸 그림이다. 기체 주입 필터에서 공극 수압 결과는 실험실 시험 결과와 유사한 경향을 나타냈으며, 특히 최대 공극 수압 및 피크 이후(post-peak) 거동이 거의 일치하는 것으로 나타났다. 하지만 최대 공극 수압 이전의 거동의 경우, 수치 모델링은 초기에 급격한 압력 증가 현상을 보이다가 점차 기울기가 감소하였는데 실내 시험 결과는 기울기가 점차 증가하는 형태로 나타났다. 수치 모델링의 경우 벤토나이트 시료 옆면에 직접적으로 기체를 주입하는 반면, 실험실 시험의 경우 기체 주입 펌프를 이용해 기체 주입 필터를 거쳐 기체 주입이 이루어지기 때문에 압력 증가 반응에 차이가 발생한 것으로 판단된다. 또한 수치 해석의 경우 손상도가 벤토나이트 시료 전 영역에 걸쳐 발생하기 때문에 손상도가 진행될수록 벤토나이트 시료로 주입되는 기체양이 늘어나면서 압력 증가 기울기가 감소하지만, 실험실 시험의 경우 특정 통로를 통해서만 기체가 주입되기 때문에 압력 증가 기울기가 다르게 나타난 것으로 판단된다. 배압 필터는 시험 과정 및 모델링에서 동일하게 1 MPa의 수압으로 일정하게 유지되었기 때문에, 결과 차이가 발생하지 않았다.
반경 필터의 경우 특정 시점에서 공극 수압이 갑작스럽게 증가하는 현상을 확인할 수 있는데, 이는 기체 압력에 따른 팽창 흐름이 발생하였기 때문이다. 수치 해석 결과 반경 필터에서의 갑작스러운 공극 수압 증가 현상을 확인할 수 있었으며, 최대 공극 수압 및 피크 이후 거동도 실험실 시험 결과와 거의 일치하는 것으로 나타났다. 다만 실험실 시험 결과는 필터의 위치에 상관없이 거의 동시에 압력이 급격히 증가하였으나, 수치 해석 결과는 필터의 위치에 따라 압력 증가 현상 발생 시점이 다르게 나타났다. 수치 해석의 경우 손상도가 기체 주입 필터에서부터 배압 필터로 점진적으로 발생하기 때문에 반경 필터의 위치에 따라 압력 증가 발생 시점이 다르게 나타났으며, 이는 본 연구에서 개발된 모델의 한계점을 나타낸다.
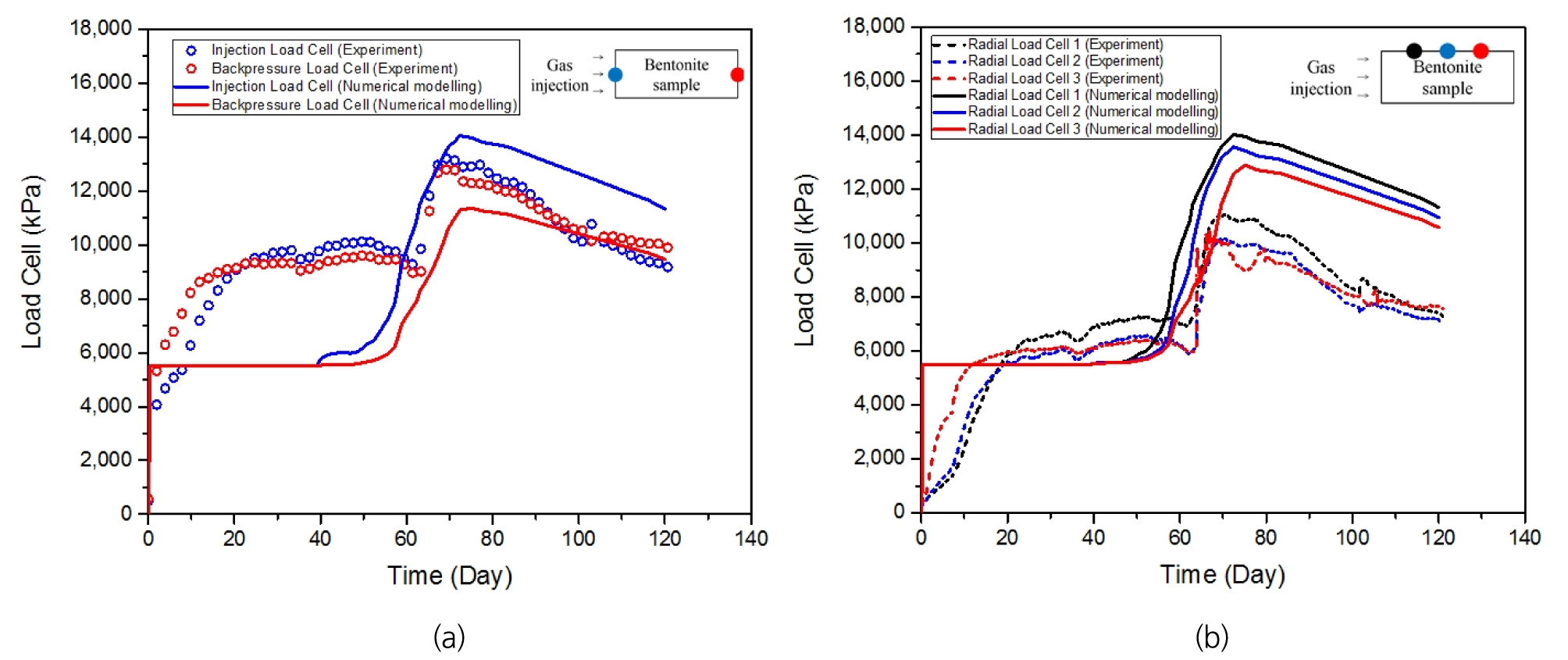
Fig. 8은 일정 체적 경계 조건 하에서의 1차원 기체 주입 시험에 대한 기체 주입 필터, 배압 필터, 그리고 반경 필터에서의 응력 변화를 나타낸 그림이다. 실험실 시험의 경우 시간이 지남에 따라 팽윤압이 계속 발생하면서 팽창 흐름이 발생하기 이전 최대 약 10 MPa에 달하는 응력이 측정되었으나, 앞서 설명한 대로 수치 해석에서는 포화도의 변화가 발생하지 않기에 추가적인 팽윤압이 발생하지 않아 초기 조건으로 가정한 5.5 MPa의 응력을 유지하였다. 팽창 흐름 발생 이후 응력 또한 급격히 증가하는 현상이 나타났으며, 최대 응력 이후 점차 응력이 감소하였다. 수치 해석 결과 응력 증가 현상 및 최대 응력 이후 감소하는 경향은 모사할 수 있었으나, 최대 응력 값에서 차이가 발생하였고 응력 증가 기울기나 최대 응력 이후 응력 감소 기울기가 실험실 결과에 비해 다소 완만하게 나타났다. 최대 응력 값의 경우 기체 주입 필터의 로드셀에서는 수치 해석 결과가 실험실 시험 결과에 비해 약 1 MPa 정도 높게 나타났으며, 배압 필터의 로드셀에서는 약 2 MPa 정도 낮게, 반경 로드셀의 경우 약 3 MPa 정도 높은 결과를 나타냈다. 수치 해석의 경우 손상도가 기체 주입 필터에서부터 배압 필터로 점진적으로 발생하기 때문에 기체 주입 필터에서 응력이 가장 높게 나타났으며, 배압 필터 쪽으로 갈수록 응력이 낮게 나타남을 확인할 수 있었다. 수치 해석 결과 응력 증가 및 응력 감소 기울기가 실험실 시험 결과에 비해 완만하게 나타났는데, 이는 본 연구에서 개발된 해석 모델에서 수리-역학적 상호작용의 영향이 과소평가됨을 의미하기에, 모델 개선에 관한 추가적인 연구가 필요하다.
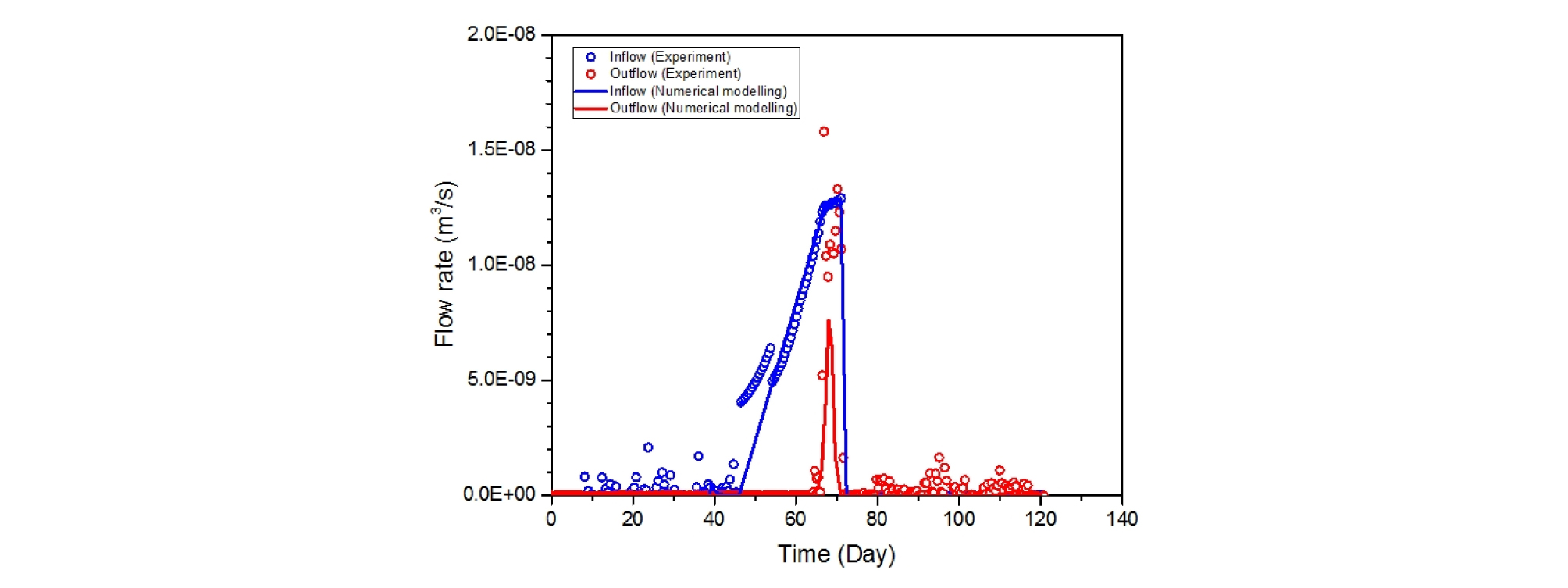
Fig. 9는 일정 체적 경계 조건 하에서의 1차원 기체 주입 시험에 대한 기체 주입량과 유출량을 나타낸다. 기체 주입량의 경우 4 단계로 나누어 주입을 실시하였으며, 3 단계 초기의 경우 과도한 기체 주입 압력 증가 현상을 방지하기 위해 실험실 시험 결과보다 낮은 주입량으로 가정 후 수치해석을 진행하였다 (Fig. 6). 배압 필터에서의 기체 유출량이 팽창 흐름 발생 시 급격히 증가하는 현상을 모사할 수 있었지만, 최대 기체 유출량 값이 실험실 시험 결과에 비해 약 1.0E-8 m3/s 정도 낮게 나타남을 확인할 수 있었다. 이는 실험실 시험의 경우 특정 통로를 통해서만 기체 흐름이 발생하지만 수치 해석의 경우 손상도가 벤토나이트 시료 전 영역에 걸쳐 발생하기 때문에, 수치 해석에서 벤토나이트 시료가 저장하고 있는 기체의 양이 실험실 시험에 비해 많기 때문인 것으로 판단된다.
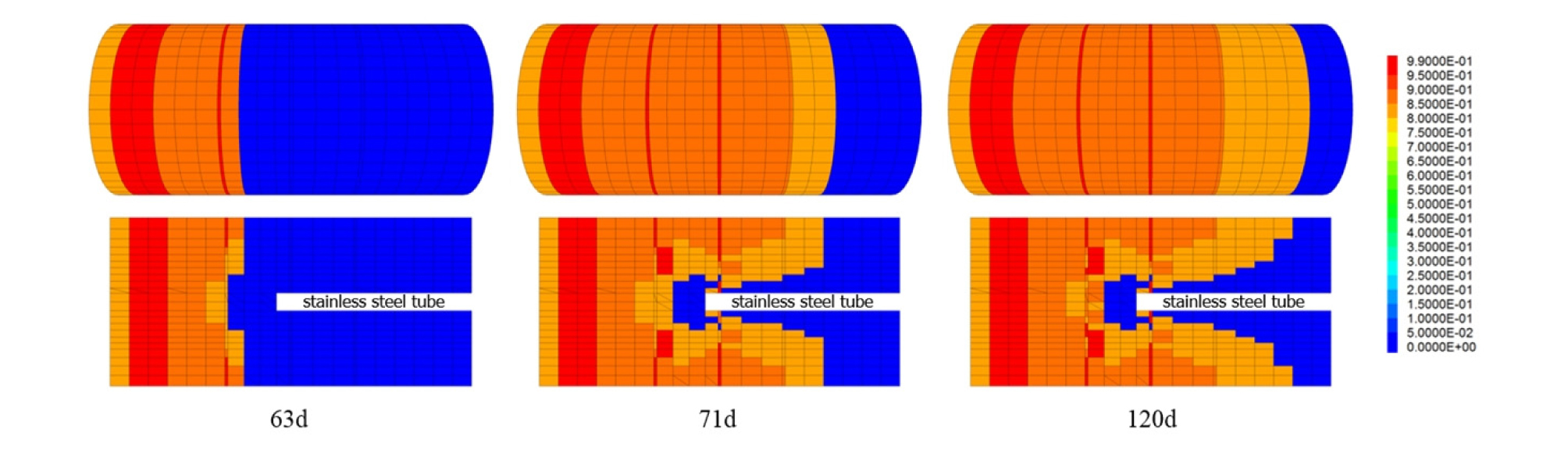
마지막으로 Fig. 10은 시간에 따른 손상도 변화를 나타낸 그림이다. 손상도는 0에서 1 사이의 값을 갖으며, 1에 가까울수록 매질이 많이 손상되었음을 의미한다. Fig. 10을 통해 벤토나이트 시료 내부에서 손상도는 기체 주입 필터에서부터 배압 필터로 점진적으로 발생함을 확인할 수 있었다. 또한 스테인리스 강 튜브 주변에서는 다른 지점에 비해 상대적으로 손상이 거의 발생하지 않았는데, 이는 유체 흐름 통로와 관련이 있는 것으로 판단된다. 반경 필터는 시험 기간동안 1 MPa의 압력으로 유지되기 때문에 완전한 1차원 유체 흐름이 아닌 반경 필터 방향으로의 유체 흐름이 나타났으며, 이에 따라 스테인리스 강 튜브 주변부 보다 반경 필터에 가까운 요소들의 유체 압력이 높게 나타났다. 따라서 반경 필터 주변의 요소들이 인장 파괴가 먼저 발생하게 되고, 인장 파괴에 의해 투수율이 급격히 증가함으로써 반경 필터 방향으로의 유체 흐름이 강화되는 현상이 나타났다. 결과적으로 스테인리스 강 튜브 주변부에서의 공극 수압은 파괴를 일으킬 만큼 증가하지 않아, 스테인리스 강 튜브 주변부는 상대적으로 손상이 거의 발생하지 않은 것으로 판단된다.
5. 결 론
고준위방사성폐기물처분장에서 공학적 방벽은 최소 수 백년 이상 방사성 핵종 누출 억제 역할을 수행해야 하기에 장기 건전성 확보 측면에서 기체 이동 현상을 명확히 규명하는 것이 매우 중요하다. 특히 벤토나이트 완충재와 같이 점토 물질을 다량 함유한 매질에서만 나타나는 매우 중요한 기체 흐름 현상인 팽창 흐름에 대한 수리-역학적 메커니즘을 규명하고, 기체 이동 현상의 정량적 평가를 위한 새로운 수치 해석 기법 개발 및 검증이 필수적이다. 따라서 본 논문에서는 공학적 방벽에서의 기체 이동 현상을 모사하고자 역학 손상 모델 및 손상도를 고려한 2상 유동 모델을 개발하였으며, 일정 체적 경계 조건 하에서의 1차원 기체 주입 시험 모사를 통해 개발된 모델의 적용성을 검토하였다.
모델 개발의 경우 벤토나이트 완충재의 공극에서의 기체상 유동 및 액체상에 녹아있는 기체의 유동을 고려하기 위해 다공성 매질에서의 2상 유동을 고려하였으며, 공극 수압의 변화로 인한 매질의 손상도(damage)를 판단하기 위해 유효응력 개념을 고려한 역학 손상 모델을 적용하였다. 또한 손상도에 따른 수리 물성 변화를 고려함으로써 매질의 변형에 의한 기체의 팽창 흐름을 모사하였다.
모델 적용성 검토를 위해 3차원 모델을 이용하여 일정 체적 경계 조건 하에서의 1차원 기체 주입 시험 모사를 수행하였다. 4 단계로 나누어 기체 주입을 실시하였으며, 3 단계 초기의 경우 과도한 기체 주입 압력 증가 현상을 방지하기 위해 실험실 시험 결과보다 낮은 주입량으로 가정 후 수치해석을 진행하였다. 수치해석 결과 기체 주입 필터에서 공극 수압 결과는 실험실 시험 결과와 유사한 경향을 나타냈으며, 특히 최대 공극 수압 및 피크 이후 거동이 거의 일치하는 것으로 나타났다. 또한 수치 해석 결과 응력 증가 현상 및 최대 응력 이후 감소하는 경향은 모사할 수 있었으며, 배압 필터에서의 기체 유출량이 팽창 흐름 발생 시 급격히 증가하는 현상을 모사할 수 있었다. 하지만 기체 주입 필터에서부터 배압 필터로 점진적으로 발생하는 손상도로 인해 공극 수압 증가 시점에서 차이가 발생하였으며, 응력 증가 기울기나 최대 응력 이후 응력 감소 기울기가 실험실 결과에 비해 다소 완만하게 나타나는 등 현재 개발된 해석 모델이 수리-역학적 상호작용의 영향을 과소평가 하는 한계를 확인할 수 있었다. 추후 DECOVALEX-2019 Task A 워크숍을 통해 국외 연구팀들과 서로의 연구결과를 공유하고 의견을 교류함으로써 본 연구에서 개발된 수치 해석 모델을 지속적으로 개선해 나가는 한편, 추가적인 해석을 통해 모델 적용성을 검토할 예정이다.