1. 서 론
2. 현장조사
3. 진동파형의 추정
3.1 이론적 및 경험식을 이용한 발파압력이력곡선의 추정
3.2 진동파형의 현장계측
3.3 입력진동파형의 추정
4. 동적수치해석 기법을 이용한 갱내채광장의 안정성 평가
4.1 수치모델 및 해석조건
4.2 입력물성 산정
4.3 해석결과
5. 결 론
1. 서 론
최근 채광기술의 발달로 인하여 채광장을 대규모화하고 채수율의 향상을 도모하는 설계가 검토되고 있다. 일반적으로 최소한의 지보를 적용하는 채광장에서는 안정성이 확보되는 범위에서의 광주와 채굴공동의 형상을 주요 설계요인으로 고려하며, 채광장에서의 안정성은 암반의 강도, 암반 내 불연속면, 현지응력 등의 환경적인 요인과 발파 및 교통 하중 등의 인위적인 요인을 모두 고려하여 분석하여야 한다. 특히 광산에서는 채광작업을 위한 지속적인 발파작업에 노출되기 때문에, 발파작업에 의한 발파하중을 고려한 채광장의 안정성 분석이 필수적이다.
발파하중은 암반에 분포하는 불연속면과 같은 지질구조와 화약의 종류 및 장약량 등의 발파조건에 따라 진동의 전파특성이 달라지므로, 직접적인 계측, 동적수치해석 등의 기법을 이용하여 발파진동에 대한 영향을 검토하게 된다.
Chen and Zhao(1998)는 암반에 분포하는 절리의 영향을 고려하기 위하여 불연속체 개발요소 프로그램을 이용하여 발파진동의 전파특성을 연구하였고, Choi et al.(2004)는 사실적인 발파 동해석을 모사하기 위하여 시험발파에서 측정된 발파진동파형을 이용하여 동해석의 입력 자료로 이용하였으며, 동압력의 시간이력과 감쇠비에 따른 영향을 분석하였다. Park et al.(2008)은 단일공 및 시추공 발파 진동파형을 중첩모델링하여 발파공수와 지연시차의 변화에 따른 진동파형을 획득하고, 이를 발파 동적수치해석의 발파하중으로 적용하여 구조물의 안정성을 평가하였다.
본 연구에서는 갱내채광장의 발파현상을 현실적으로 모사하기 위하여 현장에서의 발파를 통해 획득한 발파 진동파형을 발파지점의 진동속도로 변환하였으며, 이를 동적수치해석의 입력 자료로 이용하였다. 또한 암반에 분포하는 절리의 영향을 고려하기 위하여 불연속체 수치해석 프로그램인 UDEC을 이용하였으며, 석회석 갱내채광장의 작업과정과 실측발파진동을 반영한 동적수치해석을 수행하고, 이를 바탕으로 발파진동이 갱내채광장의 안정성에 미치는 영향을 분석하였다.
2. 현장조사
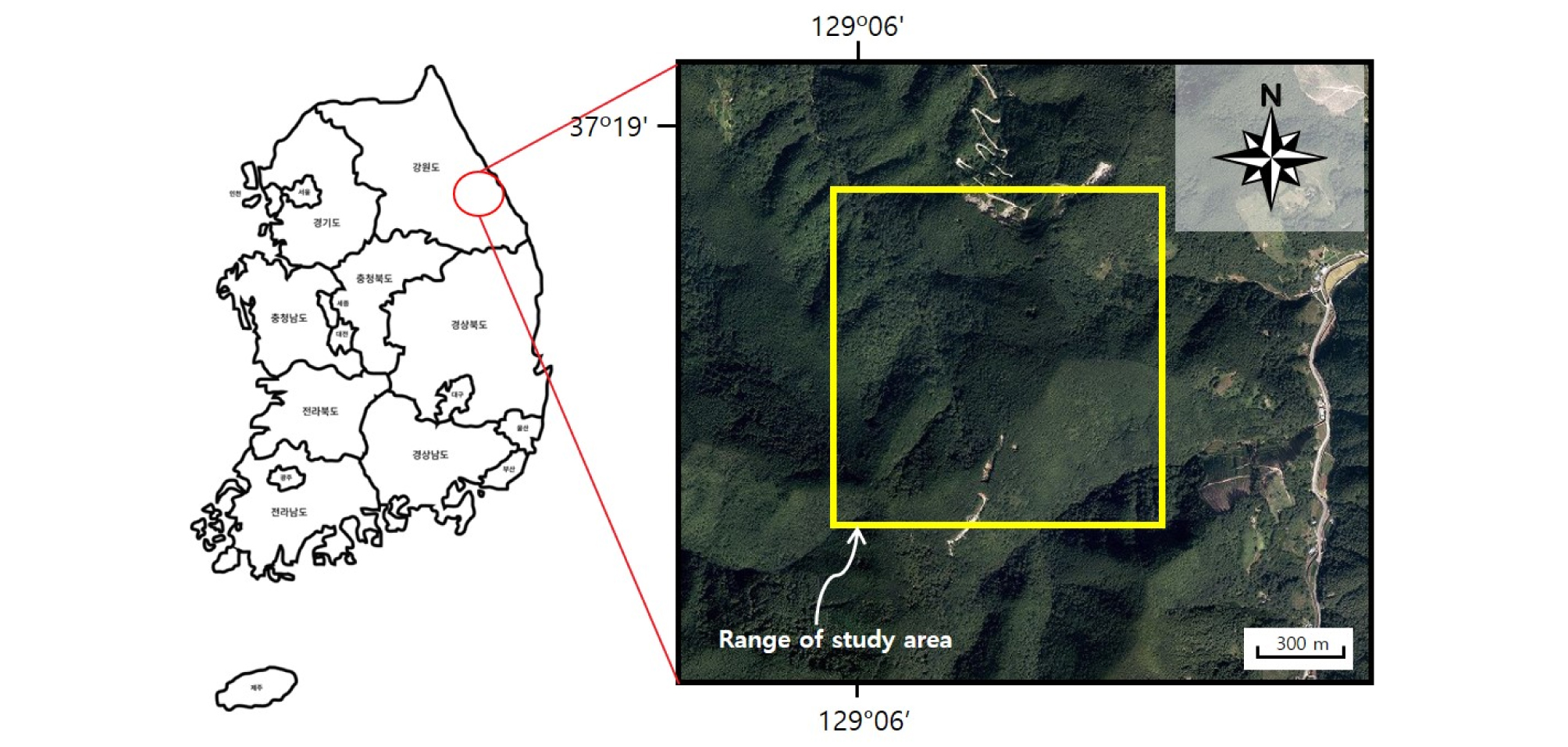
본 연구에서 대상으로 하는 광산은 강원도 삼척시 신기면에 위치한 갱내 석회석 광산으로, 고생대 캠브리아기의 풍촌층을 대상으로 채광 작업을 수행하고 있다(Fig. 1).
본 지역에 분포하는 절리군의 특성과 암반상태를 규명하기 위하여 갱내 석회석 광산의 520 ML과 540 ML 채굴공동의 절리면 조사와 암반분류를 수행하였다.
절리면에 대한 조사는 채굴공동과 광주에 노출되어 있는 절리면을 대상으로 절리군의 분포와 방향성을 분석하였으며, 절리면의 연속성, 틈새, 충전물, 풍화 정도를 함께 조사하여 암반상태의 평가에 이용하였다.
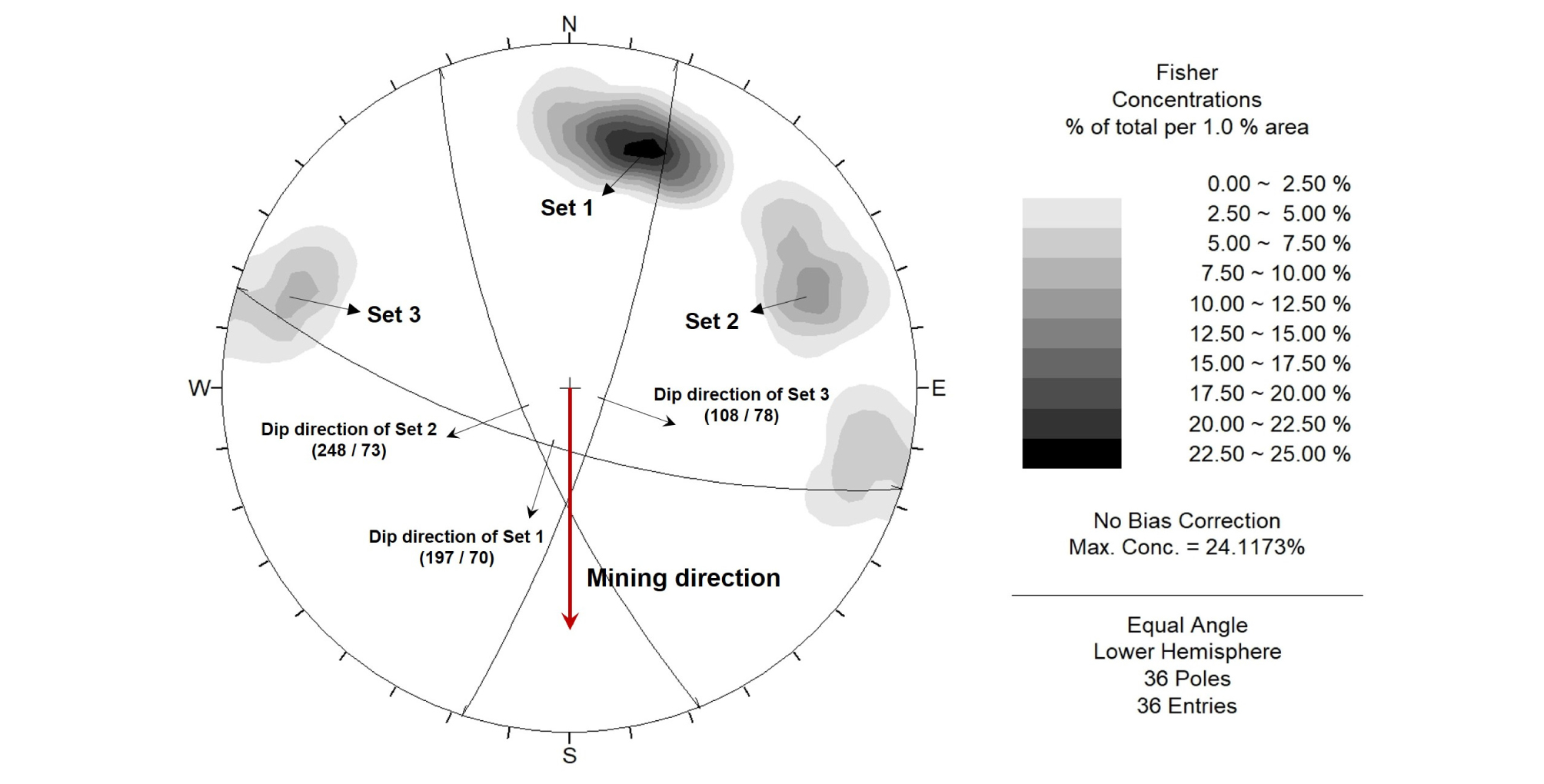
절리군의 분포와 방향성을 분석하기 위하여 현장에서 조사된 값을 기반으로 Rocscience의 Dips를 이용하였으며, 분석된 절리군의 분포와 방향성은 Fig. 2와 같다. Table 1에서 확인할 수 있듯이, 본 연구지역에는 3개의 주절리군이 형성되어 있으며, 187~210°의 경사방향과 70° 이상의 급경사를 갖는 주절리군의 분포가 가장 우세한 것으로 나타났다. 또한 조사된 절리면의 분포가 주절리군의 극점으로부터 매우 낮은 분산도를 나타내고, 급경사의 Set-1과 Set-3의 주절리군이 직교하는 형태로 분포하고 있기 때문에, 절리군의 거동특성에 대한 고려가 필요할 것으로 판단된다.
조사현장에 노출된 주절리군의 절리간격은 조사시의 안전성 문제로 인하여 동일한 지역에서 조사된 Kwon et al.(2016)의 결과를 이용하였다.
Table 1. Distribution of discontinuities in study area
| Survey location | Joint set - 1 | Joint set - 2 | Joint set - 3 | |||
| Dip dir. (°) | Dip (°) | Dip dir. (°) | Dip (°) | Dip dir. (°) | Dip (°) | |
| 520 ML | 190 | 71 | 252 | 74 | 280 | 88 |
| 540 ML | 202 | 71 | 110 | 78 | 239 | 73 |
| Total | 197 | 70 | 248 | 73 | 108 | 78 |
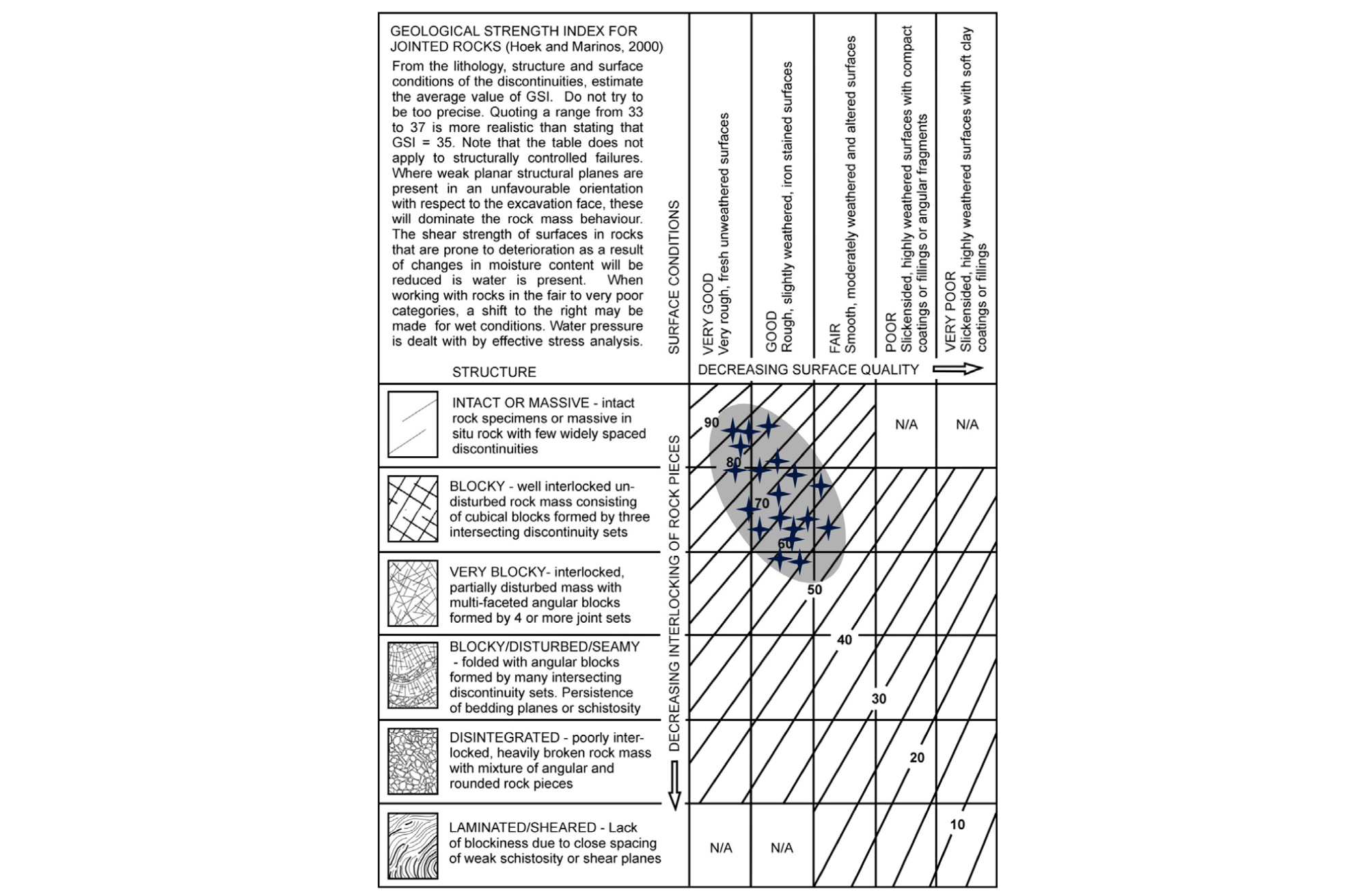
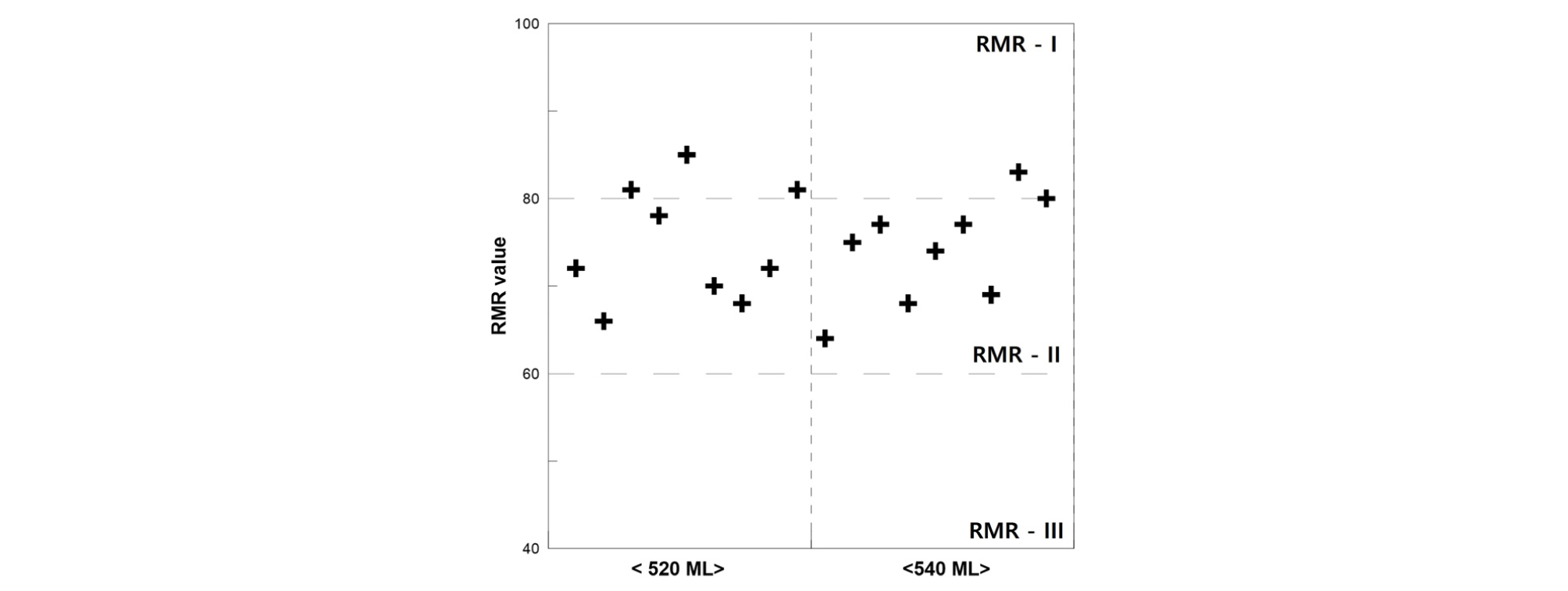
광업 및 토목 분야에서 널리 이용되며, 높은 적용성을 갖는 Hoek et al.(1998)의 GSI 분류법과 Bieniawski(1989)의 RMR 분류법을 이용하여, 갱내 석회석 광산의 520 ML과 540 ML 채굴공동의 암반상태를 정량적으로 평가하였다.
Fig. 3은 GSI 분류법을 이용하여 520 ML과 540 ML 채굴공동의 암반상태를 평가한 결과이다. GSI 값은 56에서 85까지의 범위를 가지며, 평균 70.72의 GSI 값을 나타내고 있다. 동일한 지역의 암반을 대상으로 RMR 분류법을 적용한 결과는 Fig. 4와 같으며, 최소 64 점에서 최대 85 점의 RMR 값 범위와 평균 74.44 점, RMR-II 등급의 양호한 암반상태를 나타내는 것으로 분석되었다.
3. 진동파형의 추정
수치해석에서는 복잡한 발파패턴에 의한 발파현상을 정확하기 모사하기 어렵기 때문에, 수치모델의 경계면에 발파하중을 적용하는 방식으로 발파현상을 모사하게 된다. 여기서 입력 자료로 이용되는 발파하중은 이론적인 계산식 및 경험식에 의해 추정된 발파하중을 일반적으로 이용하고 있으나, 이는 단순한 파의 형태인 것으로 발파진동을 간주하여 적용하기 때문에 실제 발파현상을 모사할 수 없다는 단점을 가지고 있다.
본 연구에서는 이러한 단점을 보완하기 위하여, 매회 발파가 수행되는 갱내 채굴공동의 상부 채굴공동에서 이격 거리를 변화하여 발파진동을 측정하였으며, 이로부터 측정된 발파진동과 발파진동파형을 근거로 발파지점의 진동파형에 관한 추정식을 산정하였다. 또한 추정된 진동파형을 수치모델의 경계면에 적용하기 위하여 20 m 이격된 거리에서 측정된 발파진동을 발파경계면에서의 진동파형으로 보정하였다.
3.1 이론적 및 경험식을 이용한 발파압력이력곡선의 추정
발파하중을 추정하는 이론적 계산식 및 경험식은 Winship and Stoneham(1987), National Highway Institute(1991) 등의 연구자들에 의하여 제시되고 있으며, 대부분 폭약의 밀도와 폭굉속도를 입력변수로 사용하고 있다. 본 연구에서는 국내에서 발파하중의 추정에 가장 널리 사용되는 National Highway Institute의 발파압력 제안식을 이용하였으며, 제안식은 식 (1)과 같다.
| $$P_d=\frac{4.18\times10^{-7}\times SG_e\times V_e^2}{1+0.8\times SG_e}$$ | (1) |
여기서, Pd : Detonation pressure (kbar)
SGe : Explosive density (g/cm3)
Ve : Detonation velocity (ft/sec)
실제로 발파에 의해 작용하는 동압력은 시간에 따라 변하는 형태를 나타내기 때문에, 동압력의 시간이력을 현실적으로 반영하여야 한다. 일반적으로 많이 적용되는 감쇠함수는 Starfield and Pugliese(1968)이 제안한 Window function로 이를 사용하여 동압력에 대한 시간이력을 산정한다.
| $$P_d(t)=4P_B\left\{\exp\left(\frac{-Bt}{\sqrt2}\right)-\exp(-\sqrt2Bt)\right\}$$ | (2) |
여기서, PB : Decoupled detonation pressure (kbar)
B : Load constant(=16,338)
t : Time (sec)
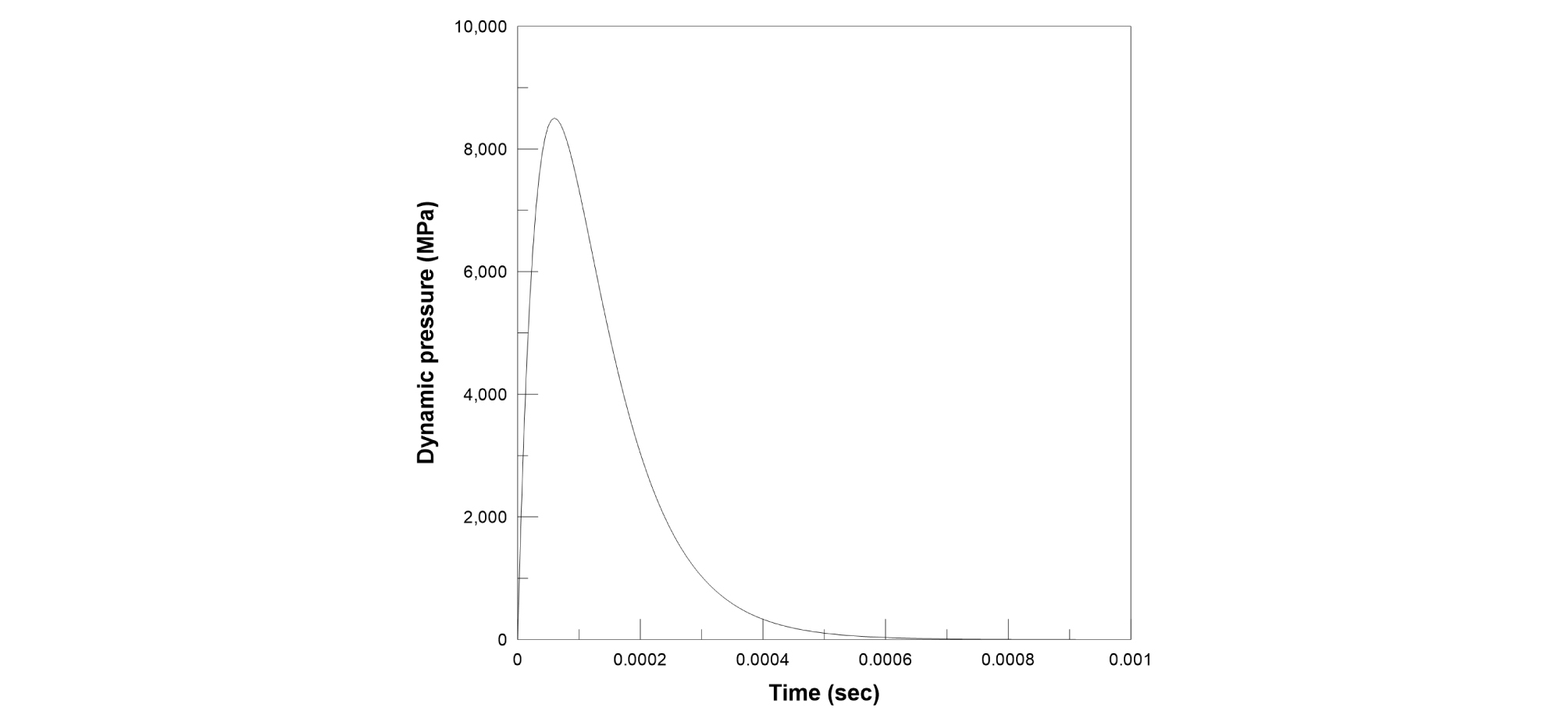
본 연구에서는 대상광산에서 사용중인 밀도 1.25 g/cm3, 폭속 5,900 m/sec의 ANFO와 에멀젼의 비율이 30 : 70인 벌크에멀젼 폭약을 대상으로 동압력에 대한 시간이력을 산정하였다(Fig. 5). Fig. 5의 동압력 대한 시간이력은 단일공의 1 kg의 폭약을 대상으로 하기 때문에, 본 연구대상 광산의 발파조건인 공당 장약량 4 kg, 전체 발파공수 68 공을 고려하여 동압력에 대한 시간이력을 보정하였다.
3.2 진동파형의 현장계측
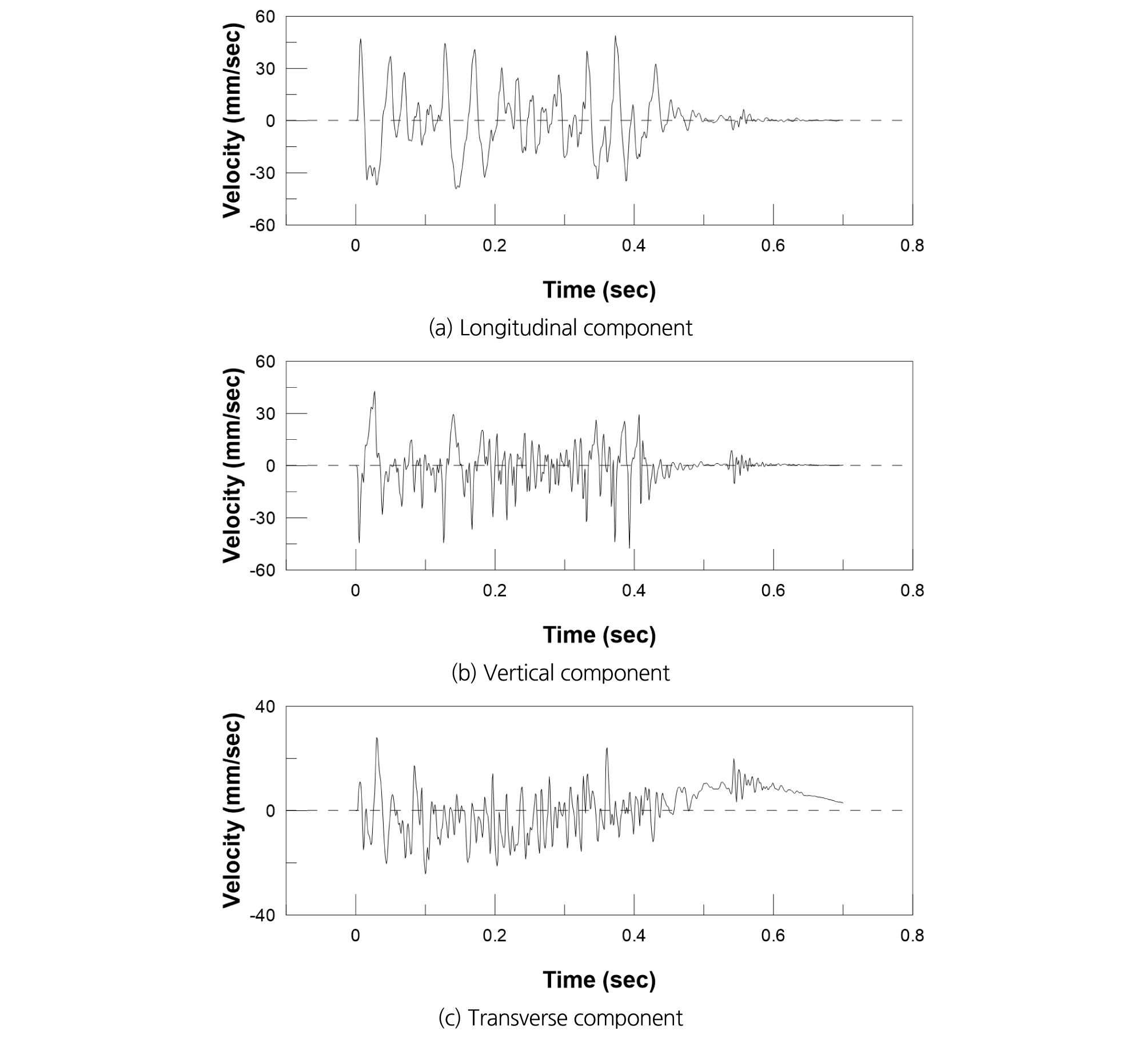
발파 동해석의 입력 자료인 실측진동파형을 추정하고자, 발파가 수행되는 520 ML 채굴공동의 상부에 위치하는 540 ML 채굴공동에 Fig. 6과 같이 2기의 발파진동 측정기를 서로 다른 거리에 설치하여 발파진동을 측정하였다. 이때 사용된 발파진동 측정기는 Instantel의 Blastmate-II 모델과 에스브이(주)의 SV-1 모델이다. 총 6회의 발파를 통하여 12 개의 발파진동 측정값을 획득하였으며, Fig. 7은 발파지점으로부터 20 m 떨어진 지점에서의 Blastmate-II 모델을 이용하여 측정된 입자속도 파형을 도시한 것이다.
3.3 입력진동파형의 추정
본 연구에서 획득한 12개의 발파진동 측정값에 식 (3)과 통계적인 방법을 적용하여 발파진동식을 추정하였다.
| $$v=k(SD)^{-e}$$ | (3) |
| $$SD=\frac D{\sqrt Q}\;\mathrm{or}\;\frac D{\sqrt[3]Q}$$ | (4) |
여기서, v : Peak vibration (mm/sec)
k : Site constant
D : Distance (m)
Q : Instantaneous charge mass (kg)
e : Site exponent
: Scaled distance (square root)
: Scaled distance (cube root)
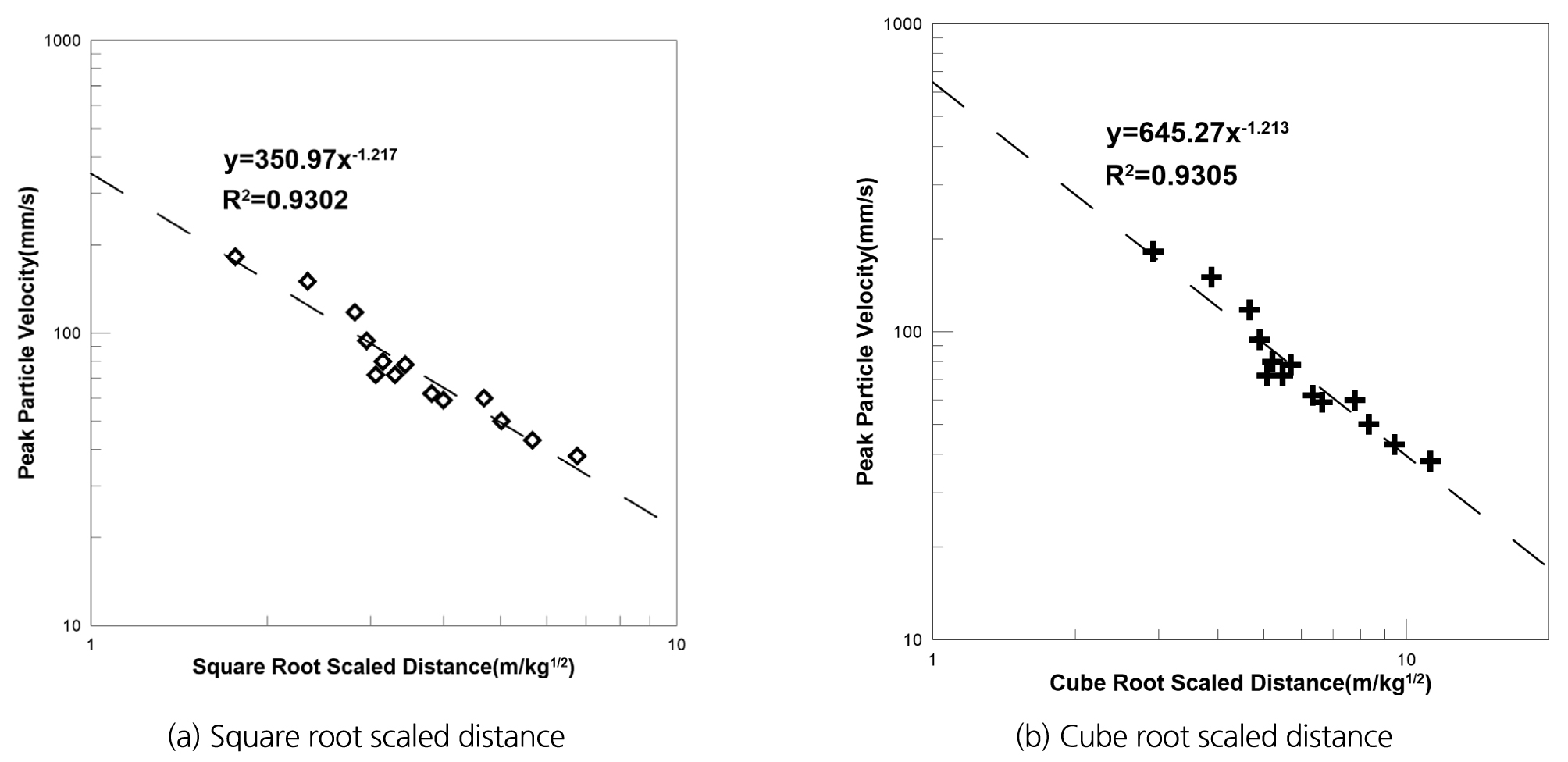
본 연구에서 추정된 자승근 환산거리, 삼승근 환산거리에 의한 통계적 분석결과는 Fig. 8과 같으며, 각 환산거리에 대한 추정식은 식 (5)와 식 (6)과 같다.
| $$y=350.97(x)^{-1.217\;\;\;\;\;\;\;(R^2=0.9302)}$$ | (5) |
| $$y=645.27(x)^{-1.213\;\;\;\;\;\;\;(R^2=0.9305)}$$ | (6) |
일반적으로 환산거리가 짧은 거리에서는 삼승근 환산거리가, 먼 거리에서는 자승근 환산거리가 잘 맞는 것으로 보고되고 있다(Jeon et al., 2007). 본 연구에서의 발파진동 측정지점은 환산거리가 30 m 이하의 짧은 경우에 해당되기 때문에, 삼승근 환산거리에 의한 추정식을 입력진동파형의 산정에 이용하였다.
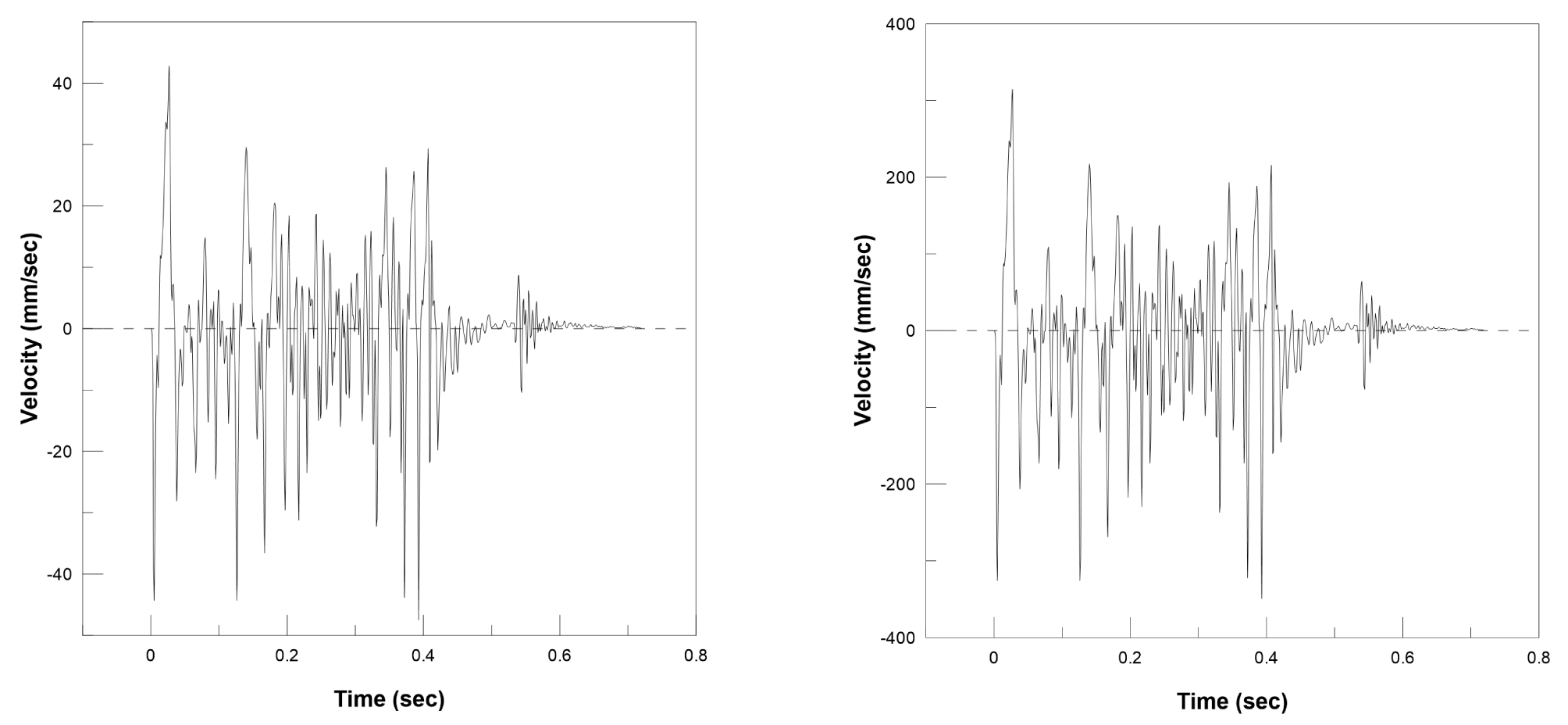
Fig. 9(a)는 발파지점으로부터 20 m 떨어진 지점에서 측정된 수직 성분의 발파진동이며, Fig. 9(b)는 삼승근 환산거리에 의한 추정식을 이용하여 발파지점으로부터 5 m 이격된 지점의 진동파형을 산정한 결과이다. 발파지점으로부터 5 m 이격된 지점에서의 발파진동은 20 m 이격된 지점에 비해 약 7.3 배 크기의 발파진동을 가지며, 추정된 발파진동파형을 동적수치해석의 입력 자료로 이용하였다.
4. 동적수치해석 기법을 이용한 갱내채광장의 안정성 평가
본 연구에서는 발파에 의한 갱내 채광작업이 채굴공동과 안전광주에 미치는 영향을 분석하기 위하여, Kim et al.(2015)에 의해 개발되어 연구대상 광산에 적용하고 있는 주방식 하이브리드 채광법을 모사한 수치해석을 진행하였으며, 앞서 추정된 갱내 채굴공동의 실측진동파형을 수치해석의 입력 자료로 이용하였다.
본 연구대상 지역은 현장조사에서 분석된 바와 같이, 70 ° 이상의 급경사를 갖는 절리군들의 분산도가 매우 낮고, 절리군들이 서로 직교하는 형태를 나타내기 때문에, 절리군의 특성을 강조하여 반영할 수 있는 불연속체 개별요소해석 프로그램인 UDEC을 이용하였다.
채굴공동의 상하좌우 경계면에 시간에 대한 발파진동파형을 채굴공동의 반대 방향으로 입력하여 발파에 의한 동적하중을 모사하였으며, 진동파형의 지속시간까지 해석을 진행하였다.
주방식 하이브리드 채광법을 모사한 동적수치해석에 앞서, 동적수치해석의 입력파형을 추정하는 방법에 따른 적정성을 검토하기 위하여 실제로 발파진동을 계측하였던 갱내 채굴공동을 모사하고, 이론적 및 경험식을 이용한 발파압력이력곡선과 실측진동파형으로부터 추정된 발파진동을 입력 자료로 적용하여 예비 동적수치해석을 수행하였으며, 동일한 지점에서의 실제 발파진동 측정값과 예비해석의 발파진동 측정값들을 비교하였다. 또한 예비수치 해석의 결과로부터 검증된 입력파형을 반영하여 주방식 하이브리드 채광법의 채광순서를 고려한 동적수치해석을 수행하였으며, 해석결과를 종합적으로 분석하여 채굴공동의 안정성을 평가하였다.
4.1 수치모델 및 해석조건
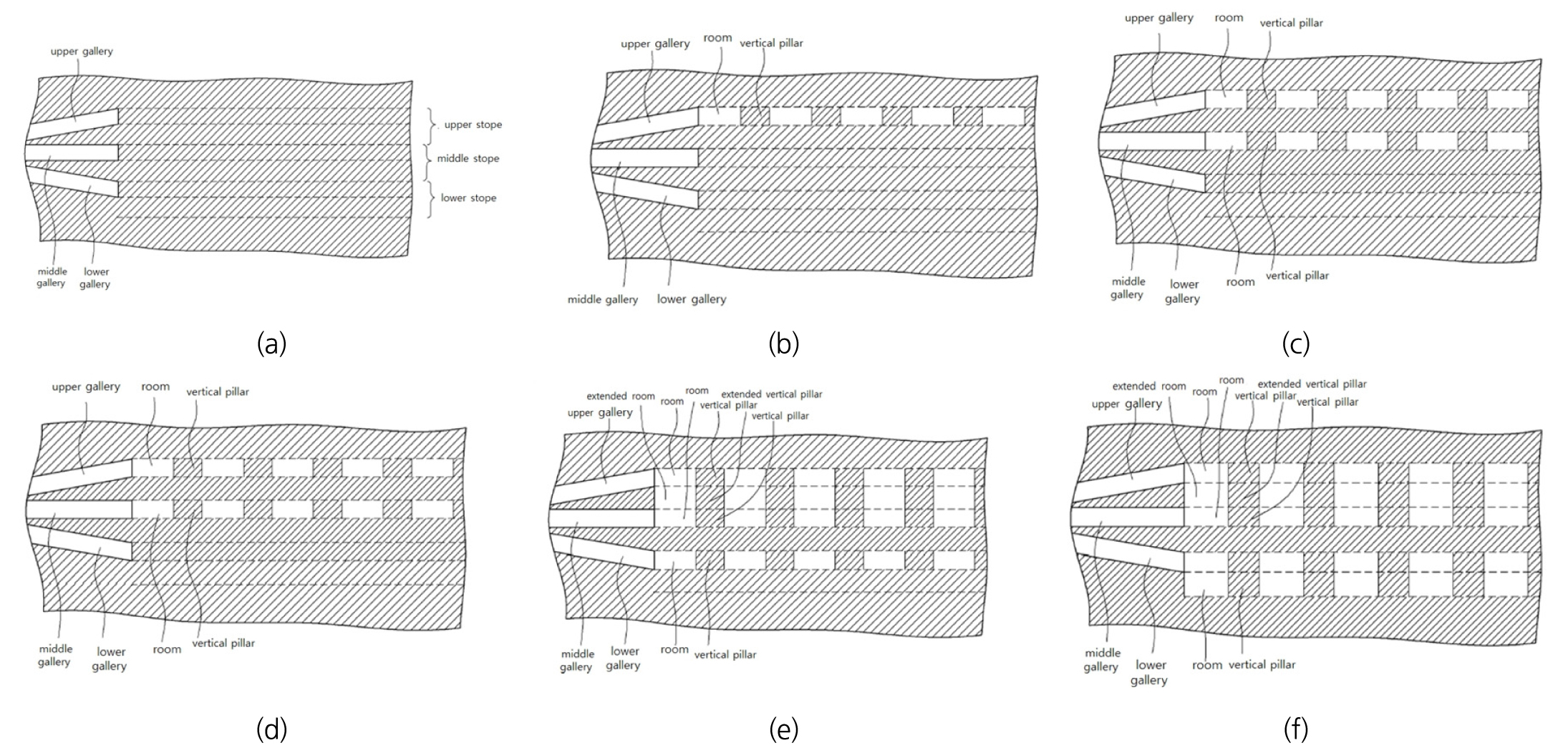
본 연구대상 광산에서 적용하고 있는 주방식 하이브리드 채광법은 채굴공동의 상반을 지지하기 광주를 규칙적으로 남기는 주방식 채광법의 채수율이 낮은 문제점을 해결하고자 Kim et al.(2015)이 제안한 방법이다. 본 채광법은 Fig. 10과 같이, 상부, 중앙, 하부지역의 갱도를 형성하는 단계, 상부 및 중앙의 광석 채광단계, 상부와 중앙의 채굴공동 사이의 수평광주 채광단계, 하부 광석의 채광단계 그리고 하부 채굴공동 하부의 추가 채광단계 순으로 수행되며, 순서는 광산의 상황에 따라 일부 변경되어 적용될 수 있다.
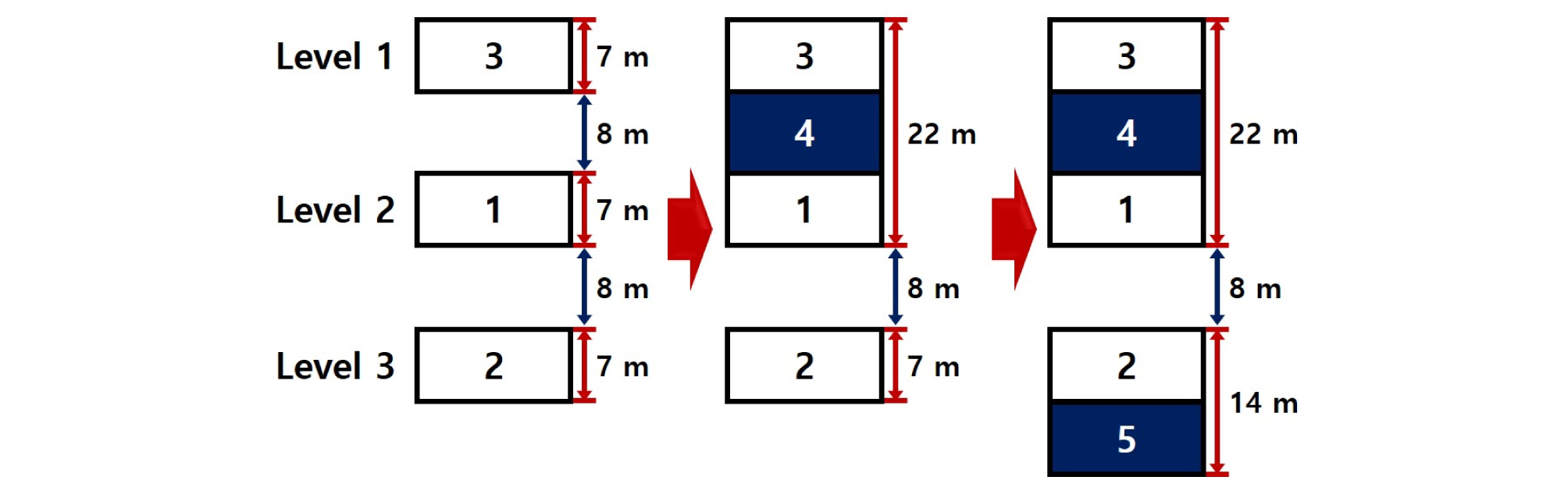
본 연구대상 광산에서 적용되고 있는 주방식 하이브리드 채광법의 채광순서는 Fig. 11과 같으며, 연구대상 광산의 장기적인 안정성 유지를 위해서는 중앙과 하부 채굴공동 사이의 수평 안전광주와 약 22 m 높이를 갖는 수직 안전광주의 역학적 거동특성이 정밀하게 검토되어야 한다.
본 연구에서의 동하중에 의한 안정성 해석은 입력자료의 적정성을 검증하기 위한 예비 수치모델의 해석과 주방식 하이브리드 채광법을 모사한 해석으로 구분되며, 임의로 형성된 경계면에서 나타날 수 있는 진동파의 반사에 의한 영향을 방지하기 위하여 좌우 및 하단의 경계부에 무한 경계조건을 수치모델에 적용하였다.
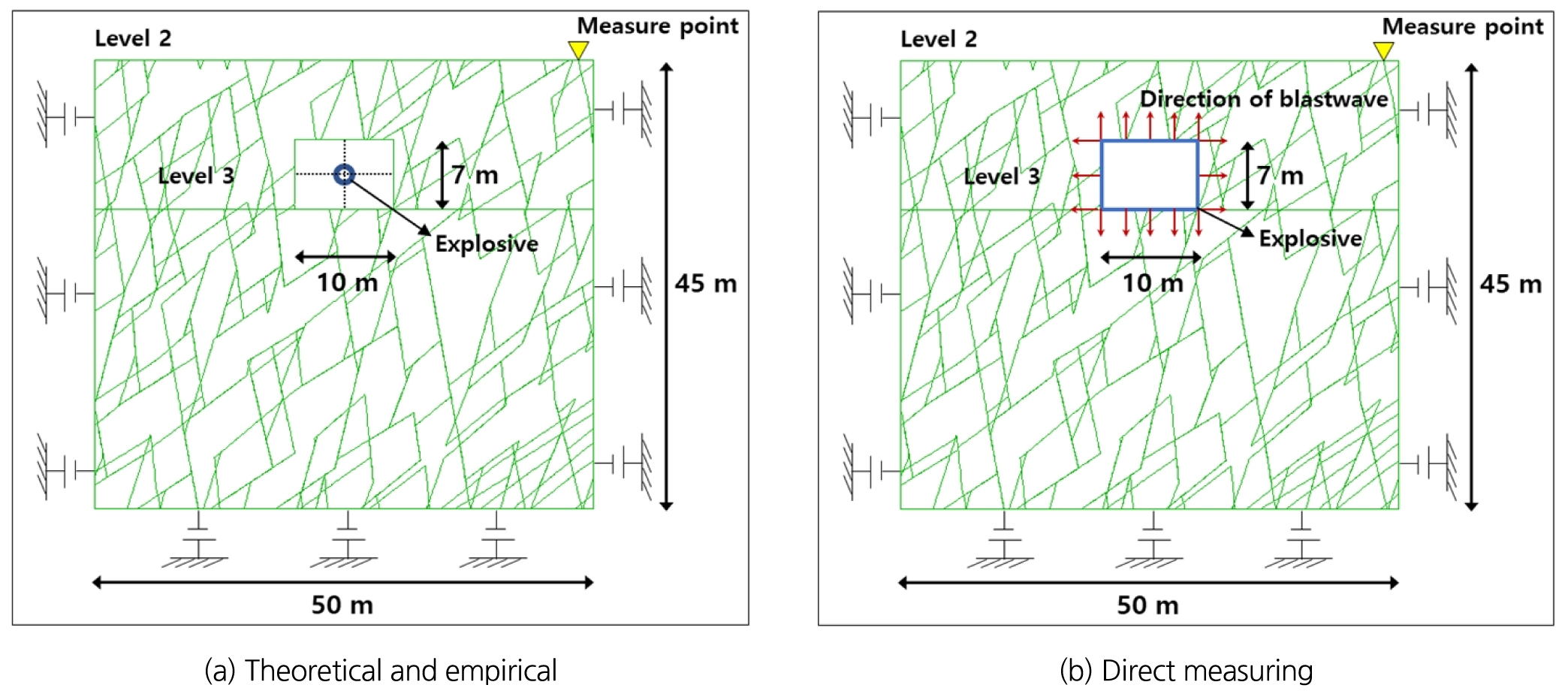
Fig. 12는 예비해석의 수치모델과 해석조건을 나타낸 것이다. 실제 발파진동의 계측이 수행되었던 Level 2와 Level 3을 모사하였으며, Level 3을 발파지점으로, Level 2을 계측지점으로 설정하여 수치모델을 수립하였다. Fig. 12(a)의 이론적 및 경험식을 이용한 발파압력이력곡선을 적용하는 예비해석의 수치모델은 채굴공동의 중앙부분에서 발파압력이 작용하도록 하였으며, Fig. 12(b)의 실측진동파형을 이용한 예비해석의 수치모델은 채굴공동의 최외곽면에서 발파진동이 수평 및 수직방향으로 진행하도록 구성하였다.
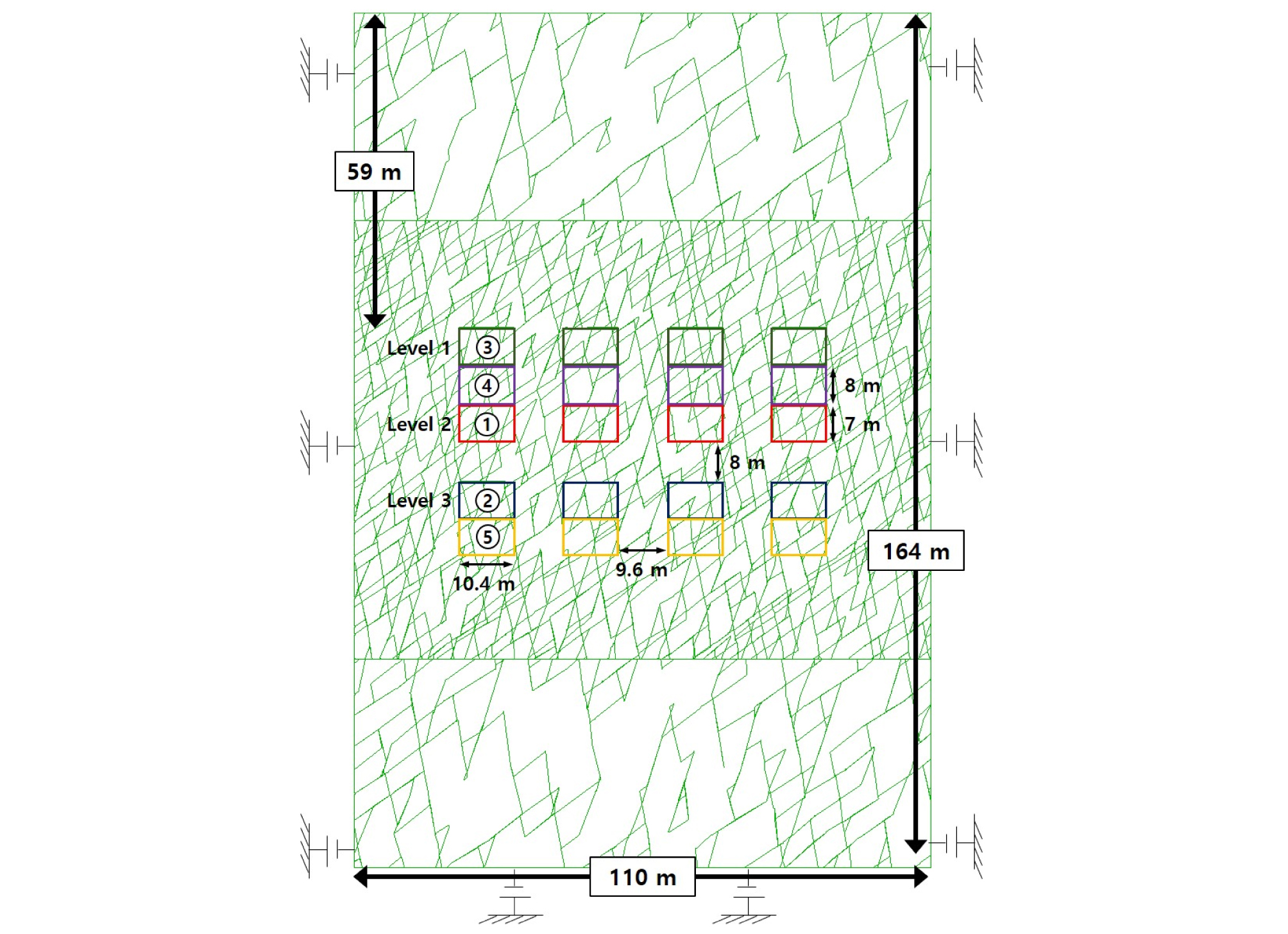
주방식 하이브리드 채광법을 모사한 해석의 수치모델과 해석조건은 Fig. 13과 같으며, 본 연구대상 광산에서 적용하고 있는 채광순서와 현장조사에서 분석된 Level 2 채굴공동의 형상을 직접적으로 반영하여 수치모델을 구성하였다. 수치모델의 중앙에는 84 m의 두께를 갖는 석회석 층이 분포하는 것으로, 석회석 층의 상하부에는 셰일 층이 분포하는 것으로 표현하였으며, 수치모델의 좌우측면에 보안광주를 형성하여 경계효과를 최소화하였다.
현재 연구대상 광산의 Level 2 지역은 채광이 완료된 상태이므로, 이를 반영하여 Level 3 지역부터 채광이 수행되는 것으로 설정하였으며, 현장에서의 발파작업 순서를 고려하여 1번 발파에 1개의 채굴공동을 채광하는 것으로 모사하였다.
절리군의 경사는 동서방향의 해석단면과의 위경사각을 고려한 절리군의 경사를 수치해석에 반영하였다. 또한 절리를 사실적으로 표현하기 위하여 절리의 경사를 표준편차의 범위 내에서 무작위로 부여하였으며, 해석단면의 상하부 영역을 채굴공동 부근의 암반에 2배에 해당하는 절리간격으로 설정하여 해석의 효율성을 고려하였다.
4.2 입력물성 산정
수치해석을 위한 동적입력물성의 산정을 위해 별도의 실내시험을 수행하였으며, 암반과 절리에 대한 정적물성은 동일한 지역의 시추코어를 대상으로 실내시험을 수행한 Kwon et al.(2016)의 결과를 참조하였다(Table 2). 암반의 측압계수 또한 Daesung MDI(2014)의 수압파쇄 시험으로부터 얻어진 현지응력 값을 참고하였으며, 해석단면을 기준으로 측압계수를 환산하여 1.41의 값을 적용하였다.
Table 2. Properties of rock and joint for numerical analysis (Kwon et al., 2016)
암반의 동적물성의 특성을 분석하기 위하여, ASTM에서 제안하고 있는 ASTM C 215시험법에 따라 양단자유 공진주시험(Free-free resonant column test)을 수행하였으며, 공진주파수, 동탄성계수, 동전단계수, 감쇠비 등의 동적물성을 산정하였다.
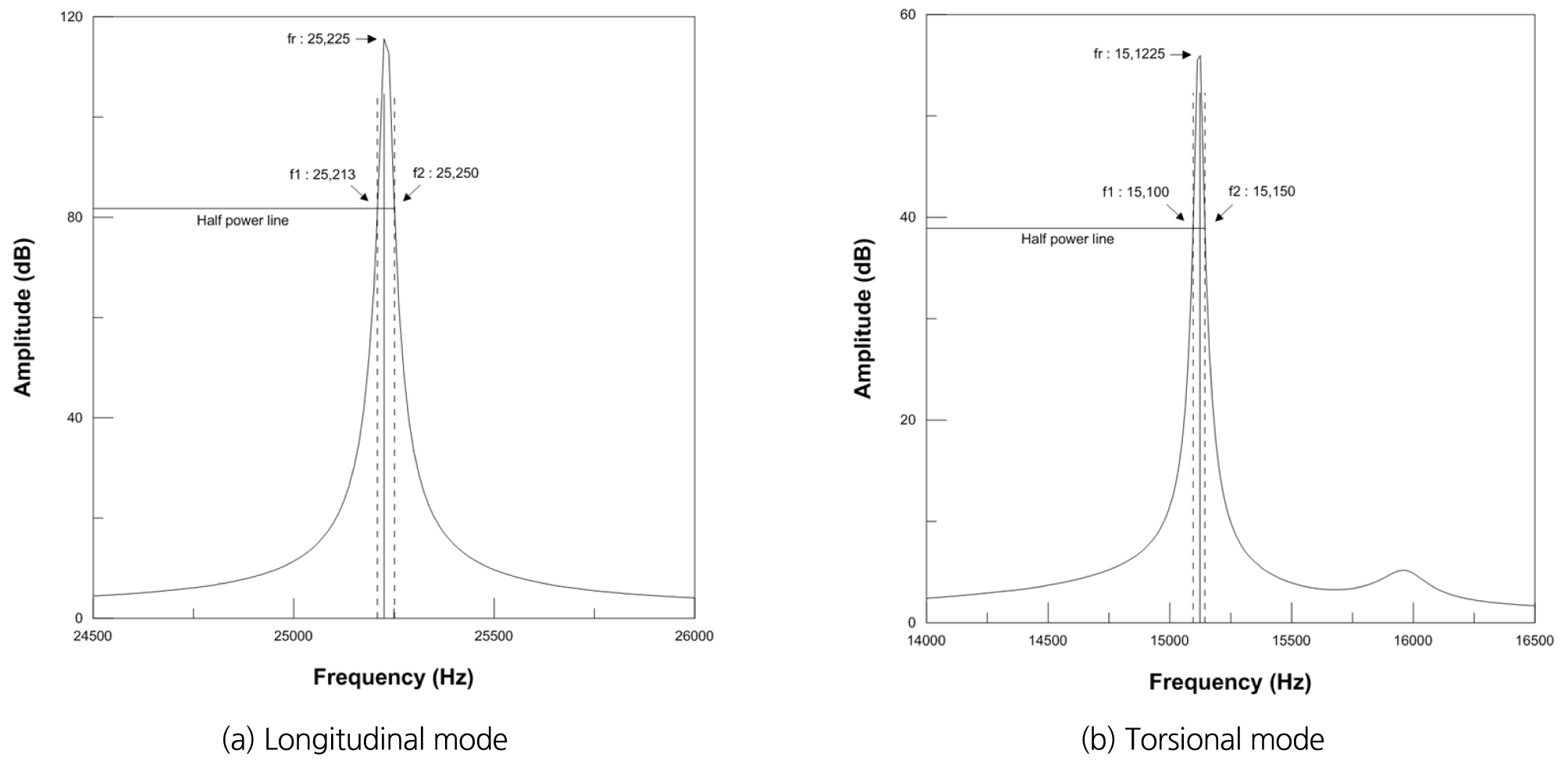
양단자유 공진주시험은 충격반향기법을 이용한 방법으로 충격해머를 이용하여 시편에 길이방향으로 충격을 주고 그 공진주파수(Resonance frequency)를 측정하여 동적물성을 산정하는 방법이다. 시험편에 부착되는 가속도계의 위치와 충격해머의 타격점에 따라 종파 모드(Longitudinal mode)와 비틀림파 모드(Torsional mode)의 공진주파수를 측정할 수 있으며, Fig. 14는 종파 모드의 양단자유 공진주 시험의 전경이다. 양단자유 공진주시험의 감쇠비는 공진주파수에서 진폭의 0.707배에 해당하는 Half-power bandwidth method를 이용하여 산정할 수 있으며, 이로부터 산정된 암석의 동적물성은 Table 3과 같다. Fig. 15는 시험에서 가속도계에 감지된 진폭을 FFT(Fast Fourier Transform)변환하여 주파수 영역으로 표현한 것이다.
본 연구대상 광산의 석회석은 종파 모드에서 24,748 Hz 공진주파수를 가지며, 0.30 %의 감쇠비를 나타낸다. 비틀림파 모드에서의 공진주파수는 14,195 Hz이며, 0.78 %의 감쇠비를 갖는다. 종파는 파동의 진동방향과 매질을 이동하는 진행방향이 일치하기 때문에 비틀림파에 비해 높은 공진주파수와 낮은 감쇠비를 갖는 것으로 분석하였다.
Table 3. Dynamic properties of rock specimens
4.3 해석결과
본 연구에서는 동적수치해석의 입력파형을 추정하는 방법에 따른 진동파형의 전파양상과 적정성을 검증하기 위하여 예비 수치모델의 해석을 수행하고, Fig. 13의 채광순서에 근거하여 주방식 하이브리드 채광법을 모사한 해석을 수행하였다.
채광순서에 근거한 해석은 단계별로 채광이 진행됨에 따른 채굴공동과 광주의 안정성을 검토하기 위하여 변위발생 및 소성영역 분포도, 주응력 분포도를 분석하였으며, 채굴공동과 광주의 불안정성이 확인되는 단계까지 해석을 진행하였다.
4.3.1 예비 수치모델의 해석결과
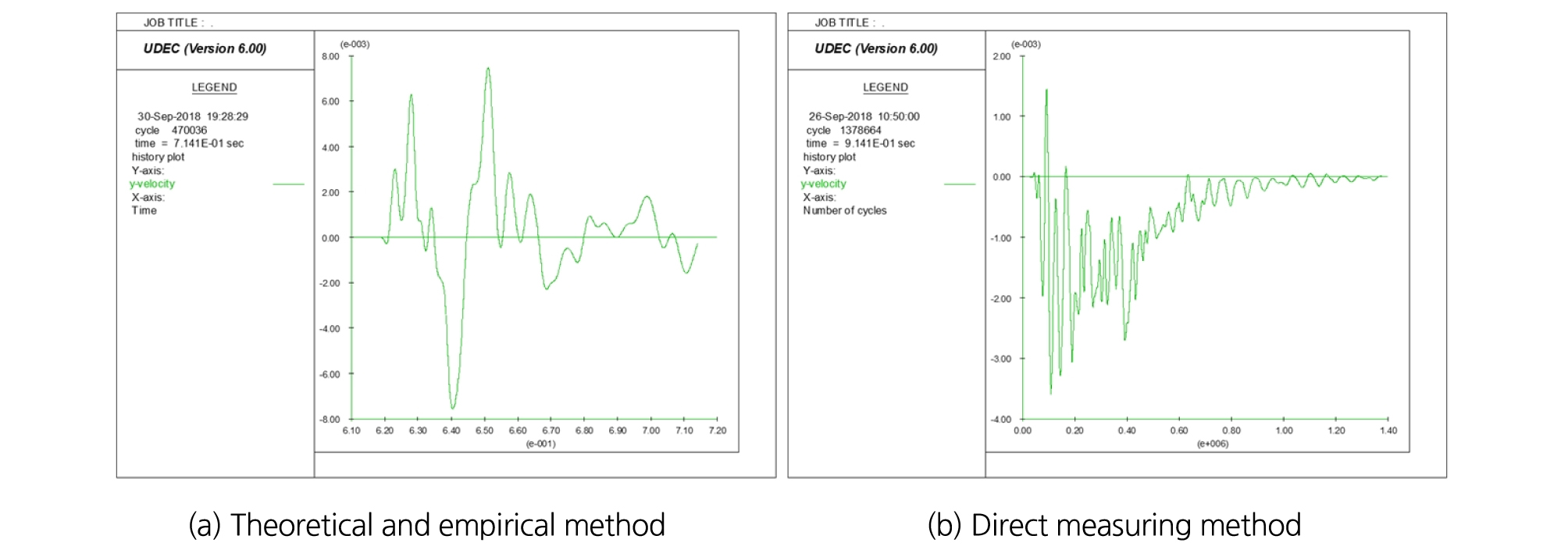
상부 채굴공동인 Level 2의 계측지점에서 측정된 속도벡터의 시간이력은 Fig. 16과 같으며, 실측진동파형을 이용하여 추정하는 방법은 이론적인 계산식 및 경험식을 이용하는 일반적인 방법에 비해 Fig. 9의 현장에서 계측된 진동파형과 유사한 형태를 나타내고 있다.
Table 4는 현장에서 계측된 발파진동 값과 동적수치해석에서 실측발파진동과 이론적 및 경험식에 의한 발파하중을 입력 자료로 이용하여 계측된 발파진동 값을 비교한 결과이다. 20 m 이격된 거리에서 계측된 발파진동의 크기는 이론적 및 경험식에 의한 발파하중을 이용한 해석, 현장에서의 계측, 실측발파진동을 이용한 해석의 순이며, 이론적 및 경험식에 의한 발파하중을 이용한 해석은 다른 두 방법의 발파진동보다 31.78 mm/sec 이상의 큰 차이를 나타내고 있다. 이러한 양상은 동적수치해석의 입력 자료로 이용한 이론적 및 경험식에 의한 발파하중은 현장의 암반 및 절리특성과 지연시차, 발파공법 등의 발파조건을 고려하지 못하기 때문인 것으로 판단된다.
Table 4. Peak particle velocity obtained from field measurement and their applications to dynamic analysis
| Type | Applied method of blast load | Distance from blast (m) | Peak particle velocity (mm/sec) |
| Field measurement | - | 20 | 42.80 |
| Dynamic analysis | Direct measuring | 35.98 | |
| Theoretical and empirical | 74.58 |
또한 실측발파진동을 이용한 해석의 발파진동은 실제 계측된 발파진동에 비해, 6.82 mm/sec 작은 수준을 나타내는 것으로 확인되었으며, 이는 실제의 발파효과에 비하여 다소 불리한 결과를 도출할 수 있음을 의미하나, 실제의 암반과 수치모델에 모사된 암반의 절리분포, 암반의 물성 등을 고려할 때 실측진동파형을 이용하는 방법이 적정한 것으로 판단된다.
이상의 결과를 종합해보았을 때, 현장의 지질특성과 발파조건을 반영하고 있는 실측진동파형을 이용한 발파진동을 입력 자료로 이용하는 것이 이론적 및 경험식에 의한 발파하중을 입력 자료로 사용하는 것에 비해 합리적인 것으로 판단되며, 실측진동파형을 이용한 발파진동을 연구대상 광산의 갱내채광장을 모사한 동적수치해석의 입력 자료로 이용하였다.
4.3.2 갱내채광장의 동적수치해석 결과
본 연구에서는 대상광산의 현장상황이 반영된 갱내채광장의 안정성을 분석하기 위하여 Level 2의 채광이 완료된 광산의 상황을 모사하여 갱내채광장의 수치해석을 수행하였으며, 이후에 예비 수치모델에서 적정성이 검증된 실측진동파형을 적용하여 Level 3의 채광단계별로 동적수치해석을 수행하였다.
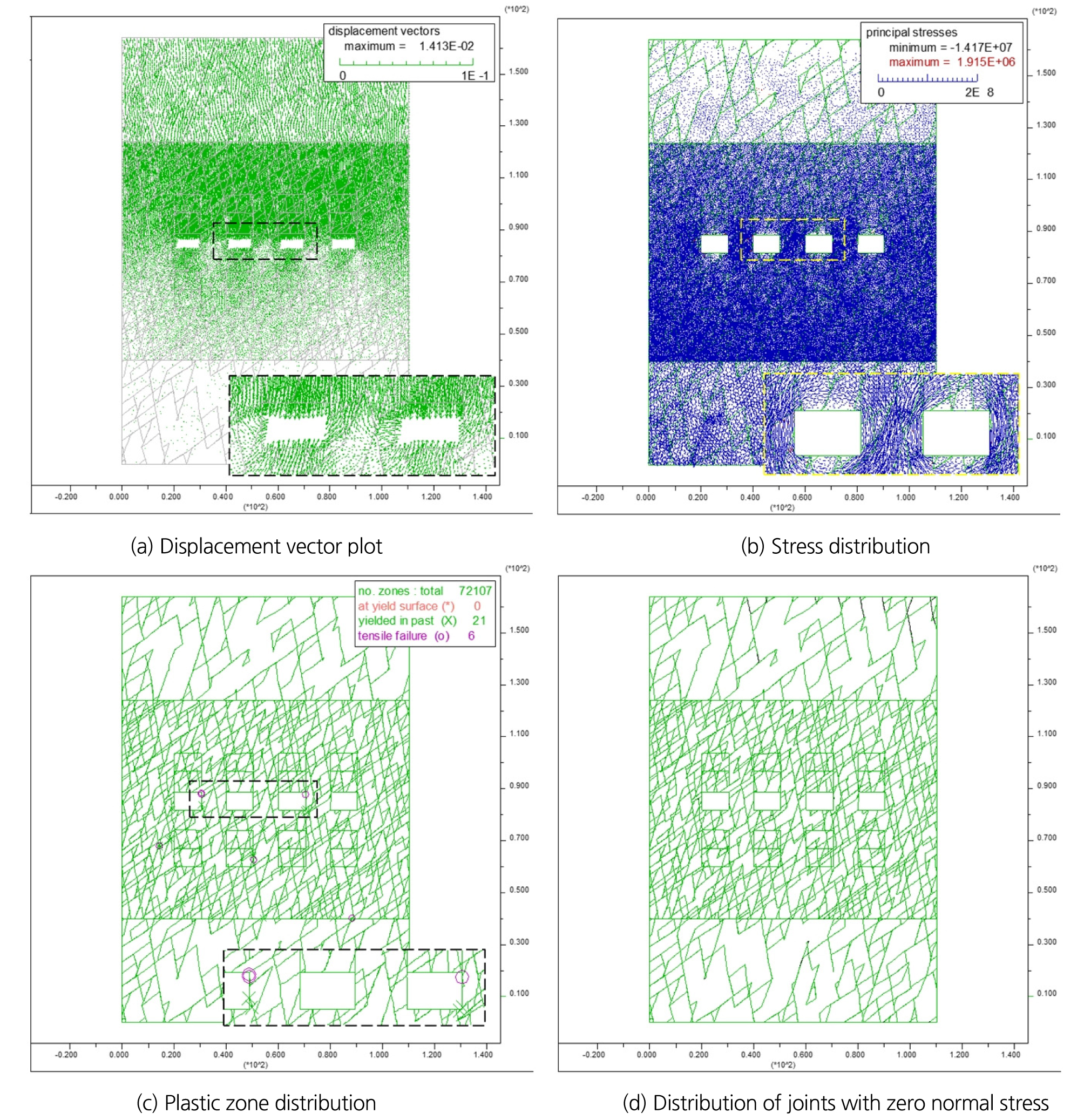
Fig. 17은 Level 2의 채광이 완료된 갱내채광장의 수치해석을 수행한 결과이다. Fig. 17(a)와 Fig. 17(b)의 변위 발생양상 및 응력텐서 분포도에서 보이는 바와 같이, 채굴공동의 천반에서 최대 1.41 cm의 변위를 갖는 소규모 낙반이 발생하는 것으로 나타나고 있으나, 채굴공동 주변의 응력 재분배로 인해 채굴공동 상부의 응력아치를 형성하기 때문에 채굴공동의 안정성은 확보된 것으로 판단된다.
Level 2의 채굴공동 상부에서 소수의 활동성 인장파괴 영역이 관찰되고 있으나, 채굴공동의 주변에서 절리면의 응력이완 현상이 확인되지 않기 때문에, 이는 채광장에 분포하는 절리들에 의해 생성된 암석의 형상에 의한 영향이며, 이로 인하여 채굴공동의 불안정성을 야기하지 않을 것으로 생각된다(Fig. 17(c)와 Fig. 17(d)).
Fig. 17(a)~(d))의 결과로부터 Level 2의 채광이 완료된 채굴공동은 국부적으로 불안정한 요인이 확인되나, 채굴공동의 역학적인 안정성에 영향을 미치지 않는 상태인 것으로 판단된다.
Fig. 18은 Level 3의 2번째 채굴공동의 채광에 대한 동적수치해석 결과이다. Level 3의 1번째 채굴공동의 채광에 대한 동적수치해석 결과는 Level 2의 채광이 완료된 갱내채광장의 수치해석 결과와 유사한 양상을 나타내고 있으므로 별도의 안정성 분석을 수행하지 않았다.
Level 3의 2번째 채광에 대한 변위발생 양상과 응력텐서 분포는 Fig. 18(a)와 Fig. 18(b)과 같다. Level 2의 채굴공동 천반에서 약 4 m의 대형 암괴가 탈락되어 천반이 붕락되는 현상을 관찰할 수 있으며, 붕락된 천반 주변의 암반에서 활동성 인장파괴 영역도 나타나고 있다. 또한 Level 2의 채굴공동과 Level 3의 채굴공동 사이에 존재하는 수평 안전광주에서는 다량의 변위가 확인되지는 않지만, 활동성 인장파괴 영역이 넓은 지역에 걸쳐 다수 분포하는 것으로 보았을 때, 수평 안전광주가 인장파괴에 의해 이완된 상태이나, 수평방향에서 작용하는 측압에 의하여 변위가 억제된 것으로 분석된다.
Fig. 18(c)의 응력텐서 분포도에서 Level 2의 채굴공동 상부에서 응력해방 현상이 확인되고 있으나, 천반이 붕괴된 영역의 상부에 응력아치가 형성되고 있는 것으로 보인다. 이러한 양상은 Fig. 18(d)의 응력이 이완된 절리의 분포도에서도 동일하게 확인할 수 있다. 또한 Level 2의 일부 수직광주에서는 절리의 경사방향으로 응력이 집중되는 양상을 보이며 있으며, 약 8 MPa의 압축응력이 Level 2의 우측에 위치한 수직광주 하부에서 관찰되고 있다. 이러한 응력집중 현상은 안전범위 이내이나, 광주에 분포하는 활동성 인장파괴 영역으로 인하여 채광장의 불안정성이 야기 될 수 있는 것으로 분석된다.
이상의 분석결과로부터 확인할 수 있듯이, Level 3에서의 발파에 의한 채광활동이 채광장의 천반붕락과 수직 및 수평광주의 불안정성을 야기할 수 있을 것으로 판단되며, 지속적인 채광활동을 위해서는 채굴공동의 천반과 광주에 대한 추가 보강 대책이 필요할 것으로 판단된다.
5. 결 론
본 연구에서는 발파진동이 석회석 갱내채광장의 안정성에 미치는 영향을 분석하기 위하여 대상 광산의 암반과 절리의 특성을 조사하였으며, 실측진동파형을 이용하기 위하여 발파현장에서 계측을 수행하고 계측된 진동파형을 발파지점의 진동속도로 변환하였다. 이로부터 변환된 진동속도를 동적수치해석의 입력 자료로 이용하여, 불연속체 기법의 동적수치해석을 수행하였다. 본 연구를 통해 도출된 연구 결과를 정리하면 다음과 같다.
1) 본 연구대상 광산에는 급경사를 갖는 주절리군이 서로 직교하는 형태로 분포하고 있어, 절리의 거동특성에 대한 고려가 필요하고, GSI 및 RMR 분류법을 이용한 암반상태에 대한 평가를 통하여 보통이상의 암반상태를 나타내는 것으로 분석되었다.
2) 동적수치해석에 의한 석회석 갱내채광장의 안정성 평가시 사실적인 발파현상을 모사하기 위하여 연구대상 광산에서 총 6회의 발파를 수행하여 발파진동을 직접적으로 계측하고, 이를 기반으로 진동파형에 관한 삼승근 환산거리의 발파진동 추정식을 y=645.27(x)-1.213와 같이 산정하였다. 이를 이용하여 발파경계면에서의 진동파형을 추정하였으며, 발파경계면에서의 발파진동은 20 m 이격된 계측지점에서의 발파진동에 비해 약 7.3배 증폭된 파형을 갖는 것으로 분석되었다.
3) 동적수치해석의 입력파형을 추정하는 방법에 따른 동적수치해석 결과와 현장에서 계측된 발파진동 값과의 비교를 통하여, 입력파형을 추정하는 방법에 따른 적용성을 검토한 결과, 동적수치해석에서 실측진동파형을 이용하여 추정하는 방법은 이론적 및 경험식을 이용하는 일반적인 방법에 비해 현장에서 계측된 발파진동 파형과 유사한 형태를 나타내고 있으며, 발파진동 값 또한 6.82 mm/sec의 근소한 차이를 갖는 것으로 확인되었다. 이는 기존의 이론적 및 경험식을 이용하는 방법이 현장의 암반 및 절리특성과 발파조건을 고려하지 못하는데 반해, 실측진동파형을 이용하는 방법은 현장 및 발파의 모든 조건이 진동파형에 반영되어 있기 때문이며, 이로부터 실측진동파형을 이용한 발파진동을 동적수치해석의 입력 자료로 사용하는 것이 합리적인 것으로 판단된다.
4) 주방식 하이브리드 채광법을 적용한 대상광산의 안정성을 확인하고자 채광작업으로부터 발생되는 발파진동을 고려한 불연속체 수치해석을 수행하였으며, 채광이 완료된 Level 2의 채광장에서는 소규모의 낙반, 활동성 국부적인 활동성 파괴영역과 같은 불안정한 요인이 확인되고 있으나, 채굴공동 상부의 응력아치가 형성되어 채굴공동의 안정성이 확보된 것으로 판단하였다. 이후 단계에서는 Level 3에서의 발파작업에 의한 채굴공동 천반에서의 대규모 변위발생과 채굴공동의 주변 및 안전광주에 분포하는 활동성 파괴영역의 확장을 관찰할 수 있으며, 이는 발파작업에 의하여 채굴공동 주변과 광주에 안정적으로 형성되었던 응력이 교란되었기 때문인 것으로 분석된다. 이상의 결과들로부터 본 연구대상 광산에서는 발파에 의한 채광활동이 채광장의 불안정성을 야기할 수 있을 것으로 판단되며, 지속적인 채광활동을 위해서는 추가적인 보강 대책이 필요할 것으로 판단된다.
본 연구의 실측진동파형을 이용하여 갱내채광장의 안정성을 평가하는 방법은 암반의 특성과 발파조건을 정확하게 반영할 수 없는 기존의 방법이 갖는 불확실성을 감소시킬 수 있는 것으로 분석되었으며, 이는 높은 안전율이 요구되는 터널 및 지하공간에서의 발파, 기계굴착 등의 동적 하중을 고려한 안정성 분석에 도움이 될 것으로 생각된다.