1. 서 론
2. 배경 이론
2.1 일축압축강도(UCS)와 현장 관입 지수(FPI)
2.2 머신러닝(Machine Learning)
3. 데이터 분석 및 머신러닝 기법 적용
3.1 현장 개요 및 데이터
3.2 머신러닝 회귀기법 적용
4. 분석 결과
5. 결 론
1. 서 론
쉴드 TBM(Tunnel Boring Machine)을 이용한 굴착 공사에서 굴진성능(Performance)은 전체 TBM 공사기간과 공사비 예측에 영향을 미치는 중요한 요소이며, 이를 예측하기 위해 다양한 모델들이 제안되어 왔다. 대표적으로 TBM의 굴진성능을 나타내는 지표로는 관입율(Penetration Rate, PR)과 현장 관입 지수(Field Penetration Index, FPI)가 있다. 굴진성능을 예측하는 대표적인 모델로는 개별 디스크 커터의 작용력을 기반으로 하는 이론적인 CSM 모델(Rostami and Ozdemir, 1993, Rostami, 1997)과 TBM 현장 사례들을 기반으로 하는 경험적인 NTNU 모델(Bruland, 1998, Macias, 2016)이 있고, 이외에도 Gehring(Gehring, 1995), QTBM(Barton, 1999), RME(Bieniawski et al., 2006) 등이 있다. 2000년대 이후의 굴진성능 예측 모델에 대해 Lee et al. (2016)은 26개의 예측 모델을 분석하여 입력인자 선정단계와 예측기법 적용단계에 따라 분류한 바 있다.
한편, 쉴드 TBM의 굴진성능은 TBM 장비의 성능, 운전자(Operator)의 숙련도, 현장 관리 체계, 필요 자재 적시 공급, 유지관리 등에도 영향을 받지만, 무엇보다 굴착 암반의 상태와 같은 지반조건에 큰 영향을 받는다. Lee et al.(2016)는 TBM 굴진성능 예측모델의 입력 및 출력 인자를 정리하여 주요 영향인자의 적용 빈도를 분석하였으며, 이를 상위 5개의 인자로 요약하면 다음의 Table 1과 같다. 사용된 빈도수가 가장 높은 입력인자는 암석의 일축압축강도(Uniaxial Compressive Strength, UCS)이며, 이를 통해 UCS가 가장 중요한 인자임과 동시에 현장의 실무자가 획득하기 쉬운 인자로 그 활용도가 높음을 유추할 수 있다. 하지만, UCS는 굴진 성능을 결정짓는 중요한 요소임에도 불구하고 지반조사 시 실내실험을 통해 얻을 수 있으나, 전체 TBM 굴진 구간에 대해 모두 알 수 없는 한계점이 있다.
따라서 본 연구에서는 TBM 굴착 중 생성되는 기계 데이터와 회귀분석 모델(Regression model)을 기반으로 하는 머신러닝(Machine Learning) 기법을 활용하여 굴진 중 실시간으로 현재 굴착하는 지반에 대한 UCS를 예측할 수 있는 연구를 수행하였다. 이를 통해 TBM의 암반 구간 굴착 시 운전자의 장비 제어에 도움을 주고, 굴진성능 예측 모델링의 최적화 분석을 통한 자동 운전 제어(Auto Steering) 관련 연구 등에 유용할 것으로 판단된다.
Table 1.
Frequency of input parameter for TBM performance prediction (Lee et al., 2016)
2. 배경 이론
2.1 일축압축강도(UCS)와 현장 관입 지수(FPI)
지반조사 단계에서 시추(Boring)를 통해 획득할 수 있는 UCS는 터널이나 지하공간 설계 및 시공에서 중요한 인자 중 하나이다. 앞서 언급한 바와 같이, 쉴드 TBM 굴진 시 암반의 상태는 굴진 성능과 밀접한 관계가 있으나, 지반조사 시 제한적으로 UCS를 얻는 한계점이 있고, 이에 따라 시추공 사이의 구간에 대해 암반 상태의 불확실성 또한 존재한다.
쉴드 TBM 굴진성능이 암반의 강도와 관계있음은 현장 관입 지수(Field Penetration Index, FPI)를 통해 설명할 수 있다. FPI는 일반적으로 암반에서 절삭기의 성능을 설명하는데 사용되며, 쉴드 TBM에 적용하면 아래 식 (1)에서 볼 수 있듯이 굴진 추력과 TBM 커터의 개수에 따른 관입율로 정의될 수 있다. 여기서, Fn은 TBM 커터 당 추력으로 kN/cutter 이고, Prev는 커터 회전당 관입깊이로 mm/rev표현되며, FPI는 Fn을 Prev으로 나눈 값으로 (kN/cutters)/(mm/rev)로 나타낼 수 있다.
| $$FPI=\frac{F_n}{P_{rev}}$$ | (1) |
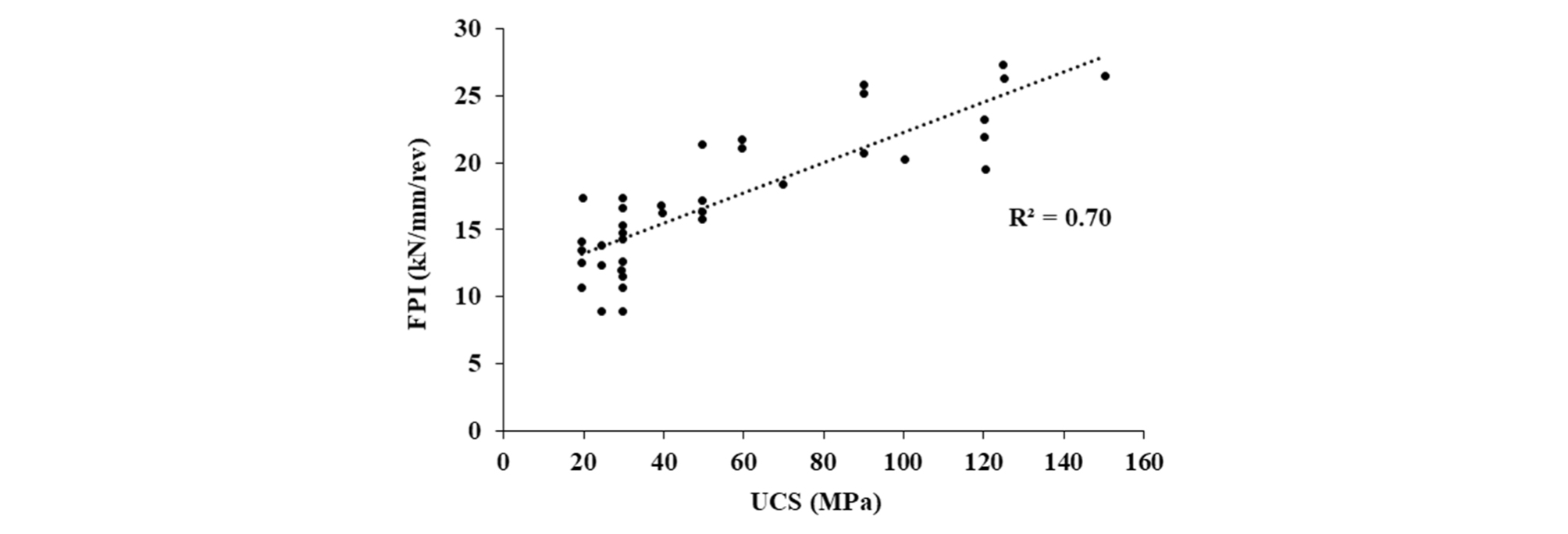
Hamidi and Bejari(2013)가 암반분류법인 RMR 시스템에 이용되는 여섯 가지 인자 중 다섯 가지인 일축압축강도, 암질 계수(RDQ), 절리의 간격, 절리의 상태, 지하수에 대해 FPI와 관계를 분석한 결과는 Table 2와 같으며, UCS가 다른 인자들에 비해 높은 상관관계를 가지는 것을 확인하였다. 또한 아래 Fig. 1에서 볼 수 있듯이 FPI와 선형 관계를 가지는 것을 알 수 있고, 이를 통해, 암반의 강도와 쉴드 TBM 굴진성능이 밀접한 관계가 있음을 확인할 수 있다.
Table 2.
Correlation of FPI with RMR input parameters (Hamidi and Bejari, 2013)
| RMR five input parameters | R2 value | |
| 1 | UCS | 0.70 |
| 2 | Joint spacing | 0.62 |
| 3 | RQD | 0.59 |
| 4 | Partial rating of joint conditions | 0.45 |
| 5 | Partial rating of groundwater conditions | 0.04 |
2.2 머신러닝(Machine Learning)
인공지능의 한 분야로 머신러닝(Machine Learning) 및 딥러닝(Deep Learning)은 여러 분야에 활발히 활용되고 있으며, 학술적으로는 딥러닝은 머신러닝의 한 종류이다. 머신러닝은 지도학습(Supervised Learning), 비지도학습(Unsupervised Learning)과 강화학습(Reinforcement Learning) 3 가지로 분류할 수 있으며 목적에 따라 적절한 머신러닝 기법을 적용해야 한다. 지도학습은 입력값과 결과값을 같이 주고 학습을 시키는 방법으로 분류 및 회귀 등 여러 가지 방법에 쓰이므로 본 연구에서는 지도학습의 한 분야인 회귀분석 기법을 사용하였다. 딥러닝(Deep Learning)은 모델이 결과를 내는 방법을 알기 어려운 블랙박스(Black box) 형태라 결과에 대한 설명이 필요한 경우 적합하지 않으며 결과 도출까지의 시간이 오래 걸리므로, 추후 TBM 현장에서 실시간 생성되는 기계 데이터를 분석하여 결과를 도출하기에는 어려움이 있다고 판단되어 분석기법에서 제외하였다. 본 연구에서는 여러 회귀모델을 사용하여 비교 평가하였고, 각 회귀모델에 대한 개략적인 내용은 다음의 Table 3과 같다.
Table 3.
Summary of the machine learning models used in this study
2.2.1 규제(Regularization) 모델
일반적인 선형 모델에서 비용 함수(Cost function)는 실제 값과 예측값의 차이인 잔차 제곱합(Residual Sum of Squares, RSS)을 최소화하는 것만 고려한다. 이 경우, 학습 데이터에 지나치게 맞추게 되고, 회귀 계수가 쉽게 커져 오히려 변동성이 심해지고 예측 성능이 저하되기 쉽다. 따라서 비용 함수는 RSS 최소화 방법과 과적합을 방지하기 위해 회귀 계수 값이 커지지 않도록 하는 방법이 서로 균형을 이루어야 한다. 이를 위해 비용 함수에 alpha라는 튜닝 파라미터로 페널티를 부여해 회귀 계수 값의 크기를 감소시켜 과적합을 개선하는 방식을 규제(Regularization)라고 한다. 규제는 크게 L2와 L1으로 구분되며, 이는 각각 Ridge와 Lasso 회귀라고 한다. 본 연구에서는 두 회귀 방법에 대해 alpha값을 조정하여 적합한 모델로 UCS를 예측하였다.
2.2.2 서포트 벡터 머신(Support Vector Machine, SVM)
SVM은 Cortes and Vapnik (1995)에 의해 소개된 이후 앙상블이나 신경망이 대두되기 전 수학적으로 정의가 잘 된 모델로 인기를 끌었다. 비선형 문제에 대해서는 커널 함수(Kernel function)를 이용하여 평면에서 고차원 공간에 사상시킨 뒤 분류하는데, 커널 함수 종류에는 대표적으로 Polynomial, Sigmoid, RBF(Radial Basis Function)이 있다. SVM은 학습 데이터의 분류문제 예측에 사용이 되지만 임의의 실수값을 예측 가능하도록 ε-무감도 손실함수(ε-insensitive loss function)를 도입하여 회귀 문제에도 적용이 가능하며, 이를 SVR(Support Vector Regression)이라고 한다(Vapnik et al., 1996). 본 연구에서는 비교적 성능이 뛰어나다고 알려진 RBF 커널 함수를 사용하여 UCS를 예측하였다.
2.2.3 앙상블 학습(Ensemble learning) 모델
앙상블 학습은 여러 예측기를 생성하고 그 예측을 결합함으로써 보다 정확한 최종 예측을 도출하는 기법이다. 앙상블 학습의 유형은 보팅(Voting), 배깅(Bagging), 부스팅(Boosting)의 세 가지로 나눌 수 있으며, 이외에도 스태킹(Stacking)을 포함한 다양한 앙상블 학습 방법이 있다. 부스팅은 여러 개의 예측기가 순차적으로 학습을 수행하되, 앞에서 학습한 예측기가 예측이 틀린 데이터에 대해서는 올바르게 예측할 수 있도록 다음 예측기에게는 가중치(weight)를 부여하면서 학습과 예측을 진행하는 것이다. 예측 성능이 뛰어나 앙상블 학습을 주도하고 있으며 대표적으로 GBM(Gradient Boosting Machine), XGBoost(eXtra Gradient Boosting), LightGBM(Light Gradient Boosting Machine)이 있다. 스태킹은 여러 가지 다른 서브 모델(Sub model)의 예측 결과값을 다시 학습 데이터로 만들어서 다른 모델인 메타 모델(Meta model)로 재학습시켜 결과를 예측하는 방법으로 앙상블 모델에서도 단일 모델보다 예측 성능이 좋다고 알려져 있다. 본 연구에서는 회귀분석에서 예측 성능이 좋아 앙상블 학습을 주도하고 있는 XGBoost, LightGBM와 스태킹 모델을 사용하였으며, Table 2에서 확인할 수 있듯이, 스태킹의 서브 모델로는 Multiple Linear, Ridge, Lasso, SVR, XGBoost, LightGBM을 사용하였다.
3. 데이터 분석 및 머신러닝 기법 적용
3.1 현장 개요 및 데이터
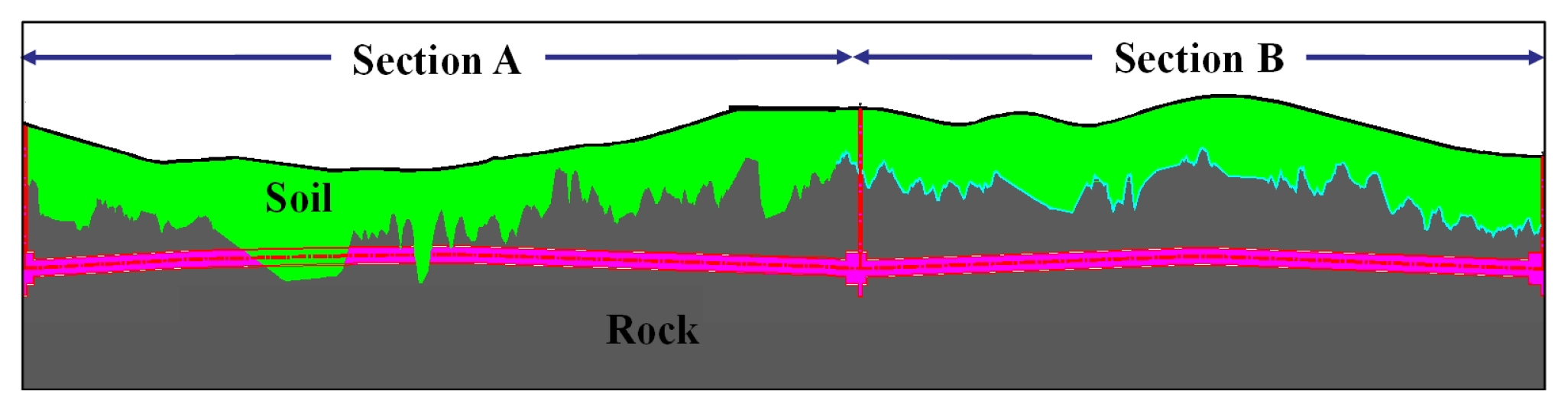
본 연구에서 분석한 slurry 쉴드 TBM 현장의 개략적인 지질 분포는 Fig. 2와 같다. 터널 통과 구간이 대부분 화강암으로 이루어져 있고, 구역 A, B으로 나뉘지만 동일 사양의 slurry 쉴드 TBM 2대가 사용되었다. 사용된 쉴드 TBM의 제원은 Table 4와 같다.
Table 4.
Summary of slurry TBM specification
| TBM type | Slurry |
| TBM outside diameter (mm) | 6,900 |
| TBM length (mm) | 11,650 |
| Max. shield jack thrust force (kN) | 51,200 (1,600 × 32 shield jack) |
| Max. cutterhead torque (kN・m) | 6,250 |
| Max. RPM | 6 |
구간 A는 전체 연장 3.16 km이며 이 중 화강암 구간은 2.72 km이며, 구간 B는 전체 연장 2.23 km 중 화강암 구간은 2.21 km이다. 토피고는 대략 30 ~ 60 m 사이이며, 지하수위는 지표면 아래 5 m로 작용하는 수압은 4 ~ 6 bar 사이이다.
쉴드 TBM으로부터 수집목적에 따라 다양한 형태로 기계 데이터를 추출할 수 있다. 본 연구에서는 생성된 쉴드 TBM 데이터 중 약 5분 간격으로 로그된 데이터를 사용하였으며, 데이터 분석 시에는 실제 TBM이 구동모드인 것만 추출하여 모델링의 입력값으로 사용하였다. UCS 정보가 존재하는 세그먼트 링에 해당하는 기계데이터만을 사용하였으며, 1링의 길이는 1.4 m이다. 현장에서 얻어진 총 40개의 UCS 값을 모델의 출력값으로 사용하였으며, 세그먼트 1링을 굴착하는 동안은 UCS가 동일하다고 가정하였다. 또한, 굴착 구역 모두 동일한 화강암 암반 구간이지만 Table 5에서 볼 수 있듯이, UCS가 최대 127.1 MPa까지 차이가 나고 평균적으로 85 MPa의 강도를 가지는 것을 알 수 있다.
Table 5.
Summary of uniaxial compressive strength data
| Tunnel section | UCS | |||
| Number of UCS data | Valeu of UCS (MPa) | |||
| Min | Max | Average | ||
| A | 23 | 17.2 | 144.3 | 85.0 |
| B | 17 | 44.0 | 115.1 | 85.1 |
3.2 머신러닝 회귀기법 적용
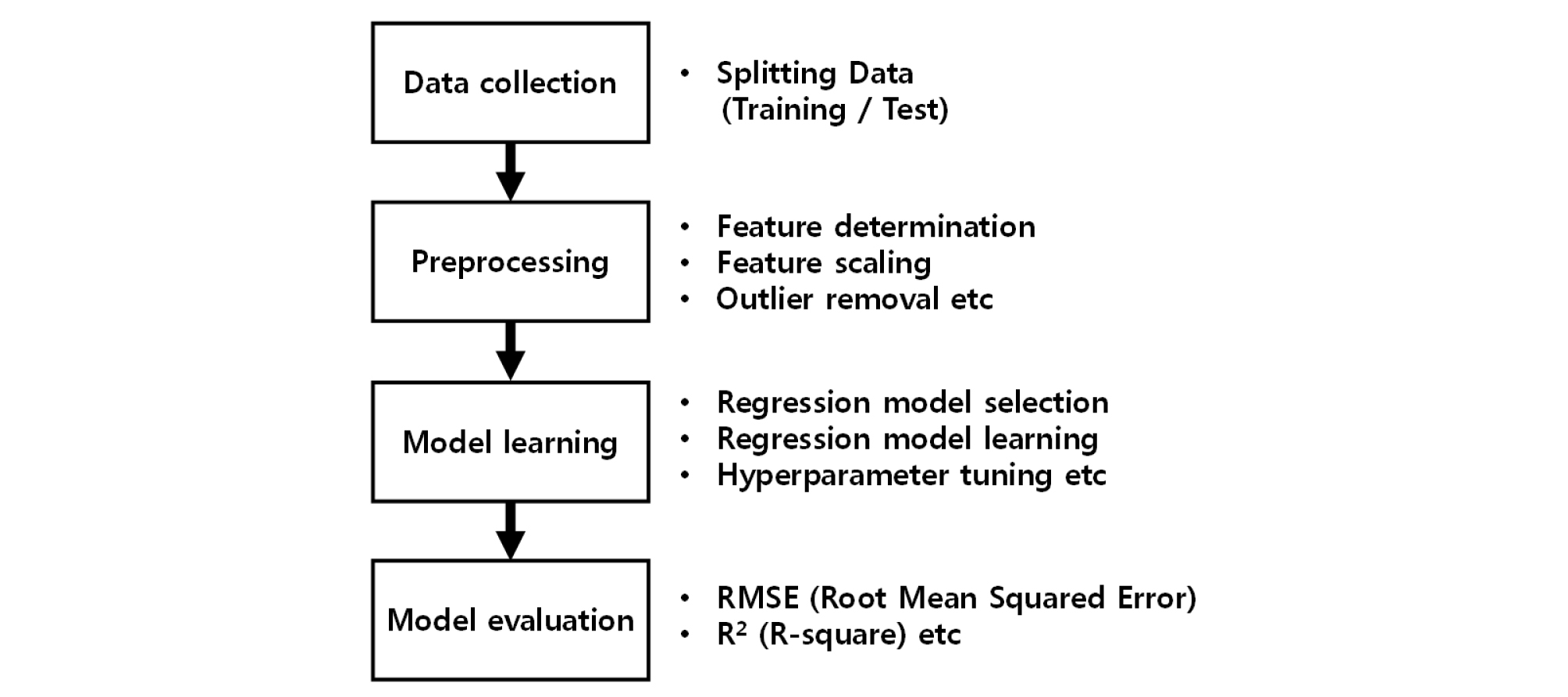
본 절에서는 암반 구간 터널의 기계데이터를 분석하여 UCS를 예측하기 위한 방법을 정립하고자 한다. 머신러닝의 지도학습 기법 중 회귀분석을 위한 알고리즘을 사용하였으며, Python 3.7 버전을 이용하여 분석을 수행하였다. 회귀분석 기법을 적용하는 흐름도는 Fig. 3과 같으며, 적용을 위한 첫 단계는 앞서 3.1절에서 언급한 바와 같이 데이터를 수집한 후, 분석용 데이터와 테스트용 데이터로 분할하여야 하며, 본 연구에서는 8:2의 비율을 사용하였다. Test용으로 분리한 실측 UCS는 예측 UCS와 비교하기 위함이다.
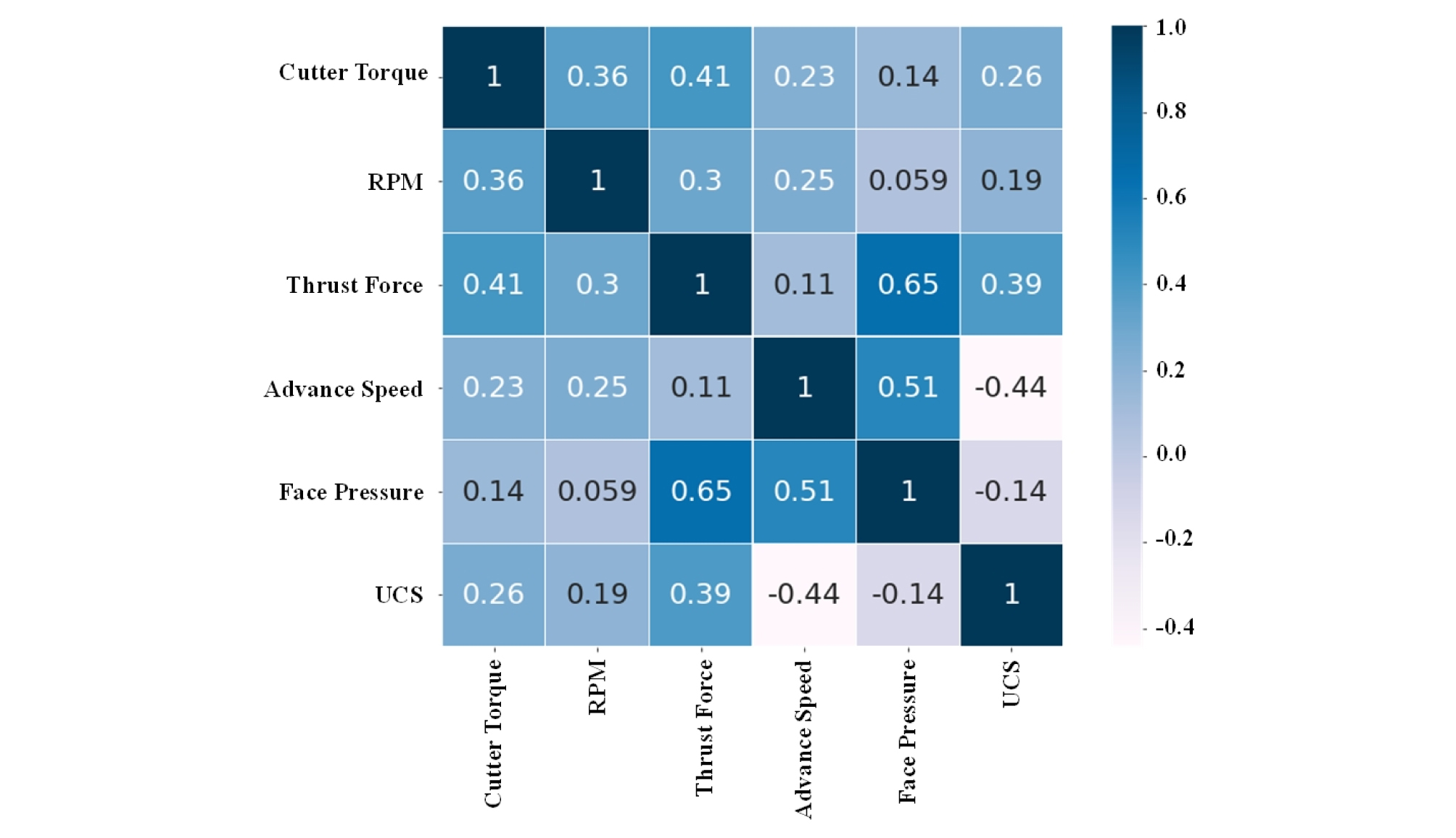
둘째, 전처리(Preprocessing) 과정은 머신러닝 기법 적용에서 매우 중요한 부분이다. 제조사에 따라 상이하지만 본 연구에서는 약 2000개가 넘는 TBM 기계데이터의 특징으로부터 Table 6에서 볼 수 있듯이, 5개로 결정하였으며, 이 특징들은 현재 TBM의 상태를 잘 설명할 수 있는 인자들이다. 결정된 5개의 특징(Feature)과 UCS와의 상관관계를 확인하기 위해 Fig. 4에 나타내었다. 대표적인 양의 상관관계와 음의 상관관계를 분석해보면, 추력(Thrust force)이 가장 높은 양의 상관관계를 보이고 있고, 이는 암석 강도가 증가하면 더 높은 추력이 필요함을 의미한다. 그리고 암석 강도와 굴진 속도(Advance speed)는 음의 상관관계를 가지는 것으로 보아 단단한 암반 구간에서는 굴진 속도가 낮아지는 것을 유추할 수 있다. 각 특징들 간의 유의성은 4절 다중선형회귀 모델을 분석 시 확인하였다.
이상치(Outlier)는 첫째 TBM 장비 상세 사양을 기준으로 제거하였다. 이는 현실적으로 TBM이 수행할 수 없으며, 센서의 이상으로 인해 로깅되는 값들을 제거하는 단계이며, 이런 값들이 포함되어 회귀분석을 실시할 경우 예측력을 떨어트리게 된다. 둘째로 Table 6에서 볼 수 있듯이 표준편차를 이용하여 통계적으로 이상치를 제거하였다. 이상치 제거 후 평균 0, 분산 1로 모든 값의 스케일을 통일시키는 표준화(Standardization)를 적용하였다. 이는 특징 간 스케일이 매우 차이나기 때문에 반드시 수행되어야 하는 단계이다. 세 번째 모델 학습(Model learning)과정에서는 Table 3의 9가지 모델을 통해 학습을 시키되, 각 모델들이 과적합되지 않고, 좋은 성능을 도출하도록 하이퍼파라미터 튜닝(Hyperparameter tuning)을 수행하였으며 이 때 사용되어진 파라미터를 Table 6에 정리하였다. 하이퍼파라미터 튜닝은 각 알고리즘에서 제공하는 툴을 이용해 최적 파라미터를 찾을 수 있으며, 앙상블 학습 모델의 경우 시행착오를 통해 결정할 수 있으므로 분석가 및 데이터에 따라 차이가 있을 수 있다. 마지막으로 모델 평가에서는 실제 오차 값보다 커지는 것을 방지하기 위해 오차 값에 루트를 씌우는 RMSE(Root Mean Squared Error)와 분산 기반으로 예측 성능을 평가하는 결정계수 (R-square, R2)를 사용하였다.
Table 6.
Summary of modelling details
4. 분석 결과
앞서 3절에서 결정된 TBM 특징과 UCS의 상관관계에 대해서 분석하였고, 본 연구에서 학습한 9가지 모델의 성능을 비교하기 전에 먼저 다중선형회귀모델을 분석하고자 한다. TBM의 상태를 잘 설명하는 특징(Feature)으로 결정한 독립변수 간의 유의성을 확인하기 위함이다. 일반적으로 회귀모형의 통계적 검정을 위해서는 유의확률(P-value)이 0.05보다 작아야 한다. 또한, 일반적으로 독립변수들의 상관관계를 의미하는 다중공선성(Multicollinearity)을 표현하는 분산팽창요인(Variance inflation factors, VIF)은 10보다 작아야 한다. 개발한 다중선형회귀 모델의 유의확률은 0.0023이며, Table 7을 보면, 5개의 독립변수들의 분산팽창요인이 10이하로 다중공선성 기준에 위배되지 않으므로 인자 간의 상관관계가 낮음을 확인할 수 있다.
Table 7.
Summary of the VIF factors of multiple linear regression model
| Features | VIF Factors |
| Cutter torque | 1.48 |
| RPM | 1.39 |
| Thrust Force | 3.08 |
| Advance Speed | 2.04 |
| Face Pressure | 3.38 |
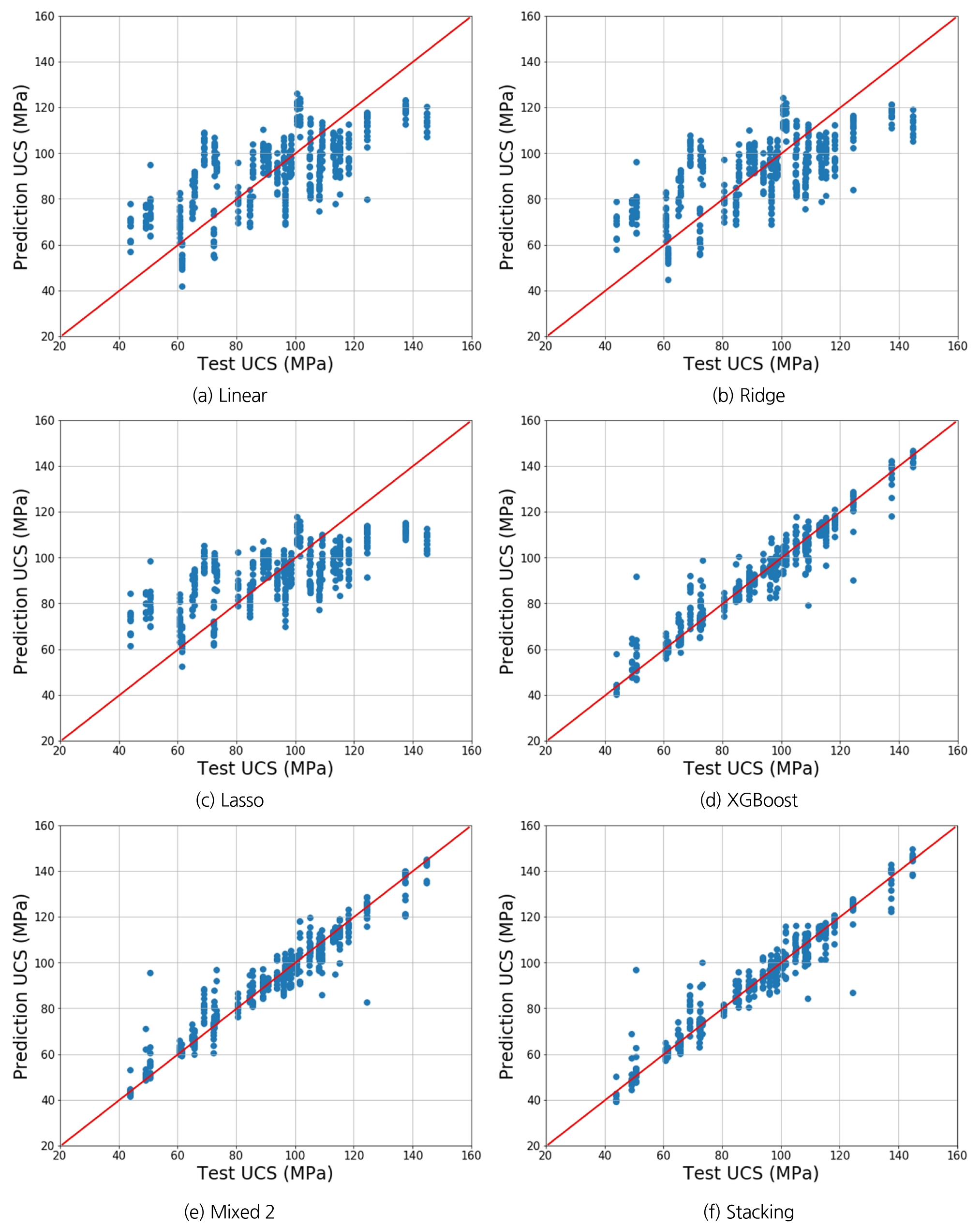
회귀분석 모델로 선정된 9가지를 이용하여 RMSE와 R2에 근거하여 분석한 결과를 Table 8과 Fig. 5에 나타내었고, 예측 결과의 경향에 따라 A와 B 그룹으로 나누어 기술하였다.
앞서 3.2절에서 기술한 바와 같이, RMSE는 오차 값을 나타내므로 작을수록 오차가 적다는 것을 의미한다. Table 8의 그룹 A를 보면 다중선형, Ridge, Lasso, Mixed 1 모델은 RMSE 값이 17.1 ~ 17.6 정도로 나타나고 있으며 결정 계수 또한 0.5에 미치지 못해 모델의 예측력이 좋다고 말하기 어렵다. 또한 모델 학습 시 사용되지 않은 실측 Test용 UCS와 예측한 UCS를 비교 도시화한 Fig. 5의 (a), (b), (c)를 보면 예측이 잘 되지 않은 것을 확인할 수 있다. 이는 UCS 값에 따라 TBM의 기계데이터가 비선형적이고 복잡한 거동을 보이고 있으므로 일반적인 선형 회귀분석을 근거한 모델로는 예측에 어려움이 있다고 판단된다.
Table 8 그룹 B의 RMSE의 경우 A에 비해 현저히 낮은 5.6 ~ 8.5 정도로 도출되었으며, LightGBM을 제외한 모델들의 결정계수 또한 0.9 이상이고, Test용 UCS와 예측 UCS를 도시화하여 비교한 Fig. 5의 (d), (e), (f)를 보면 예측력이 높은 것을 확인할 수 있다. 그룹 B 모델들 중 스태킹 모델은 현실 모델에서는 잘 사용하지 않는 편이나, 적용 분야에 따라 조금이라도 예측 성능을 높이기 위해 적용하는 기법이다. 분석 결과에서 알 수 있듯이 스태킹 모델은 상대적으로 예측 성능이 좋은 그룹 B의 다른 모델들보다도 조금 더 높은 수준의 예측력을 가지는 것을 알 수 있으므로, 최종적으로 스태킹 모델이 UCS를 예측하는데 가장 적합하다고 판단된다.
Table 8.
Results of regression modelling evaluation
본 연구에서 제안한 예측모델을 통해 암반 구간을 굴착하는 쉴드 TBM의 실시간 기계데이터로 UCS 예측이 가능할 것으로 판단되며, 이에 따라 TBM 운전자는 추력 혹은 쉴드 잭 압력과 커터헤드 회전속도인 RPM 등을 조절하는데 유용할 것으로 판단된다. 추가적으로 UCS는 굴진성능을 예측하기 위해 사용되는 필수 인자이므로, 굴진성능 예측 모델링의 최적화 분석을 통한 자동 운전 제어(Auto Steering) 관련 연구 등에 유용할 것으로 판단된다.
5. 결 론
본 연구에서는 쉴드 TBM 기계데이터를 분석하여 굴진성능 도출 시 가장 대표적으로 활용되는 UCS를 예측하였다. UCS를 예측하기 위해 머신러닝의 회귀분석 기법을 사용하였으며, 적용 과정을 정립하였다. 또한 여러 알고리즘의 비교 평가를 통해 가장 예측력이 좋은 모델을 제안하였다. 이 과정을 통하여 도출한 결론 및 요약은 다음과 같다.
1) TBM 기계데이터로 UCS를 예측하기 위한 머신러닝 적용 과정을 데이터 수집부터 전처리 과정, 모델 학습을 포함하여 모델 평가까지 상세히 정립하였다.
2) 선형에 근거하는 회귀분석 모델을 통해 UCS를 분석하면 실측값과 예측값의 RMSE 오차가 17.1~17.6로 형성되고, 결정계수가 0.5 이하로 도출되어 예측력이 약하다. 이를 통해 쉴드 TBM 기계데이터와 암석 강도 간에는 비선형적이고, 복잡한 관계가 있으므로 선형성을 기반으로 한 회귀분석 기법으로는 예측이 불가함을 확인하였다.
3) SVM과 앙상블 학습을 기반으로 하는 모델로 UCS를 분석하면 실측과 예측값의 오차가 5.6~8.5로 형성되고, LightGBM을 제외한 모델들의 결정계수가 0.9 이상으로 도출되어 예측력이 강함을 확인하였으며, 모델 중 스태킹 기법이 가장 예측 성능이 좋음을 확인하였다.
4) 최종 제안된 스태킹 모델은 암반 구간 굴착 시, 쉴드 TBM 운전자에게 제공되어 운전 제어에 도움을 줄 것으로 판단되고, UCS는 굴진성능을 예측하기 위한 필수 인자이므로 굴진성능 예측 모델링의 최적화 분석을 통한 자동 운전 제어 연구에도 유용하게 활용될 것으로 판단된다.