1. 서 론
2. Slip-line법을 이용한 응력분포 계산 원리
2.1 slip-line의 개념
2.2 Slip-line 방정식
3. V형 암석노치의 파괴하중 계산 원리
3.1 해석모델
3.2 불변량 관계식을 이용한 경계응력 결정
4. 암석노치 각도와 경계면 마찰특성에 따른 노치 파괴하중 변화
4.1 노치의 파괴하중 계산식
4.2 노치 각도 변화와 파괴하중
4.3 노치 면의 마찰 특성 변화와 파괴하중
5. 결 론
1. 서 론
Slip-line 해석법은 소성영역 내에서 평형조건식(equilibrium equation)과 항복조건식(yield criterion)을 동시에 만족하는 응력분포를 해석적으로 계산하는 소성해석법의 일종이다. Slip-line법으로 구한 해는 평형방정식, 항복조건식, 응력 경계조건을 모두 만족시킨다는 측면에서 소성해석 이론의 하계정리(lower bound theorem)를 만족시킨다(Wang and Skirrow, 2008). 흙이나 암석의 항복함수로 자주 이용되는 Mohr-Coulomb(M-C)식이나 Heok-Brown(H-B)식(Hoek, 1983)을 적용할 경우 응력에 대한 1계 연립편미분방정식으로 표현되는 평형조건식은 쌍곡선형(hyperbolic) 미분방정식이다. 따라서 slip-line 해석법은 수학적으로 특성곡선(characteristic line)법을 이용하는 쌍곡선형 미분방정식 해법과 동일하다 (Hill, 1960, Hoffman, 2001, Davis & Selvadurai, 2002). 이 때 소성영역 내에 형성되는 잠재적 파괴면들이 특성곡선에 해당한다. 평형방정식을 특성곡선 좌표계로 전환하면 평형방정식은 해석적으로 적분이 가능한 간단한 형태가 되므로 특성곡선을 따라 변화하는 응력분포를 해석적으로 계산하는 것이 가능해진다.
Slip-line 해석법은 구조물 전체 영역 중 소성화된 일부 영역만을 해석대상으로 하므로 유한요소법이나 유한차분법과 같은 연속체 해석법에 비해 간편한 해석법이라는 장점이 있다. 그러나 강체소성(rigid plastic) 거동을 가정하므로 변형률경화나 변형률연화를 고려하기 힘들다는 단점이 있다. 또한 대상 구조물의 형상이 비교적 단순하여 소성영역의 형상을 미리 예측할 수 있는 연속체 매질에만 실용적으로 적용할 수 있다는 제약을 가진다. 이에 따라 slip-line 해석법은 지반공학 분야에서 얕은 기초나 제방의 지지력 계산, 등방 지압조건을 가정한 원형터널의 소성영역 깊이와 지보압 계산 등에 주로 활용되고 있다(Yu, 2006, Davis & Selvadurai, 2002, Wang & Skirrow, 2008). 최근에는 해저 파이프라인의 지지력 계산을 위해 이 해석법을 적용한 사례도 보고되고 있다(Gao et al., 2015).
암반공학 분야에서 slip-line 해석법을 활용한 연구사례는 지반공학 분야에 비해 상대적으로 적은 것으로 파악되고 있다. 이는 암반이 다수의 절리면을 포함하는 불연속체적 특성이 강한 매질이기 때문으로 판단된다. 절리가 잘 발달된 경암층의 경우 지압이 크지 않으면 파괴면의 형성은 절리면의 방향성 분포특성에 영향을 받기 쉬우므로 slip-line 해석법의 적용이 곤란하다. 하지만 절리면의 영향이 상대적으로 작아지는 고심도 지압조건의 암반, 연암, 무작위 방향성을 가지는 절리가 다수 분포하는 절리암반, 무결암 등의 경우는 암반을 연속체로 가정하여 안정성 해석을 수행하는 것이 가능하다(Hoek et al., 1995). 이에 따라 1990년대 이후 slip-line 해석법을 암반기초의 지지력계산에 적용하려는 연구들이 시도되고 있다(Serrano & Olalla, 1994, 2002, Serrano et al., 2016). Keshavarz et al.(2016)은 slip-line 해석법을 적용하여 지진하중을 고려한 암반기초의 지지력 계산을 시도하였다.
한편 국내에서는 slip-line 해석법과 유사한 해석적 접근법으로서 한계해석(limit analysis)의 상계해(upper bound solution)를 응용하여 암반의 등가점착력 및 등가마찰각을 추정하는 연구(Lee, 2015)가 수행된 사례는 있지만 아직까지 slip-line법을 암반구조물 해석에 적용한 사례는 보고되지 않고 있다. 이 연구에서는 인위적 혹은 자연적으로 이미 형성된 V자형 암석 노치에 쐐기가 삽입되어 노치가 파괴되는 상황을 가정한 후 V형 암석노치의 파괴하중을 slip-line법을 활용하여 계산하는 해석적 절차를 개발하고 그 성능을 평가함으로써 slip-line 해석법의 암반공학적 응용 가능성을 제시하였다.
2. Slip-line법을 이용한 응력분포 계산 원리
2.1 slip-line의 개념
2차원 응력조건을 가정할 때 한 점에서 응력상태는 다음과 같은 2차원 행렬식으로 표시할 수 있다.
| $$\boldsymbol\sigma=\begin{bmatrix}\sigma_x&\tau_{xy}\\\tau_{xy}&\sigma_y\end{bmatrix}$$ | (1) |
마찰각(friction angle, ∅)과 점착력(cohesion, c)으로 정의되는 M-C식을 암석의 항복기준식으로 채택할 경우 항복영역 내 임의 지점에서 응력상태는 다음 조건식을 만족하여야 한다.
| $$q=p\sin\phi+c\;\cos\phi$$ | (2) |
여기서
| $$p=\frac{\sigma_x+\sigma_y}2,\;q=\sqrt{\left(\frac{(\sigma_x-\sigma_y)}2\right)^2+\tau_{xy}^2}$$ | (3) |
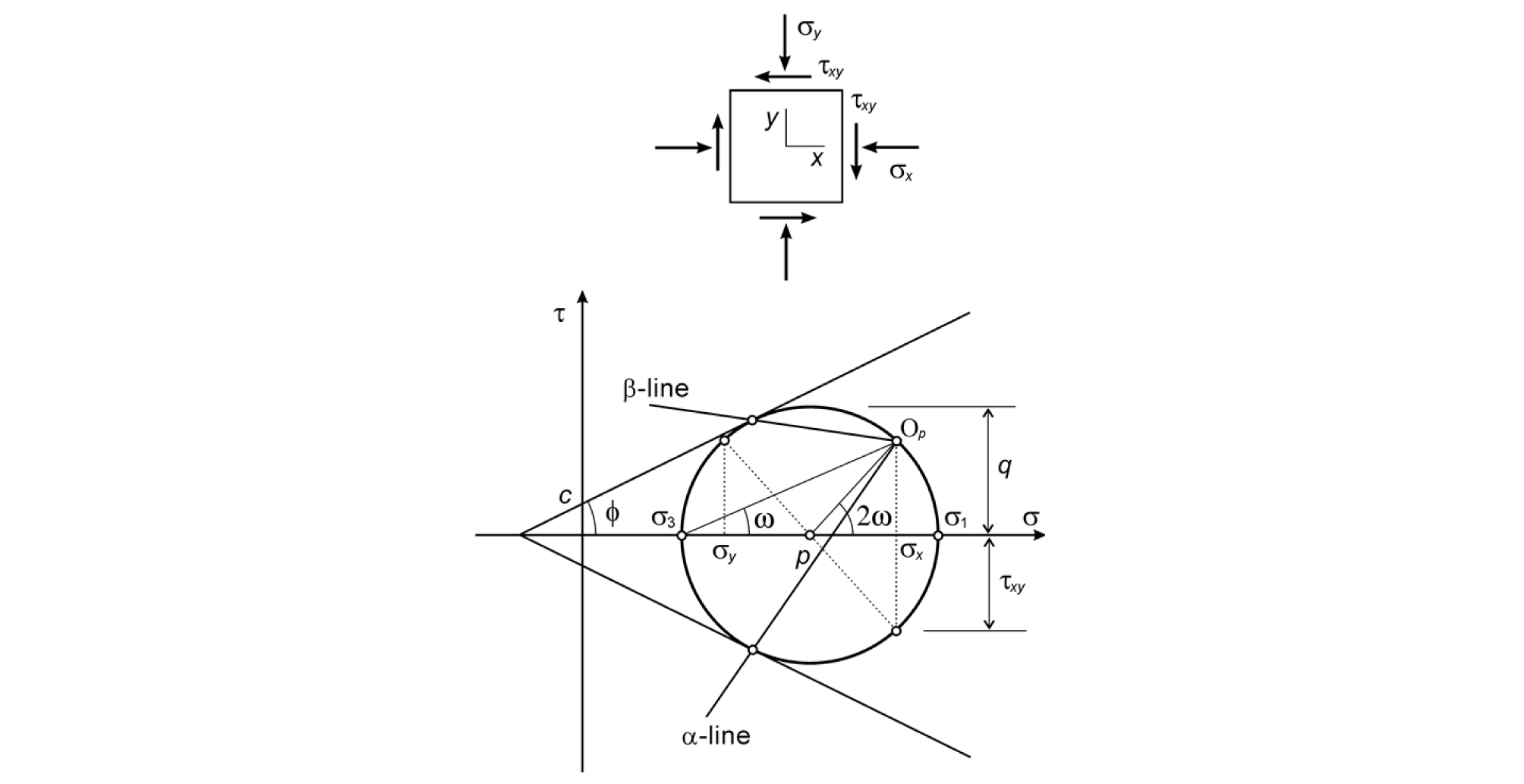
Fig. 1은 항복조건식 (2)를 만족하는 응력 σ의 Mohr 응력원을 보여준다. 여기에서는 편의를 위해 σx > σy을 가정하였고, x축 면에서 전단응력은 시계방향으로 작용하는 것으로 가정하였다. 점 Op는 응력 σ의 극점(pole)이며 평면기점(origin of plane)으로 불리기도 한다(Das, 1998). 극점 Op와 최소주응력 좌표점(σ3, 0)을 연결하는 직선은 최소주응력이 작용하는 면과 평행하다. 항복상태를 가정하였으므로 M-C 직선식은 Mohr원과 두 점에서 접한다. 이 때 극점 Op와 하부 접점을 연결하는 직선을 α선(α-line)이라 하고, 극점과 상부 접점을 연결하는 직선을 β선(β-line)이라 한다(Hill, 1960, Davis & Selvadurai, 2002). Slip-line이라 불리는 α선과 β선은 파괴면과 평행하고 두 선의 교차각은 (π/2 - ∅/2)이다. 소성영역에서 위치에 따라 응력 값이 연속적으로 변화하는 경우 α선과 β선의 연장은 곡선이 되지만 응력분포가 균질한 영역에서는 두 파괴선이 모두 직선으로 나타난다.
2.2 Slip-line 방정식
자중을 무시할 경우 식 (1)을 구성하는 3개의 응력성분 σx, σy, τxy이 정역학적 평형을 유지하기 위해서는 다음의 두 평형조건식을 만족하여야 한다.
| $$\frac{\partial\sigma_x}{\partial x}+\frac{\partial\tau_{xy}}{\partial y}=0$$ | (4a) |
| $$\frac{\partial\tau_{xy}}{\partial x}+\frac{\partial\sigma_y}{\partial y}=0$$ | (4b) |
그러므로 소성영역의 응력분포를 계산하는 문제는 식 (2)와 식 (4)를 동시에 만족하는 소성평형 상태의 응력성분을 구하는 문제로 귀착된다. 구해야할 응력성분의 수와 주어진 조건식의 수가 모두 세 개이므로 소성평형 상태의 응력성분을 구하는 것이 이론적으로 가능하다.
한편, 최소주응력면과 x축의 사이각을 ω라 하면 Fig.1에서
| $$\sigma_x=p+q\;\cos2\omega$$ | (5a) |
| $$\sigma_y=p-q\;\cos2\omega$$ | (5b) |
| $$\tau_{xy}=q\;\sin\;2\omega$$ | (5c) |
이다. 식 (2)에 의해 q는 p로 표현할 수 있으므로 식 (5)을 식 (4)에 대입하면 소성 평형방정식 (4)은 두 미지수 p와 ω에 대한 1계 연립 편미분방정식으로 다음과 같이 변형될 수 있다.
식 (6)으로 표시된 연립미분방정식은 쌍곡선형(hyperbolic) 편미분방정식이므로 해석영역 경계의 응력분포 정보가 특성곡선(characteristic path)을 따라 영역내로 전파된다(Hoffman, 2001). M-C 항복함수를 가정한 탄소성 응력해석의 경우 앞 절에서 설명한 α선과 β선이 특성곡선 역할을 하게 된다.
α선을 따라 측정한 곡선길이를 sα라 하면 p의 α선 방향의 방향미분은
| $$\frac{dp}{ds_\alpha}=\frac{\partial p}{\partial x}\frac{\partial x}{\partial s_\alpha}+\frac{\partial p}{\partial y}\frac{\partial y}{\partial s_\alpha}$$ | (7) |
이다. 식 (6)을 활용하여 식 (7)을 간단히 하면 α선의 특성을 정의하는 미분식을 다음과 같이 얻을 수 있다.
| $$\frac{\cos\phi}{2(p\sin\phi+c\cos\phi)}\frac{dp}{ds_\alpha}+\frac{d\omega}{ds_\alpha}=0\;\;\mathrm{또는}\;\frac{\cos\phi}{2(p\sin\phi+c\cos\phi)}dp+d\omega=0$$ | (8) |
β선의 특성을 나타나는 미분식도 유사한 과정을 거쳐 얻을 수 있으며 식 (8)의 + 부호를 –부호로 바꾸면 그 결과식이 된다.
식 (8)의 두 번째 식에서
| $$dI=\frac{\cos\phi}{2(p\sin\phi+c\cos\phi)}dp$$ | (9) |
라고 하면
| $$I(p)=\int\frac{\cos\;\phi}{2(p\sin\phi+c\cos\phi)}dp=\frac12cot\;\phi\;\ln\;(p\;\sin\;\phi+c\cos\phi)$$ | (10) |
이므로 α선에서는 다음의 불변량 관계식이 성립한다.
| $$I(p)+\omega=K$$ | (11) |
여기서 K는 적분상수이다. 그러므로 식 (11)은 α선이 통과하는 모든 위치에서 I(p)와 ω의 합은 변하지 않는다는 사실을 말해준다. 식 (11)의 I(p)는 Riemann 불변량이라고도 불린다(Serrano & Olalla, 1994). 불변량 관계식을 이용하면 소성영역의 한 지점 (1)에 작용하는 응력정보를 이용하여 다른 지점 (2)에 작용하는 응력의 크기를 구할 수 있다. 두 지점이 α선으로 연결되어 있고 지점 (2)을 포함하는 면에 작용하는 응력벡터(traction)의 방향을 미리 알고 있는 경우 지점 (2)에 작용하는 응력의 크기는 다음의 불변량 관계식을 이용하여 계산할 수 있다.
| $$I(p_{(1)})+\omega_{(1)}=I(p_{(2)})+\omega_{(2)}$$ | (12) |
여기서 p와 ω의 하첨자 (1)과 (2)는 해당 경계면 번호를 나타낸다.
3. V형 암석노치의 파괴하중 계산 원리
3.1 해석모델
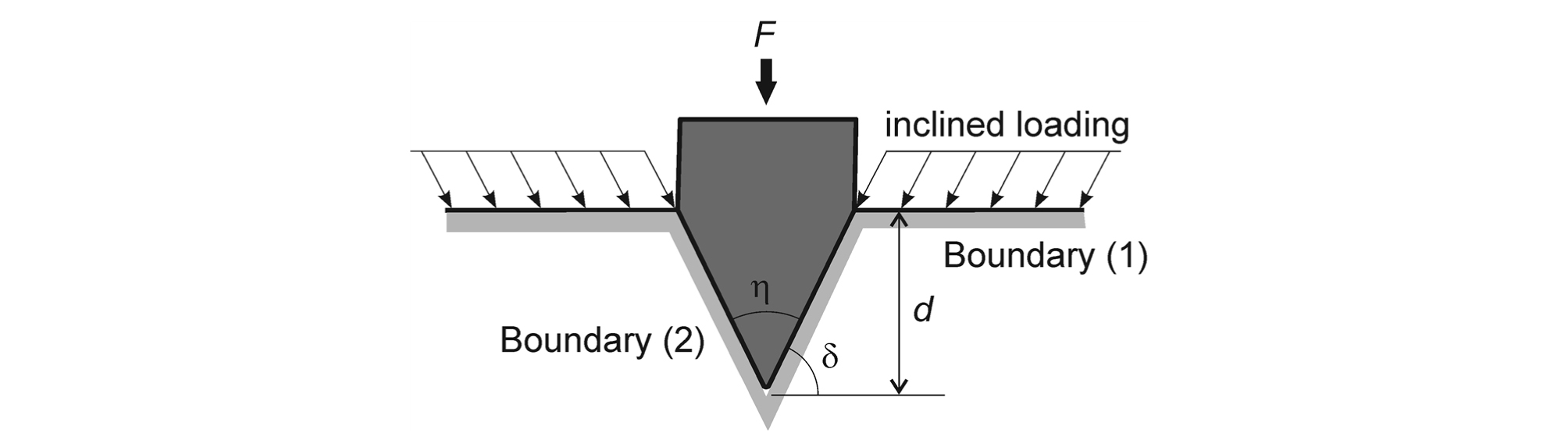
Fig. 2와 같이 각도 η, 깊이 d인 암석노치에 동일한 선단 각도를 갖는 쐐기가 삽입되어 암석이 파괴되는 상황을 가정하였다. 쐐기와 암석의 접촉면(경계(2)) 그리고 상부 수평면(경계(1))에 균질한 응력이 작용한다면 2절에서 설명한 slip-line 법을 적용하여 노치의 파괴하중을 계산하는 것이 가능하다. 해석모델의 일반화를 위해 상부 수평경계면에도 균질한 경사하중이 작용하는 상황을 가정하였다. 해석 모델의 대칭성을 고려하여 모델의 우측 부분만을 해석 대상으로 설정하였다.
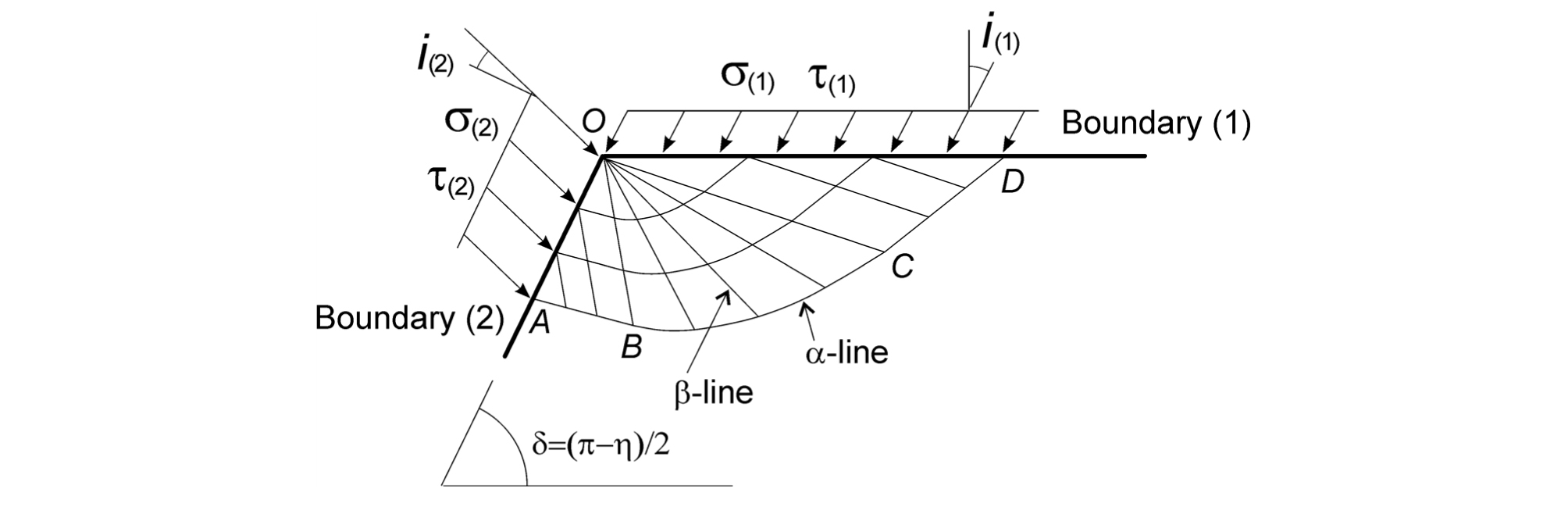
암석노치에 가해지는 하중이 증가하면 노치 주변의 암석은 소성파괴 상태에 도달하게 되고 소성영역에서는 Fig. 3과 같은 slip-line 망이 형성된다. 경계면(1)과 경계면(2)에 각각 균질한 응력 (σ(1), τ(1)), (σ(2), τ(2))이 작용하고 있으므로 두 경계에 접하는 영역 OCD와 영역 OAB에는 균질한 응력이 분포한다. 이에 따라 영역 OCD와 영역 OAB에서 α선과 β선이 모두 직선으로 나타난다. 이 때 영역 OAB는 주동영역(active zone)이며 되며 영역 OCD는 수동영역(passive zone)이 된다. 주동영역과 수동영역의 사이에 위치한 영역 OBC은 전이영역(transition zone) 역할을 하며 이 영역에서 α선은 대수나선(log-spiral) 곡선이 된다. 전이영역에서 β선들은 O에서 시작하여 반경방향으로 멀어지는 직선으로 나타난다. 전체적으로 α선들은 점 O를 감싸고 회전하면서 경계면(1)과 경계면(2)를 연결하는 형태로 나타난다. M-C 항복함수를 채택하였으므로 α선과 β선이 교차하는 모든 지점에서 교차각은 항상 (π/2 - ∅/2)이 된다.
3.2 불변량 관계식을 이용한 경계응력 결정
Fig. 3을 참조하면 경계면(1)과 경계면(2)에 작용하는 수직응력(σ)과 전단응력(τ)의 관계는 각각 다음과 같다.
| $$\tau_{(1)}=\sigma_{(1)}\;\tan\;i_{(1)}$$ | (13) |
| $$\tau_{(2)}=\sigma_{(2)}\;\tan\;i_{(2)}$$ | (14) |
여기서 i(1)와 i(2)는 각각 경계면(1)과 경계면(2)에 작용하는 하중의 경사각이며 모두 기지의 값으로 가정한다. σ(1)=0인 경우 i(1)은 정의되지 않으며 이 때 τ(1)≠0이면 이 전단응력 값이 직접 사용된다. 경계면(2)에서 응력은 주동(active) 상태이므로 쐐기와 암석노치 면의 마찰특성을 반영하는 경사각 i(2)는 다음의 제약조건을 만족해야한다.
| $$i_{(2)}<\tan^{-1}\left[\frac{q_{(2)}}{p_{(2)}}\right]$$ | (15) |
수식 전개의 편의를 위해 연직하향 방향을 기준으로 최소주응력면까지 반시계방향으로 측정한 각도 Ω를 도입하면 Ω=π/2+ω의 관계가 있으므로 식 (12)는 Ω를 이용하여 다음 식으로 다시 표현할 수 있다.
| $$I(p_{(1)})+\Omega_{(1)}=I(p_{(2)})+\Omega_{(2)}$$ | (16) |
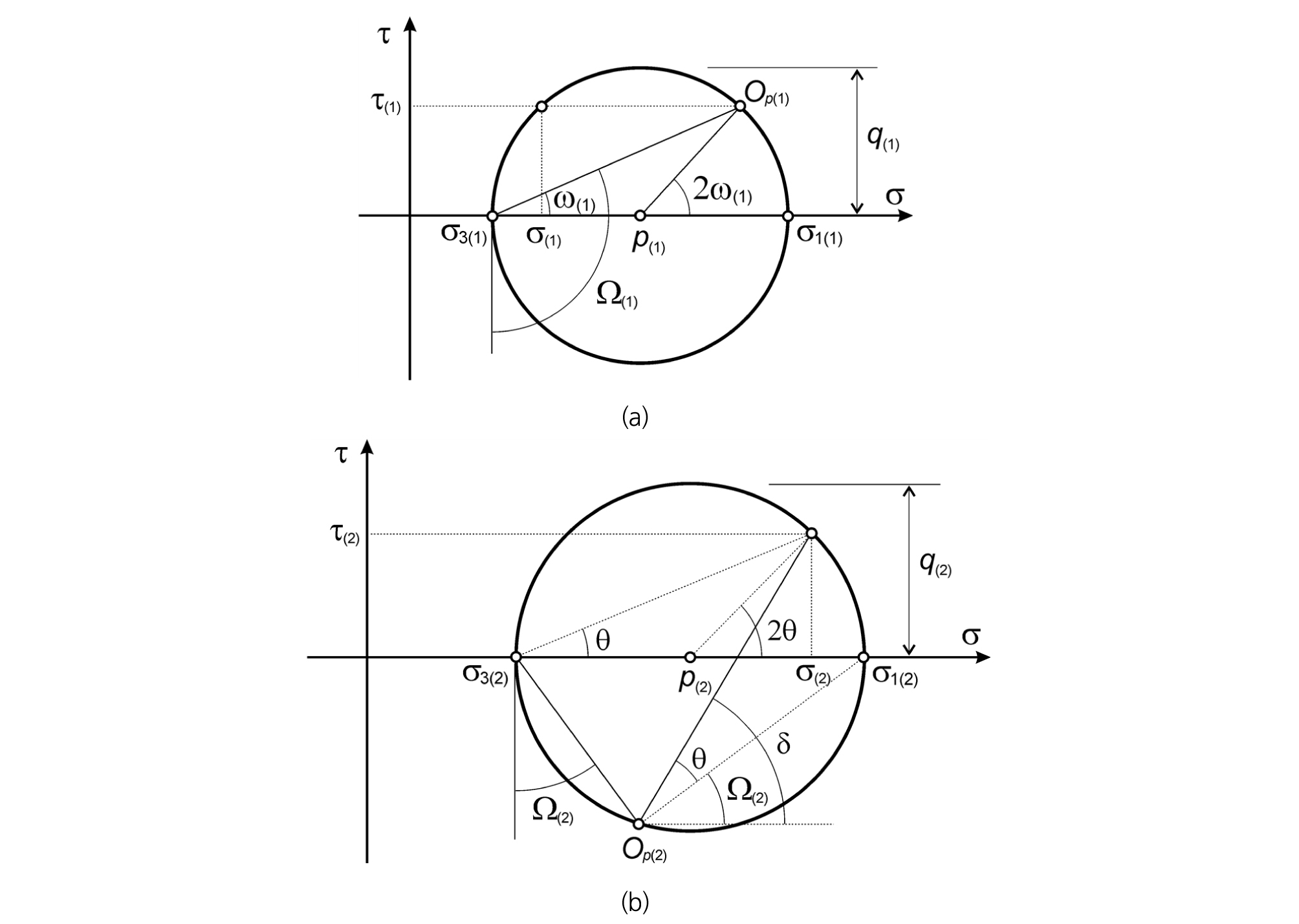
경계면(1)에 작용하는 응력의 Mohr원을 Fig. 4(a)에 도시하였다. Mohr원의 방정식은 다음 식으로 표시된다.
| $$\left[\sigma-p_{(1)}\right]^2+\tau^2=q_{(1)}^2$$ | (17) |
경계면(1)의 응력조건 (σ(1), τ(1))은 Mohr원 상의 한 점이므로 항복조건식 (2)과 식 (13)을 고려하면 식 (17)은 p(1)에 대한 2차 방정식이 되고 그 해는 다음 식과 같다.
| $$p_{(1)}=\frac{\sigma_{(1)}+c\cos\phi\;\sin\phi+\sqrt{\left[\sigma_{(1)}+c\cos\phi\sin\phi\right]^2-\cos^2\phi\left[\sec^2i_{(1)}\sigma_{(1)}^2-c^2\cos^2\phi\right]}}{\cos^2\phi}\;$$ | (18) |
만약 경계면(1)에서 σ(1) = 0, τ(1) ≠ 0이라면 p(1)은
| $$p_{(1)}=\frac{c\cos\phi\;\sin\phi+\sqrt{c^2\cos^2\phi\sin^2\phi-\cos^2\phi\left[\tau_{(1)}^2-c^2\;\cos^2\phi\right]}}{\cos^2\phi}\;$$ | (19) |
이다. 식 (18)식을 식 (10)에 대입하면 경계면(1)에서 I(p(1))은 다음과 같이 표현된다.
| $$I(p_{(1)})=\frac12\cot\;\phi\;\ln\;\left[p_{(1)}\;\sin\;\phi+c\;\cos\;\phi\right]$$ | (20) |
또한 Fig.4(a)를 참조하면 최소주응력면과 수평면이 이루는 각도 ω(1)는
| $$\omega_{(1)}=\frac12\sin^{-1}\left[\frac{\tau_{(1)}}{q_{(1)}}\right]$$ | (21) |
이므로 연직하향 방향을 기준으로 반시계방향으로 최소주응력면까지 측정한 각도 Ω(1)는 다음과 같이 계산될 수 있다.
| $$\Omega_{(1)}=\frac\pi2+\frac12\sin^{-1}\left[\frac{\sigma_{(1)}\tan\;i_{(1)}}{p_{(1)}\sin\phi+c\cos\phi}\right]$$ | (22) |
따라서 경계면(1)에서 불변량은 식 (20)과 식 (22)의 합이 된다.
한편, 경계면(2)에 작용하는 응력의 Mohr원은 Fig.4(b)에 도시한 것과 같고, 이 Mohr원의 방정식으로부터 다음 관계식이 성립한다.
| $$\lbrack\sigma_{(2)}-p_{(2)}\rbrack^2+\tau_{(2)}^2=q_{(2)}^2$$ | (23) |
식 (14)을 식 (23)에 대입한 후 σ(2)에 대해 풀면 다음의 결과를 얻을 수 있다.
| $$\sigma_{(2)}=\frac{p_{(2)}+\sqrt{p_{(2)}^2-\sec^2i_{(2)}\lbrack p_{(2)}^2-q_{(2)}^2\rbrack}}{\sec^2i_{(2)}}$$ | (24) |
또한, Fig. 4(b)에서
| $$\theta=\frac12\;\sin^{-1}\left[\frac{\tau_{(2)}}{q_{(2)}}\right]=\frac12\;\sin^{-1}\left[\frac{\sigma_{(2)}\tan\;i_{(2)}}{q_{(2)}}\right]$$ | (25) |
이므로 경계면(2)에서 연직하향 방향을 기준으로 최소주응력면까지 반시계방향으로 측정한 각도 Ω(2)는 다음 식과 같다.
| $$\Omega_{(2)}=\delta-\frac12\sin^{-1}\left[\frac{\sigma_{(2)}\;\tan\;i_{(2)}}{q_{(2)}}\right]$$ | (26) |
암석노치의 경사각 δ는 쐐기각도 η와 δ=(π-η)/2의 관계가 있으므로 식 (26)은 다시 다음과 같이 표시할 수 있다.
| $$\Omega_{(2)}=\frac\pi2-\frac\eta2-\frac12\sin^{-1}\left[\frac{\sigma_{(2)}\;\tan\;i_{(2)}}{q_{(2)}}\right]$$ | (27) |
이제,
| $$I(p_{(2)})=\frac12\cot\;\phi\ln\;\left[p_{(2)}\;\sin\phi+c\cos\;\phi\right]$$ | (28) |
이고
| $$q_{(2)}=p_{(2)}\;\sin\phi+c\;\cos\phi$$ | (29) |
이므로 식 (24), 식 (27), 식 (28), 식 (29)를 이용하면 경계면(2)의 불변량 I(p(2))+Ω(2)이 p(2)의 함수로 표시됨을 알 수 있다.
결과적으로 불변량 관계식 (16)에서 좌변은 기지의 값이고 우변은 p(2)에 대한 비선형 함수식이 되므로 적절한 수치해석적 방법을 이용하여 식 (16)의 해를 구하면 경계면(2)의 p(2) 값이 구해진다. 이 결과를 다시 식 (24)에 대입하면 노치 면에 작용하는 수직응력 σ(2)가 구해지며, 전단응력 τ(2)는 식 (14)에 의해 결정된다.
참고로 i(1) = i(2) = 0°이고 η = 180°이면 지금까지 설명한 경계응력 계산절차에 의해 계산한 σ(2) 값은 Prandtl 파괴 메카니즘을 기초로 유도된 줄기초(strip footing) 지지력 계산식(Davis & Selvadurai, 2002, Chen, 2008)인 다음 식 (30)을 이용한 계산결과와 정확히 일치함을 보일 수 있다.
| $$\sigma_{(2)}=\sigma_{(1)}N_q+cN_c$$ | (30) |
여기서
| $$N_q=e^{\pi\;\tan\;\phi}\;\tan^2\;\;\left(\frac\pi4+\frac\phi2\right),\;\;N_e=(N_q-1)\;\cot\;\phi$$ | (31) |
예를 들어 c = 5.0 MPa, ∅ = 40°, σ(1) = 0.1Mpa인 경우 두 방법에 의해 계산된 σ(2)의 값은 모두 382.99MPa이다.
4. 암석노치 각도와 경계면 마찰특성에 따른 노치 파괴하중 변화
4.1 노치의 파괴하중 계산식
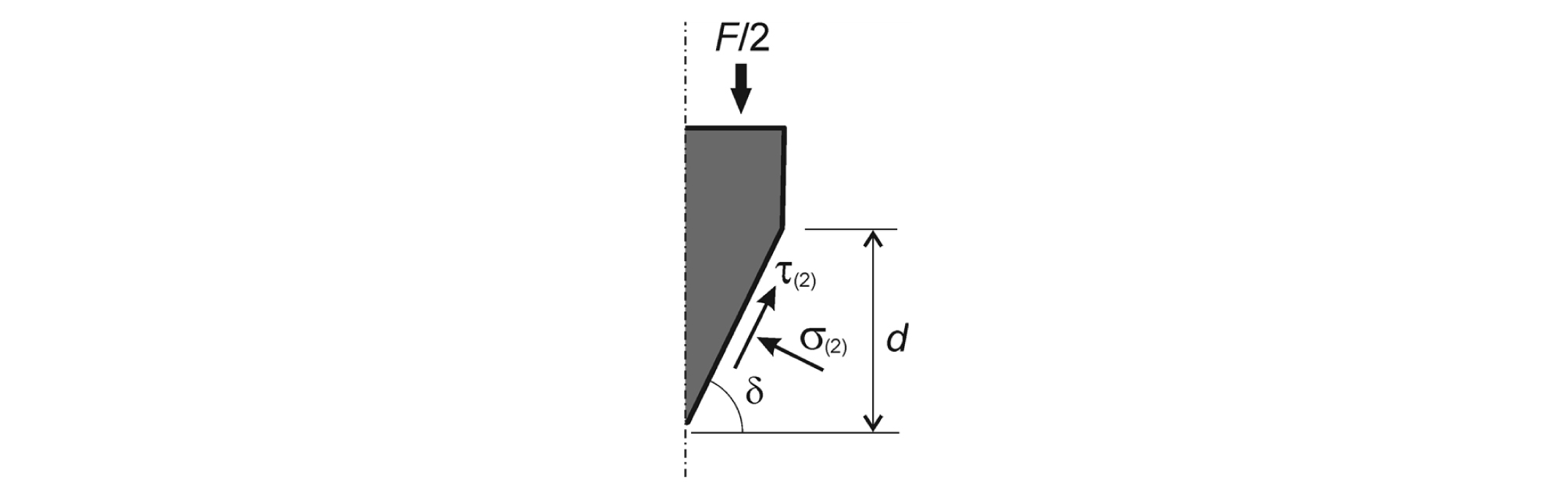
3절에서 설명한 방법에 의해 암석노치 경계면에 작용하는 응력 (σ(2), τ(2))이 계산되면 노치 파괴하중을 계산하는 것이 가능하다. Fig. 5를 참조하여 노치에 하중을 가하는 쐐기의 연직방향 힘의 평형을 고려하면 파괴하중 F에 대한 다음의 관계식이 얻어진다.
| $$\frac Fd=2\;\lbrack\tau_{(2)}+\sigma_{(2)}\;\cot\;\delta\rbrack$$ | (32) |
여기서 δ=(π-η/2)이고 τ(2) = σ(2)tani(2)의 관계가 성립하므로 식 (32)은 다시 다음 식으로 표현할 수 있다.
| $$\frac Fd=2\sigma_{(2)}\;\left[\tan\;i_{(2)}+\cot\left(\frac{\pi-\eta}2\right)\right]$$ | (33) |
쐐기의 두께를 단위 값으로 가정하면 식 (32)과 식 (33)의 좌변은 응력의 차원으로 간주할 수 있다.
4.2 노치 각도 변화와 파괴하중
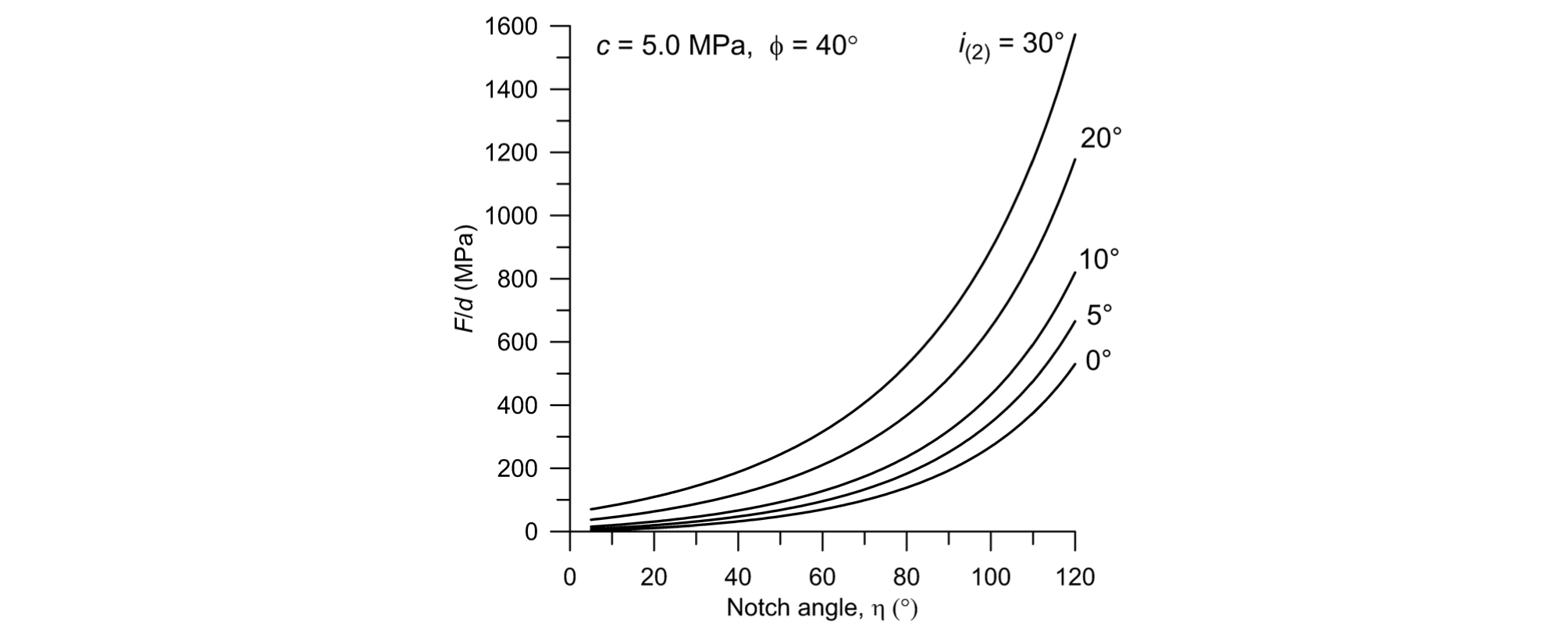
c=5.0 MPa, ∅ = 40°의 강도특성을 갖는 암석을 가정한 후 3절과 4.1절에서 설명한 원리에 따라 노치 각도 η의 변화에 따른 노치 파괴하중 F의 변화를 계산하였고, Fig. 6은 그 결과를 보여준다. 그래프에서 세로축은 파괴하중 F를 노치의 깊이 d로 나눈 값을 나타내며, 세로축의 수치는 노치 단면에 수직한 방향의 길이를 1m로 하는 2차 응력조건에서 계산한 결과이다. 그러므로 만약 F/d = 400 MPa이라면 이는 F/d ≃ 4 ton/cm를 의미한다. 파괴하중 계산과정에서는 σ(1) = τ(1) = 0을 가정하였다. 쐐기와 노치 면의 마찰특성을 반영하는 각도 i(2)는 5가지 경우 즉, 0°, 5°, 10°, 20°, 30°을 고려하였다. i(2) 값이 클수록 쐐기와 노치의 접촉면에서 접촉면과 평형한 방향의 마찰저항성이 커짐을 의미한다. i(2) = 0°는 노치 면에 전단응력이 작용하지 않고 수직응력만 작용하는 경우를 의미한다.
노치 각도가 증가함에 따라 파괴하중은 지수함수적으로 증가하는 특징이 있음을 Fig. 6은 잘 보여준다. 그러나 범위 η < 40°에서는 파괴하중 변화의 비선형성이 상대적으로 크지 않음을 알 수 있다. 또한 Fig. 6은 i(2)의 증가 즉 쐐기와 노치 면의 마찰이 증가하면 파괴하중이 크게 증가한다는 사실을 명확히 보여준다. 예를 들어 η = 40°일 때, i(2) = 0°이면 F/d ≃ 31.50MPa이지만 i(2) = 30°이면 F/d ≃ 187.89MPa으로 계산되므로 파괴하중이 약 6배 증가하는 것으로 나타났다. 반면에 η = 90°인 경우 i(2) = 0°일 때 F/d ≃ 192.85MPa이고, i(2) = 30°일 때 F/d ≃ 683.10MPa이므로 이 경우 파괴하중은 약 3.5배 증가하였다. 그러므로 마찰이 없는 매끄러운 노치 면(i(2) = 0°)을 가정한 파괴하중 계산 값과 비교할 때 노치 면과 쐐기면의 마찰을 고려한 파괴하중 계산 값은 노치 각도가 클수록 그 비율이 낮아짐을 알 수 있다.
4.3 노치 면의 마찰 특성 변화와 파괴하중
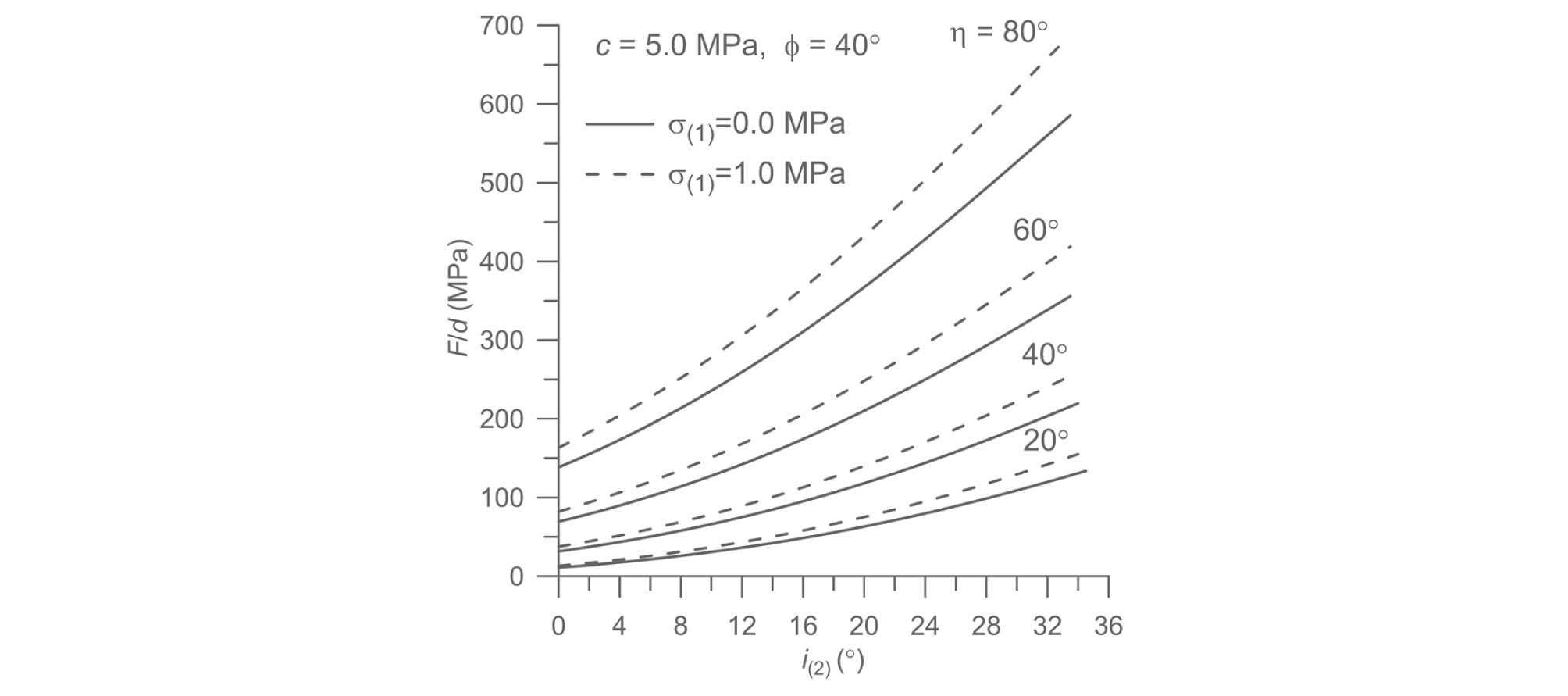
노치 면과 쐐기의 접촉면 마찰특성이 파괴강도에 미치는 영향을 살펴보기 위해 i(2)의 연속적 변화에 따른 노치 파괴하중의 변화를 계산하였다. 암석의 점착력과 마찰각은 4.2절의 경우와 동일하게 가정하였다. 여기에서는 노치 외부 수평면에 작용하는 수직응력 σ(1)이 각각 0.0MPa, 1.0MPa인 2가지 경우를 고려하였다. 또한 경계면(1)에서 τ(1) = 0.0, i(1) = 0.0을 가정하였다.
η = 20°, 40°, 60°, 80°인 4가지 경우에 대해 i(2) 변화에 따른 노치 파괴하중의 변화를 계산한 결과를 Fig. 7에 도시하였다. 가정한 암석에서 노치 면에 작용하는 응력이 주동상태를 유지할 수 있는 i(2)의 최대값은 η=10°일 때 약 35°이고 η=90°일 때 약 33°로 계산되었다. i(2)의 증가에 따라 노치 파괴강도는 비선형적으로 증가하는 경향을 보여주지만 비선형성은 크지 않는 것으로 나타났다. 또한 노치 각도가 클수록 i(2)의 증가에 대한 노치 파괴하중의 증가율은 더 크게 나타나고 있음을 보여준다. Fig.7은 또한 σ(1)이 0.0MPa에서 1.0MPa로 증가함에 따라 노치의 파괴하중이 상당히 증가함을 잘 보여준다. 예를 들어 σ(1)=0, i(2) = 30°일 때 F/d ≃ 187.89MPa이지만 σ(1)=1.0Mpa, i(2) = 30°이면 파괴하중은 F/d ≃ 222.07MPa으로 증가하였다. 이러한 계산결과는 노치 외부 수평면의 응력경계조건을 정확하게 설정하는 것이 암석노치의 파괴하중을 정밀하게 계산하는데 매우 중요하다는 사실을 말해준다.
5. 결 론
이 연구에서는 V형 암석노치에 쐐기가 삽입되어 하중을 가하는 상황을 가정한 후 소성해석법의 하나인 slip-line법을 기반으로 암석노치의 파괴하중을 계산하는 간단한 해석적 절차를 개발하였다. 개발된 방법에서는 2차원 응력조건을 가정하였으며 암석의 항복조건으로 M-C 함수가 채택되었다. 개발된 방법은 암석노치 면과 노치 외부 수평면에 균질한 경사하중이 작용하는 경우를 고려할 수 있으므로 보다 다양한 응력 경계조건에서 노치의 파괴하중을 계산하는 것이 가능하다.
암석 노치 면에 가해지는 하중에 의해 노치 면 주변에 형성된 소성영역이 외부 수평면까지 확장되면 암석 노치의 파괴가 발생한 것으로 간주하였다. 소성영역에 형성되는 slip-line 중에서 α선은 암석노치 면과 외부 수평면을 연결시키며 α선을 따라서 크기가 변하지 않는 불변량이 존재한다는 이론적 사실이 이 연구의 핵심 아이디어로 활용되었다. 노치 면 외부 수평면에 작용하는 기지의 응력조건을 이용하여 불변량 값이 계산되면 이 값의 불변성을 이용하여 암석 노치 면에 작용하는 수직응력과 전단응력을 계산하였다.
개발된 방법의 활용성을 검토하기 위하여 암석노치의 각도 변화, 암석노치와 쐐기면의 마찰특성 변화에 따르는 파괴하중 변화를 계산하였다. 노치 각도의 증가에 따라 파괴하중은 지수함수적으로 증가하는 것으로 나타났다. 노치 면과 쐐기면 경계의 마찰계수 증가에 따라 노치 파괴강도 증가는 역시 비선형적 경향을 보여주지만 비선형성은 상대적으로 크지 않는 것으로 나타났다.
유한요소법이나 유한차분법과 같은 범용 수치해석법과 달리 slip-line 해석법에서는 해석대상 구조물 전체 영역을 요소로 분할하지 않고 단지 소성영역 내에서 slip-line을 따라 소성 평형상태의 응력분포를 해석적 방법으로 계산한다. 그러므로 해석대상 구조물의 기하학적 형상과 응력 경계조건이 비교적 단순한 경우 기존의 범용 수치해석법보다 간편하고 신속하게 구조물의 파괴하중을 계산할 수 있다는 장점이 있다. 따라서 이 연구를 통해 개발된 방법론은 V형 노치 형성을 통한 암석 균열 유도 연구나 TBM 커터에 의한 암석파쇄 메커니즘을 이해하기 위한 간단한 해석적 도구로 활용될 수 있으며 나아가 원형터널, 암반사면, 암반 직접기초, V자형 선단형상으로 암반에 근입되는 말뚝기초의 해석 등에 유용하게 응용될 수 있을 것으로 기대된다.