1. 서 론
2. Modified Cam Clay (MCC) model
2.1 MCC 모델에서의 비체적(specific volume, ν)
2.2 MCC 모델에서의 경화법칙(Hardening rule)
3. Barcelona Basic Model (BBM)
3.1 BBM에서의 비체적(specific volume, υ)
3.2 BBM에서의 항복면(yield surface)
4. 결 언
1. 서 론
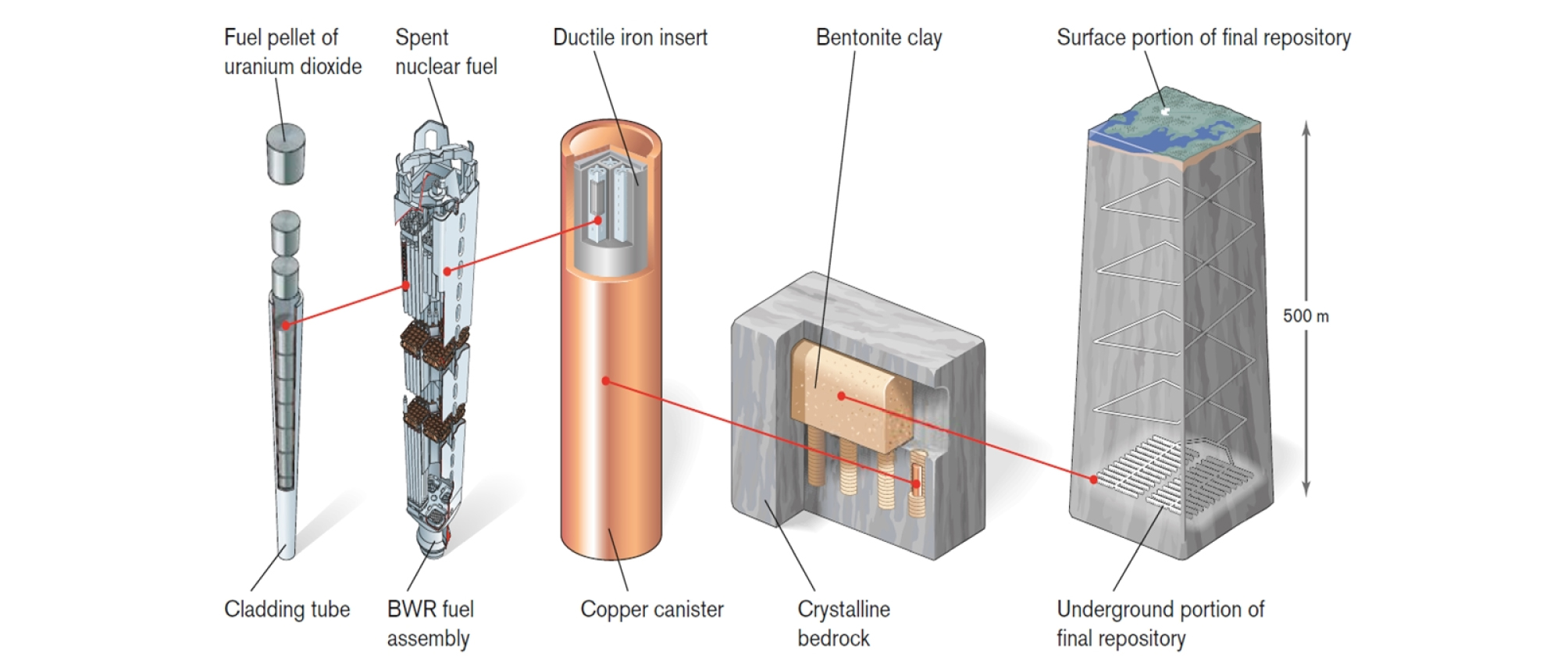
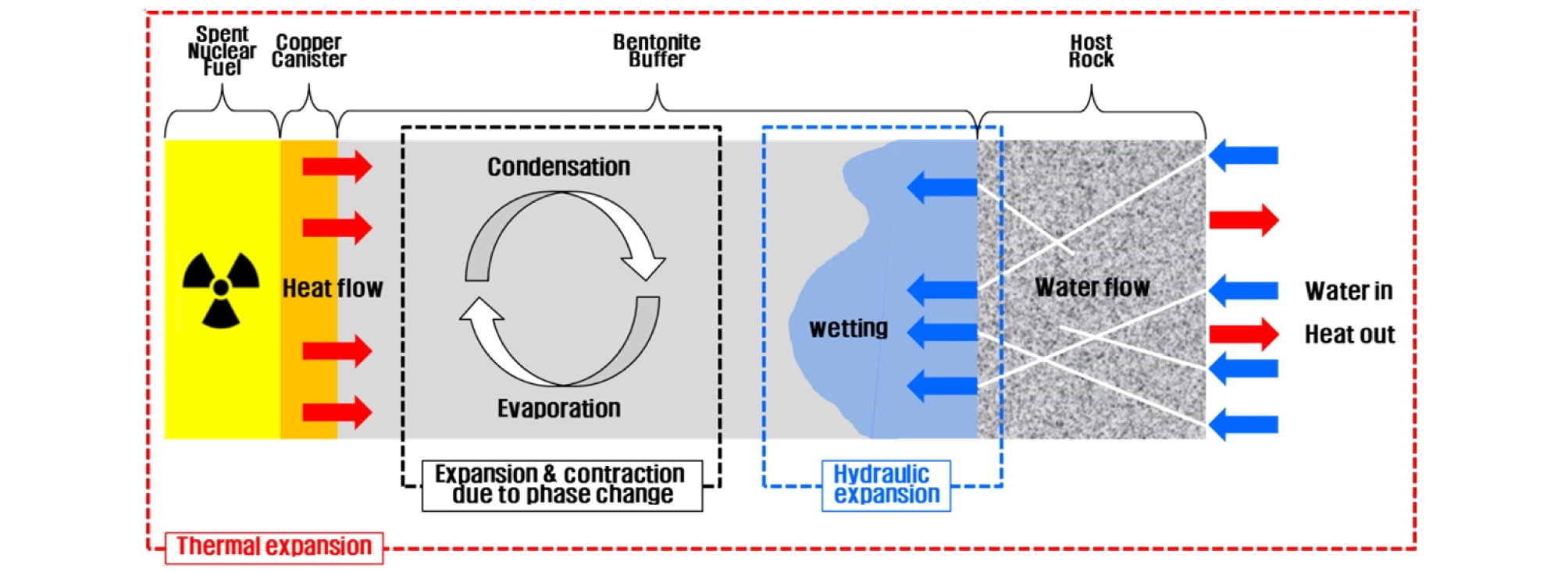
고준위방사성폐기물을 안전하게 처분하기 위해 제안된 심층처분방식은 공학적방벽(Engineered Barrier System, EBS)과 자연방벽(Natural Barrier System, NBS)으로 구성된 다중방벽시스템(multi-barrier system)을 이용하는 것으로써, Fig. 1과 같이 지하 수백 미터 깊이의 암반에 처분터널을 굴착하고 처분용기를 공학적방벽 물질인 벤토나이트 완충재와 함께 처분공에 처분한 후, 뒷채움재(backfill materials)로 처분터널을 완전히 메워 안전하게 격리하는 방식이다. 이러한 처분시스템에서는 Fig. 2와 같이 고준위방사성폐기물의 고유한 특성인 붕괴열에 의한 열적 거동 변화와 주변 암반으로부터의 지하수 유입에 따른 수리적 거동 변화가 예상되며, 열-수리 복합거동 변화에 따른 열-수리-역학적 복합거동(coupled thermo-hydro-mechanical behavior) 변화 역시 예상된다. 이러한 열-수리-역학적 복합거동은 처분시스템의 안정성에 영향을 미칠 수 있기 때문에 열-수리-역학적 복합거동 특성에 대한 이해와 이를 예측 및 평가할 수 있는 모델은 반드시 필요하다.
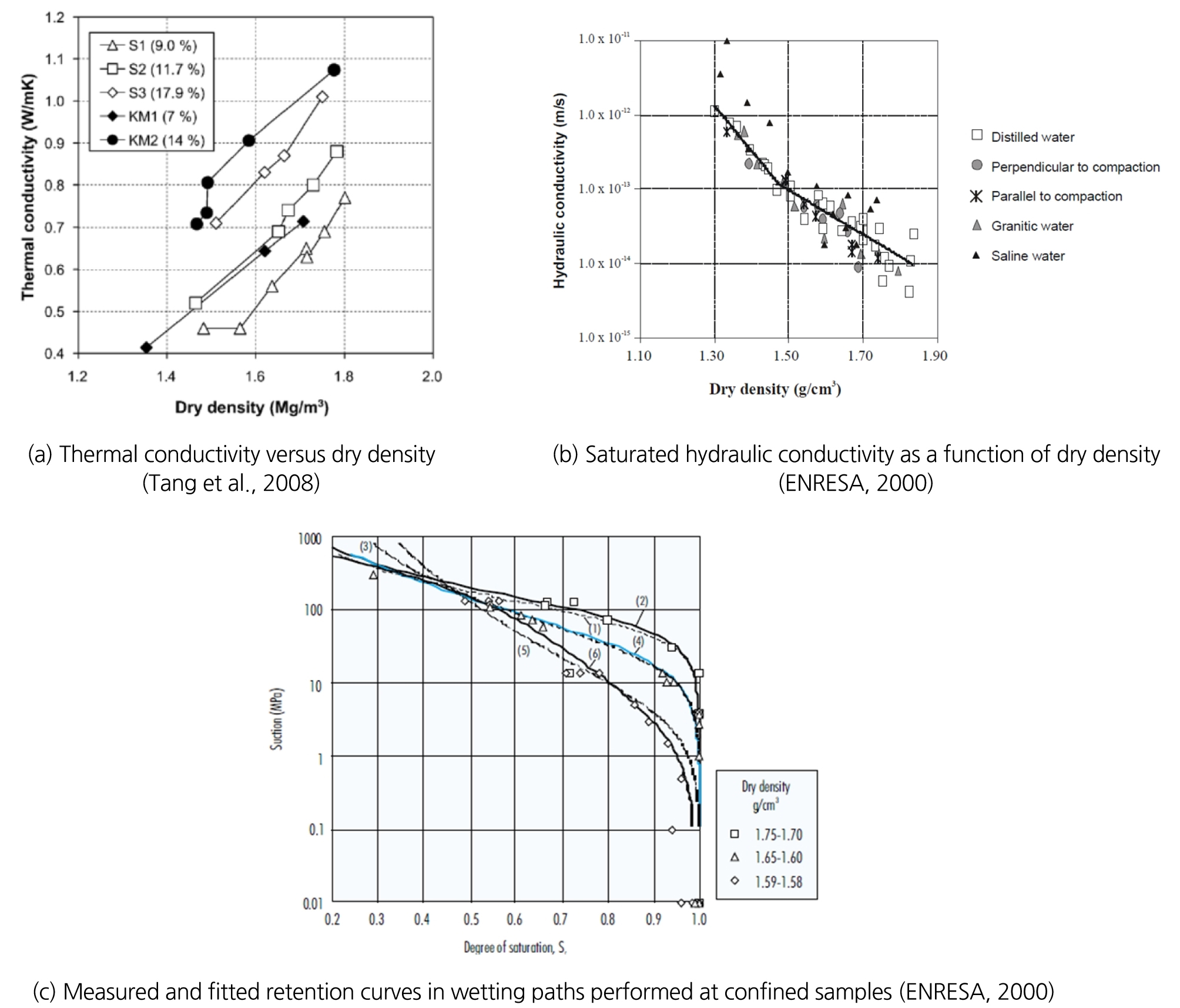
특히, 공학적방벽재인 벤토나이트 완충재에서는 온도 증가로 인해 공극에 포함되어 있는 물의 상(phase)이 변화하게 되고, 주변 암반으로부터의 지하수 유입으로 인해 벤토나이트 완충재의 포화도(saturation)가 변화하게 된다. 그 뿐만 아니라, 포화도 변화에 따른 완충재의 흡입력(suction) 변화는 팽윤압 변화를 초래하여 처분시스템 전반의 역학적 거동을 변화시킬 수 있으므로, 온도 변화와 흡입력의 변화에 따른 벤토나이트 완충재의 역학적 거동 특성을 모사할 수 있는 모델이 반드시 필요하다. 또한, 벤토나이트 완충재의 주요 특성인 열전도도, 투수계수, 그리고 흡입력은 Fig. 3에 나타나 있는 것처럼, 건조밀도(dry density, ρd)에 크게 영향을 받기 때문에 건조밀도 변화에 따른 열-수리적 복합거동 변화를 예측할 수 있는 모델이 반드시 필요하다.
Alonso et al.(1990)은 탄소성 모델인 Modified Cam Clay(MCC) 모델을 확장하여 불포화 지반에서의 역학 거동을 해석하기 위해 Barcelona Basic Model(BBM)을 제안하였다. Gens(1995)는 온도 변화에 따라 항복면(yield surface)이 변화되는 특성을 반영하여 BBM을 열・탄소성 모델(thermo-elasto-plastic model)로 수정하여 제안하였다. 이후, 수많은 BBM들이 제안되었으나 전반적으로는 BBM을 일부 변형한 것이라고 볼 수 있다(Sheng, 2011). 열・탄소성 해석 모델인 BBM은 연속체 해석 코드인 CODE_BRIGHT의 해석 모델로 개발되어(Olivella et al., 1996; CIEMAT, 2002), 불포화 지반과 공학적방벽의 완충재 물질로 고려되는 벤토나이트 및 벤토나이트-모래 혼합물에 대한 열-수리-역학적 복합거동 해석에 활용될 뿐만 아니라 처분시스템에서의 단기 및 장기 복합거동의 특성을 예측하고 이해하는데 널리 사용되고 있다(Li et al., 2013; Åkesson et al., 2010; Gaus et al., 2014; Gens at al., 2009). 이후, TOUGH-FLAC을 이용한 BBM을 이용한 해석 모듈이 개발되어 고준위방사성폐기물 처분장에서 예상되는 THM 복합거동 특성 평가에 활용되고 있을 뿐만 아니라(Rutqvist et al., 2011), 고준위방사성폐기물 처분 개념에 대한 성능평가에 활용되고 있다(Rutqvist et al., 2014).
본 논문에서는 국내 암반공학분야에서는 널리 알려져 있지는 않지만, 온도와 흡입력의 변화에 따른 역학적 거동 변화를 고려할 수 있기 때문에 공학적방벽재인 벤토나이트 완충재의 열-수리-역학적 복합거동을 잘 모사하는 것으로 알려진 BBM을 소개하고자 한다. 앞에서 언급하였듯이, BBM은 MCC 모델을 확장하여 만든 모델이기 때문에, 본 고에서는 MCC 모델을 먼저 간략하게 소개하고 난 이후, BBM에 대해 상세하게 기술하고자 한다.
2. Modified Cam Clay (MCC) model
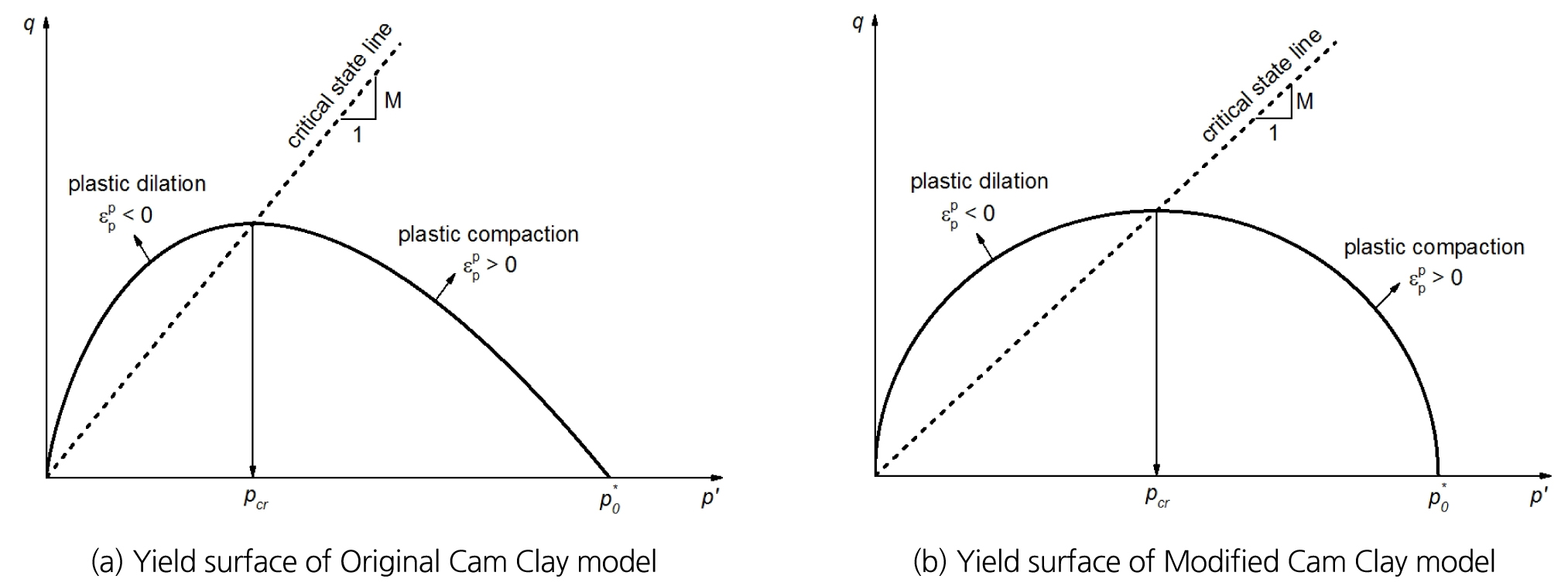
Cam Clay 모델은 영국 Cambridge 대학에서 한계상태(critical state) 이론을 바탕으로 제안된 탄소성(elasto-plastic) 모델로서, Roscoe and Scofield(1963)에 의해 제안되었다. 이후, 변형률을 과대평가하고 팽창비가 유한한 값을 갖는 모순점을 극복하기 위해 Roscoe and Burland(1968)에 의해 MCC 모델이 제안 되었다. 기본적으로 Original Cam Clay 모델과 MCC 모델은 유사하지만 항복면을 정의하는 공식이 각각 식 (1)과 식 (2)로 다르게 표현되는 특징이 있다. 각각의 항복 곡선을 유효응력(pʹ)과 편차응력(q)의 평면에 도시하여 나타내면, Fig. 4에 나타나 있는 것처럼 Original Cam Clay 모델에서의 항복 곡선은 대수 나선(log spiral) 형태이지만, MCC 모델은 타원의 형상을 가진다.
| $$\frac q{p'}-Mn\left(\frac{p_0^\ast}{p'}\right)=0$$ | (1) |
| $$p'\left[\frac{(q/p')^2+M^2}{M^2}\right]-p_0^\ast=0$$ | (2) |
여기서, p0*는 선행압밀응력(preconsolidation pressure)이고, M은 물질상수이다.
2.1 MCC 모델에서의 비체적(specific volume, ν)
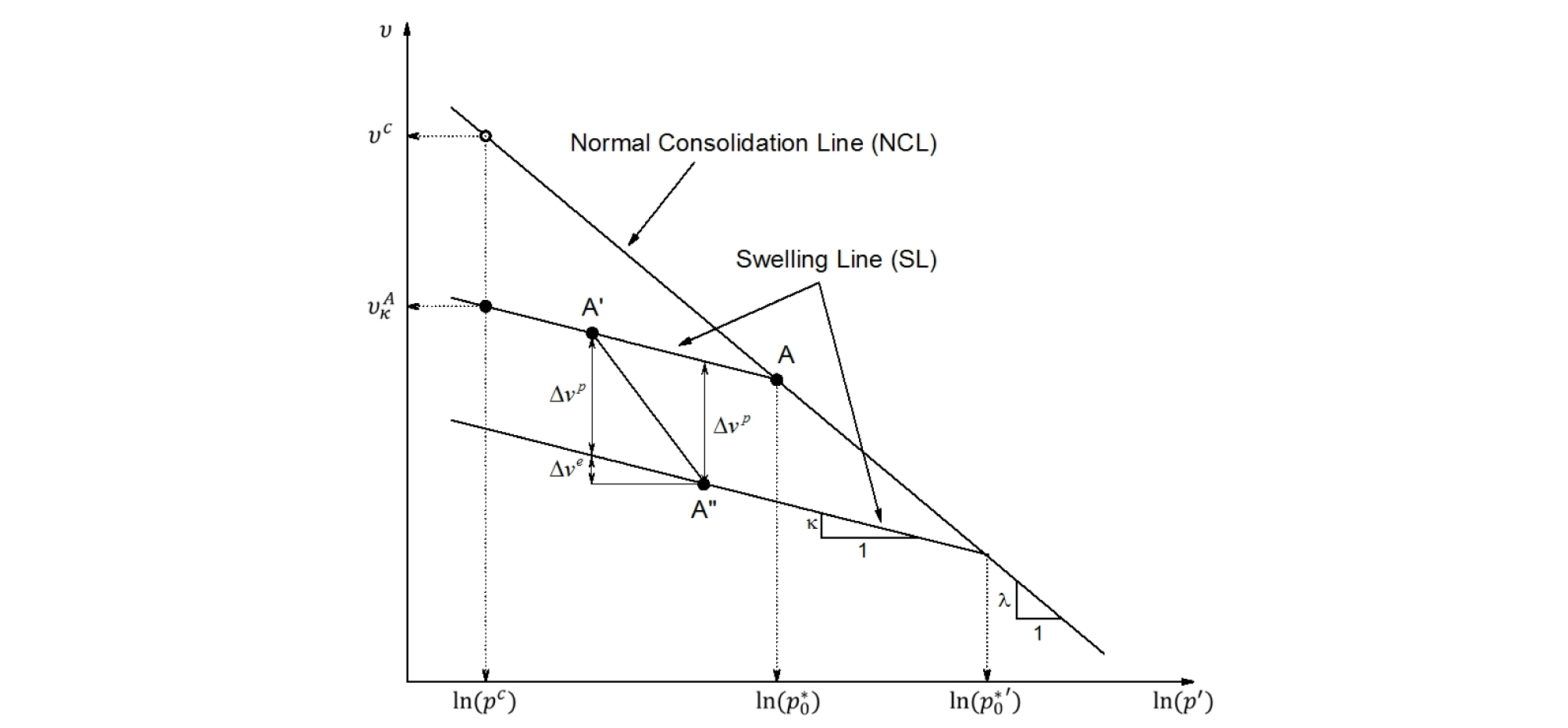
MCC 모델에서 정규압밀점토의 등방압축(isotropic compression)하에서의 식 (3)으로 정의되는 비체적의 변화는 Fig. 5에서 나타나 있는 것처럼 υ-ln(pʹ) 평면에서 기울기가 λ인 정규압밀선(Normal Consolidation Line, NCL)으로 표현되고, 정규압밀상태에서 하중이 제거되면 비체적은 기울기가 κ인 팽창선(swelling line, SL)을 따라 이동하게 된다. 만일, 기준응력(reference stress, pc)에서 응력이 A지점으로 이동하게 되면, 소성변형이 일어나게 되어 비체적의 변화는 식 (4)와 같이 계산되며, 하중이 제거되어 응력이 A지점에서 다시 pc로 이동하게 되면 탄성변형이 일어나게 되고, 비체적(υκA)은 식 (5)와 같이 계산된다.
| $$\upsilon=1+e=1+\frac{V_V}{V_S}$$ | (3) |
| $$\upsilon=\upsilon^c-\lambda ln\frac{\mathit p^{\mathit A}}{\mathit p^{\mathit c}}$$ | (4) |
| $$\upsilon_{\mathit\kappa}^{\mathit A}\mathit=\upsilon^{\mathit c}\mathit-\mathit(\lambda\mathit-\kappa\mathit)\mathit\;ln\frac{\mathit p^{\mathit A}}{\mathit p^{\mathit c}}$$ | (5) |
여기서, e는 간극비이며, VV와 VS는 각각 공극의 부피와 흙입자의 체적이다. 그리고 υc는 기준응력(pc)에서의 비체적을 의미한다.
2.2 MCC 모델에서의 경화법칙(Hardening rule)
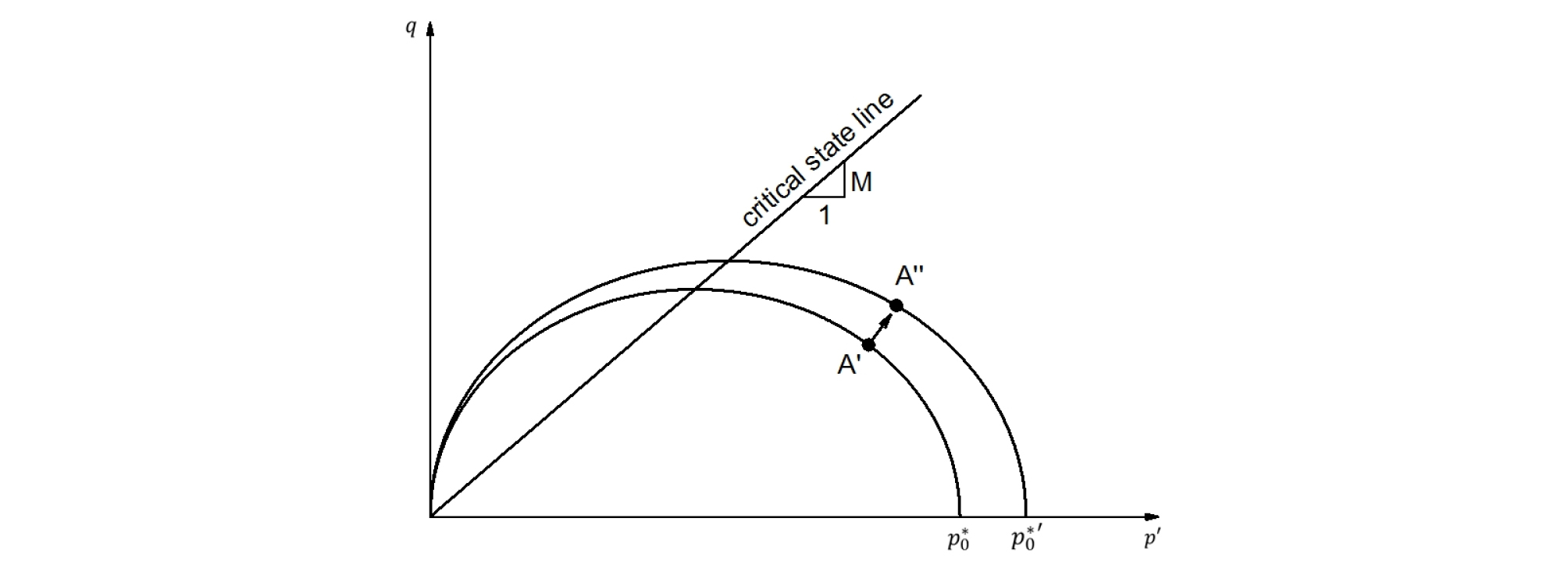
Fig. 6에 나타난 것과 같이 항복면에 위치한 Aʹ가 응력의 변화로 인해 Aʹʹ로 이동하면 소성변형이 발생하게 된다. 이때, 비체적 변화(∆υ)는 식 (6)과 같고, Fig. 5에 나타나 있는 탄성영역에서의 비체적 변화(∆υe)와 소성변형에 의한 비체적 변화(∆υp)는 각각 식 (7)과 식 (8)로 표현되며 소성체적변형률(εvp)은 식 (9)로 표현된다. 그리고 식 (9)를 p0*로 미분하면, 소성체적변화량(dεvp)는 식 (10)로 표현되며, 소성변형에 따른 경화 파라미터의 변화(dp0*)는 식 (11)에 의해 계산된다.
| $$\Delta\upsilon\mathit=\Delta\upsilon^{\mathit e}\mathit+\Delta\upsilon^{\mathit p}$$ | (6) |
| $$\bigtriangleup\upsilon^e=\kappa\ln\;(\frac{p^{A'}}{p^A})$$ | (7) |
| $$\bigtriangleup\upsilon^p=(\lambda-\kappa)\ln\;(\frac{p_0^{\ast'}}{p_0^\ast})$$ | (8) |
| $$\varepsilon_\upsilon^p=\frac{\bigtriangleup\upsilon^p}\upsilon=\frac{(\lambda-\kappa)}\upsilon\ln\;(\frac{p_0^{\ast'}}{p_0^\ast})$$ | (9) |
| $$d\varepsilon_v^p=\frac{(\lambda-\kappa)}\upsilon\;\frac{dp_0^\ast}{p_0^\ast}$$ | (10) |
| $$dp_0^\ast=p_0^\ast(\frac\upsilon{(\lambda-\kappa)})d\varepsilon_v^p$$ | (11) |
3. Barcelona Basic Model (BBM)
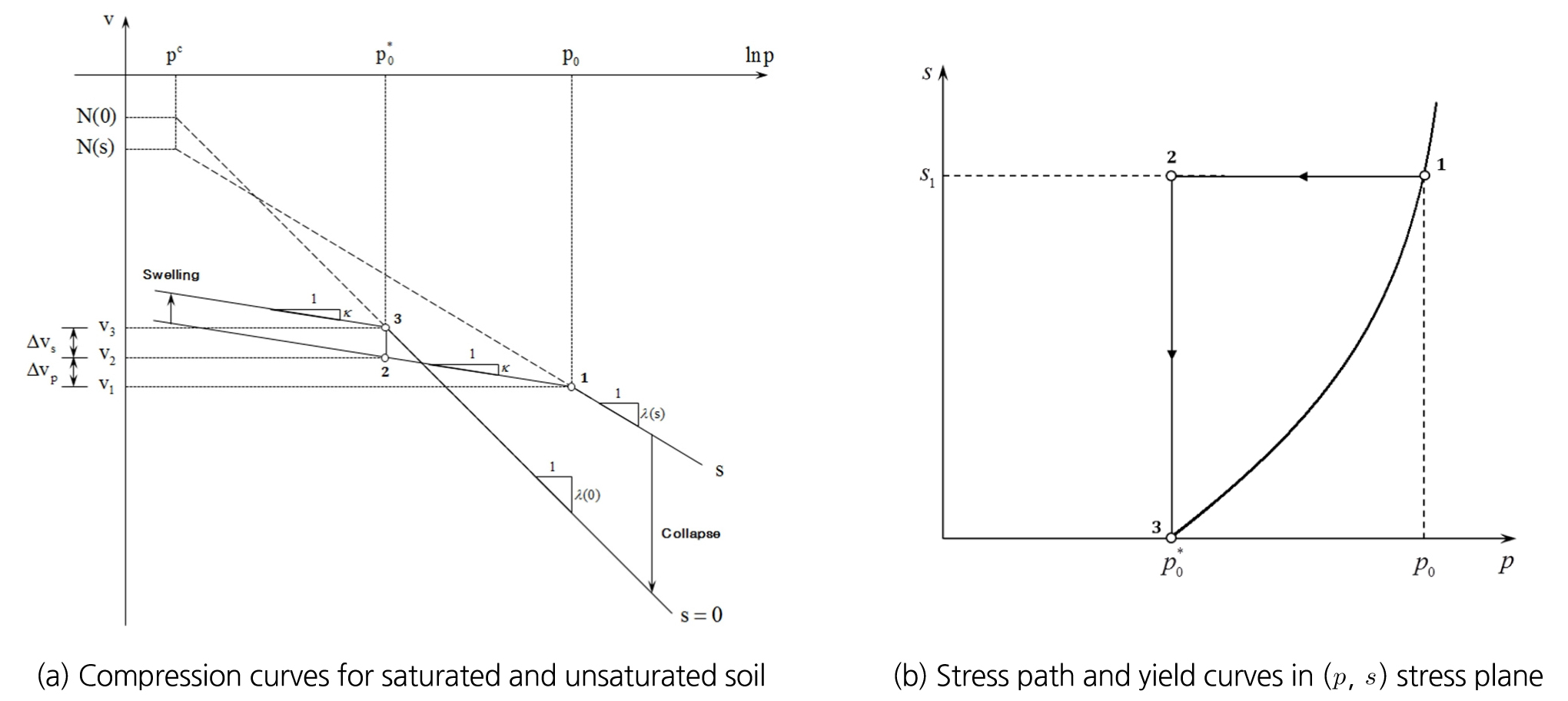
BBM은 MCC 모델을 확장한 모델로 Alonso et al.(1990)에서 처음 제안된 불포화 지반에 대한 탄소성 모델(elasto-plastic model)이다. Fig. 7(a)는 BBM에서의 유효응력(effective stress, p)과 흡입력(suction, s)의 변화에 따른 비체적(specific volume, v)의 변화를 나타낸 것으로서, BBM은 포화 상태(s=0)에서는 MCC 모델에서와 동일하지만, 불포화 상태(s≠0)에서는 정규 압밀 압축지수(compressibility parameter in virgin soil states, λ(0)가 흡입력에 대한 함수의 형태(λ(s))로 표현되는 특징이 있다. 또한 BBM은 불포화 지반의 포화도(saturation)가 변화하여 흡입력이 Fig. 7(b)에 나타나 있는 것처럼, 2지점에서 3지점으로 이동하여 발생하는 팽윤(swelling) 거동을 모사할 수 있는 역학적 모델이다.
3.1 BBM에서의 비체적(specific volume, υ)
흡입력(s)와 유효응력(p)에서의 비체적(υ)과 정규압밀 압축지수(λ(s))는 각각 식 (12)와 식 (13)과 같이 표현된다(Fig. 7(a)).
| $$\upsilon=N(s)-\lambda(s)\ln(\frac p{p^c})$$ | (12) |
| $$\lambda\;(s)=\lambda(0)\lbrack(1-r)\;exp\;(-\beta\cdot s)+r\rbrack$$ | (13) |
여기서, pc는 기준 응력(reference stress state for v-p relation in virgin states)을 의미하며, N(s)는 불포화 상태일 때 기준 응력에서의 비체적을 의미하고, λ(s)와 λ(0)는 각각 불포화 및 포화상태에서의 정규압밀 압축지수를 의미한다. 또한 r과 β는 각각 물질상수이다.
Alonso et al.(1990)와 Gens(1995)에서 제안된 초기 BBM에서는 일정한 흡입력을 갖는 매질의 제하(unloading)와 재하(reloading)에 의한 비체적의 변화가 항복면을 만나기 전까지는 탄성거동을 가정하여 식 (14)와 같이 계산되며, 탄성영역에서 흡입력 변화에 따른 비체적 변화는 식 (15)와 같이 계산된다. 초기 BBM은 과압밀 압축지수(κ)를 상수로 제안하였지만, 이후 식 (16)과 같이 흡입력에 의한 함수의 형태로 적용하였다(Kristensson and Åkesson, 2008; Rutqvist et al., 2011).
| $$d\upsilon=-\kappa\frac{\;dp}p$$ | (14) |
| $$d\upsilon=-\kappa_s\frac{ds}{(s+p_{atm})}$$ | (15) |
| $$\kappa(s)=\kappa(1+s\cdot\alpha_{ps})$$ | (16) |
여기서, κ는 제하와 재하에 대한 υ-lnpʹ곡선에서의 과압밀 압축지수를 의미하며, κs는 흡입력의 함수로 수리적 팽윤지수를 의미하고, patm는 대기압을 의미하는 것으로, 흡입력이 0에 가까워지면서 무한대의 값을 가지게 되는 것을 방지하기 위해 더해주는 값이다. 또한 αps는 물질상수이다.
Fig. 7(b)에 나타나 있는 불포화상태의 선행압밀 응력(preconsolidation stress, p0)과 포화상태의 선행압밀 응력(preconsolidation stress for saturated condition, p0*)의 상관관계를 살펴보면, 응력이 1지점에서 2지점으로 변화하고 흡입력이 2지점에서 3지점으로 변화하면 p0는 p0*와 동일하게 되고, 비체적의 변화는 Fig. 7(a)에 나타나 있듯이 식 (17)로 계산된다.
| $$\upsilon_1+\Delta\upsilon_p+\Delta\upsilon_s=\upsilon_3$$ | (17) |
여기서, ∆υp와 ∆υs는 각각 유효응력과 흡입력의 변화에 의한 비체적 변화를 의미한다.
Fig. 7(a)에 나타나 있는 1지점에서의 비체적(υ1)은 식 (11)로 표현될 수 있으며, 유효응력의 변화에 따른 비체적 변화량(∆υp)은 과압밀 압축지수를 따라 1지점에서 2지점으로 이동하면서 발생하는 비체적 변화량으로 식 (14)에 의해 계산될 수 있다. 흡입력 변화에 의한 비체적 변화량(∆υs)은 2지점에서 3지점으로 이동하면서 발생하게 되는 비체적 변화량으로 식 (15)로 계산되어 식 (17)은 식 (18)로 변환된다. 또한 식 (18)은 ∆υp을 기준으로 식 (19)로 나타낼 수 있다.
| $$N(s)-\lambda(s)\ln\frac{p_0}{p^c}+\kappa\ln\frac{p_0}{p_0^\ast}+\kappa_s\ln\frac{s+p_{atm}}{p_{atm}}=N(0)-\lambda(0)\ln\frac{p_0^\ast}{p^c}$$ | (18) |
| $$\upsilon_1=N(0)-\lambda(0)\ln\frac{p_0^\ast}{p^c}+\kappa\ln\frac{p_0^\ast}{p_0}-\kappa_s\ln\frac{s+p_{at}}{p_{at}}$$ | (19) |
여기서, N(0)는 포화상태일 때, 기준 응력(pc)에서의 비체적을 의미한다.
Fig. 7(a)에서 N(0)와 N(s)의 차이는 팽윤에 의한 비체적 변화와 동일하다고 가정하면 흡입력의 변화로 인한 비체적 변화량(∆υs)은 식 (20)과 같이 표현되고, 이를 식 (19)에 대입하여 정리하면 식 (21)로 표현된다.
| $$N(0)-N(s)=\kappa_s\ln\frac{s+p_{atm}}{p_{atm}}$$ | (20) |
| $$\upsilon_1=N(s)-\lambda(0)\ln\frac{p_0^\ast}{p^c}+\kappa\ln\frac{p_0^\ast}{p_0}$$ | (21) |
3.2 BBM에서의 항복면(yield surface)
3.2.1 흡입력 변화에 따른 항복면 변화
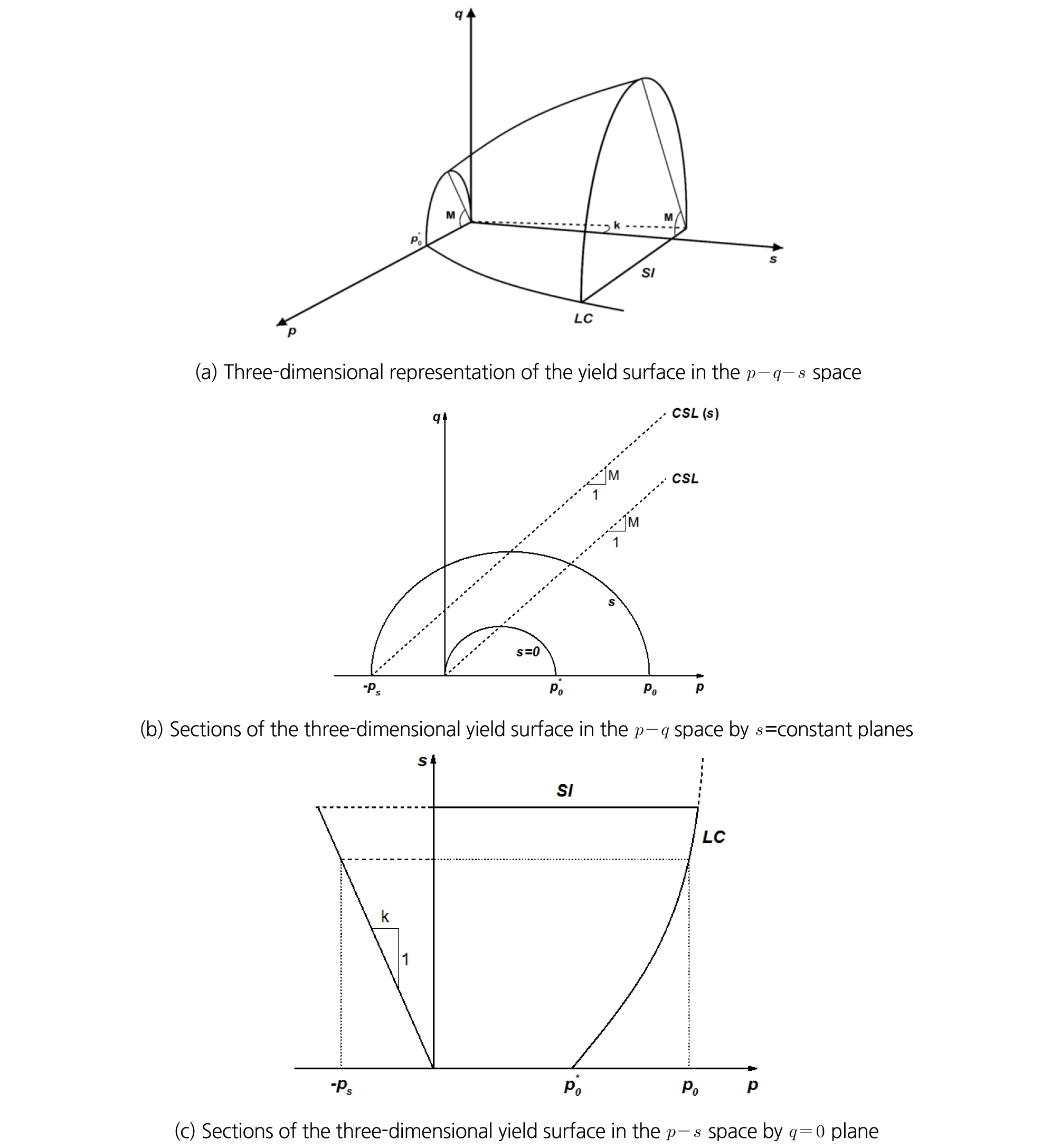
Fig. 8은 p-q-s 공간, p-q 공간, 그리고 p-s 공간에서의 항복면을 나타내고 있는 것으로서, p는 유효응력, q는 편차응력(deviatoric stress), s는 흡입력, M은 p-q 공간에서 한계상태선의 기울기(slope of the critical state line), 그리고 k는 점착력과 관련된 물질 상수(parameter describing the increase of cohesion with suction)를 의미한다.
BBM에서의 항복면은 식 (22)와 같이 정의되고, 완전 포화상태(s=0)의 경우 MCC 모델을 따르며, 흡입력이 증가 할수록 Fig. 8(a)와 Fig. 8(b)에서처럼 항복면의 크기는 증가하게 된다. Fig. 8(c)에 나타나있는 인장강도(tensile strength, ps)의 변화의 경우, 식 (23)에 나타나 있는 것처럼 흡입력과 점착력 관련 물질상수(k)에 비례하는 것으로부터 계산할 수 있다.
| $$q^2-M^2(p+p_s)(p_0-p)=0$$ | (22) |
| $$p_s=-k\cdot s$$ | (23) |
또한 Fig. 8(c)에 나타나 있는 것과 같이 흡입력이 변화함에 따라 변화되는 LC(loading-collapse) 항복면의 크기 변화는 불포화상태의 선행압밀 응력(p0)과 포화상태의 선행압밀 응력(p0*)의 상관관계로부터 계산할 수 있다. 식 (18)은 식 (20)에 의해 식 (24)와 같이 정리될 수 있고, 식 (25)와 식 (26)에 의해 식 (27)로 정리되어 불포화상태의 선행압밀 응력(p0)은 p0*와 pc로부터 계산된다.
| $$\lambda(s)\ln\;\frac{p_0}{p^c}={\lambda(0)\ln\;\frac{p_0^\ast}{p^c}}+\kappa\ln\;\frac{p_0}{p_0^\ast}$$ | (24) |
| $$\lambda(s)\ln\;\frac{p_0}{p^c}-\kappa\ln\;\frac{p_0}{p^c}\;{\lambda(0)\ln\;\frac{p_0^\ast}{p^c}}+\kappa\ln\;\frac{p_0}{p_0^\ast}-\kappa\ln\;\frac{p_0}{p^c}$$ | (25) |
| $$(\lambda(s)-\kappa)\;\ln\;\frac{p_0}{p^c}=(\lambda(0)-\kappa)\;\ln\frac{p_0^\ast}{p^c}$$ | (26) |
| $$\frac{p_0}{p^c}=(\frac{p_0^\ast}{p^c})^\frac{(\lambda(0)-\kappa)}{(\lambda(s)-\kappa)}$$ | (27) |
3.2.2 소성변형에 따른 항복면 변화
BBM에서 유효응력 변화에 따른 체적 변형은 식 (28)로 표현되며, 유효응력(p)이 변화하여 Fig. 7에 나타나 있는 것처럼, 항복면과 만나 p0에 도달하면, 전체 체적변형과 소성변형은 각각 식 (29)와 식 (27)과 같이 계산된다. 또한 식 (27)을 고려하면 식 (30)은 식 (31) 로 표현될 수 있다.
| $$d\varepsilon_{\upsilon p}^e=-d\frac\upsilon\upsilon=\frac\kappa\upsilon\frac{dp}p$$ | (28) |
| $$d\varepsilon_{\upsilon p}^{}=\lambda\frac{(s)}\upsilon\frac{dp_0}{p_0}$$ | (29) |
| $$d\varepsilon_{\upsilon p}^p=d\varepsilon_{\upsilon p}-d\varepsilon_{\upsilon p}^e=\frac{\lambda(s)-\kappa}\upsilon\frac{dp_0}{p_0}$$ | (30) |
| $$d\varepsilon_{\upsilon p}^p=\frac{\lambda(0)-\kappa}\upsilon\frac{dp_{{}_0}^\ast}{p_{{}_0}^\ast}$$ | (31) |
Alonso et al.(1990)가 제안한 BBM에서는 유효응력 변화뿐만 아니라, Fig. 8(c)에 나타나 있는 흡입력의 증가(suction increase, SI)로 인한 소성변형이 발생할 수 있다. 불포화토의 흡입력이 지금까지 겪어온 최대 흡입력(s0)보다 작은 경우에는 탄성 거동을 보이기 때문에 탄성영역에서의 변형률(dεvse)은 식 (32)와 같이 계산되지만, 흡입력이 최대 흡입력(s0)을 넘어서게 되면 전체 변형률(dεvs)과 소성변형률(dεvsp)은 각각 식 (33)과 식 (34)로 계산된다.
| $$d\varepsilon_{\upsilon s}^e=\frac{\kappa_s}\upsilon\frac{ds}{(s+p_{at})}$$ | (32) |
| $$d\varepsilon_{\upsilon s}=\frac{\kappa_s}\upsilon\frac{ds_0}{(s_0+p_{at})}$$ | (33) |
| $$d\varepsilon_{vs}^p=d\varepsilon_{vs}^{}+d\varepsilon_{vs}^e=\frac{\lambda_s-\varepsilon_s}\upsilon\frac{ds_0}{(s_0+p_{at})}$$ | (34) |
BBM에서의 유효응력 및 흡입력의 변화에 따른 소성변형률 변화(dεvp)는 식 (35)와 같이 표현될 수 있으며, 소성변화에 따른 두 항복면의 경계인 LC와 SI는 식 (36) 그리고 식 (37)과 같은 경화법칙(hardening law)을 따른다.
| $$d\varepsilon_v^p=d\varepsilon_{vp}^p+d\varepsilon_{vs}^p$$ | (35) |
| $$\frac{dp_0^\ast}{p_0^\ast}=\frac\upsilon{\lambda(0)-\kappa}d\varepsilon_v^p$$ | (36) |
| $$\frac{ds_0}{s_0}=\frac\upsilon{\lambda_s-\kappa_s}d\varepsilon_v^p$$ | (37) |
3.2.3 온도 변화에 따른 항복면 변화
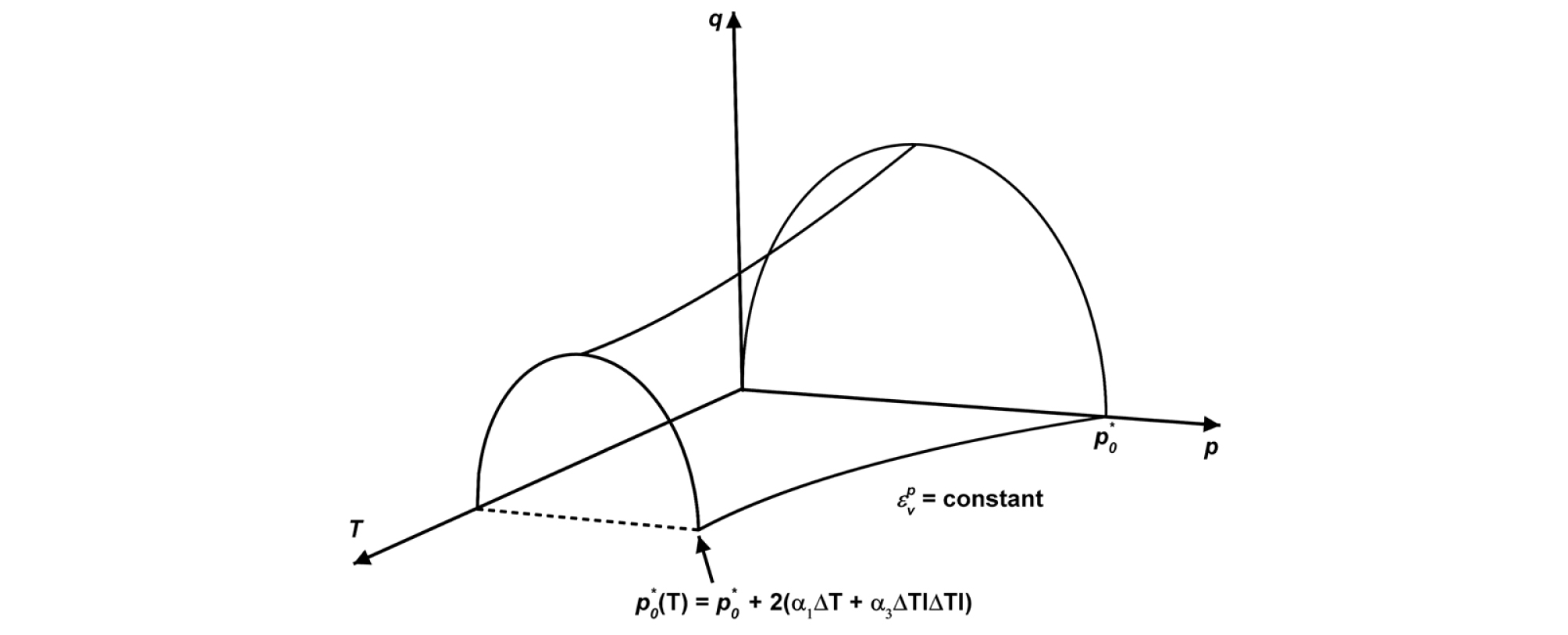
탄소성 모델(elasto-plastic model)인 BBM은 온도(T) 변화에 따른 항복면의 변화를 식 (38)과 같이 고려하여 열・탄소성 모델(thermo-elasto-plastic model)로 새롭게 제안되었다(Gens, 1995). 열・탄소성 BBM은 온도가 증가함에 따라 항복면이 작아지는 특징을 갖는 모델로서, 항복면을 삼차원 pʹ-q-T 공간에 도시하면 Fig. 9와 같이 표현이 된다.
| $$p_0^\ast(T)=p_0^\ast+2(\alpha_1\bigtriangleup T+\alpha_3\bigtriangleup T\vert\bigtriangleup T\vert)$$ | (38) |
여기서 , α1 그리고 α3는 물질상수(parameters that relate preconsolidation stress and temperature changes)를 의미하고, ∆T는 온도변화를 의미한다.
4. 결 언
BBM은 흡입력 및 온도 변화에 따른 불포화 토질의 역학적 거동 변화를 모사할 수 있기 때문에 고준위방사성폐기물 처분시스템에서 공학적방벽재로 고려되고 있는 벤토나이트 완충재의 열-수리-역학적 복합거동을 잘 모사하는 것으로 알려져 있으며, 고준위방사성폐기물 처분시스템 설계 및 성능평가에 많이 사용되고 있다. 하지만, 국내 암반 및 지반공학자들에게는 잘 알려져 있지 않기 때문에 본 고에서 열-탄소성 모델인 BBM을 소개하였다.
BBM은 흡입력과 온도를 고려할 수 있도록 MCC 모델을 확장하여 제안된 열-탄소성 모델이기 때문에, 본 고에서는 먼저 MCC 모델에서의 응력변화에 따른 비체적 계산방법과 MCC 모델에서의 경화법칙을 간략하게 소개하였다. 이후, MCC 모델과는 달리 BBM에서 흡입력의 함수로 표현되는 정규압밀 압축지수와 과압밀 압축지수를 이용한 비체적 계산방법과 흡입력 변화와 소성변형에 따른 항복면 변화 특징에 대해 상세히 소개하였다. 또한, 본 고에서는 탄-소성 버전의 BBM 뿐만 아니라, 온도 변화에 따른 항복면 변화를 고려한 열-탄소성 버전의 BBM에 대해서도 자세히 살펴보았다. 본 고에서 소개된 BBM은 앞으로 한국형 표준처분시스템의 성능평가와 복층처분장과 같은 대안 처분시스템의 설계 및 성능평가뿐만 아니라, 다양한 지반공학 관련 모델링에 적용될 수 있을 것으로 판단된다.