1. 서 론
2. 암반 불연속면 내로 압축 벤토나이트 침투 모사 모델 현황
3. Bingham 유체 모델에 의한 압축 벤토나이트 침투 모델링
3.1 벤토나이트 최대 침투깊이
3.2 천이상태 벤토나이트의 침투
4. 압축 벤토나이트 침투관련 물성
4.1 압축 벤토나이트 팽윤압
4.2 압축 벤토나이트 점도
4.3 압축 벤토나이트 항복강도
5. 압축 벤토나이트 침투 평가
5.1 입력인자
5.2 최대 침투깊이
5.3 시간 경과에 따른 벤토나이트의 침투
6. 결 론
1. 서 론
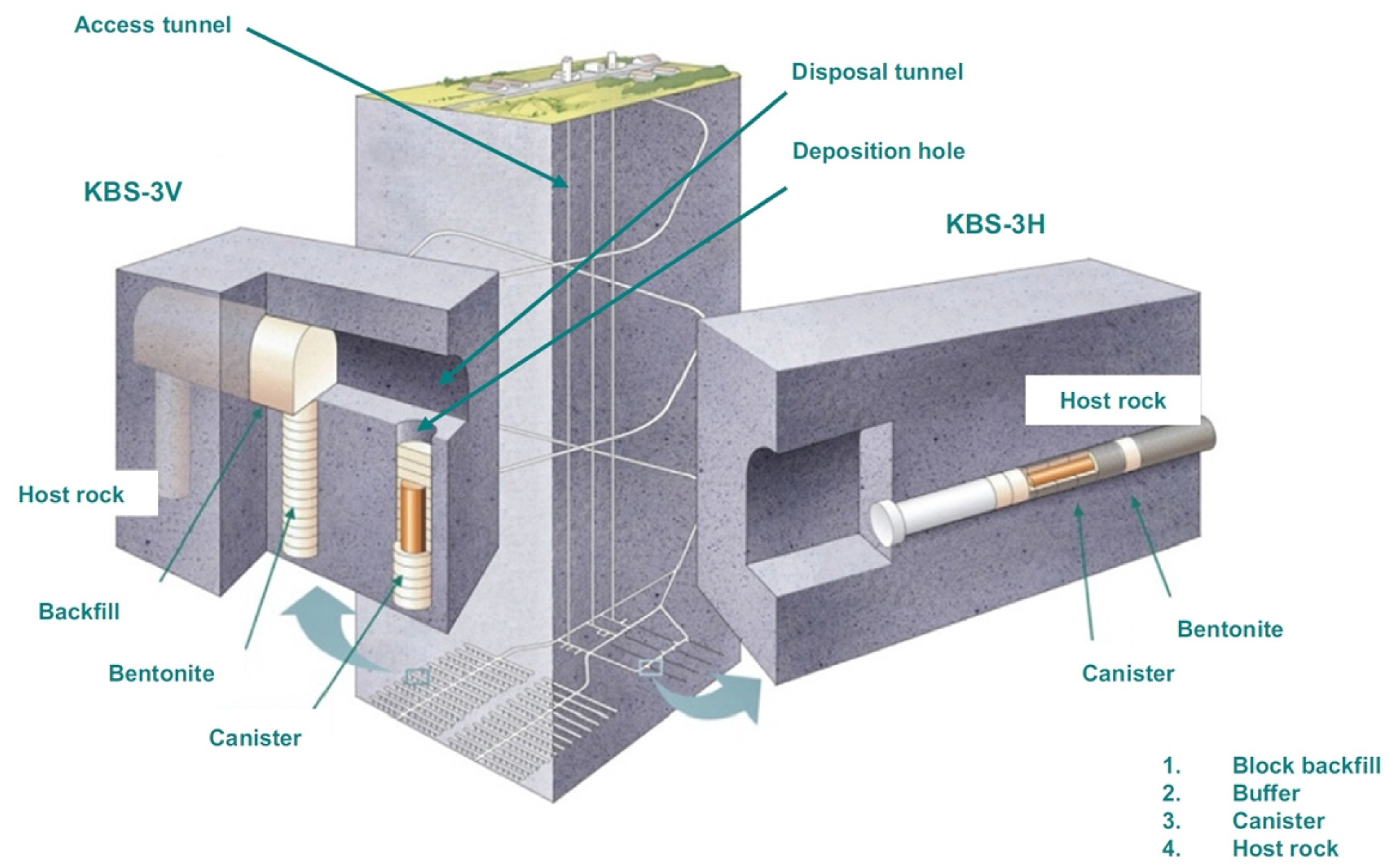
사용후핵연료 처분방식 중 가장 유력한 방식은 공학적방벽과 자연방벽으로 이루어진 다중방벽 개념을 이용한 심층처분방식이다. 이 방식에서는 지하 수백 미터 깊이에 위치한 균열 및 절리가 적고, 안정된 암반에 굴착된 처분터널 바닥에 수직으로 혹은 처분터널 벽에 수평으로 처분공을 굴착하고, 그 속에 사용후핵연료를 밀봉한 처분용기를 넣은 후 처분용기와 처분공 암반 내벽 사이의 공간을 압축 벤토나이트 완충재로 충전시킨다(Fig. 1). 공학적방벽재인 압축 벤토나이트 완충재의 가장 큰 역할은 주위 암반으로부터 지하수가 침투하는 것을 저지하고, 사용후핵연료로부터 방사성핵종이 누출된 경우에는 방사성핵종이 처분장 주위 암반으로 유출되는 것을 저지하는 것이다. 이외에 압축 벤토나이트는 유연성을 지니고 있어, 처분공에 가해진 응력이나 변위를 근계암반으로 분산시켜 처분공이 국부적으로 큰 응력을 받는 것을 방지하는 역학적 기능도 가지고 있다.
심부지하에 처분터널과 처분공을 굴착하게 되면, 굴착 시 가해지는 충격으로 인해 암반의 물성과 상태가 초기 값과 달라지는 영역이 형성된다. 굴착에 의한 충격과 응력 재분포(stress redistribution)로 인해 암반의 열적, 수리적, 역학적 및 화학적 물성이 변화되는 영역을 굴착손상영역(excavation damaged zone, EDZ)이라고 한다. 고준위방사성 처분장에서의 굴착손상영역은 처분장의 장기적인 운영, 안정성 및 안전성에 있어 매우 중요한 요소이기 때문에 전 세계의 많은 지하처분연구시설에서 굴착손상영역의 발생원인, 주요영향인자 및 그 규모에 대해 많은 연구를 수행하였다. 국내에서는 한국원자력연구원 부지 내에 위치한 지하처분연구시설(KAERI Underground Research Tunnel, KURT)를 활용한 연구들이 있으며(Kwon et al., 2009; Lee et al., 2011), 국외 연구사례에 대해서는 Lee et al.(2011), Lee(2012), 그리고 Park and Kwon(2017)에 잘 정리되어 있다.
처분터널에 굴착된 처분공의 내벽에는 자연 절리와 굴착과정에서 형성된 굴착손상영역에서의 균열과 같은 다수의 불연속면들이 존재하며, 심층처분장이 폐쇄되면 이 불연속면을 통해 처분공 주위 암반에 존재하는 지하수가 처분공 내로 침투(penetration)하게 된다. 처분공 내로 침투한 지하수는 처분공에 설치되어 있는 압축 벤토나이트 완충재를 포화시키게 되며, 지하수로 포화된 벤토나이트 완충재는 팽윤하여 처분공 내벽에 팽윤압(swelling pressure)을 가하게 된다. 이 팽윤압으로 인해, 완충재 재료인 압축 벤토나이트의 일부가 처분공 내벽에 존재하는 절리 또는 미세 균열 내로 밀려들어가게 된다. 이 현상을 암반 불연속면으로의 벤토나이트 침투라 한다.
처분공 내벽의 암반 불연속면 안으로 벤토나이트가 침투하는 현상은 심층처분장의 성능에 긍정적인 영향을 미칠 수도 있고, 부정적인 영향을 미칠 수도 있다. 긍정적인 영향으로는 암반의 불연속면을 메워 처분공 주위 근계암반의 수리전도도를 감소시키거나, 열전도도를 증가시킬 수 있다. 부정적인 영향으로는 암반 불연속면 안으로 침투한 압축 벤토나이트의 말단에서 지하수에 의한 침식이 일어나 벤토나이트 완충재가 손실되고, 벤토나이트 콜로이드가 형성되어 처분안전성에 악 영향을 미칠 수 있다는 점이다. 또한, 암반 불연속면 사이에 벤토나이트가 존재하면 암반의 전단강도가 낮아져 근계암반의 역학적 건전성이 저하될 수 있다. 암반 불연속면 안으로의 벤토나이트 침투 현상이 심층처분장 성능에 미치는 영향은 벤토나이트가 침투하는 깊이가 얼마인가, 또 침투에 걸리는 시간이 얼마인가에 따라 결정된다.
이 논문에서는 처분공에 설치된 압축 벤토나이트 완충재가 처분공 내벽에 형성된 손상영역에 존재하는 불연속면으로 침투하는 현상을 조사하고, 이 현상을 모사하기 위해 제안된 기존모델의 특성을 분석하였다. 이를 바탕으로 심층처분장 처분공 내벽에 형성된 손상영역 불연속면과 완충재의 특성에 따른 압축 벤토나이트의 침투거리와 침투속도를 추정할 수 있는 정량적 모델을 제시하고자 하였다.
2. 암반 불연속면 내로 압축 벤토나이트 침투 모사 모델 현황
Birgersson et al.(2009)은 압축 벤토나이트가 암반 불연속면 내로 침투하는 현상을 모사하기 위하여 힘-평형 모델을 제안하였다. 이 모델에서는 압축 벤토나이트와 불연속면의 표면 사이에 작용하는 전단응력을 식 (1)로 나타내었다.
| $$\tau=\sigma\;\tan\;\varnothing$$ | (1) |
여기서, τ는 암반 불연속면에 작용하는 전단응력을 의미하고, σ는 압축 벤토나이트의 팽윤압이며 ∅는 압축 벤토나이트와 암반 불연속면 사이의 마찰각(friction angle)을 의미한다.
압축 벤토나이트와 불연속면 사이의 마찰각은 압축 벤토나이트의 밀도와 포화도에 따라 달라져, 압축 벤토나이트의 밀도가 감소하거나, 포화도가 증가하면, 마찰각은 감소한다. 벤토나이트가 암반 불연속면 내로 침투할수록, 전단(front)에서 벤토나이트의 건조밀도가 감소하면 마찰각도 감소하고, 겔(gel) 상태를 거쳐 졸(sol) 상태로 변해갈수록, 마찰각의 감소 정도는 급격해진다. 그러나 불연속면 내로 침투하는 매질의 상태 변화에 따른 물성 변화를 모두 고려하여 모델링하는 것이 현실적으로 어렵기 때문에, 대부분의 지질공학적 문제에서 전 응력장(stress field)에서 매질의 물성이 일정하게 유지된다고 가정하는 것이 일반적이다. 따라서 이 모델에서도 불연속면 내로 침투하는 벤토나이트의 마찰각이 일정하게 유지된다고 가정하였다(Birgersson et al., 2009; Borgesson et al., 2018).
벤토나이트 미소 구간에서 방사 방향으로의 힘 평형방정식은 식 (2)와 같고, 처분공 반경 r1에서 특정 거리 r2까지 적분하면 일 때, 즉 침투 깊이(I = r - r1)가 작은 경우에는 식 (3)으로 나타낼 수 있다(Birgersson et al., 2009).
| $$-\frac{dr}r-\frac{d\sigma}\sigma=dr\frac{2\;\tan\;\phi}b$$ | (2) |
| $$\sigma=\sigma_1e^{-2\tan\phi(\frac Ib)}$$ | (3) |
여기서, σ는 암반 불연속면 내의 거리 r - r1에서 침투한 벤토나이트의 팽윤압이고, σ1는 처분공 내벽에 작용하는 압축 벤토나이트 팽윤압이며, b와 ∅는 각각 암반 불연속면의 폭(aperture)과 압축 벤토나이트와 암반 불연속면 사이의 마찰각을 의미한다.
식 (3)은 암반 불연속면 내로 침투한 벤토나이트의 팽윤압, 처분공 압축 벤토나이트 완충재의 팽윤압, 암반 불연속면의 폭, 벤토나이트 침투 깊이 사이의 관계를 나타내는 식으로, 암반 불연속면 내로 벤토나이트가 침투하는 속도나 침투 시간 등은 고려하지 않고, 단지 평형에 도달했을 때의 관계를 나타낸다. 이 힘-평형 모델은 압축 벤토나이트를 고체로 간주하기 때문에 암반 불연속면을 침투한 벤토나이트와 암반 불연속면 사이의 마찰에 의한 에너지 손실이 과다하게 평가되어 벤토나이트의 침투깊이가 지나치게 과소평가된다. 또 식 (3)은 압축 불연속면 내로의 침투에 따른 벤토나이트 팽윤압의 감소 정도만을 보여줄 뿐, 언제 벤토나이트의 침투가 정지되는가에 대한 정보를 제공해주지 못하기 때문에, 실제 암반 불연속면 내로 벤토나이트의 침투거리를 계산하는데 사용하기 곤란하다.
Svoboda et al. (2013)는 압축 벤토나이트가 팽윤에 의해 불연속면 내로 침투하는 힘과 불연속면에서의 마찰력이 평형을 이루는 지점까지 벤토나이트가 침투한다고 가정하여 일차원 평행 불연속면에 대해 위와 유사한 힘-평형 모델을 유도하였다. 이 모델에서는 암반 불연속면 내로의 압축 벤토나이트의 최대 침투깊이(Imax)를 식 (4)로 나타내었다(Svoboda et al., 2013).
| $$I_\max=\frac{bc_1(\rho_{d\max}-\rho_{d\min})}{2\;\tan\;(\phi)}$$ | (4) |
여기서, b는 암반 불연속면의 폭, c1는 상수, ρdmax 및 ρdmin는 각각 처분공에서의 벤토나이트 건조밀도 및 암반 불연속면 내로 침투한 벤토나이트 말단에서의 건조밀도이고, ∅는 마찰각이다.
식 (4)를 이용하여 압축 벤토나이트의 최대 침투깊이를 추정하기 위해서는 벤토나이트 말단에서의 건조밀도(ρdmin)와 압축 벤토나이트와 암반 불연속면 사이 마찰각(∅)에 대한 정보가 필요하나, 이에 대한 언급이 없고, 실제 이 식을 이용하여 벤토나이트 최대 침투깊이를 추정하지 않았다(Svoboda et al., 2013).
암반 불연속면 내로 침투하는 압축 벤토나이트가 뉴턴 유체(Newtonian fluid)이고 층류(laminar flow)라고 가정하면, 암반 불연속면 내로 압축 벤토나이트가 침투하는 현상은 Poiseuille 방정식에 의해 식 (5)로 표시될 수 있다(Grindrod et al., 1999, Kanno and Iwata, 2004, Neretnieks et al., 2009).
| $$\overline{u_b}=-\frac{b^2}{12\mu_b}\frac{d\sigma_s}{dI}$$ | (5) |
여기서, 와 μb는 각각 벤토나이트의 평균 유속과 벤토나이트 점도(viscosity)이며, b는 불연속면의 폭, I는 거리, 그리고 σs는 벤토나이트의 팽윤압을 의미한다.
식 (5)에서는 벤토나이트가 침투됨에 따라 벤토나이트의 밀도와 팽윤압이 감소하여, 벤토나이트의 팽윤압이 사라지는(σs = 0) 지점에서, 벤토나이트의 침투가 중지된다. 벤토나이트의 밀도가 감소하면 점도도 감소하나, 수학적 모델링을 용이하게 만들기 위하여 불연속면 내로 침투하는 벤토나이트의 점도가 일정하게 유지된다고 가정하였다. Poiseuille 방정식은 정상상태(steady state)에 있는 뉴턴 유체의 층류흐름에서 압력 강하(pressure drop)를 나타내는 식이므로, 시간 경과에 따른 벤토나이트의 침투깊이에 대한 정보를 얻을 수 없고, 실제 이 식을 사용하여 암반 불연속면 내로의 압축 벤토나이트의 침투깊이를 추정한 사례가 없다.
Kanno and Iwata(2004)는 Poiseuille 방정식으로부터 암반 불연속면에서의 벤토나이트 고상 확산 계수(solid phase diffusion coefficient)를 구한 다음, 이 고상 확산 계수를 사용한 확산방정식을 이용하여 암반 불연속면에서 벤토나이트 겔의 이동을 모사하였다. 즉 암반 불연속면을 통한 벤토나이트의 침투는 식 (6)과 같은 확산방정식으로 모사되었다.
| $$\frac{\partial\theta_b}{\partial t}=\nabla\;\bullet\;\left[D_b(\theta_b)\;grad\;\theta_b\right]$$ | (6) |
여기서, θb는 벤토나이트 고상 부피분율(= )이며, 이 때 Vbs는 벤토나이트 고상 부피, V는: 벤토나이트 겔의 전체 부피이다. t와 Dbs는 각각 시간과 벤토나이트 고상확산계수를 나타낸다.
이 확산방정식의 경계조건으로, 침투한 벤토나이트 전단(front)의 함수비가 벤토나이트의 액성한계와 같다고 가정하였다. 식 (6)을 이용하여 암반 불연속면 내로 벤토나이트 겔이 침투하는 현상을 모사한 결과, 벤토나이트의 침투속도가 지나치게 크게 나타났으며, 이는 소성체인 압축 벤토나이트를 뉴턴 유체로 가정한데서 기인하는 것으로 추정된다.
Kanno et al.(1999)은 암반 불연속면 내로 벤토나이트 겔의 침투실험을 수행하고, 실험에서 얻은 데이터를 이용하여, 벤토나이트 겔의 침투깊이와 경과시간 사이의 관계를 식 (7)과 같은 실험식으로 나타내었다.
| $$I=A\sqrt t$$ | (7) |
여기서, I는 벤토나이트 겔의 침투깊이, t는 경과시간이며 A는 불연속면의 폭 b와 벤토나이트 함량 비에 의존하는 비례계수이다. Tanai and Matsumoto(2008)는 A를 불연속면의 폭 b와 유효점토밀도(effective clay density) 함수로서 제시하였다.
3. Bingham 유체 모델에 의한 압축 벤토나이트 침투 모델링
고분자 용액이나 겔에서는 유체의 흐름이 일어날 때, 입자 사이의 상호작용에 의해 형성되어 있던 유체의 3차원 구조가 파괴되기 때문에 전단응력과 전단속도 사이에 뉴턴 유체와 같은 비례관계가 성립되지 않는 비 뉴턴 유체(non-Newtonian fluid)가 발생한다. 비 뉴턴 유체의 일종인 Bingham 유체는 외력이 가해지면 처음에는 고체처럼 거동하다가, 내부 전단응력(internal shear stress)이 유체의 항복강도(yield strength)를 초과하게 되면, 점성 유체(viscous flow)처럼 거동한다(Fig. 2). 따라서 Bingham 유체의 유동은 유체의 항복강도(yield strength)와 소성 점도(plastic viscosity)에 의해 결정된다. 벤토나이트 입자가 수용액 중에 골고루 분산되어 있는 벤토나이트 졸이나 농도가 낮은 겔은 점도(viscosity)가 낮아 뉴턴유체로 취급될 수 있으나, 수용액 중의 벤토나이트 입자 농도가 높은 겔 상태로 되면, 비 뉴턴 유체의 특성이 나타난다.
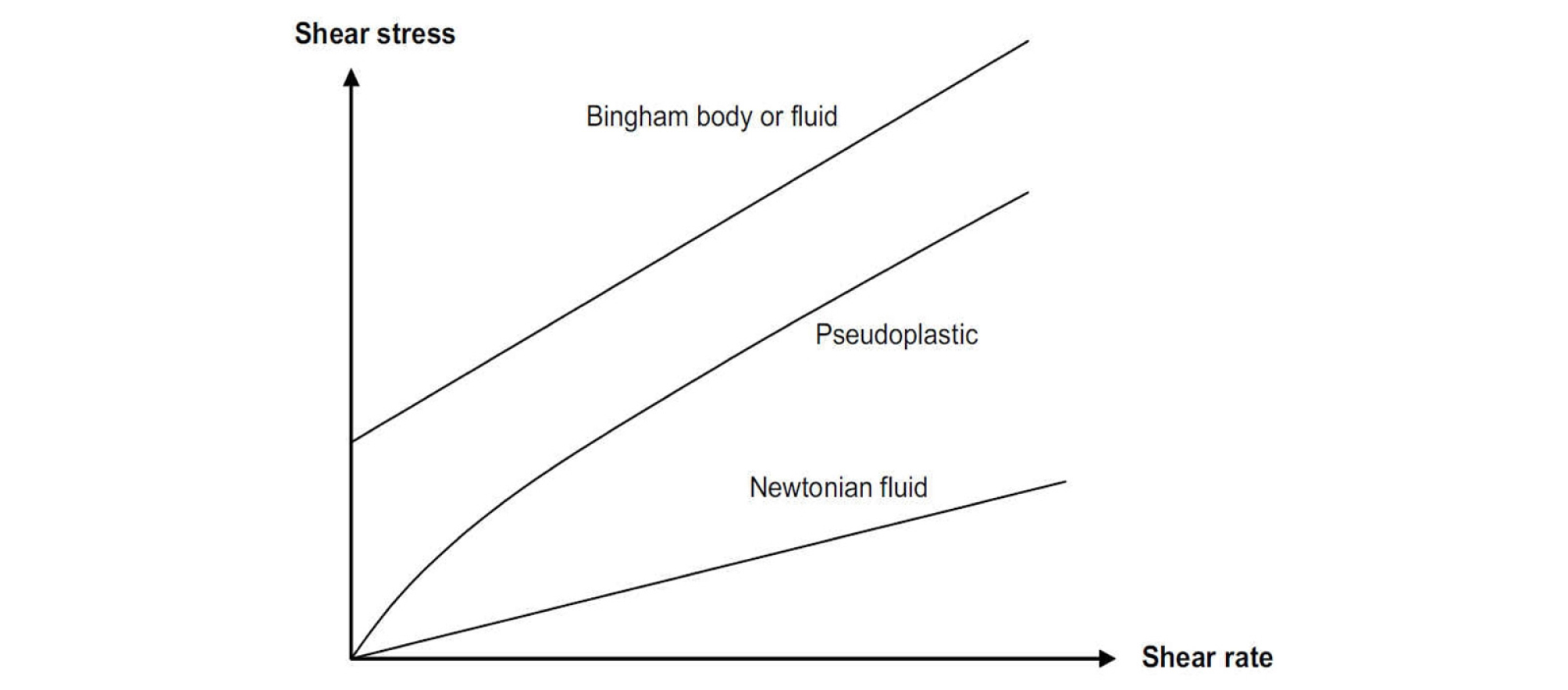
Fig. 2.
Schematic diagram illustrating relations between shear stress and shear rate governing Newtonian, Pseudoplastic (power-law) and Bingham flow behaviour (Apted et al., 2010)
Pusch (1983)는 벤토나이트의 함량이 2%인 묽은 벤토나이트 겔은 뉴턴 유체의 거동을 보이나, 벤토나이트의 함량이 5%로 증가하면 벤토나이트 겔은 비 뉴턴 유체인 Bingham 유체의 성질을 보인다고 보고하였다. 따라서 벤토나이트의 함량이 아주 높은 압축 벤토나이트는 항복강도라 불리는 문턱 값(threshold value) 이하의 전단응력에서는 고체처럼 거동하여 전단이 일어나지 않다가, 항복강도 이상의 전단응력이 가해지면 점성유체(viscous flow)로 거동하는 Bingham 유체의 특성을 가질 것이라고 추정할 수 있다. 따라서 본 연구에서는 처분공에 설치된 압축 벤토나이트 완충재가 지하수에 의해 포화된 후, 팽윤에 의해 처분공 내벽에 존재하는 손상영역 불연속면 내로 침투하는 현상을 평행 평판 암반 불연속면을 통한 Bingham 유체의 이동으로 모사하고자 한다.
3.1 벤토나이트 최대 침투깊이
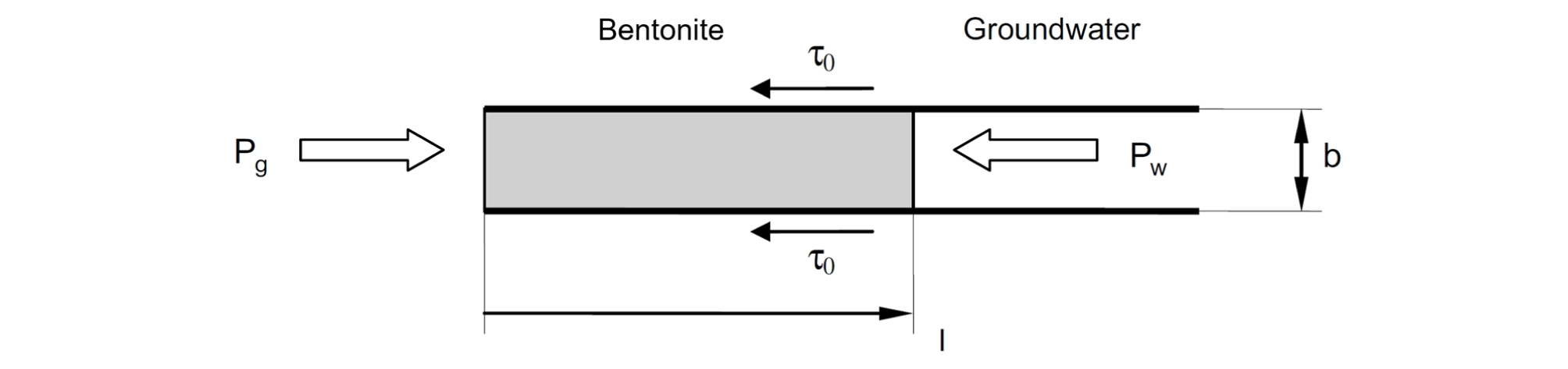
처분공에 설치되어 있는 벤토나이트 완충재가 지하수로 포화되어, 발생하는 팽윤압이 압축 벤토나이트의 항복강도를 초과하여 식 (8)의 조건이 만족될 때, 벤토나이트가 손상영역 불연속면 내로 침투한다.
| $$\frac{\sigma_s}Ib\;>\;2\;\tau_o$$ | (8) |
여기서, I는 압축 벤토나이트의 침투깊이, σs는 압축 벤토나이트의 팽윤압, b는 손상영역 불연속면의 폭, 그리고 τo는 압축 벤토나이트의 항복강도를 의미한다.
압축 벤토나이트가 손상영역의 불연속면 내로 침투하는 거리는 불연속면의 폭에 따라 달라지며, 벤토나이트의 항복강도에 좌우된다. 압축 벤토나이트가 암반 불연속면 내로 침투할수록, 전단(front)에서는 벤토나이트의 건조밀도가 감소하여 항복강도도 감소한다. 그러나 불연속면 내로 침투하는 매질의 상태 변화에 따른 물성의 변화를 모두 고려하여, 모델링하기 어렵기 때문에, 대부분의 지질공학적 문제에서 응력장(stress field) 전체에서 매질의 물성이 일정하게 유지된다고 가정하는 것이 일반적이다. 여기서도 손상영역 불연속면 내로 침투하는 압축 벤토나이트의 항복강도가 일정하게 유지된다고 가정하였다.
압축 벤토나이트 완충재가 처분공 내벽의 손상영역 불연속면 내로 침투하는 과정에서, 불연속면에 대한 벤토나이트의 내부 전단응력이 벤토나이트의 항복강도와 균형을 이룰 때 벤토나이트의 전단이 더 이상 침투하지 못하고 정지한다(Fig. 3). 그리고 압축 벤토나이트의 물성이 시간에 무관하다고 가정하였으므로, 불연속면 폭이 b로 일정한 평행평판 암반 불연속면 내로 벤토나이트가 침투할 수 있는 최대깊이는 식 (9)로 나타낼 수 있다(Gustafson et al., 1996; Kobayashi and Stille, 2007).
| $$I_\max=(\frac{P_g-P_w}{2\tau_o})\;b$$ | (9) |
여기서, Imax는 벤토나이트 최대 침투깊이이고, Pg와 Pw는 각각 압축 벤토나이트 완충재의 총 압력(팽윤압과 지하수압의 합)과 지하수압을 의미하며, τo와 b는 각각 항복강도와 손상영역 불연속면의 폭을 의미한다.
3.2 천이상태 벤토나이트의 침투
손상영역 암반 불연속면 내로 압축 벤토나이트 완충재가 침투하는 현상은 폭이 일정한 평행한 평판 불연속면 내에서의 Bingham 유체의 이동으로 모사되었다. Bingham 유체에서는 전단응력(τ)과 항복강도(τo)의 관계는 식 (10)과 같다. Bingham 유체에서는 전단응력이 항복강도보다 작으면 속도구배(velocity gradient)가 영이고, 유체의 내부전단응력이 유체의 항복강도보다 커질 때만 유동이 일어난다.
| $$\tau\;=\;-\mu_g\frac{du(z)}{dz}+\tau_o\;\;\;\;\;\;\;\;\;\left|\tau\right|\;>\;\tau_o$$ | (10) |
여기서, μg는 Bingham 유체의 소성점도(plastic viscosity)이고, u는 유속이다.
Bingham 유체 모델에서는 처분공 내벽에 포화 압축 벤토나이트의 팽윤압이 일정하게 유지된다고 가정한다. 실제 처분공에서 손상영역의 불연속면 내로 침투하는 벤토나이트의 양은 처분공에 존재하는 압축 벤토나이트 완충재의 총량에 비해 매우 작으므로, 손상영역의 불연속면 입구에 가해지는 벤토나이트의 팽윤압이 일정하다고 가정하여도 큰 무리가 없다.
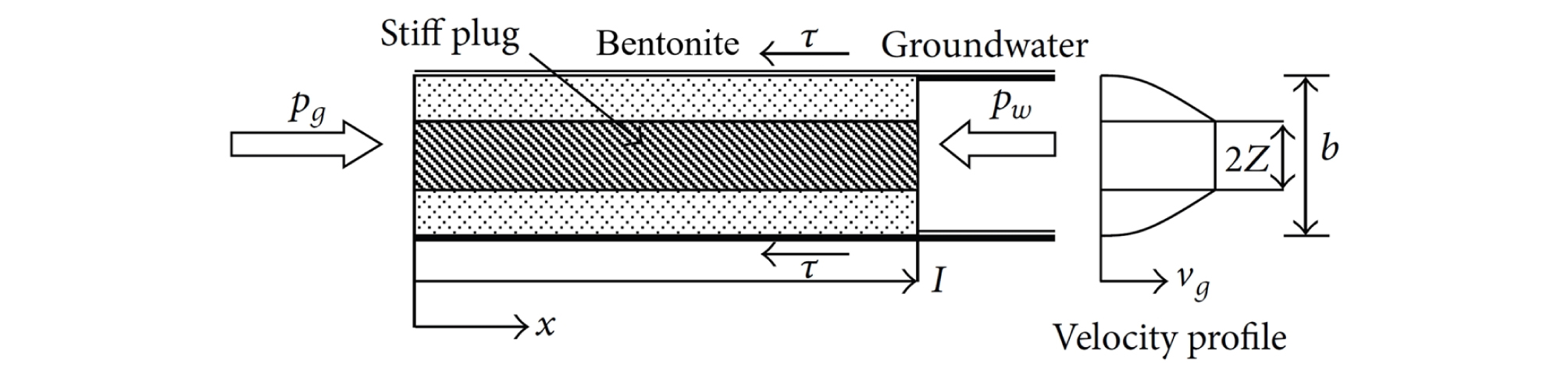
손상영역의 불연속면에서 흐르는 압축 벤토나이트 완충재의 유로 중앙 부분에는 Fig. 4에 나타나 있는 것처럼, 벽면으로부터 거리에 따른 전단응력의 변화가 없이 고체처럼 거동하는 직경이 2 Z인 경화플러그(stiff plug)가 형성되어 있고, 그 플러그 주위를 소성유동대(plastic flow zone)가 둘러싸고 있으며, 암반 불연속면을 통해 흐르는 압축 벤토나이트의 흐름은 층류(laminar flow)라고 가정한다(Gustafson et al., 2013). 손상영역의 불연속면 내에서는 x 방향을 제외한 모든 방향의 유속이 영이고, 부피요소(volume element) dxdydz를 고려하면 부피요소에서 질량과 운동량이 보존되어야 하므로 정상상태(steady state)의 비압축성 층류(laminar flow)의 연속방정식(equation of continuity)과 Navier Stokes 방정식은 식 (11)과 같이 간단한 형태로 표시할 수 있다(Bird, 2002).
| $$\frac{\partial\Gamma_{xx}}{\partial x}+\frac{\partial\Gamma_{xz}}{\partial z}=0$$ | (11) |
여기서, Γ는 유체 요소에 작용하는 응력텐서(stress tensor)이다.
Γ에 압력(P)와 전단응력 τ(z)를 도입하고(Hässler, 1991), 식 (12)과 식 (13)을 이용하면, 식 (11)은 식 (14)와 같이 나타낼 수 있다.
| $$\Gamma_{xx}=P$$ | (12) |
| $$\Gamma_{xz}=\tau(z)$$ | (13) |
| $$\frac{d\tau(z)}{dz}=-\frac{dP}{dx}$$ | (14) |
식 (14)를 z에 대해 적분하고, z=0 에서 τ=0 (symmetry), z=Z 에서 τ=τo (항복강도)인 경계조건들을 이용하면 식 (15)로 표현할 수 있다.
| $$\tau_o=-Z\frac{dP}{dx}$$ | (15) |
식 (10)을 식 (14)에 대입하면 식 (16)과 같고, 경계조건은 식 (17)과 식 (18)과 같다.
| $$\frac\partial{\partial z}(\mu_g\frac{du(z)}{dz}-\tau_o)\;=\;\frac{dP}{dx}$$ | (16) |
| $$u(z)=0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;z=\frac b2$$ | (17) |
| $$\frac{du}{dz}=0,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;z=Z$$ | (18) |
위 식을 적분하여 정리하고, I(t)를 시간 t에서 불연속면 내로 침투한 압축 벤토나이트 전단(front)의 위치라고 하면, 폭이 b인 손상영역의 수평 불연속면 내로 침투하는 벤토나이트의 속도()는 식 (19)와 같이 표현될 수 있고, Z는 식 (20)과 같다(Hässler, 1991).
| $$\frac{dI}{dt}\;=-\frac{dP}{dx}\;\frac{b^2}{12\mu_g}\lbrack1-3\frac Zb+4{(\frac Zb)}^3\rbrack$$ | (19) |
| $$Z=\tau_o\;\left|\frac{dP}{dx}\right|^{-1}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;Z\;\prec\;\frac b2$$ | (20) |
여기서, b, μg, 그리고 τo는 각각 암반 불연속면의 폭, 압축 벤토나이트의 점도, 그리고 압축 벤토나이트의 항복강도이다.
평행유동(parallel flow)을 가정하고 압축 벤토나이트의 점도가 물의 점도보다 훨씬 크면, 압력구배는 식 (21)과 같이 단순화될 수 있고(Gustafson et al., 2013), 식 (9), (20) 및 (21)로부터 식 (22)가 도출된다.
| $$\frac{dP}{dx}=-\frac{\triangle P}I$$ | (21) |
| $$\frac{2Z}b=-\frac I{I_\max}$$ | (22) |
또한, 상대침투깊이(relative penetration depth), ID를 식 (23)과 같이 정의하면 ID를 이용하여 식 (19)를 식 (24)와 같이 간단히 나타낼 수 있다(Gustafson et al., 2013).
| $$I_D=\frac I{I_\max}$$ | (23) |
| $$\frac{dI_D}{dt}=\frac{{(\tau_o)}^2}{6\mu\triangle P}\;\bullet\;\frac{2-3\;I_D+{(I_D)}^3}{I_D}$$ | (24) |
이와 유사하게 특성시간(characteristic time), to와 상대침투시간(relative penetration time), tD를 식 (25)와 같이 정의하면, 식 (24)는 식 (26)과 같이 나타낼 수 있다.
| $$t_o=\frac{6\triangle P\;\mu_g}{\tau_o^2}$$ | (25) |
| $$\frac{dt_D}{dt_D}=\frac{I_D}{2-3\;I_D+{(I_D)}^3}=\frac{I_D}{(2+I_D)\;{(I-I_D)}^2}$$ | (26) |
식 (26)을 적분하면, 식 (27)과 같이 tD를 ID의 함수로서 나타낸 해를 구할 수 있다(Gustafson et al., 2013). 이 해에서 tD = 0에서 ID = 0이다. tD의 함수로 나타낸 ID는 Fig. 5에 나타나 있다.
| $$t_D=\frac{I_D}{3(I-I_D)}+\frac29\ln\;\lbrack\;\frac{2(I-I_D)}{2+I_D}\rbrack$$ | (27) |
식 (27)로부터 ID에 대한 해가 명료하게 구해지지 않기 때문에 Gustafson and Stille (2005)는 자연대수 함수의 급수 전개와 적절한 조작을 통해 식 (27)의 근사식을 식 (28)과 같이 제안하였다.
| $$I_D\;\approx\;\sqrt{\frac{t_D^2}{4(1+t_D)}+\frac{2t_D}{1+t_D}}-\frac{t_D}{2(1+t_D)}$$ | (28) |
여기서, 새로운 파라미터 를 도입하면, ID는 θ의 함수로서 식 (29)로 나타낼 수 있다.
| $$I_D\;=\sqrt{\theta^2+4\theta}-\theta$$ | (29) |
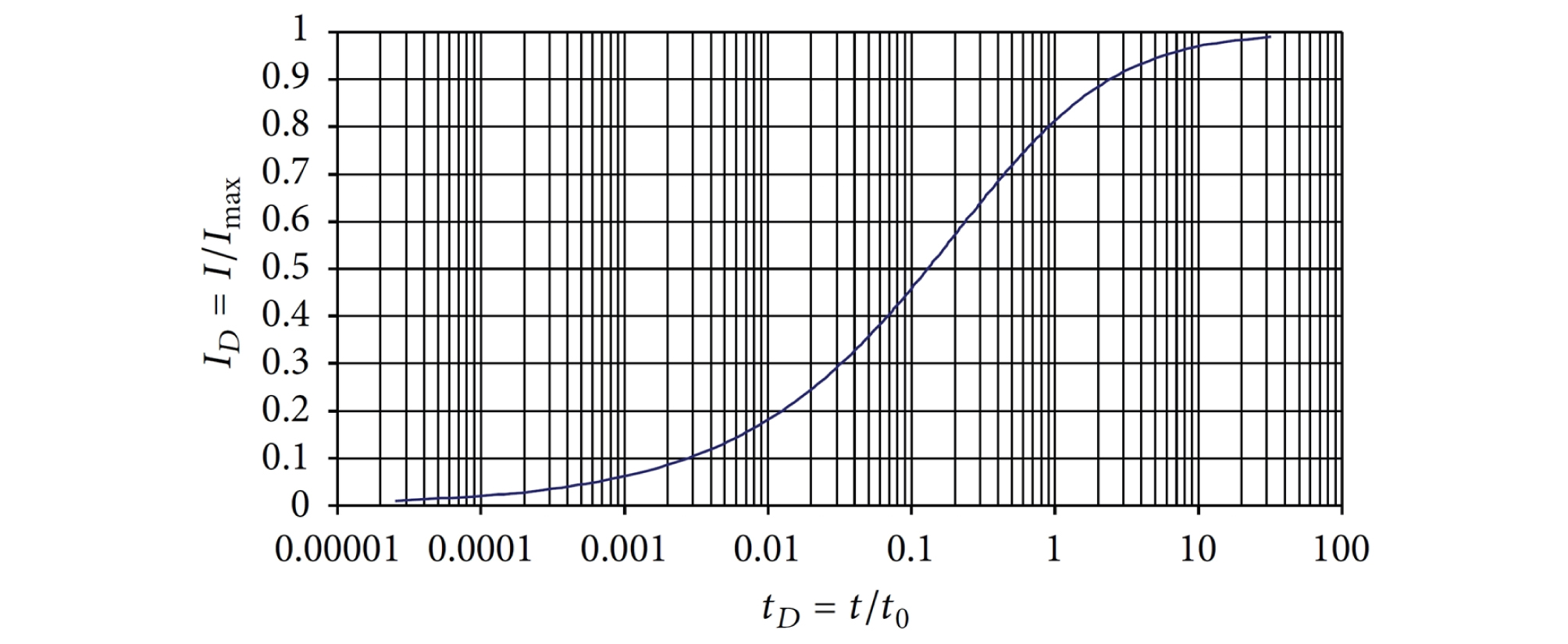
Fig. 5.
Relative penetration depth in the horizontal fracture as a function of relative penetration time (Gustafson et al., 2013)
4. 압축 벤토나이트 침투관련 물성
4.1 압축 벤토나이트 팽윤압
일반적으로 압축 벤토나이트의 팽윤압은 벤토나이트의 건조밀도가 증가함에 따라 증가하며, 팽윤압과 벤토나이트의 건조밀도 사이에는 지수적 증가 관계가 있다(Lloret et al., 2003; Komine, 2004). KJ-I 벤토나이트의 팽윤압은 건조밀도가 1.4 ~ 1.8 Mg/m3일 때, 0.647 MPa에서 14.07 MPa 사이의 값을 가지며, 벤토나이트 건조밀도가 증가함에 따라 급격히 증가한다(Cho et al., 2012). 20°C에서 측정된 건조밀도 1.4 ~ 1.8 Mg/m3인 KJ-I 벤토나이트의 팽윤압과 벤토나이트의 건조밀도 사이의 관계는 식 (30)으로 근사 될 수 있고, 건조밀도 1.6 Mg/m3인 KJ-I 벤토나이트의 팽윤압을 구하면 4.568 MPa이다.
| $$\sigma_s=1.541\times10^{-1}\;\exp\;(\frac{\rho_d}{1.586\times10^{-1}})\;+8.284\;\times\;10^2\;\;\;\;\;\;\;\;r^2=0.98$$ | (30) |
여기서, σs와 ρd는 각각 벤토나이트의 팽윤압(kPa)과 벤토나이트의 건조밀도(Mg/m3)이다. KJ-I 벤토나이트의 기타 물성은 참고문헌(Cho et al., 2012)에서 찾아볼 수 있다.
4.2 압축 벤토나이트 점도
일반적으로 유체 내에 고체 입자가 존재하면, 유체의 점도는 증가한다. 수중에 존재하는 고체 입자의 양이 작고, 입자가 구형이면, Einstein 관계식을 사용하여 겔(gel)의 점도를 추정할 수 있으나 (Bird, 2002; Hiemenz, 1986), 이 관계식은 벤토나이트의 함량이 아주 낮은 경우에만 적용될 수 있고, 압축 벤토나이트에는 사용할 수 없다. 벤토나이트 슬러리에서 슬러리 중의 벤토나이트 함량이 증가함에 따라 점도가 급격히 증가한다고 보고되었다(Asada and Horiuchi, 2005). 벤토나이트의 함량이 높아지면, 겔의 점도는 보통 물의 점도보다 수 차수(order) 이상 높아지며, 비 뉴턴 유체의 거동과 교반 또는 전단응력 하에서 시간이 경과함에 따라 점도가 감소되는 틱소트로피 특성(thixotropic property)을 보이기 시작한다. 또 벤토나이트 겔의 점도는 겔의 이온농도에도 크게 영향을 받는다(Moreno et al., 2010).
그러나 현재 보고된 벤토나이트 점도에 관한 데이터의 대부분은 벤토나이트 현탁액(suspension)에 관한 것이고, 압축 포화벤토나이트의 점도에 대한 정량적 데이터는 거의 없고, Pusch (1983)가 제안한 압축 포화벤토나이트의 점도 추정치가 유일한 실정이다 (Table 1). Table 1에서 볼 수 있는 바와 같이, 밀도가 1.2 Mg/m3 이하인 벤토나이트는 점도가 상당히 낮으나, 밀도가 1.5 Mg/m3 이상이 되면, 벤토나이트의 점도가 급격히 증가한다.
Table 1.
Estimated viscosity of saturated bentonite (Pusch, 1983)
| Density, ρm (Mg/m3) | Viscosity, μ (MPa・s) |
| 1.9 | 106 ~ 108 |
| 1.5 | 101 ~ 104 |
| 1.2 | 2 × 10-2 |
| 1.1 | ~ 10-4 |
4.3 압축 벤토나이트 항복강도
압축 벤토나이트의 항복강도는 벤토나이트의 건조밀도가 증가할수록 증가하며, 동일한 건조밀도에서는 수분흡입력(suction)이 감소할수록 감소한다. 건조밀도 1.78 Mg/m3인 MX-80 벤토나이트의 항복강도는 수분흡입력이 110 MPa인 경우에 17 MPa, 39 MPa인 경우에는 2.1 MPa이고, 수분흡입력이 9 MPa로 감소하면, 항복강도가 0.38 MPa로 급격히 떨어진다(Tang et al., 2008). 또 건조밀도 1.70 Mg/m3인 GMZ 벤토나이트의 항복강도도 수분흡입력이 110 MPa인 경우에 21 MPa, 39 MPa인 경우에 10 MPa이고, 수분흡입력이 9 MPa로 감소하면, 항복강도도 2 MPa로 감소하였다(Yui et al., 2011). FEBEX 벤토나이트에서도 유사한 경향이 보고되었다(Lloret et al., 2003). 온도가 상승하면, 압축 벤토나이트의 항복강도가 감소하여, 건조밀도가 1.70 Mg/m3, 수분흡입력이 110 MPa인 GMZ 벤토나이트의 항복강도는 온도 25°C일 때는 21 MPa이나 온도가 60°C로 증가하면 16 MPa로 감소하였다. 벤토나이트의 수분흡입력이 39 MPa인 경우에는, 온도가 25°C일 때는 항복강도가 10 MPa이나, 온도가 60°C로 증가하면 7.3 MPa가 된다(Tang et al., 2008), 건조밀도가 1.78 Mg/m3인 MX-80 벤토나이트의 항복강도에 미치는 온도의 영향도 비슷한 결과가 보고되었다.
처분공에 설치된 KJ-I 포화벤토나이트는 건조밀도가 1.6 Mg/m3으로 위에 기술한 MX-80 벤토나이트의 건조밀도인 1.78 Mg/m3보다 작고, 지하수로 완전히 포화되었기 때문에 수분흡입력이 9 MPa보다 낮을 것이 확실하므로, 항복강도가 위에서 기술한 건조밀도 1.78 Mg/m3, 수분흡입력 9 MPa인 MX-80 벤토나이트의 항복강도 값보다 작을 것이다. 또 사용후핵연료에서 발생되는 방사성붕괴열로 인해, 처분공에 존재하는 압축 벤토나이트 완충재의 온도는 60°C 이상으로 상승될 것이므로, 항복강도 값이 더욱 감소할 것으로 예상된다. 따라서 처분공에 존재하는 건조밀도 1.6 Mg/m3인 KJ-I 포화벤토나이트 완충재의 항복강도는 0.5 MPa보다 작을 것이라고 보는 것이 타당하다.
5. 압축 벤토나이트 침투 평가
5.1 입력인자
Bingham 유체 모델을 이용해서 처분공 내벽에 형성된 손상영역 암반 불연속면 내로 압축 벤토나이트 완충재가 침투하는 현상을 모사하기 위해서는 입력인자로 포화 압축 벤토나이트의 팽윤압, 항복강도, 점도 및 불연속면의 폭의 값이 필요하다. 모델에 필요한 각 입력인자들의 값은 앞절에 기술된 벤토나이트 물성에 관한 연구결과들을 고려하여, 적절한 값을 택하였다. 포화 압축 벤토나이트의 팽윤압은 식 (30)을 이용하여 추정한 건조밀도가 1.6 Mg/m3인 KJ-I 벤토나이트의 팽윤압인 4.536 MPa을 사용하였으며, 항복응력은 벤토나이트가 포화조건인 것을 고려하여, 0.1, 0.3 및 0.5 MPa의 세 가지 값을 고려하였다. 포화 압축 벤토나이트의 점도는 1.0 × 103 MPa·s, 5.0 × 105 MPa·s 및 1.0 × 106 MPa·s의 세 가지 값에 대해 분석하였다. 손상영역 암반 불연속면의 폭은 0.1 mm, 0.5 mm 및 1.0 mm의 세 종류를 고려하였다. 손상영역 암반 불연속면 내로 압축 벤토나이트 완충재가 침투하는 현상의 모사에 사용된 입력인자의 값들을 Table 2에 정리하였다.
Table 2.
Value of parameters used in the modelling of KJ-I bentonite penetration into rock fracture
| Parameters | Value | ||
| Swelling Pressure (MPa) | 4.536 | ||
| Yield Strength (MPa) | 0.1 | 0.3 | 0.5 |
| Aperture (mm) | 0.1 | 0.5 | 1.0 |
| Viscosity (MPa・s) | 1.0×105 | 5.0×105 | 1.0×106 |
5.2 최대 침투깊이
처분공 내벽에 형성된 손상영역 암반 불연속면 내로 벤토나이트 완충재가 침투할 수 있는 최대 깊이는 식 (9)에 의해 계산할 수 있다. 계산에 사용된 압축벤토나이트의 팽윤압 값은 4.536 MPa이다. 벤토나이트의 최대 침투깊이는 포화 압축벤토나이트의 팽윤압과 암반 불연속면의 폭에 비례하고, 압축벤토나이트의 항복강도에 반비례한다. 최대 침투깊이는 압축벤토나이트의 항복응력이 0.5 MPa, 암반단열의 폭이 0.1 mm 일 때 최소치인 0.4 mm를 나타내고, 압축벤토나이트의 항복응력이 0.1 MPa, 암반단열의 폭이 1.0 mm인 경우에 최대치인 22.6 mm를 나타내는 등, 입력인자들의 값에 따라 다양한 최대 침투깊이를 나타내었다. 암반단열 폭과 포화 압축벤토나이트 항복응력의 변화에 따른 건조밀도 1.6 Mg/m3인 KJ-I 벤토나이트의 최대 침투깊이를 Table 3에 수록하였다.
Table 3.
Maximum penetration of KJ-1 bentonite into rock farcture
5.3 시간 경과에 따른 벤토나이트의 침투
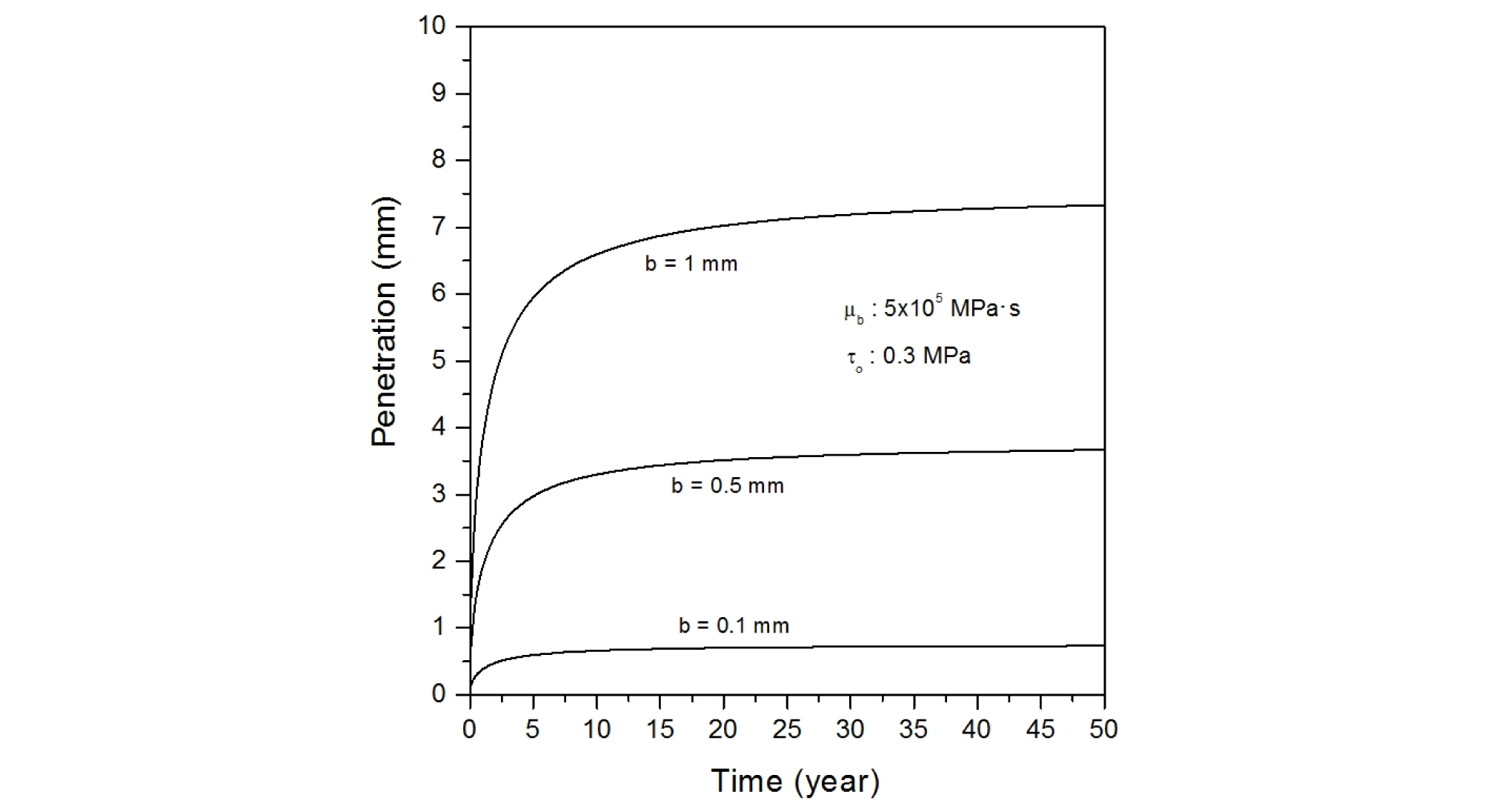
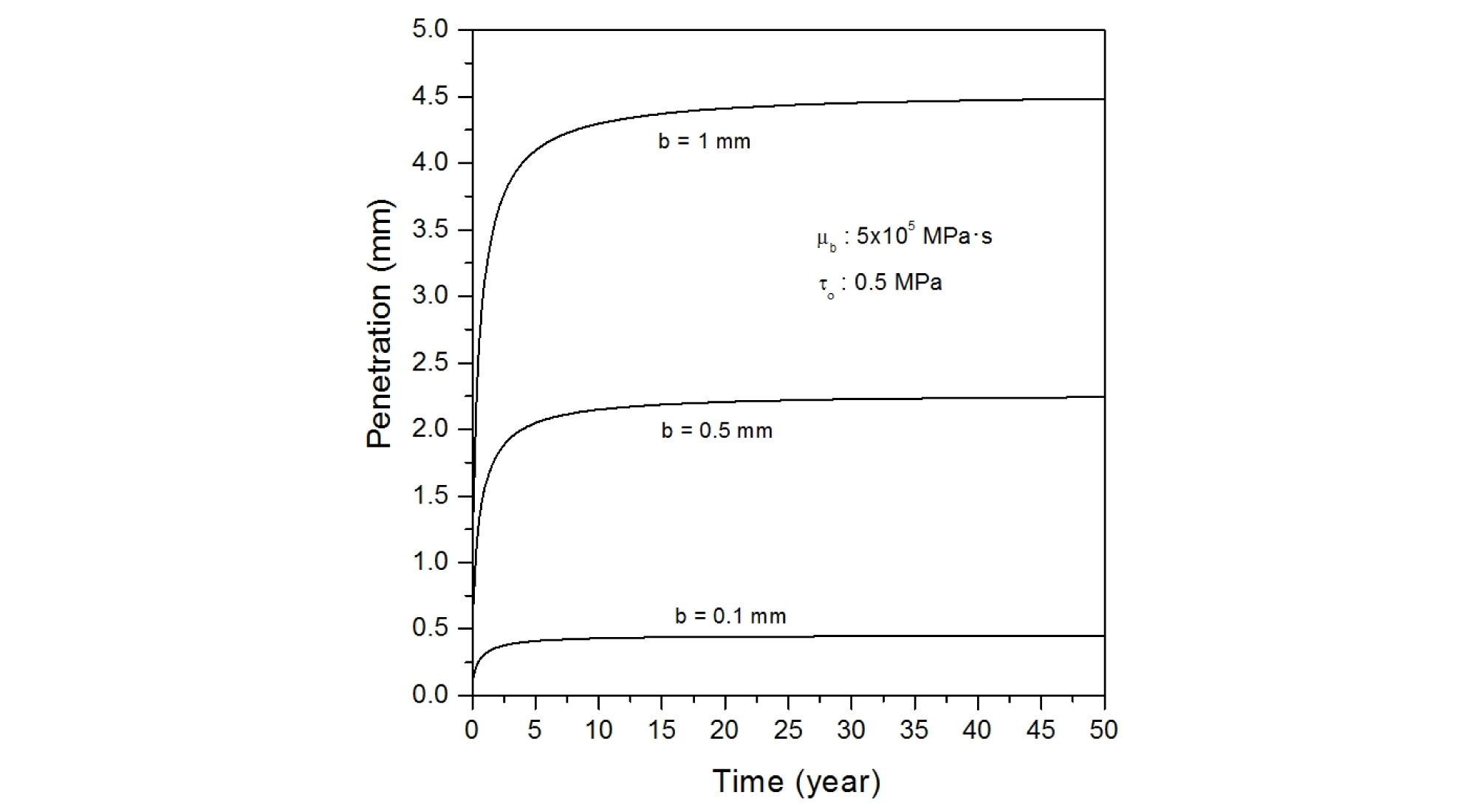
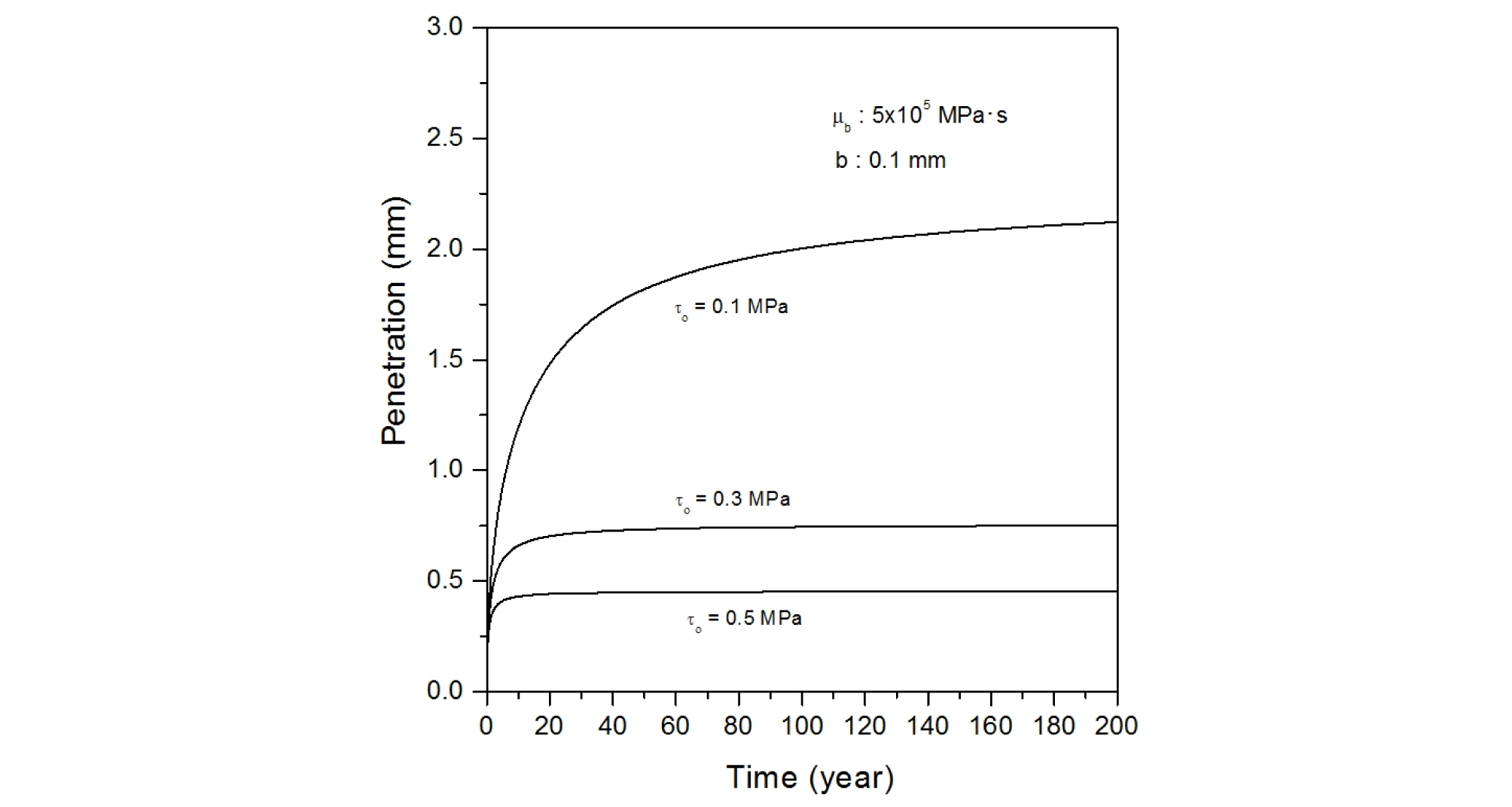
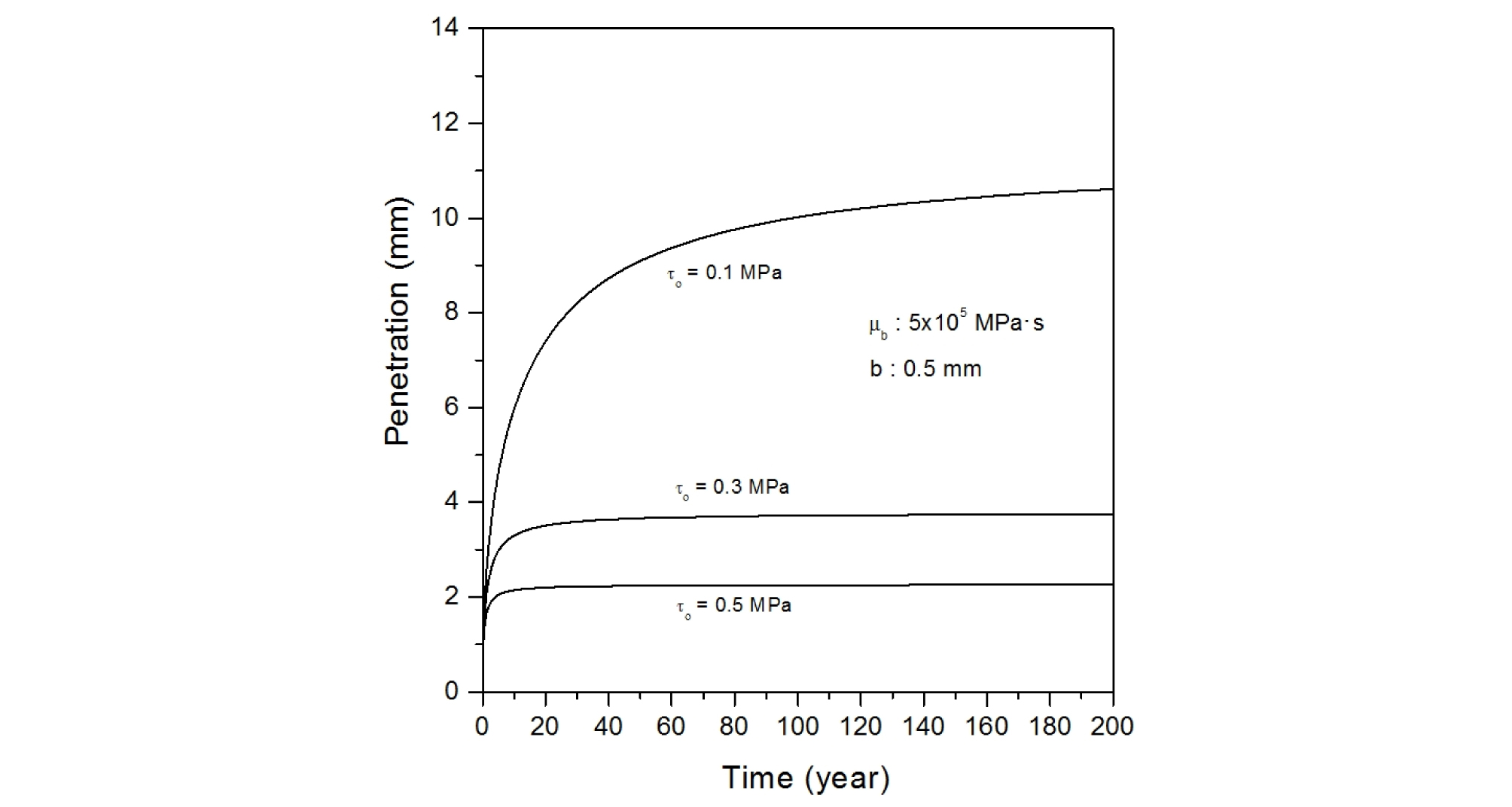
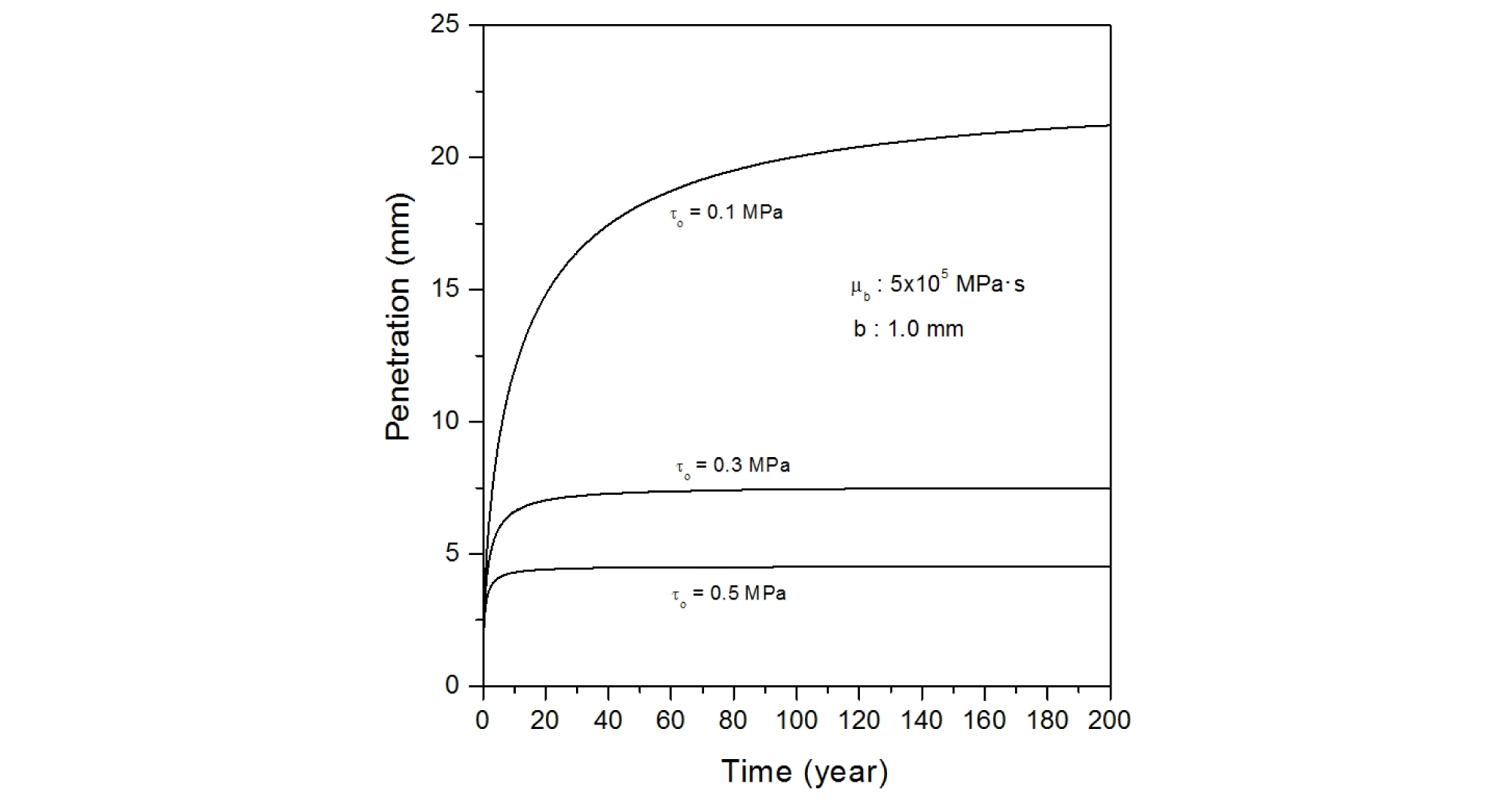
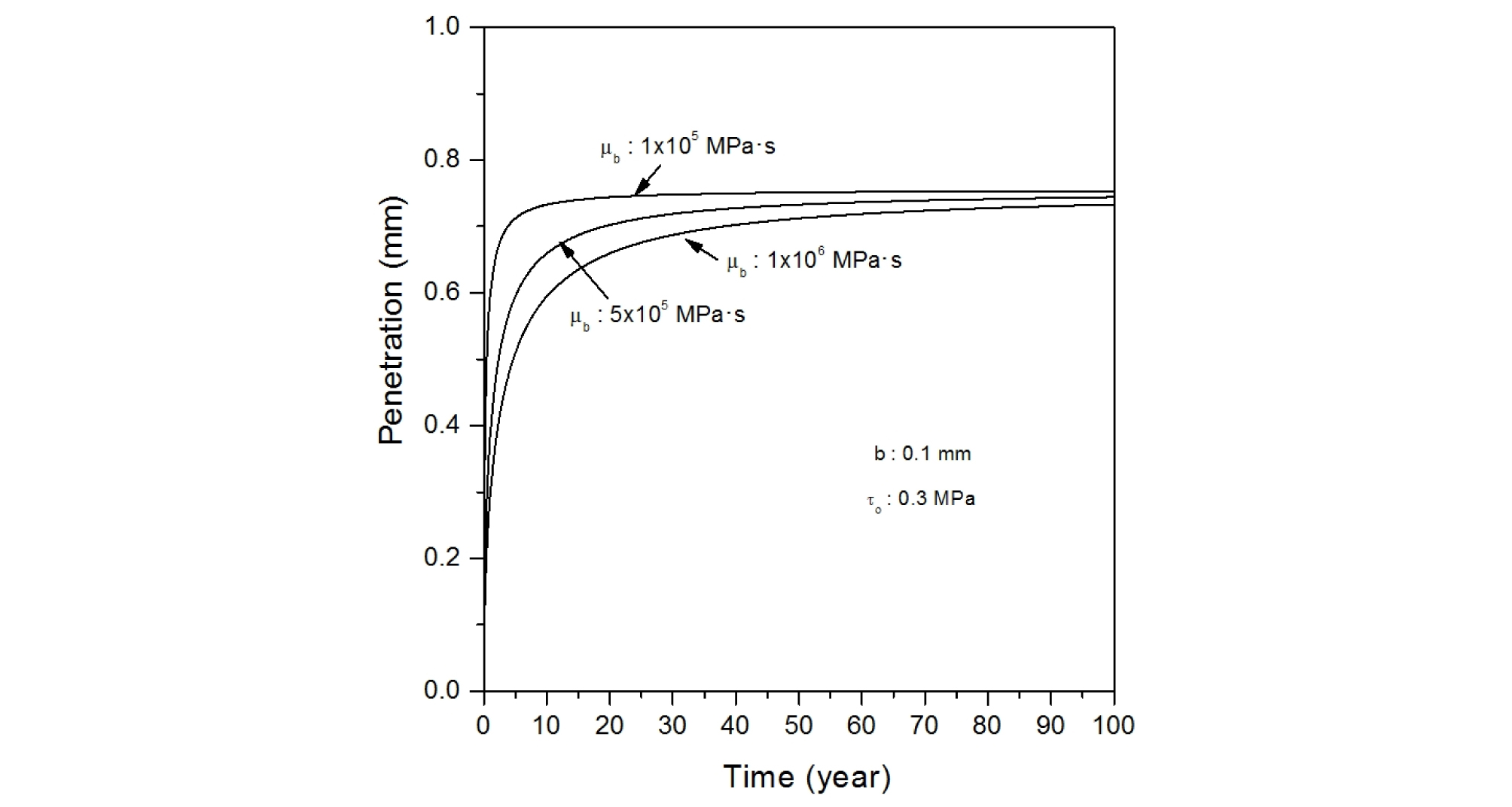
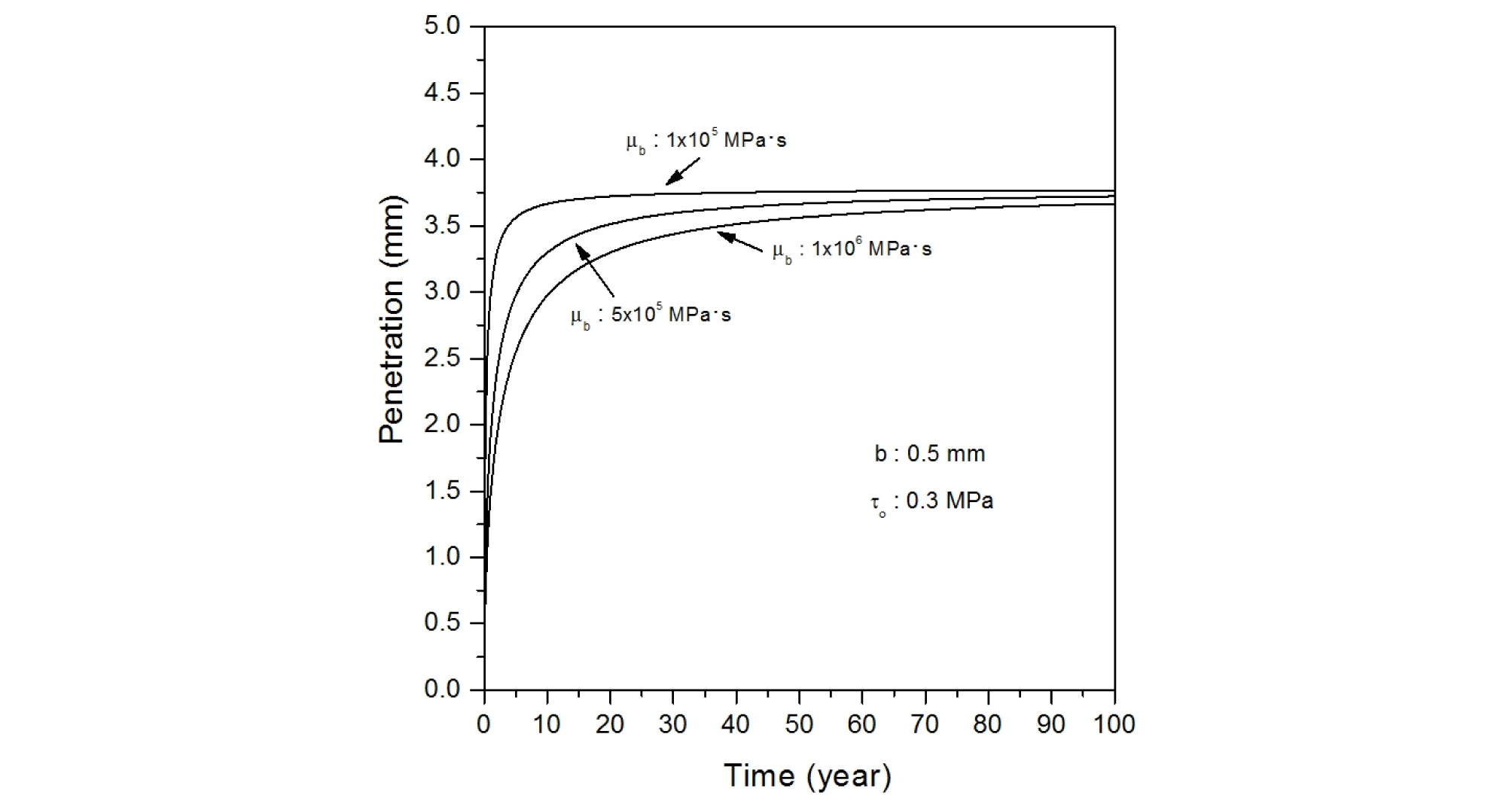
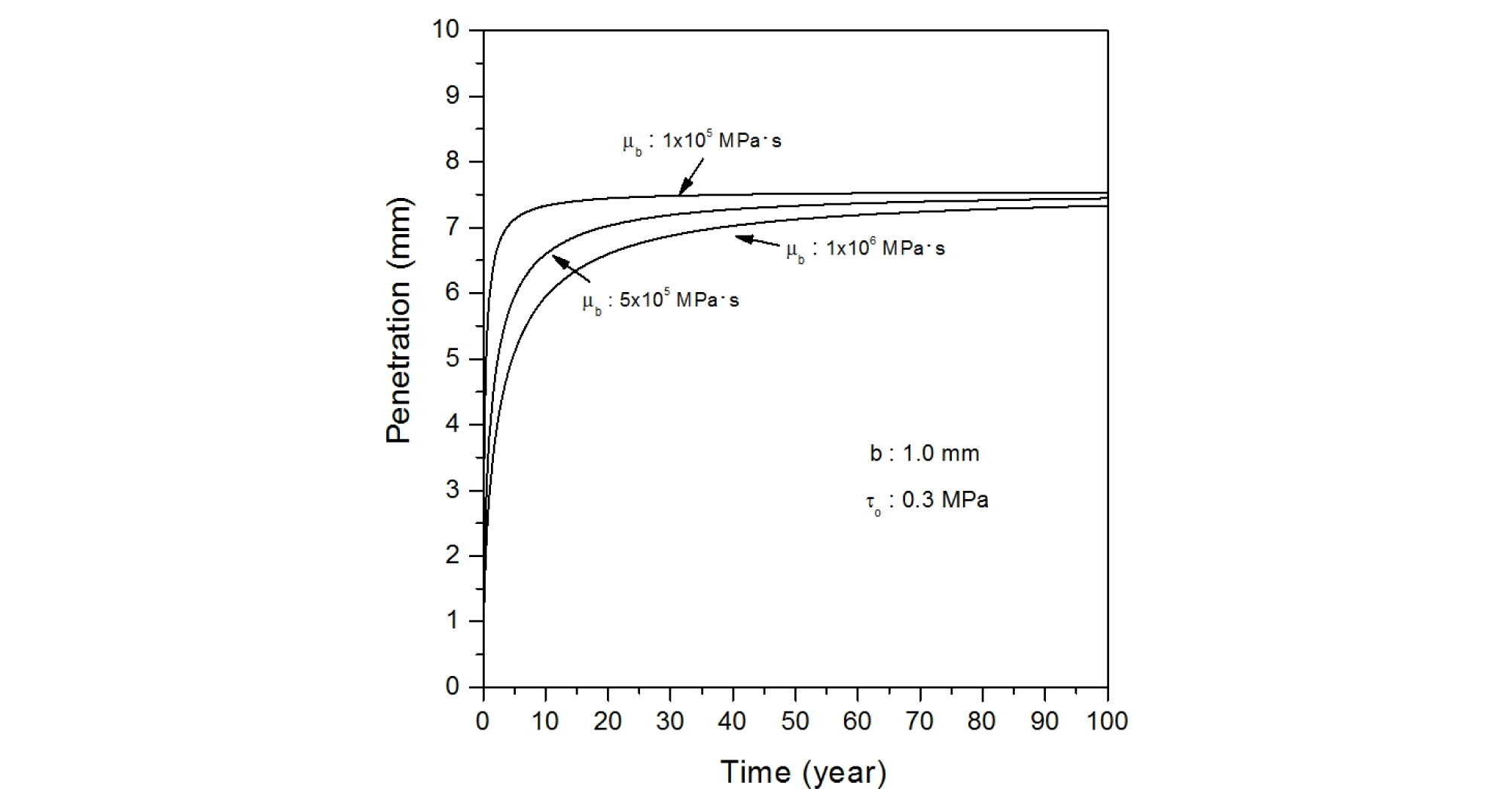
Table 2에 나타나 있는 각 세 종류의 포화벤토나이트 항복응력, 포화벤토나이트 점도 및 불연속면의 폭을 조합한 총 27 가지 경우에 대해, 시간 경과에 따른 압축 벤토나이트의 침투깊이를 계산하였으며, 주요 결과를 정리하여 Fig. 6에서 Fig. 14에 나타내었다.
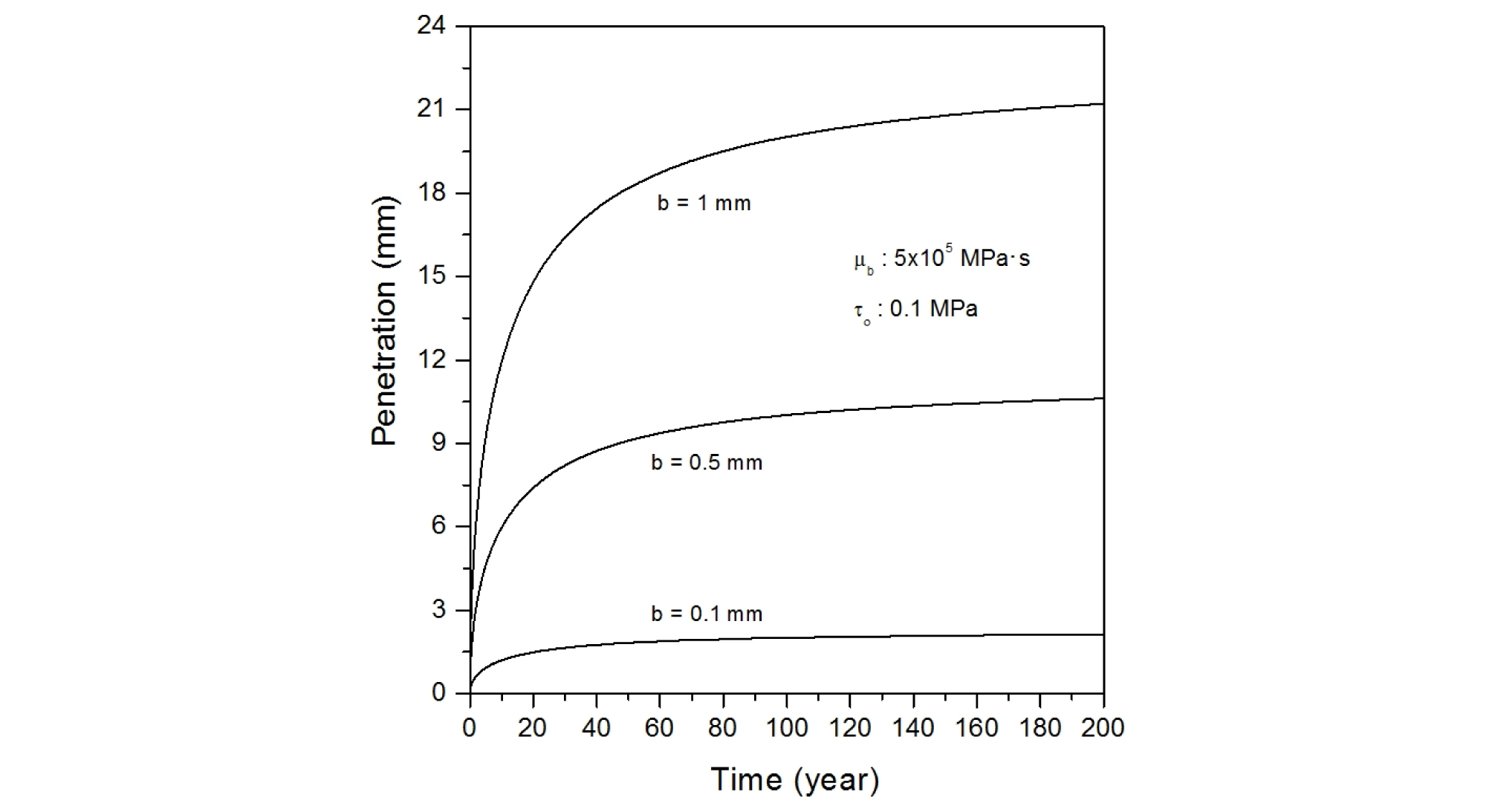
포화 벤토나이트의 점도가 5.0 × 105 MPa·s이고 압축 벤토나이트의 항복강도가 0.1, 0.3 및 0.5 MPa일 때, 여러 암반 불연속면의 폭에서 시간에 따른 벤토나이트 침투깊이를 Fig. 6에서 Fig. 8에 나타내었다. 동일한 항복응력 하에서는 암반 불연속면의 폭이 증가할수록 벤토나이트의 침투깊이가 커지며, 최대 침투깊이에 도달하는데 걸리는 시간도 증가한다. 벤토나이트의 항복강도가 0.1 MPa이고, 암반 불연속면의 폭이 1.0 mm일 때는 약 200년이 경과하여도 최대 침투깊이에 도달하지 못하나, 암반 불연속면의 폭이 0.1 mm인 경우에는 수십 년만 경과하면, 거의 최대 침투깊이까지 도달하는 것으로 나타났다. 이는 암반 불연속면의 폭이 작을수록 불연속면에 작용하는 포화 압축 벤토나이트의 팽윤압이 작기 때문이다. 그러나 압축 벤토나이트의 항복강도가 증가하면, 최대 침투깊이에 도달하는 시간이 감소하여, 항복강도가 0.5 MPa이고, 불연속면의 폭이 0.1 mm인 경우에는 수년 내에, 불연속면의 폭이 1.0 mm인 경우에는 수십 년 정도 경과하면, 압축 벤토나이트가 거의 최대 침투깊이에 도달한다. 이는 압축 벤토나이트의 항복강도가 증가하면 암반 불연속면 내로 침투하는 벤토나이트에 대한 저항력이 커지므로, 벤토나이트가 짧은 시간에 단거리만 침투한 후 정지되기 때문이다.
포화 압축 벤토나이트의 점도가 5 × 105 MPa·s이고 암반 불연속면의 폭이 0.1 mm, 0.5 mm 및 1.0 mm일 때, 다양한 압축 벤토나이트의 항복강도에 대해 시간에 따른 벤토나이트 침투깊이 변화를 Fig. 9에서 Fig. 11에 나타내었다. 동일한 암반 불연속면의 폭에서는 압축 벤토나이트의 항복강도가 증가할수록 침투깊이가 감소하며, 최대 침투깊이에 도달하는데 걸리는 시간도 짧아진다. 암반 불연속면의 폭이 0.1 mm일 때, 압축 벤토나이트의 항복강도가 0.1 MPa인 경우에는 약 200년이 경과하여도 최대 침투깊이에 도달하지 못하나 압축 벤토나이트의 항복강도가 0.5 MPa인 경우에는 수년 정도 경과하면, 거의 최대 침투깊이까지 도달한다. 암반 불연속면의 폭이 커지면, 압축 벤토나이트의 최대 침투깊이가 증가하나, 압축 벤토나이트의 항복강도 변화 시, 시간에 따른 침투깊이 변화 경향은 거의 유사하다. 이것은 앞에서 언급한 바와 같이. 압축 벤토나이트의 항복강도가 증가하면 암반 불연속면 내로 침투하는 벤토나이트에 대한 저항력이 증가하기 때문이다.
압축 벤토나이트의 항복강도와 암반 불연속면의 폭이 일정할 때, 포화벤토나이트의 점도 변화가 암반 불연속면 내로의 벤토나이트 침투에 미치는 영향을 Fig. 12에서 Fig. 14에 나타내었다. 동일한 암반 불연속면의 폭과 압축 벤토나이트의 항복강도에서, 압축 벤토나이트의 점도가 낮을 때에는 침투속도가 빨라 수년 정도의 단기간에 최대 침투깊이에 도달하나, 점도가 증가할수록 최대 침투깊이에 도달하는 시간이 증가한다. 압축 벤토나이트의 항복강도가 0.3 MPa이고, 암반 불연속면의 폭이 0.1 mm인 경우에는 약 100년이 경과하여야 벤토나이트가 최대 침투깊이까지 접근하게 된다. 암반 불연속면의 폭이 증가하면, 최대 침투깊이가 증가하지만, 압축 벤토나이트의 점도 변화에 따른 침투속도 변화 경향은 유사하다.
6. 결 론
심층처분장 처분공에 설치된 압축 벤토나이트 완충재가 처분공 내벽에 형성된 손상영역의 불연속면 내로 침투하는 현상을 모사하기 위한 수학적 모델을 개발하였다. 암반 불연속면 내로 벤토나이트가 침투하는 현상을 모사하기 위해 제안된 기존 모델을 조사하여, 그 특성과 한계점을 분석하였다. 암반 불연속면 내로의 벤토나이트 침투 메카니즘을 바탕으로 암반 불연속면과 압축 벤토나이트 완충재 특성의 함수로서 압축 벤토나이트가 암반 불연속면 내로 침투하는 거리와 침투속도를 추정할 수 있는 정량적 모델을 제시하였다.
처분공 내벽에 형성된 손상영역 내로의 압축 벤토나이트 침투현상은 평행평판 암반균열을 통한 Bingham 유체의 이동으로 모사될 수 있다. 암반 불연속면을 통해 압축 벤토나이트가 침투하는 최대 깊이는 포화 압축 벤토나이트의 팽윤압과 암반 불연속면의 폭에 비례하며, 압축 벤토나이트의 항복강도에 반비례한다. 압축 벤토나이트의 점도는 압축 벤토나이트의 침투 속도를 좌우하나, 최대 침투깊이에는 영향을 미치지 않는 것으로 나타났다.
이 연구를 통해 제시된 완충재 침투모델의 유용성을 확인하기 위해서는 손상영역의 불연속면 내로 압축 벤토나이트 완충재가 침투하는 현상에 대한 실험적 규명이 필요하다. 이를 위해 먼저 점도 및 항복강도 등 침투현상을 좌우하는 압축 벤토나이트의 특성을 실험적으로 측정한 후, 실내에서 암반 불연속면을 통한 압축 벤토나이트 완충재의 침투 실험을 실시하여 실험에서 얻은 결과와 제안된 모델에 의해 계산한 결과를 비교하는 작업이 수행되어야 한다. 궁극적으로는 지하연구시설에 존재하는 암반 불연속면을 이용하여 압축 벤토나이트 완충재가 손상영역 암반 불연속면 내로 침투하는 현상을 규명하기 위한 현장실험을 수행할 필요가 있다. 또 손상영역 암반 불연속면 내로 압축 벤토나이트 완충재의 침투는 처분공 주위 근계암반의 열전도도를 증가시키고, 수리전도도와 역학적 건전성을 저하시며 완충재와 근계암반의 열-수리-역학적 거동에 영향을 미칠 수 있다. 이러한 열-수리-역학적 거동에 대한 영향은 심층처분시스템의 건전성을 저하시킬 수 있는 중요한 요소이므로, 이에 대한 평가가 상세한 분석과 평가가 필요하다.
이와 같은 추가 연구를 통해 심층처분장의 성능에 불확실성을 초래할 수 있는 인자의 영향을 사전에 확인하고, 이를 설계에 반영하는 과정을 통해 사용후핵연료 심층처분의 신뢰도를 향상시키는 것이 중요하다.