1. 서 론
2. 배경이론
2.1 직경분포 추정식의 유도
2.2 기존 Joint Center Volume (JCV) 산정 기법
3. 새로운 Joint Center Volume (JCV) 산정 기법 제안
3.1 비평면 조사창에서의 절리선 종류
3.2 몬테카를로 시뮬레이션을 이용한 Joint Center Volume (JCV) 산정 기법
4. 적용성 검토
4.1 곡면 조사창 추정결과
4.2 터널형 조사창 추정결과
4.3 추정결과에 대한 논의
5. 결 론
1. 서 론
터널, 사면, 광산갱도 등과 같은 암반구조물에서 암반절리는 안정성과 관련된 매우 중요한 요소이다. 암반 내에 존재하는 절리는 직접적으로 구조물의 역학적 안정성을 저하시킬 수 있을 뿐 아니라, 지하수 유입에 따른 부가적인 문제를 발생시킬 수 있다. 따라서 암반공학분야의 다양한 실험적, 수치해석적 연구에서 정확한 암반절리 파라미터의 사용이 필수적으로 요구되고 있다 (Um and Han, 2017).
암반절리 파라미터는 방향, 간극, 형상, 크기, 거칠기 등이 있으며, 대부분의 파라미터는 노출면 또는 시추공에서의 실측결과를 기반으로 확률분포 형태로 분석된다 (ISRM, 1978). 그러나 암반 내에 존재하고 있는 절리의 형상과 크기는 일반적으로 절리가 암반 내부에 존재하고 있으며, 암반 자체가 빛과 전자기파에 대해 불투과성을 보이므로 직접적인 측정이 불가능하다 (Priest, 1993).
이와 관련하여 대부분의 연구에서는 계산상의 편의를 위해 원판형 절리가 3차원 공간상에 무작위로 위치한다고 가정하는 포아송 디스크 모델 (Baecher et al., 1997)을 적용하고 있다. 이 모델의 장점은 절리의 크기를 원판의 직경으로 간단하게 나타낼 수 있다는 것이다. 퇴적층리 암반에 대해서는 절리형상을 사변형으로 정의하는 경우도 있다 (Pollard and Aydin, 1988).
절리의 크기(직경)분포는 측정 가능한 절리선(joint trace) 조사결과를 이용한 추정기법이 연구되어 오고 있으며, 크게 귀납적 방법과 연역적 방법으로 나누어 볼 수 있다. 귀납적 방법은 분포종속적(distribution-dependent)인 방법으로, 처음부터 분포의 종류와 매개변수를 미리 가정하여 표본분포를 도출한 다음 실제로 조사된 표본분포와 비교하여 오차율에 따라 분포를 추정하게 된다 (La Pointe et al., 1993). 연역적 방법은 분포독립적(distribution-free)인 방법이며, 분포를 미리 가정하지 않고 현장에서 조사된 절리선 길이분포를 이용하여 직접적으로 추정하게 된다. 귀납적 방법과 연역적 방법은 서로 해석의 순서가 반대이지만 모두 절리선 길이분포가 절리 직경분포의 적분함수로 표현되는 이론식을 사용한다 (Song, 2005).
Warburton(1980)이 직경분포와 절리선 길이 누적분포와의 관계식을 밝힌 이래로 귀납법, 연역법을 이용한 다양한 연구들이 수행되어 오고 있으며, 최근에는 주로 무한크기 조사창에서의 절리선 길이분포(true trace length distribution)을 이용한 추정법들이 제안되고 있다 (Hehua et al., 2014; Amin et al., 2018). 그러나 이러한 연구들은 평면 조사창에서의 절리선 길이분포와 체적빈도를 이용하여 추정하기 때문에 충분한 크기의 조사창을 설치할 수 있어야 한다. 조사창 평면의 크기가 작을수록 신뢰도는 감소할 수밖에 없으며, 이는 현장상황에 따라 추정 정확도에 차이를 보임을 의미한다.
Jeon et al.(2011)과 Suh and Song(2016)은 이러한 평면 조사창 기법들의 단점을 극복하고자 조사창의 형상을 원통형으로 확장하여 분석한 바 있다. 분석과정에서 Joint Center Volume (JCV)의 개념을 사용하였으며, 이는 Song(2009)이 정립한 개념으로 조사창 내에 특정 길이를 가지는 절리선이 존재하기 위해 암반 내에서 절리의 중심이 위치해야 하는 지점의 공간적 크기를 의미한다. Song(2009)은 이러한 JCV를 이용한 절리 직경분포 추정이 상당한 신뢰성을 보임을 검증하였으며, 이 과정에서 평면 조사창 내 절리선을 양끝내포선(contained trace), 한끝내포선(dissecting trace), 양끝외포선(transecting trace)로 구분하고, 각각의 JCV를 이론적으로 산정하는 방법을 제시하였다.
본 연구에서는 이러한 선행연구들에서의 JCV 산정 기법들에 대해 조사하여 한계점을 분석하였으며, 이를 보완한 새로운 JCV 산정 기법을 제안하였다. 제안된 기법은 조사창 형상과 관계없이 평면, 비평면에서 모두 활용될 수 있으며, 몬테카를로 시뮬레이션을 이용한 검증 결과 다양한 분포에서 적용이 가능하다고 판단되었다.
2. 배경이론
Joint Center Volume(JCV)는 절리선 길이분포와 절리 직경분포의 적분식을 이산화하여 분석할 시 유용하게 활용된다. 여기서는 JCV를 이용하여 직경분포를 추정하는 과정에 대해 설명하고, JCV를 이용한 선행연구들에 대해 분석하였다.
JCV를 이용한 선행연구는 Song(2005), Song(2009), Jeon et al.(2011), Suh and Song(2016)이 있으며, 이를 이용한 직경분포 추정은 대부분 초기 정립된 Song(2005)의 유도 방법을 따르고 있다.
2.1 직경분포 추정식의 유도
본 연구에서는 모든 절리선 종류를 활용하여 절리 직경분포를 추정한 Song(2009)의 알고리즘을 기반으로 JCV를 추정하고자 하였다. 그 밖의 JCV를 이용한 선행연구들은 모두 양끝내포선(contained trace)만을 이용해 절리 직경분포를 추정하였고, 오차율이 비교적 높게 나타났다.
계산상의 편의를 위해 절리는 포아송 디스크 모델을 따른다고 가정한다. 이는 절리가 두께가 없는 원판형이며, 3차원 공간 상에 무작위로 위치한다고 보는 것이다. 또한 특정 절리군에 속한 절리들은 모두 동일한 방향성을 가져 평행함을 가정한다. 이 가정 하에서 절리 직경분포의 추정은 절리군 별로 이루어진다.
여기서 필요한 개념이 JCV이며, 기본적으로 JCV(l,s)와 같이 표현된다. JCV(l,s)는 직경이 s인 절리가 조사창과 만나서 길이 l의 절리선을 나타내기 위해서 절리 중심점이 위치 가능한 공간 상 부피를 의미한다. 이와 함께 단위부피의 암반 내 존재하는 절리의 개수를 의미하는 체적빈도(λv)가 주어지면, 다음 식 (1)과 같이 직경 s인 절리로 인해 조사창 내에서 조사되는 길이 l인 절리선의 개수(N(l,s))를 구할 수 있다.
| $$N_{(l,s)}=JCV_{(l,s)}\times\lambda_\nu$$ | (1) |
그러나 암반 내에 존재하는 절리의 직경은 분포형태로 다양하게 존재하기 때문에 위 식을 통해 직접적으로 구할 수 없으며, 절리 직경의 확률밀도함수(cs)를 적용하여 계산해야 한다. 위 식 (1)은 모든 절리가 직경 s인 경우로 한정된다.
따라서 확률밀도함수를 적용한 다음 식 (1)을 모든 절리 직경에 대해 적분을 하게 되면 최종적으로 식 (2)와 같이 조사창 내 길이 l인 절리선의 개수(Nl)를 구할 수 있다. 직경분포를 이산함수로 가정하면 식 (2)는 식 (3)과 같이 표현할 수 있으며, 여기서 i는 절리선 계급, j는 절리 직경의 계급, n은 절리 직경의 계급구간의 개수를 의미한다. 식 (3)에서 cj를 제외한 항들을 묶으면 식 (4)과 같은 형태로 정리가 가능하다.
| $$N_l=\int_{S_{min}}^{S_{max}}(JCV_{(l,s)}\times\lambda_\nu\times c_s)ds$$ | (2) |
| $$N_i=\sum_{j=1}^n(JCV_{ij}\times\lambda_\nu\times c_j)\triangle s$$ | (3) |
| $$N_i=\sum_{j=1}^n\alpha_{ij}c_j$$ | (4) |
식 (4)는 이론상 계산되는 i번째 계급의 절리선 개수를 의미하며, 절리의 직경분포를 의미하는 확률밀도함수 cj를 구하기 위해서 아래와 같이 현장에서 조사된 실측 절리선 개수(Ni΄)와 이론값의 오차제곱합을 이용한다. 여기서 m은 절리선 계급구간의 개수를 의미한다.
| $$E^2=\sum_{i=1}^m\left[N_I^`-N_I\right]^2=\sum_{i=1}^m\left[N_i^`-\sum_{j=i}^n\alpha_{ij}c_j\right]^2$$ | (5) |
상기 오차제곱합이 최소가 되는 경우의 직경분포(cj)를 구하기 위해 아래와 같이 ck에 대해 편미분한다.
| $$\frac{\partial E^2}{\partial c_k}=-2\sum_{i=1}^m\left[\left(N_i^`-\sum_{j=1}^n\alpha_{ij}c_j\right)\alpha_{ik}\right]=0\;,\;(1\leq k\leq n)$$ | (6) |
식 (6)은 식 (7)과 같이 정리될 수 있으며, 최종적으로 식 (8)과 같은 행렬식의 표현으로 간단하게 정리할 수 있다.
| $$\sum_{i=1}^mN_i^`\alpha_{ik}=\sum_{i=1}^m\sum_{j=1}^n\alpha_{ik}\alpha_{ij}c_j\;,\;(1\leq k\leq n)$$ | (7) |
| $$\lbrack A_{kj}\rbrack\;\lbrack c_j\rbrack=\lbrack b_k\rbrack$$ | (8) |
여기서,
결국 JCV가 산정되면, 현장에서 조사된 실측 절리선 개수(Ni΄)와 종합하여 식 (8)에서 절리 직경분포를 의미하는 cj를 제외한 모든 항이 구해진다. 따라서 식 (8)을 가우스 소거법(Gauss elimination), SOR법(successive over relaxation method), SUR법(successive under relaxation method), 경사하강법(Conjugate gradient method) 등 다양한 수치계산으로 풀어서 직경분포 cj를 구할 수 있다. 상기 식에서 aik, aij는 체적빈도 λv를 포함하고 있는데, 체적빈도는 직접적인 측정이 불가능하기 때문에 현장에서 도출하기 어려운 파라미터이다. 그러나 위 과정에서 λv를 1로 가정하고 직경분포를 구하게 되면, cj의 정규화 과정에서 분포의 면적이 절리의 체적빈도가 된다. 이는 계산 과정에서 λv의 상쇄를 통해 수치계산 시 λv·cj가 해로써 도출되며, 확률밀도함수의 정의상 cj의 면적은 1로 정규화되어야 하기 때문이다.
이 방법은 절리선 종류와 상관없이 적용될 수 있으며, 선행연구에서는 양끝내포선의 경우에 많이 적용되었다. Song(2009)은 이에 대해 양끝내포선, 한끝내포선, 양끝외포선을 모두 고려하여 추정 직경분포의 신뢰도를 높이고자 하였으며, 식 (5)의 관계식을 식 (9)와 같이 각각의 절리선 종류별로 나누어 오차제곱합을 최소화할 수 있도록 확장하였다. 여기서 첨자 c는 양끝내포선(contained trace), d는 한끝내포선(dissecting trace), t는 양끝외포선(transecting trace)를 의미한다. wi는 절리선 종류별 가중치벡터로 시행착오법(trial and error method)을 통해 오차제곱합이 최소가 되는 값으로 설정한다.
| $$E^2=\sum_{i=1}^m\left[\omega_i^c(N_I^{C^`}-N_I^C)^2+\omega_i^d(N_I^{d^`}-N_I^d)^2+\omega_i^t(N_I^{t^`}-N_I^t)^2\right]$$ | (9) |
그 이후에는 식 (6)~(8) 까지의 관계식이 그대로 적용되나, 절리선 개수의 이론값 계산 과정에서 JCV가 각 절리선 종류별로 다르게 적용되어야 한다.
2.2 기존 Joint Center Volume (JCV) 산정 기법
2.2.1 이론적 산정법
Song(2009)은 평면조사창에서 양끝내포선, 한끝내포선, 양끝외포선의 JCV를 구하기 위한 이론적 산정법을 제시하였다.
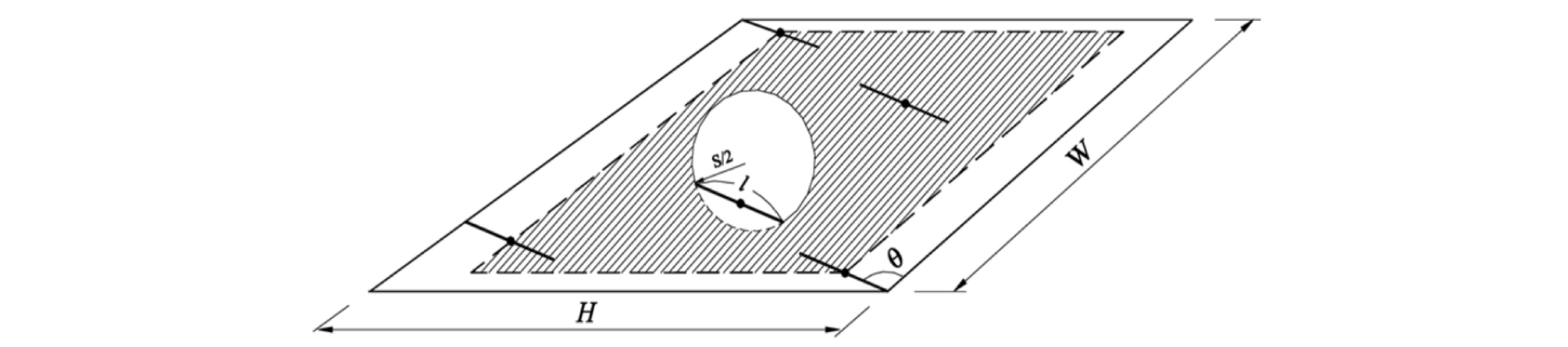
먼저 Fig. 1은 직경 s인 절리에 의해 길이 l을 가지는 양끝내포선이 생길 때, 이 중심이 W×H 크기의 직사각형 평면조사창 내에서 위치 가능한 영역을 빗금으로 표시한 것이다.
Fig. 1에서 빗금친 영역의 넓이는 아래와 같이 계산된다. 여기서 Lx΄은 조사창 내 최대 절리선 길이를 의미한다.
| $$A_l^c=(W-l\cos\theta)(H-l\sin\theta)\;,\;l<L_x^`$$ | (10) |
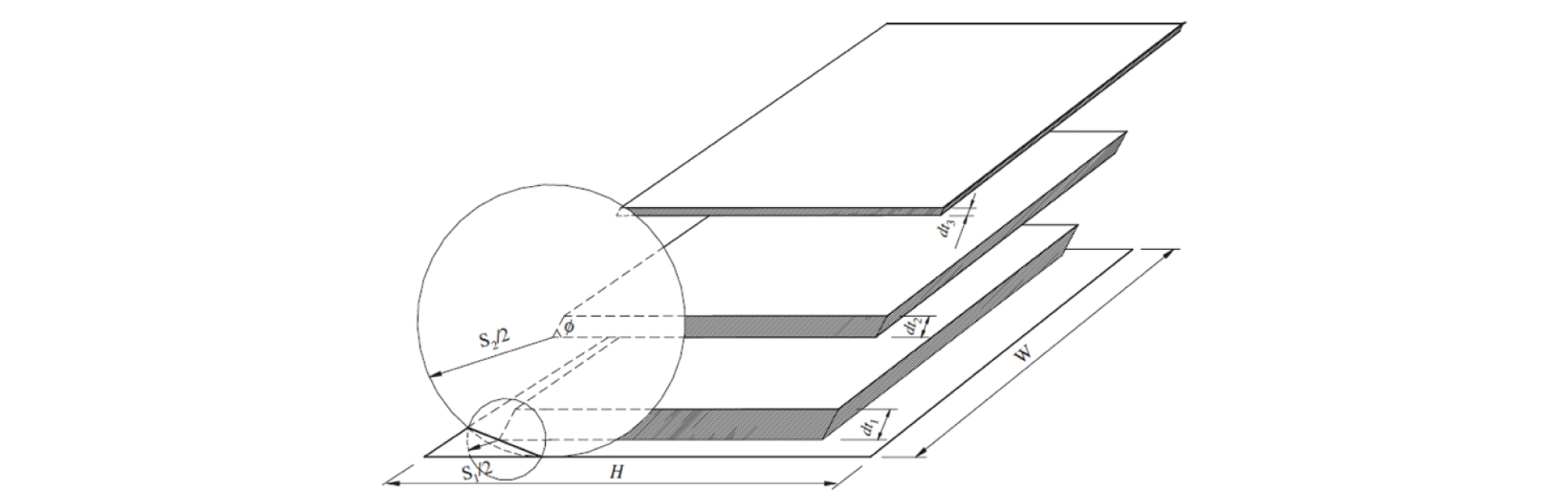
Fig. 2.
Variation of the parallelepiped volume of disc center according to the change in joint diameter for a constant trace length (Song, 2005)
양끝내포선의 JCV는 Fig. 2에서와 같이 평행육면체형으로 나타나며, 면적과 높이의 곱으로 계산할 수 있다. 이 때의 평행육면체의 높이(dt)는 양끝내포선 길이가 l-dl에서 l 사이의 길이를 가질 때 다음과 같다.
| $$dt=\frac{\sqrt{s^2-(l-dl)^2}-\sqrt{s^2-l^2}}2$$ | (11) |
따라서 최종적으로 직경 s인 절리가 조사창 내에서 양끝내포선 길이 l-dl에서 l사이의 길이를 가질 때 JCV는 식 (12)와 같다. dp는 절리선 계급구간(△l) 차이에 의한 오차를 최소화하기 위해 도입된 변수로 Song(2009)은 △l/1000의 값을 사용하였다.
| $$JCV_{(l,s)}^c=\sin\phi\sum_{p=l-dl}^l\left(\sqrt{s^2-(p-dp)^2}-\sqrt{s^2-p^2}\right)(W-p\cos\theta)(H-p\sin\theta)$$ | (12) |
위 양끝내포선의 방법과 동일하게 한끝내포선, 양끝외포선의 JCV도 정의할 수 있다. 그러나 Fig. 3과 Fig. 4에서 볼 수 있듯이 동일한 한끝내포선 또는 양끝외포선의 길이(l΄)를 가지는 경우에도 절리선 중심의 위치는 무한평면상 절리선 길이(l)에 따라 차이를 보인다. 한끝내포선의 중심점 위치는 Fig. 3에서와 같이 조사창 양쪽에 위치하게 되고, 양끝내포선의 중심점 위치는 Fig. 4에서와 같이 빗금친 영역과 양쪽 모서리 부분에 나타난다.
따라서 l에 대한 적분이 한차례 더 이루어져야 정확한 JCV를 계산할 수 있다. 이러한 과정을 거쳐 정의된 JCV는 다음과 같다. 여기서 G[q, l-△l]은 q와 l-△l 중 큰 값을 의미한다.
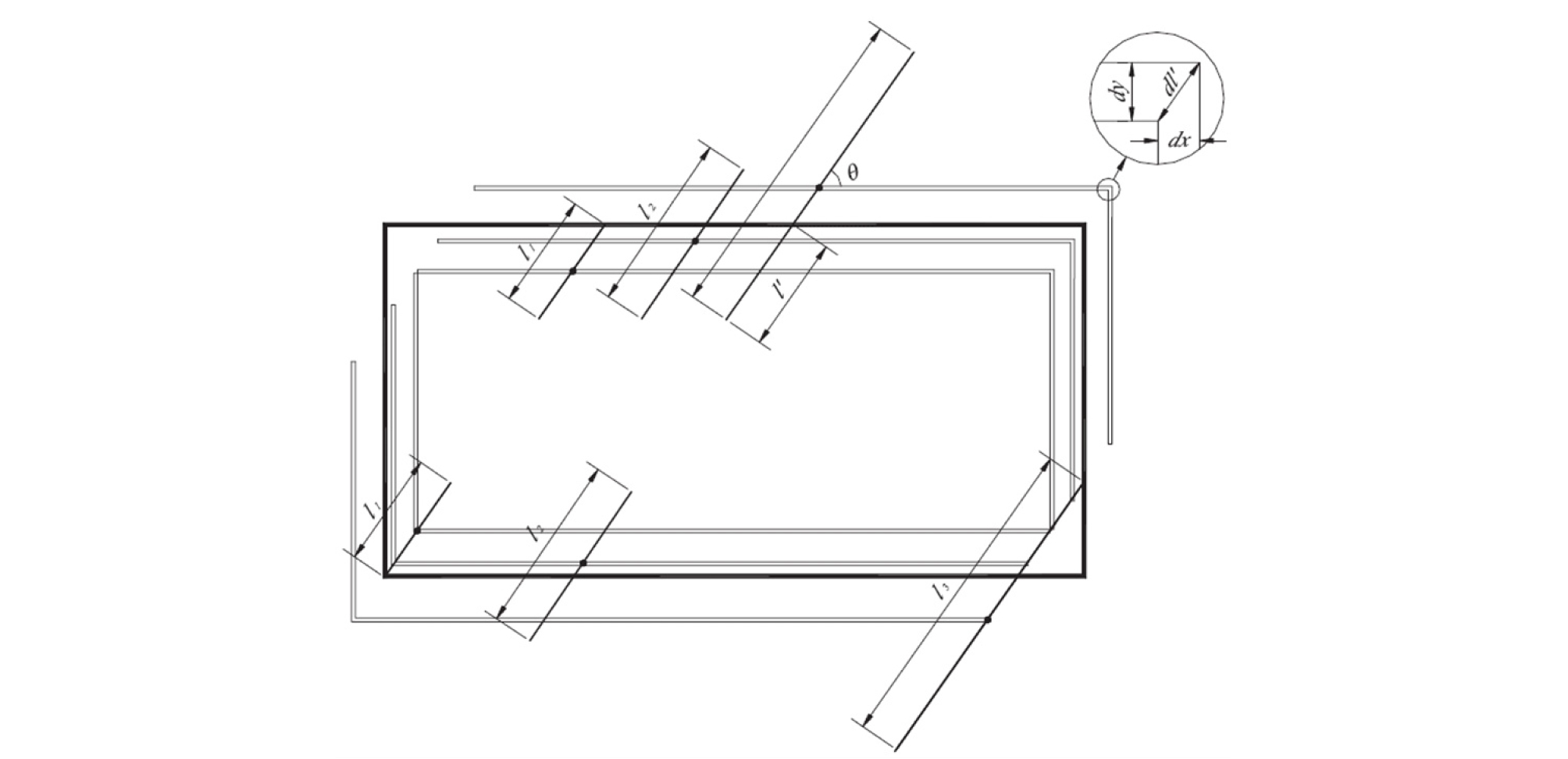
Fig. 3.
The trace center zones of dissecting traces whose partial length within a window is l΄ (Song, 2009)
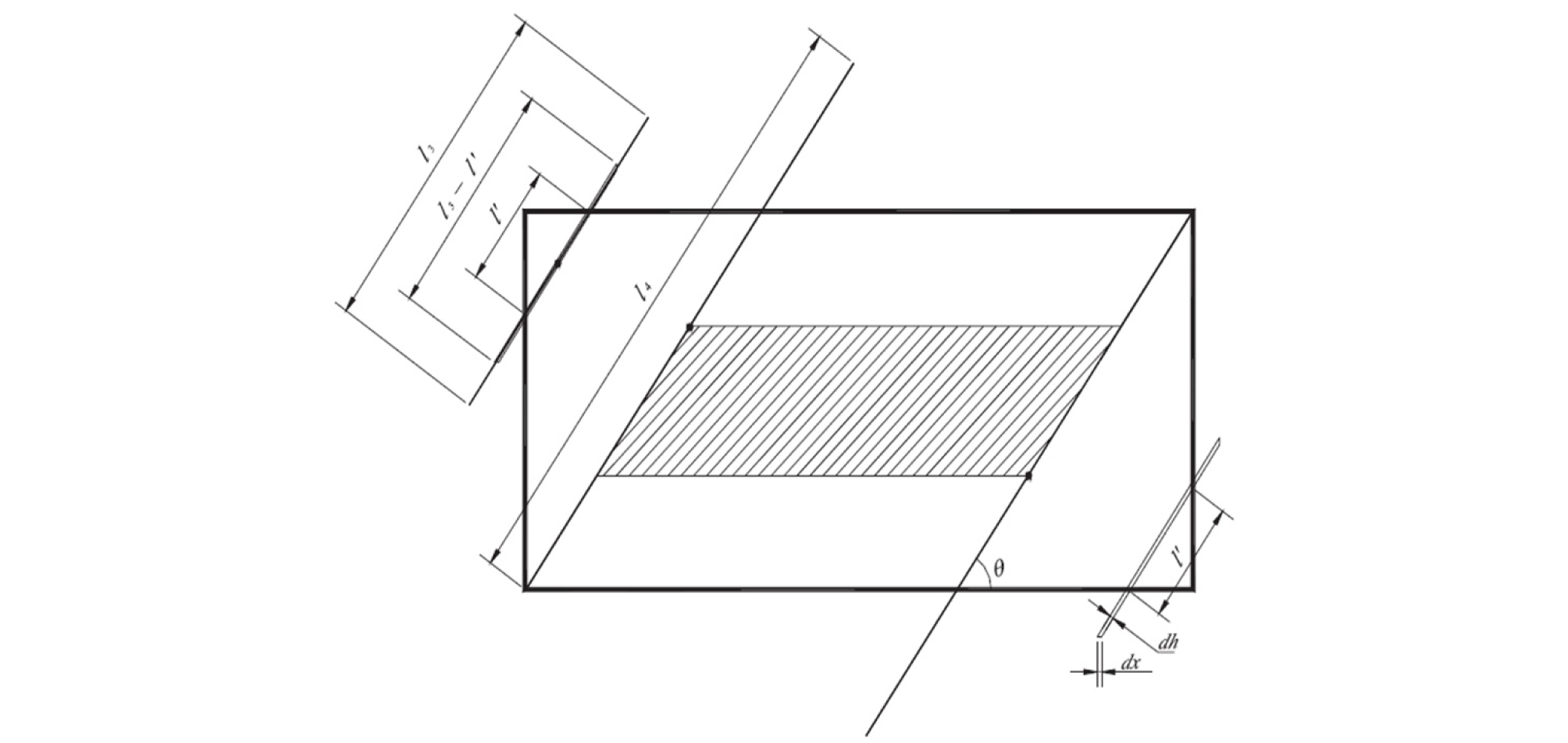
Fig. 4.
The trace center zones of transecting traces according to the whole and partial trace lengths (Song, 2009)
위에서 정의된 JCV(식 (12)~(14))를 앞선 2.1절의 과정에 적용하면 평면조사창에서의 절리 직경분포를 추정할 수 있다. 이 방법은 이론적으로 계산되기 때문에 정확도가 높으며 해석속도가 빠르다는 장점이 있다. 그러나 조사창이 평면이 아닌 경우에 JCV는 불규칙적인 형상을 가지기 때문에 위와 같이 이론적으로 계산하여 도출하는 것이 불가능하다. 따라서 이러한 이론적 JCV 산정법은 평면조사창에서만 적용이 가능하다는 단점이 있다.
2.2.2 전수조사기법
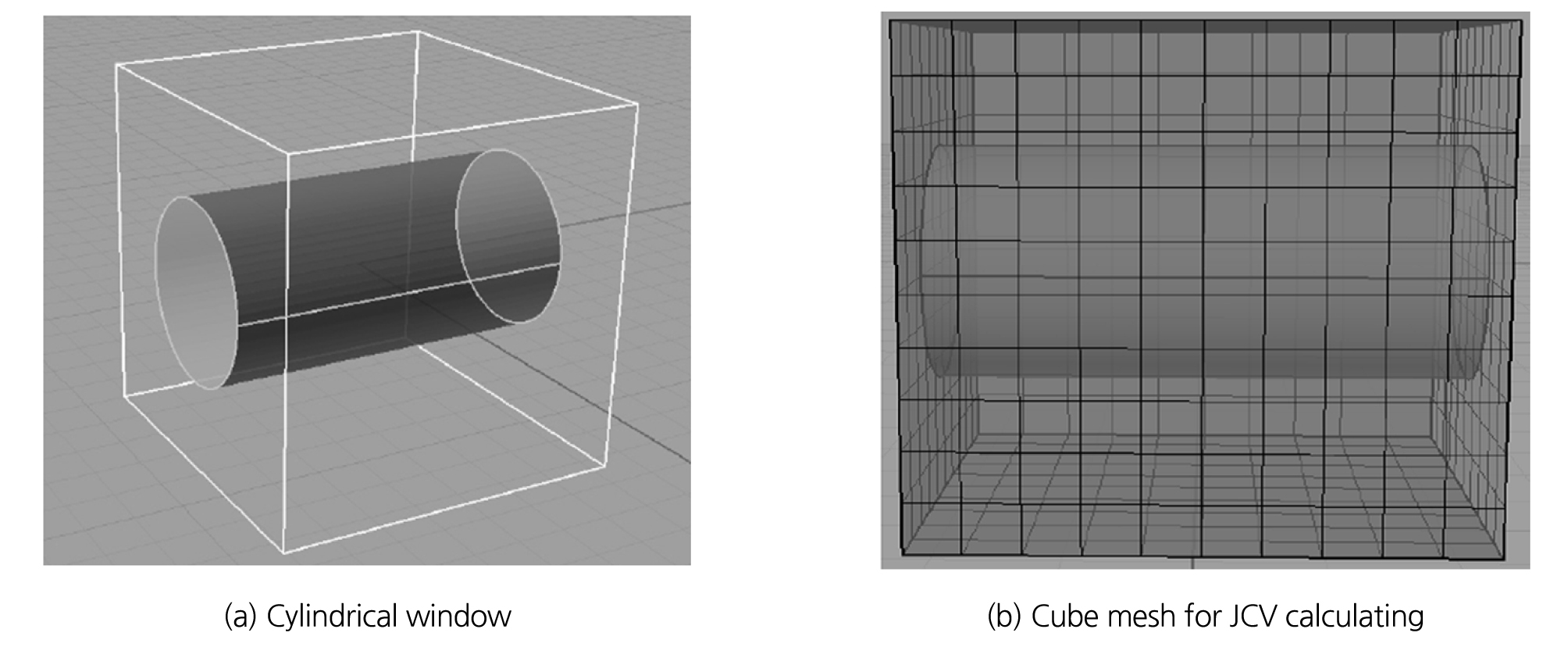
현장 적용성을 높이기 위해 비평면 조사창에서의 JCV를 산정하고자 Jeon et al.(2011)과 Suh and Song(2016)은 조사창을 원통형으로 가정하고, 전수조사기법을 적용하였다. Fig. 5(a)는 원통형 조사창의 형상을 나타내고 있으며, 이를 Fig. 5(b)에서와 같이 수많은 cube mesh (약 100만 개)로 세분화하였다.
세분화된 미세 cube mesh의 중심에 직경이 s인 원판형 절리의 중심점이 위치한다고 가정하고, 모든 mesh에 대해 조사창에 생성되는 절리선의 길이를 측정한다. 이 과정에서 l-dl에서 l 사이의 길이를 가지는 양끝내포선이 측정되는 mesh의 총 개수를 구하고 단위 mesh의 부피를 곱해 JCV(l,s)를 산정하게 된다. 절리 직경(s)을 계급구간 크기만큼 증가시켜가며 반복하면 JCV를 산정할 수 있게 된다.
위와 같은 원통형 조사창에서는 양끝내포선, 한끝내포선, 양끝외포선의 정의가 불명확해진다. 조사창을 관통하는 절리가 있을 수 있으며, 한 절리가 2개의 절리선을 형성할 수도 있기 때문이다. 이러한 이유로 Jeon et al., 2011과 Suh and Song(2016)은 한 절리가 2개의 절리선을 나타내는 경우는 제외하고, 한 절리가 양끝이 모두 보이는 하나의 절리선을 나타내는 경우를 양끝내포선으로 정의하였다. 그리고 이 양끝내포선의 JCV만을 산정하여 절리 직경분포 추정에 이용하였다. 이 방법은 조사창 내에서 나타나는 많은 절리선을 제외하게 되므로 현장상황에 따라 정확도가 많이 떨어지게 된다. 실제로 Jeon et al., 2011의 연구에서는 평균오차율이 20%대에 달했으며, Suh and Song(2016)은 “제1종 프레드홀름 적분방정식(Fredholm integral equation of the 1st kind)”을 활용하는 진동 감쇠 기법을 제안하여 평균오차율을 감소시켰으나 여전히 10%대에 달했다. 이러한 진동 감쇠 기법은 분포가 연속적이지 않은 경우 오히려 오차율을 증가시키는 방향으로 작용하기 때문에 적용 시 주의가 필요하다.
상기 연구 결과들은 하나의 절리에 의해 2개의 절리선이 발생하는 경우를 배제하고 해석한 결과이므로 실제 현장조사를 통해 취득한 절리선 크기분포를 입력값으로 이용하는 경우 오차율이 더욱 증가할 것으로 판단된다.
전수조사기법은 cube mesh의 크기를 작게 할수록 절리 크기분포의 추정 정확도가 증가하지만 해석시간이 과도하게 소요되는 단점이 있다. 또한, 각 계급 사이의 직경 값을 갖는 절리는 JCV 산정 시에 제외되므로 계급 구간의 크기를 작게 할수록 더 정확한 추정이 가능하나, 이 역시 해석시간을 증가시키는 요인이 된다. 예를 들어 계급구간 크기를 1m로 했을 시 1m 직경의 절리에 대한 전수조사 이후 2m 직경의 절리에 대해 전수조사를 하게 되며, 1~2m의 직경을 가지는 절리는 고려되지 못 한다. 본 연구에서는 이러한 단점들을 보완하는 새로운 JCV 산정 기법을 제안하고자 하였다.
3. 새로운 Joint Center Volume (JCV) 산정 기법 제안
3.1 비평면 조사창에서의 절리선 종류
앞서 언급했듯이 비평면 조사창에서는 평면에서와 다르게 절리선의 종류가 다양하게 나타난다. 기본적으로 양끝내포선, 한끝내포선, 양끝외포선으로 정의되기는 하지만 하나의 절리가 2개의 절리선을 발생시킬 수도 있고, 원통형과 같이 연속적으로 이어진 조사창의 경우 조사창 전체를 관통하여 절리선의 끝을 정의할 수 없는 경우도 있다.
본 연구에서는 관찰 가능한 모든 절리선 종류를 고려하기 위하여 다음과 같이 절리선을 10종류로 분류하였다.
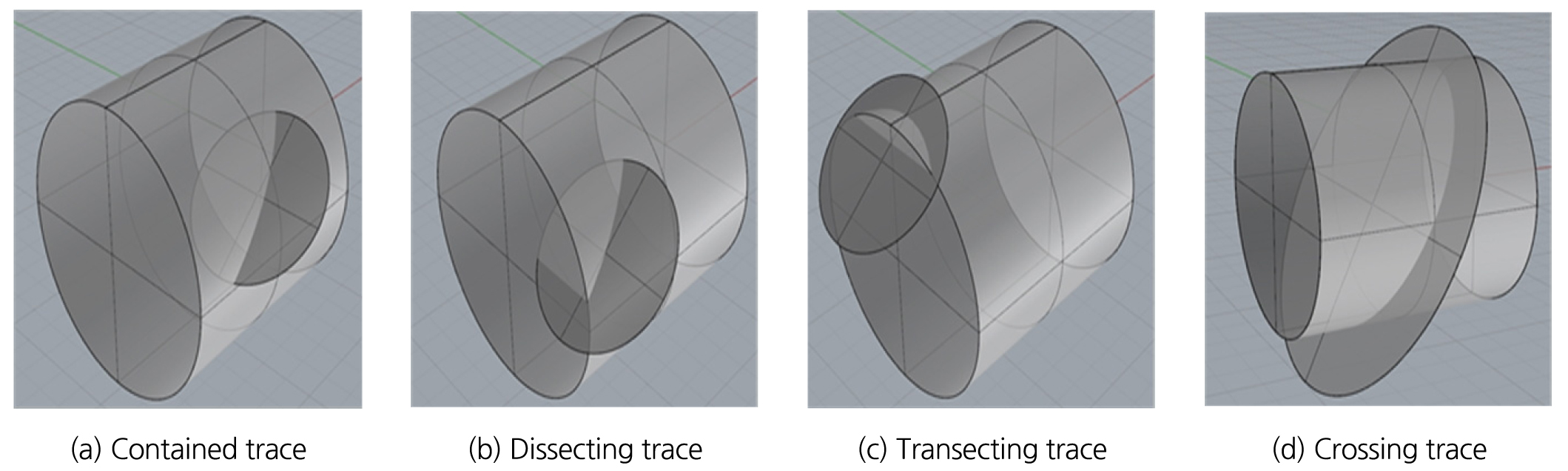
(1) 양끝내포선 (contained trace) (2) 한끝내포선 (dissecting trace)
(3) 양끝외포선 (transecting trace) (4) 관통선 (crossing trace)
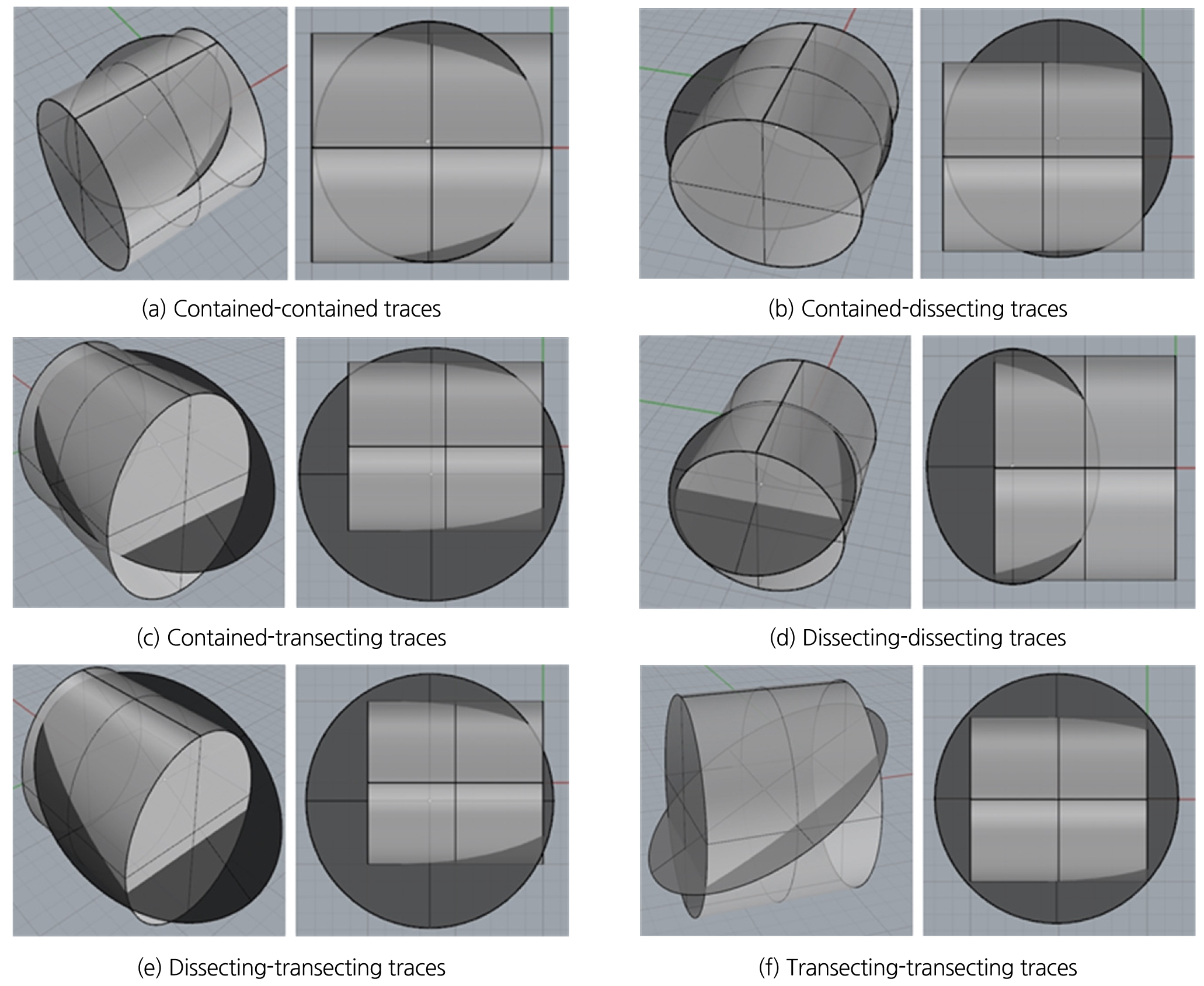
(5) 양끝내포선-양끝내포선 (contained-contained traces) (6) 양끝내포선-한끝내포선 (contained-dissecting traces)
(7) 양끝내포선-양끝외포선 (contained-transecting traces) (8) 한끝내포선-한끝내포선 (dissecting-dissecting traces)
(9) 한끝내포선-양끝외포선 (dissecting-transecting traces) (10) 양끝외포선-양끝외포선 (transecting-transecting traces)
위 절리선 종류에서 (1)~(4)는 하나의 절리가 1개의 절리선을 발생시키는 경우이며, (5)~(10)은 하나의 절리가 2개의 절리선을 발생시키는 경우이다. Fig. 6과 Fig. 7은 원통형 조사창에서 위와 같은 절리선이 발생되는 예시를 나타낸 것이다.
3.2 몬테카를로 시뮬레이션을 이용한 Joint Center Volume (JCV) 산정 기법
본 연구에서는 이론적 산정법의 적용이 불가능한 비평면 조사창에서의 JCV를 산정하는데 있어, 전수조사기법의 한계를 극복하고자 몬테카를로 시뮬레이션을 이용하였다.
식 (3)에서 볼 수 있듯이, JCV는 이산화 과정에서 JCVij와 같이 행렬형태로 정리되며, i는 절리선 계급구간의 개수인 m개, j는 절리 직경 계급구간의 개수인 n개로 나타난다. 이러한 JCV 행렬을 우선 다음과 같이 열벡터들로 나누어 정리하였다. 여기서 아래첨자인 cv는 열벡터(column vectors)를 의미한다.
그리고 식 (3)을 행렬식으로 정리하면 아래와 같이 나타낼 수 있다.
| $$\left[JCV_{ij}\right]\;\left[c_j\right]=\frac1{\lambda_\nu\triangle s}\left[N_i\right]$$ | (17) |
위 관계식에서 절리 직경분포(cj)가 n차원 유클리드 공간(Rn)의 표준기저벡터(n차 단위행렬의 열벡터(e1, e2, ... , en))와 같은 분포를 가진다고 가정한다면 JCV와 표준기저벡터의 곱은 JCV행렬의 각 열벡터로 나타나게 되며, 아래와 같이 간단하게 정리가 가능하다.
| $$JCV_{n,c\nu}=\frac1{\lambda_\nu\triangle s}\left[N_i\right]\;\;\;\;\;\mathrm{if}\;c_j=e_n$$ | (18) |
여기서 절리 직경분포가 n차원 유클리드 공간의 표준기저벡터와 같은 분포를 가진다는 것은 공간상의 절리들이 한 계급구간에서의 직경크기만 가진다는 것을 의미한다. 따라서 각 계급구간별로 해석공간 상에 임의의 개수의 절리를 발생시키고, 이로 인해 조사창 내에 발생되는 절리선의 개수를 구할 수 있다면 식 (18)을 이용하여 JCV 행렬의 모든 열벡터를 구할 수 있게 된다. 해석공간의 크기와 발생 절리의 개수로 체적빈도 λv가 정해지고, 절리 직경 계급구간의 크기로 △s가 정해진다.
이렇게 임의의 개수의 절리를 발생시켜 JCV 행렬을 도출하는 과정을 반복하면 JCV 행렬의 각 요소들이 특정값에 수렴하는 결과를 보인다. 본 연구에서는 이러한 최종 수렴치를 JCV 행렬의 각 요소들로 정의하였으며, 행렬의 대각요소들의 절대값 차이가 0.1 이하로 수렴할 때까지 반복하여 JCV 행렬을 도출하였다. 이 때, 충분한 반복횟수 하에서는 해석공간의 크기와 발생 절리의 개수는 JCV 행렬의 값에 큰 영향이 없는 것으로 나타났다. 그러나 체적빈도가 작을수록 JCV 행렬값이 수렴하는데 더 오랜 시간이 소모되므로 적절한 해석공간의 크기와 발생 절리의 개수를 정해야 하며, 이에 대한 추가적인 분석이 필요할 것으로 보인다.
3.1절에서 분류한 것과 같이 비평면 조사창에서는 총 10종류의 절리선이 발생가능하다. 그러므로 직경분포 예측을 위해서는 각 절리선 종류 별로 10개의 JCV 행렬을 산정하여 이용하는 것이 가장 좋은 결과를 보일 것이다. 그러나 현장에서 관측 가능한 절리선은 종류를 구분하는 것이 일반적으로 불가능하다. 예를 들어, 관측된 양끝내포선은 분류상 양끝내포선(3.1절 분류상 (1))인지 양끝내포선-한끝내포선(3.1절 분류상 (6))에 의해 생긴 절리선인지 구분이 불가능하다.
본 연구에서는 이러한 상황을 고려하여 JCV 산정 시 절리선을 양끝내포선, 한끝내포선, 양끝외포선 3종류로만 구분하고, 하나의 절리가 1개의 절리선을 발생시키는 경우와 2개의 절리선을 발생시키는 경우로 각각 나누었다. 이러한 과정을 통해 10개의 JCV가 아닌 총 6개의 JCV로 모든 절리선의 정보를 종합할 수 있으며, 최종적으로 Table 1과 같이 6개의 JCV 행렬이 산정되게 된다. 여기서 관통선은 양끝외포선에 포함하였다.
Table 1. JCV matrices used in this study
하나의 절리가 2개의 절리선을 발생시키는 경우에는 절리선의 종류에 따라 각각의 JCV 행렬에 반영하게 된다. 예를 들어, 양끝내포선-한끝내포선(3.1절 분류상 (6))의 경우에는 JCVijc(2)와 JCVijd(2)를 산정하는 과정에서 절리선 개수에 각각 포함시킨다. 결과적으로 총 6개의 JCV 행렬이 구해지게 되며, 각각의 JCV 행렬을 이용하여 직경분포 cj를 구할 수 있다. 식 (19)와 식 (20)은 각각 하나의 절리가 1개의 절리선을 발생시키는 경우 양끝내포선을 이용한 관계식과 하나의 절리가 2개의 절리선을 발생시키는 경우 양끝내포선을 이용한 관계식이다.
| $$\left[JCV_{ij}^{c(1)}\right]\;\left[c_j\right]=\frac1{\lambda_\nu\triangle s}\left[N_i^{`c(1)}\right]$$ | (19) |
| $$\left[JCV_{ij}^{c(2)}\right]\;\left[c_j\right]=\frac1{\lambda_\nu\triangle s}\left[N_i^{`c(2)}\right]$$ | (20) |
여기서 Ni΄c(1)은 하나의 절리가 1개의 절리선을 발생시키는 경우에 양끝내포선의 개수이며, Ni΄c(2)는 하나의 절리가 2개의 절리선을 발생시키는 경우에 양끝내포선의 개수이다. 즉, 이 두 항을 더하면 현장에서 관측되는 모든 양끝내포선의 개수(Ni΄c)가 된다. 이를 이용하기 위해 다음과 같이 식 (19)와 식 (20)을 더하여 식을 정리하였다.
따라서 양끝내포선과 관련된 두 가지 JCV(JCVijc(2), JCVijc(1))를 산정할 수 있다면 현장에서의 양끝내포선 개수를 이용하여 직경분포 추정에 활용할 수 있다. 한끝내포선, 양끝외포선도 동일한 과정으로 정리될 수 있다.
그러므로, 위 6개의 JCV 행렬을 다음과 같이 3개로 정리하여 활용할 수 있다.
① 양끝내포선 JCV 행렬: JCVijc=JCVijc(1) + JCVijc(2)
② 한끝내포선 JCV 행렬: JCVijd=JCVijd(1) + JCVijd(2)
③ 양끝외포선 JCV 행렬: JCVijt=JCVijt(1) + JCVijt(2)
이 세가지 JCV 행렬은 3.1절의 모든 절리선 종류를 포함하고 있으며, 이를 활용하면 현장에서 하나의 절리가 1개의 절리선을 나타내는지 2개의 절리선을 나타내는지에 대한 구분이 필요가 없다는 장점이 있다.
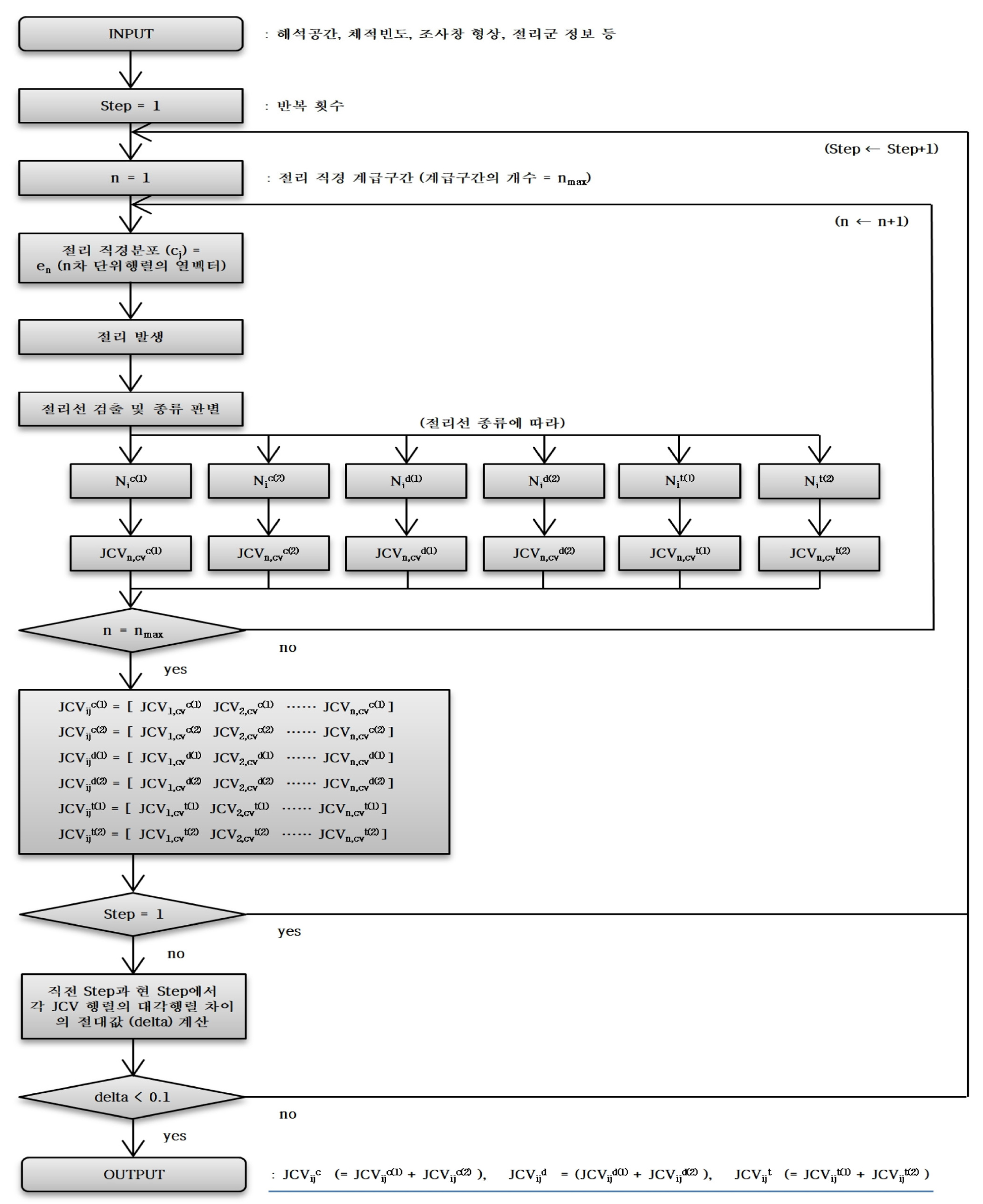
본 연구에서는 matlab을 이용하여 이러한 알고리즘을 구현하였으며, 전체적인 JCV 산정 알고리즘은 Fig. 8과 같다.
위 과정은 현장에서 조사되는 절리선 종류를 양끝내포선, 한끝내포선, 양끝외포선의 3종류로만 구분하면 되기 때문에 직경분포 추정 시 모든 절리선 종류를 이용할 수 있다. 또한, JCV 산정 시 절리 직경계급 구간 사이의 값을 임의로 발생시키기 때문에 계급구간 크기에 따라 제외되는 직경크기가 존재하지 않는다는 장점이 있다.
4. 적용성 검토
제안된 JCV 산정 기법의 절리 직경분포 추정 시 적용성을 살펴보고자 하였다. 직경분포 추정은 Song(2009)에 의해 제안된 기법을 사용하였으며, 식 (9)에서와 같이 가중치벡터를 적용한 오차제곱을 최소화하는 직경분포(cj)를 추정하였다.
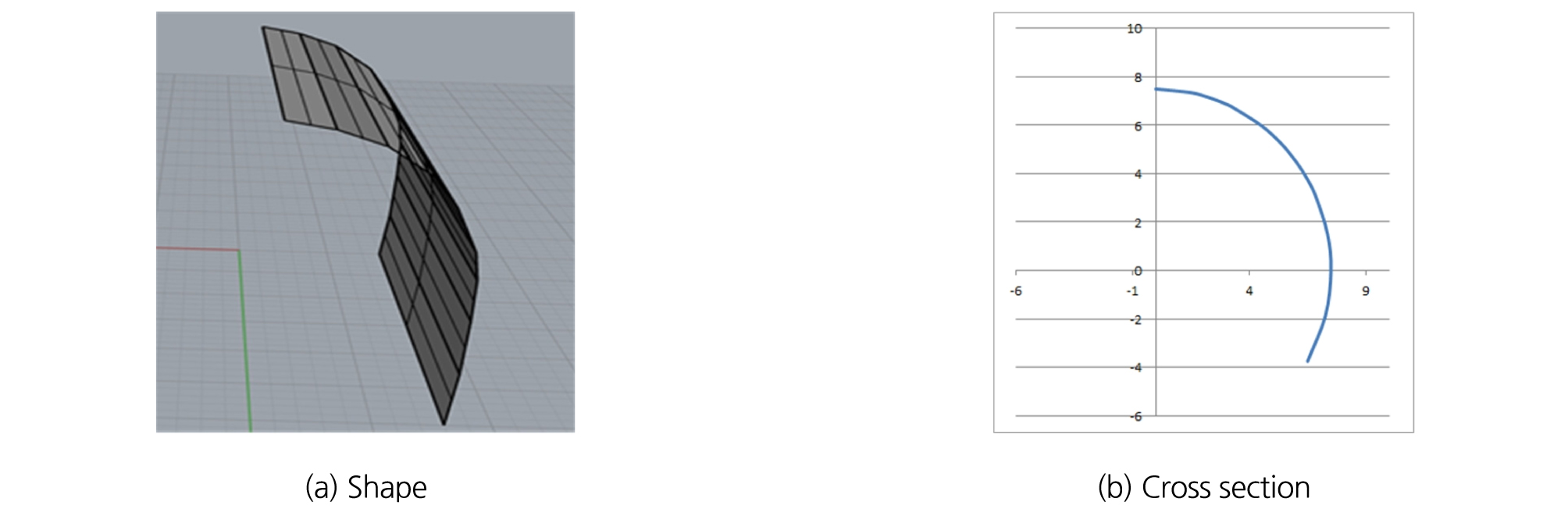
적용성 검토를 위한 조사창은 Fig. 9와 같은 곡면 조사창과 Fig. 10과 같은 터널형(마제형) 조사창을 이용하였으며, 축방향으로의 깊이는 모두 20m으로 하였다. JCV 산정 시 최대 직경크기는 15m 로 한정하였으며, 해석공간은 최대크기 직경을 가지는 절리가 조사창과 만나는 지점까지로 설정하였다. 그리고 체적빈도는 단위부피당 약 0.5개의 절리 중심이 위치하도록 하였으며, 절리 직경 계급과 절리선 계급의 크기는 모두 1로 설정하였다.
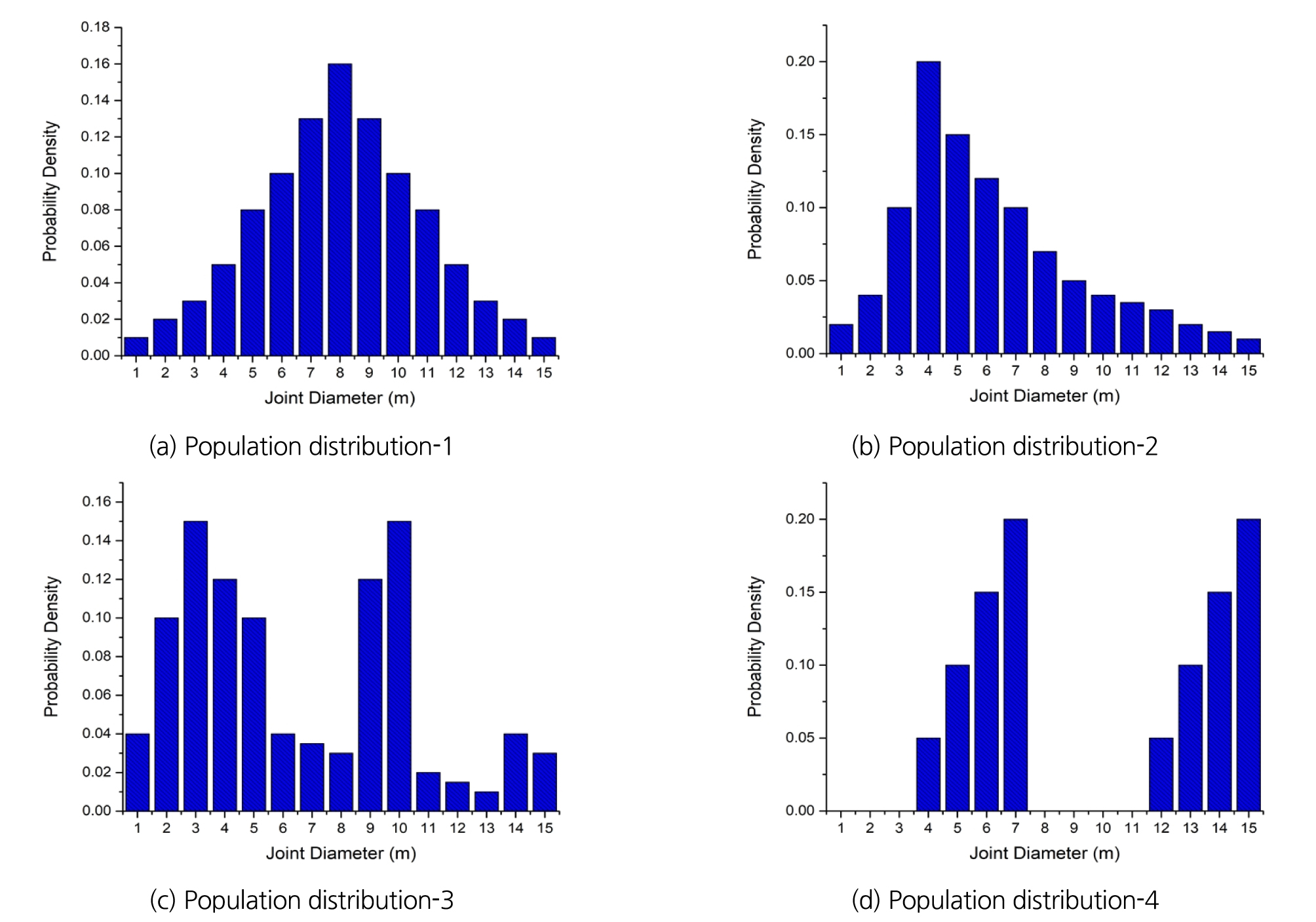
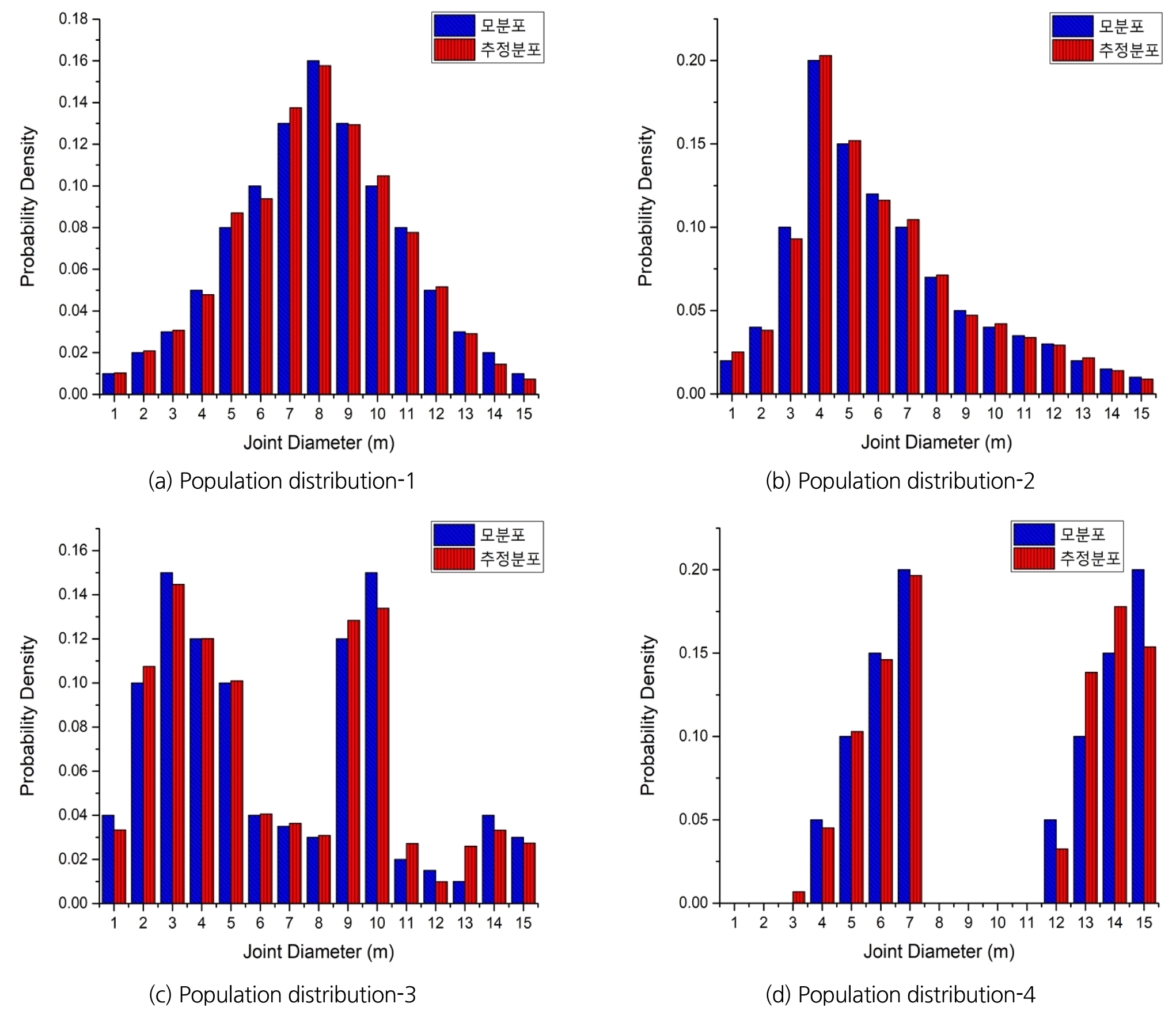
현장에서는 정확한 모분포 획득이 불가능하므로 몬테카를로 시뮬레이션을 적용하여 검증과정을 수행하였다. 해석공간상에 특정분포를 따르는 가상의 절리군을 발생시키고, 이로 인해 조사창에서 검출되는 절리선 조사 결과를 이용하여 예측한 추정분포와 모분포를 비교하였다. 각 조사창마다 Fig. 11과 같은 4가지의 모분포를 가지는 가상의 절리군을 발생시켜 결과를 분석하였으며, 절리군은 180도의 dip direction과 40도의 dip을 갖도록 하였다.
모분포-1은 자연계 현상에서 가장 일반적인 정규분포(normal distribution)을 가정한 것이며, 모분포-2는 절리선 길이분포 가정 시 많이 활용되는 대수정규분포(log-normal distribution)을 가정한 것이다. 이는 절리 크기(직경)분포 역시 이러한 일반적인 분포를 따를 가능성이 높다고 판단하였기 때문이다. 모분포-3과 모분포-4는 분포가 불규칙하거나 분산되어 있는 특수 경우에 추정 정확도를 분석하여 보고자 설정하였다.
검증을 위한 몬테카를로 시뮬레이션 시에는 절리 개수가 적을 시에도 적용 가능한지 살펴보기 위해, 체적빈도를 단위부피당 약 0.2개의 절리가 존재하는 것으로 변경하여 수행하였다. 그리고 관측오차(sampling bias)를 최소화하기 위해 최소 200회 이상의 절리선 측정 결과를 평균하여 이용하였다. 관측오차와 관련하여서는 본 연구의 목적을 벗어나기 때문에 영향을 배제하고자하였으며, 향후 추가적인 연구가 요구되는 부분이다.
최종 행렬식의 수치계산 시에는 Gauss-Seidel 기법에서 수렴속도를 감속시키는 연속하향이완(Successive Under Relaxation, SUR)법을 적용하였다. SUR법은 임의의 해로부터 반복적으로 오차를 계산하여 최소의 오차를 보이는 값으로 수렴된 해를 도출한다. 본 연구에서 도출하고자하는 것은 절리 직경분포의 확률밀도이므로, 수치계산의 해 중에서는 음수가 존재해서는 안 된다. 따라서 SUR법에 의한 반복과정에서 음수가 나타날 시 임의적으로 수정할 수 있도록 알고리즘을 보완하여 항상 양수의 해만을 나타내도록 하였다.
4.1 곡면 조사창 추정결과
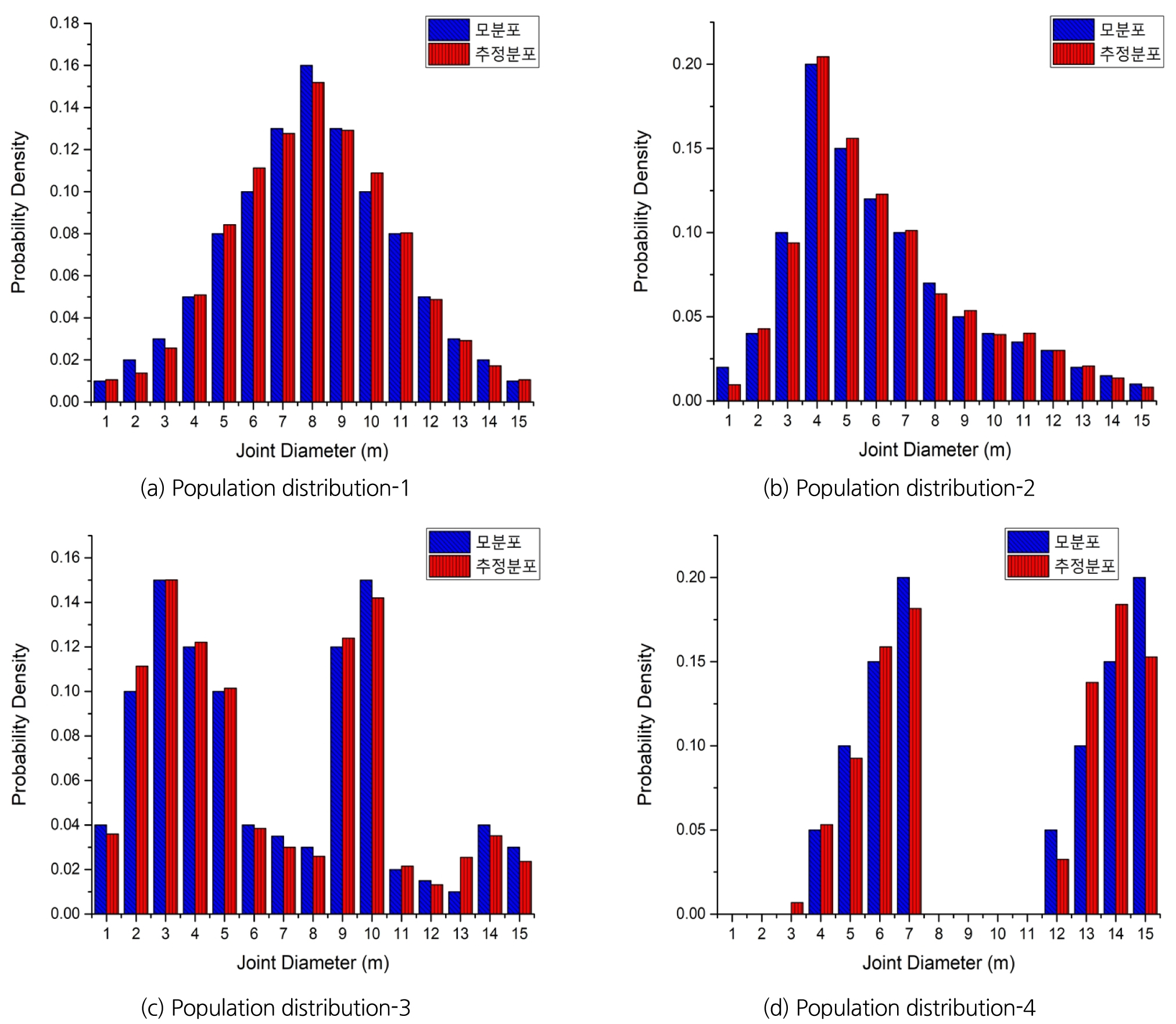
곡면 조사창에서의 직경분포 추정결과는 Fig. 12에 나타낸 것과 같으며, 다양한 모분포를 합리적으로 추정 가능하였다.
Table 2는 각 모분포 별 오차율을 나타낸 것이다. 여기서 오차율은 모분포와 추정분포 사이의 절대값 차이를 모두 합산한 것으로 정의하였다. 오차율 분석결과, 분포가 분산되어 있는 모분포-4의 경우를 제외하고는 모두 10% 이하의 오차율을 보였다.
Table 2. Error rates of estimation in curved window
| Population distribution-1 | Population distribution-2 | Population distribution-3 | Population distribution-4 | |
| Error rate (%) | 5.38 | 5.40 | 7.16 | 18.10 |
4.2 터널형 조사창 추정결과
터널형 조사창의 경우에도 곡면 조사창과 유사한 결과를 보였으며, 오차율 역시 모분포-4의 경우를 제외하고는 모두 10% 이하로 나타났다. 이 결과는 Fig. 13과 Table 3에 나타내었다.
Table 3. Error rates of estimation in horseshoe window
| Population distribution-1 | Population distribution-2 | Population distribution-3 | Population distribution-4 | |
| Error rate (%) | 4.54 | 3.92 | 8.54 | 15.20 |
4.3 추정결과에 대한 논의
곡면 조사창과 터널형 조사창에서의 절리 직경분포 추정 결과를 살펴보면, 분포가 분산되어 있는 모분포-4의 경우를 제외하고는 모두 10% 이하의 오차율을 보였다. 이는 기존 Jeon et al.(2011), Suh and Song(2016)의 결과와 비교해 보았을 때, 제안된 JCV 산정 기법을 적용 시 더욱 신뢰도 있는 추정 결과를 도출한다고 볼 수 있다.
그러나 분포가 분산되어 있는 모분포-4와 같은 경우에는 오차율이 급격히 증가하는 경향을 보였으며, 이에 대해서는 추가적인 보완이 필요할 것으로 보인다. 또한, 본 연구에서의 결과는 최대 절리직경 크기, 조사창 크기, 해석공간 등이 한정적으로 적용되었기 때문에 다양한 조건 하에서 분석이 추가적으로 수행된다면 JCV 산정 기법의 완성도를 높일 수 있을 것으로 판단된다.
5. 결 론
본 연구에서는 절리 크기(직경)분포 추정 시 활용되는 JCV를 산정하는 새로운 기법을 제안하였다. 몬테카를로 시뮬레이션을 이용한 새로운 JCV 산정법은 Song (2009)에 의해 제안된 평면 조사창에서의 이론적 산정법과는 달리 조사창 형상에 상관없이 모든 비평면 조사창에 적용이 가능하다는 장점이 있다. 또한 Jeon et al.(2011), Suh and Song(2016)에 의한 전수조사기법과 비교하여 모든 절리선 종류 및 절리 직경크기를 고려할 수 있어 더욱 신뢰도 있는 직경분포 추정이 가능하며, 해석시간 측면에서도 이점이 있다.
제안된 JCV 산정법의 적용성을 검증하기 위해 곡면 조사창과 터널형(마제형) 조사창에 대해 각각 4가지 모분포를 가지는 절리군을 발생시켜 Song (2009)이 제안한 알고리즘을 바탕으로 직경분포를 추정해 보았으며, 다양한 분포를 신뢰도 있게 추정 가능하다고 판단되었다. 그러나 분산도가 높은 특정 분포의 경우 오차율이 급격하게 증가할 수 있을 것으로 분석되어 이에 대한 개선이 필요할 것으로 보인다. 또한 다양한 조건 하에서의 추가 검증 과정을 통해 JCV 산정 기법의 완성도를 높일 수 있을 것으로 판단된다.