1. 서 론
2. 입자 접촉조건 검정을 위한 삼축압축시험 모델링
3. EPB TBM 굴진해석 모델링
3.1 Wall 요소를 통한 입자 압밀
3.2 Wall-zone 연계를 통한 입자 압밀
3.3 지반모델 내 TBM 설치
4. EPB TBM 굴진해석 수행 및 결과
5. 결 론
1. 서 론
터널 기계화 시공법이 보편화되며 TBM의 굴진 성능을 사전에 예측하는 것은 터널 설계 단계에서 TBM 장비의 구성을 계획하여 실제 현장에서 시공성과 경제성을 확보하기 위한 필수 요소가 되었다. TBM 굴착성능의 예측은 현장 TBM 굴진 데이터나 실내 모형시험을 통해 경험적・간접적으로 파악하는 것이 대부분이지만 공사의 규모가 커 실험이나 현장에서 얻을 수 있는 데이터가 상대적으로 적어 이를 수치해석(numerical analysis)적으로 접근하고자 하는 시도가 증가하고 있다. 특히 현장이 많지 않아 현장 데이터가 부족한 국내 여건에서는 수치해석적 도구(tool)를 제안하는 것이 더욱 중요하다고 할 수 있다. 그러나 TBM 굴진 모델링은 TBM과 지반재료의 실시간 상호작용을 고려해야 하고 전방 굴착 지반을 쉽게 예측할 수 없다는 불확실성에서 어려움이 있다. 특히 토압식(EPB, earth pressure balance) TBM의 경우 챔버 또는 스크류 컨베이어와 굴착토의 거동을 추가적으로 고려해야 하므로 이를 위한 명확한 수치해석 방법은 정립되지 않은 상황이다.
TBM 굴진을 수치해석적으로 모사하기 위해 현재까지 유한요소법(FEM, finite element method) 또는 유한차분법(FDM, finite difference method)이 가장 많이 적용되었다(Hasanpour, 2014, Kim et al., 2018, Lambrughi et al., 2012, Nematollahi and Dias, 2019). 그러나 TBM을 이용한 굴착은 전술한 바와 같이 기계와 지반재료와의 동적인 상호작용이라고 할 수 있어 위 방법으로는 굴착에 의한 토크, 추력, 챔버압 등의 실시간 굴진 데이터들을 취득할 수 없어서 유한요소법이나 유한차분법은 명확한 해법이 될 수 없다. 최근에는 컴퓨터 성능의 발전으로 실제 TBM 굴진 거동을 가장 근접하게 모사할 수 있는 개별요소법(DEM, discrete element method)이 적극적으로 활용되고 있다. Maynar and Rodríguez (2005)는 TBM 굴진모사에 개별요소법을 적용하였으며, Wang et al. (2019)은 개별요소법을 활용하여 굴진면의 안정성을 해석하는 연구를 수행하였다. 쏘일 컨디셔닝(soil conditioning)을 고려하기 위해 슬럼프 시험을 모사하여 입자 간 접촉 마찰계수를 수정하는 방식으로 컨디셔닝을 고려한 TBM 굴진해석 연구 또한 수행된 바 있다(Hu et al., 2020, Qu et al., 2019). 최근 5년간 국내에서 TBM 굴진을 모사하기 위한 개별요소법을 활용하는 연구가 수행되었다(Choi et al., 2018, Choi et al., 2019, Lee et al., 2017a, Lee et al., 2017b, Lee et al., 2019a, Lee et al., 2019b). 그러나 개별요소법 만으로 모델링하여 해석을 진행하는 경우 지반의 물성을 직접 입력할 수 없고 입자 접촉물성을 결정하기 위해 추가 검정(calibration)과정이 필요하여 해석에 있어 오차가 크게 발생할 수 있다는 단점을 가지고 있다. 또한 굴착 대상이 되는 지반을 모델링 하기 위해 해석에 사용되는 입자의 개수가 많아지면 해석량이 기하급수적으로 늘어난다는 큰 단점 역시 존재한다.
위와 같은 개별요소법 해석의 단점을 보완하기 위해 본 연구에서는 기존 개별요소법 해석에서 입자에 의해 이루어진 지반의 일부를 유한차분법으로 대체하는 방법으로 개별요소법과 유한차분법을 연계한 EPB TBM의 굴진 수치해석 모델을 제시하였다. 제안된 모델의 경우 개별요소법과 유한차분법을 함께 사용하여 지반을 모델링함으로서 개별요소법만을 사용하였을 경우에 비해 사용되는 입자의 개수를 크게 줄여 해석 효율을 크게 증가시켰으며, 유한차분법으로 구성한 지반의 응력조건을 모사하기 위해 추가적으로 수평응력계수를 고려한 지중응력 분포를 구현하였다. 완료된 해석모델을 검증하기 위해 임의의 굴진율, 커터헤드 및 스크류 컨베이어 회전속도 등의 굴진조건을 결정하여 굴진해석을 수행하여 토크, 추력, 챔버압, 배토량이 유의미하게 나타나는 것을 확인하였다. 본 논문의 개별요소법-유한차분법 연계해석 모델링을 위해 개별요소법 상용 해석 프로그램으로는 PFC3D(ver 6.0)을 사용하였으며(Itasca, 2019), 유한차분법 상용 해석 프로그램의 경우 FLAC3D(ver 7.0)을 사용하였다(Itasca, 2020).
2. 입자 접촉조건 검정을 위한 삼축압축시험 모델링
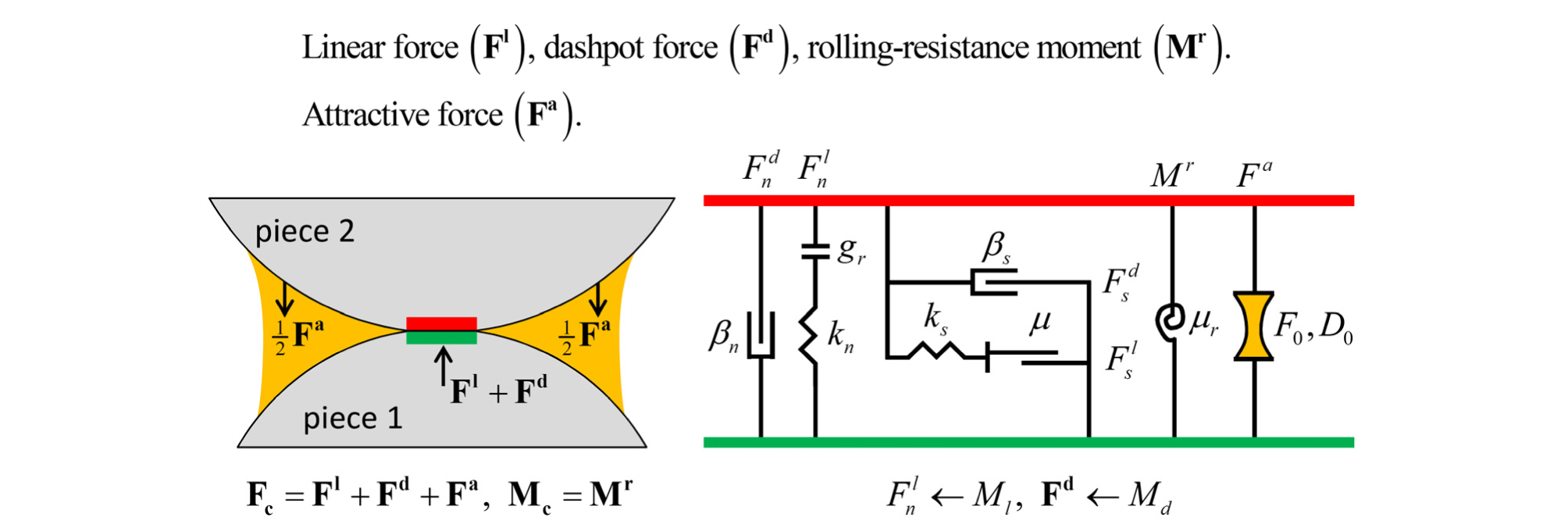
전술한 바와 같이 개별요소법을 기반으로 한 수치해석은 여타 해석방법과는 다르게 직접 내부마찰각이나 점착력 같은 지반 물성치를 입력할 수 없다. 따라서 입자들의 접촉물성을 결정하는 일련의 검정과정을 거쳐야 한다. 본 논문에서는 입자 접촉물성의 결정을 위한 검정과정으로 삼축압축시험을 선택하여 모델링한 후 일련의 삼축압축시험을 수행하였다. 삼축압축시험과 같은 해석을 수행하기 위해서는 입자의 접촉모델의 선정이 선행되어야 한다. 본 논문에서는 화강풍화토와 같은 점착력을 가진 입자의 거동을 재현하기 위해 adhesive rolling resistance linear 접촉모델을 사용하였다. 일반적인 본딩(bonding) 기반 접촉모델의 경우 본딩이 파괴된 후 입자가 다시 접촉할 때 본딩이 생성되지 않아 점착력을 가진 재료 거동을 모사하는데 어려움이 있었다. 그러나 본 논문에서 고려한 모델의 경우 입자 간 거리가 멀어저 점착력이 파괴되어도 일정거리 내에 입자가 근접하면 다시 선형적으로 점착력이 발현된다. adhesive rolling resistance linear 접촉모델에 사용되는 입자의 물성은 유효탄성계수(effective modulus, E*), 수직강성(normal stiffness, kn), 수평강성(shear stiffness, ks), 마찰계수(friction coefficient, μ), 구름마찰계수(rolling friction coefficient, μr), 수직임계감쇠비(normal critical damping ratio, βn), 전단임계감쇠비(shear critical damping ratio, βs), 최대인력(maximum attractive force, F0), 인력범위(attraction range, D0)가 있으며 접촉모델의 개요는 Fig. 1에 나타냈다.
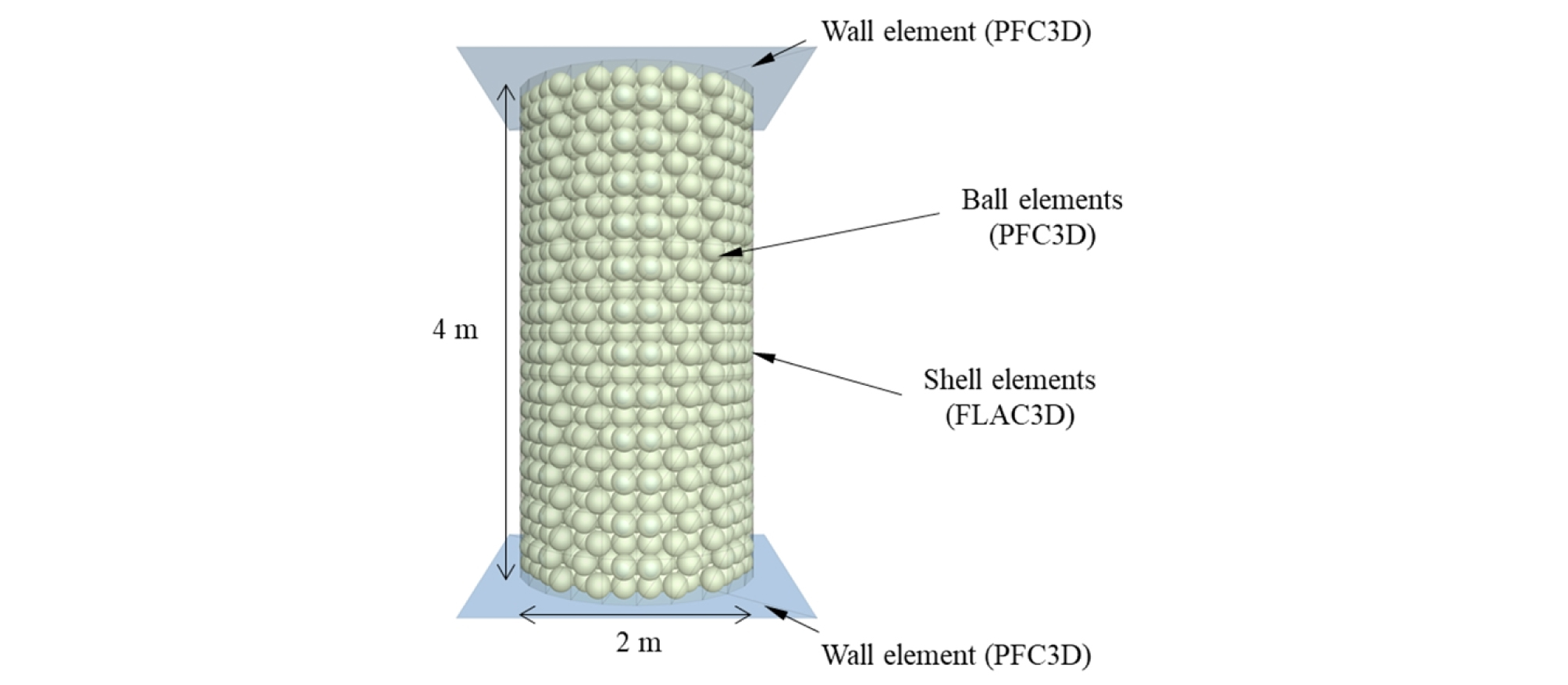
본 논문에서 입자 접촉조건 검정 과정에 사용한 삼축압축시험 모델을 Fig. 2에 나타냈다. 시료 조성을 위한 입자는 0.1 m의 반지름을 가지는 단일입자로 설정하여 ball 요소로 생성하였다. 이는 TBM 굴진 모델에서 사용할 커터헤드 스포크(spoke) 사이의 간격과 스크류 컨베이어의 규격을 고려한 것이며 굴진 해석 효율을 고려한 적정 입자의 크기이다. 본 논문과 같이 단일 입자를 선택할 경우 입자의 적층(packing)을 결정하는 것은 지반 조성 시 모델의 수렴성과 입상체 자체의 강도를 결정하는데 매우 중요하다. 따라서 본 논문에서는 육방조밀적층(Hexagonal closet packing)을 사용하여 입자를 조성하였다. 삼축압축시험 시료의 직경은 2 m, 높이는 4 m 이며, 입자의 밀도는 2637 kg/m3으로 약 2100개의 입자가 형성되었다. 시료에 구속압을 가하기 위한 멤브레인의 역할을 하는 shell 요소의 경우 1400 kPa의 탄성계수, 6 mm의 두께, 90 kg/m3의 밀도를 적용하였다. 125, 250, 375, 450 kPa의 구속압 하에 0.03 %/min의 재하속도로 상부 wall 요소를 이동시켜 삼축압축시험을 수행하였다.
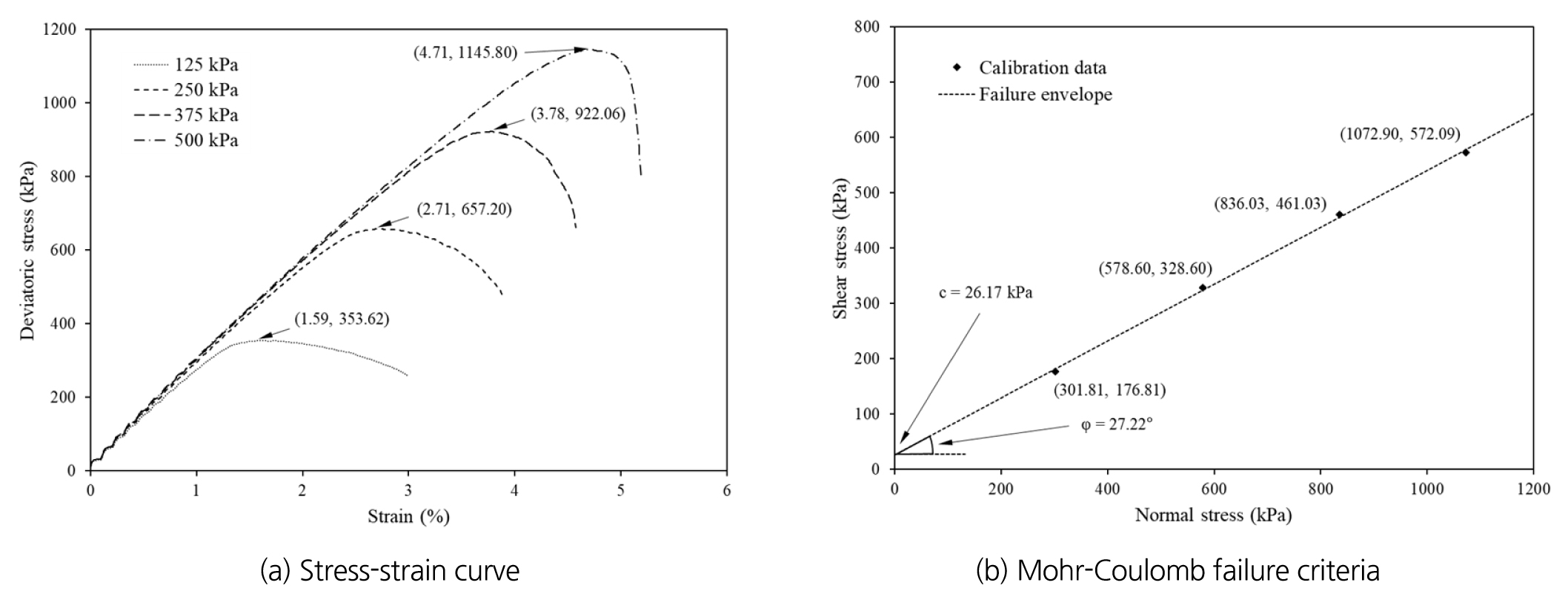
본 논문에서는 내부마찰각 27.3°, 점착력 26.3 kPa의 물성을 가지는 임의의 화강풍화토를 재현하고자 하였으며 상기 해석 조건에 대해 시행착오법(trial and errror)을 통해 삼축압축시험을 수행하고 입자의 접촉물성을 결정하였다. 삼축압축시험의 해석 결과가 Fig. 3에 나타나있다. Fig. 3(a)의 경우 각 구속압 조건에서 변형율에 대한 축차응력 값을 나타낸 그래프이고 이를 통해 Mohr-Coulomb 파괴포락선을 도출한 결과가 Fig. 3(b)에 도시되어 있다. 최대 축차응력의 경우 모두 변형율 5% 이내에서 나타났으며 추세선을 통해 Mohr-Coulomb 파괴포락선을 도출한 결과 내부마찰각 27.22°, 점착력 26.17 kPa를 나타내어 내부마찰력과 점착력 모두 목표 값 대비 오차율 0.5% 이내의 값을 나타냈다. 최종적으로 도출한 adhesive rolling resistance linear contact model의 접촉물성이 Table 1에 정리되어 있다.
Table 1.
Calibration results: contact properties of adhesive rolling resistance linear model
3. EPB TBM 굴진해석 모델링
본 논문에서는 EPB TBM 굴진해석 모델링을 위해 임의의 지반을 가정하였다. 해석 대상 지반은 약 23 m 두께의 풍화토를 모사하고자 하였으며, 풍화토 하부에는 기반암이 존재한다. TBM 굴진은 심도 19 m 지점(약 16 m 토피고) 에서 6.14 m 급 직경의 스포크 타입 EPB TBM이 PFC3D를 통해 구현된 개별요소법 구역으로 굴진하는 것으로 가정하였다. 직접적인 굴착이 이루어지는 개별요소법 구역의 외부는 FLAC3D를 통해 구현된다.
모델링은 다음과 같은 순서로 이루어진다. 첫 번째, PFC3D의 ball 요소를 통해 개별요소법 구역의 입자를 생성하고 6개의 wall 요소를 통해 지중응력 상태에 가깝게 압밀시킨다. 두 번째, 압밀된 개별요소법 구역 주변에 FLAC3D의 zone을 생성시키고 wall-zone 연계를 통해 초기지중응력이 적용된 zone의 자중을 wall을 통해 개별요소법 구역에 전달시켜 압밀한다. 마지막으로 TBM 장비 모델을 정해진 좌표에 위치시킨 뒤 모델링을 완료한다. 각 과정에 대한 상세가 다음 절에 서술되어있다.
3.1 Wall 요소를 통한 입자 압밀
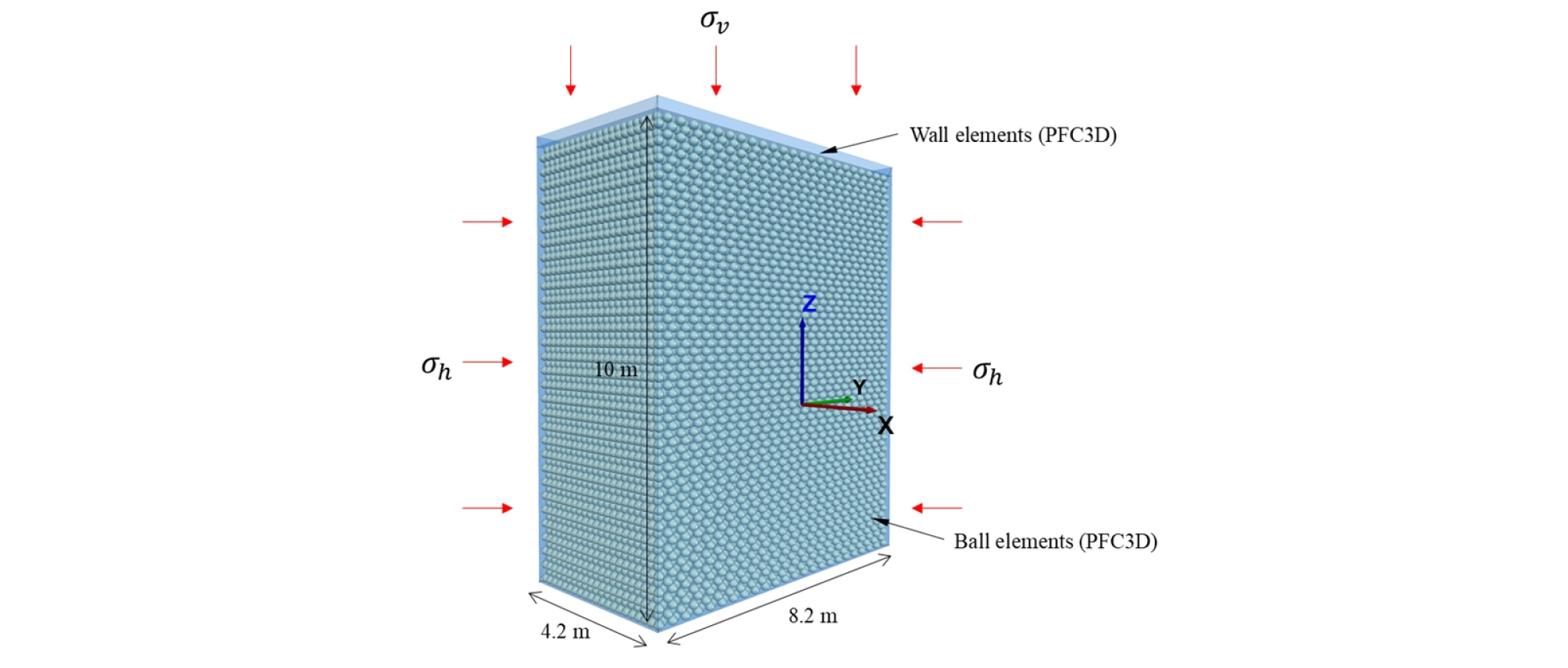
모델링의 첫 번째 단계인 PFC3D의 wall 요소를 통한 압밀과정이 Fig. 4에 나타나 있다. 조성된 ball 입자는 8.2 m(가로), 4.2 m(세로), 10 m(높이)의 크기로 검정에 사용된 삼축압축시험의 경우와 동일하게 단일입자로 육방조밀적층 방식으로 생성되었다. 입자의 접촉물성 또한 Table 1의 검정된 물성 값으로 적용되었다. 지반 조성을 위한 압밀을 수행하기 위해 조성된 입자의 주변에 6개의 wall을 생성하였다. 생성된 wall은 서보컨트롤(servo-control)을 통해 입력된 힘을 유지하며 입자를 압밀시킬 수 있다. 본 논문에서는 6개의 wall 중 하부 wall과 원점이 위치한 면의 wall을 제외한 4개의 wall을 서보컨트롤 하여 ball 입자를 압밀시켰다. 이때 상부 wall의 경우 19.5 kN/m3 단위중량을 가진 상부지반의 상재하중을 입력하여 압밀하였고, 나머지 3개 wall의 경우 0.5의 수평응력계수를 적용하여 평균 수평응력으로 재하・압밀하였다. 평균 수평응력으로 압밀하였기 때문에 첫 번째 압밀 단계 이후 실제 선형적인 수평 지중응력은 모사되지 않는다.
3.2 Wall-zone 연계를 통한 입자 압밀
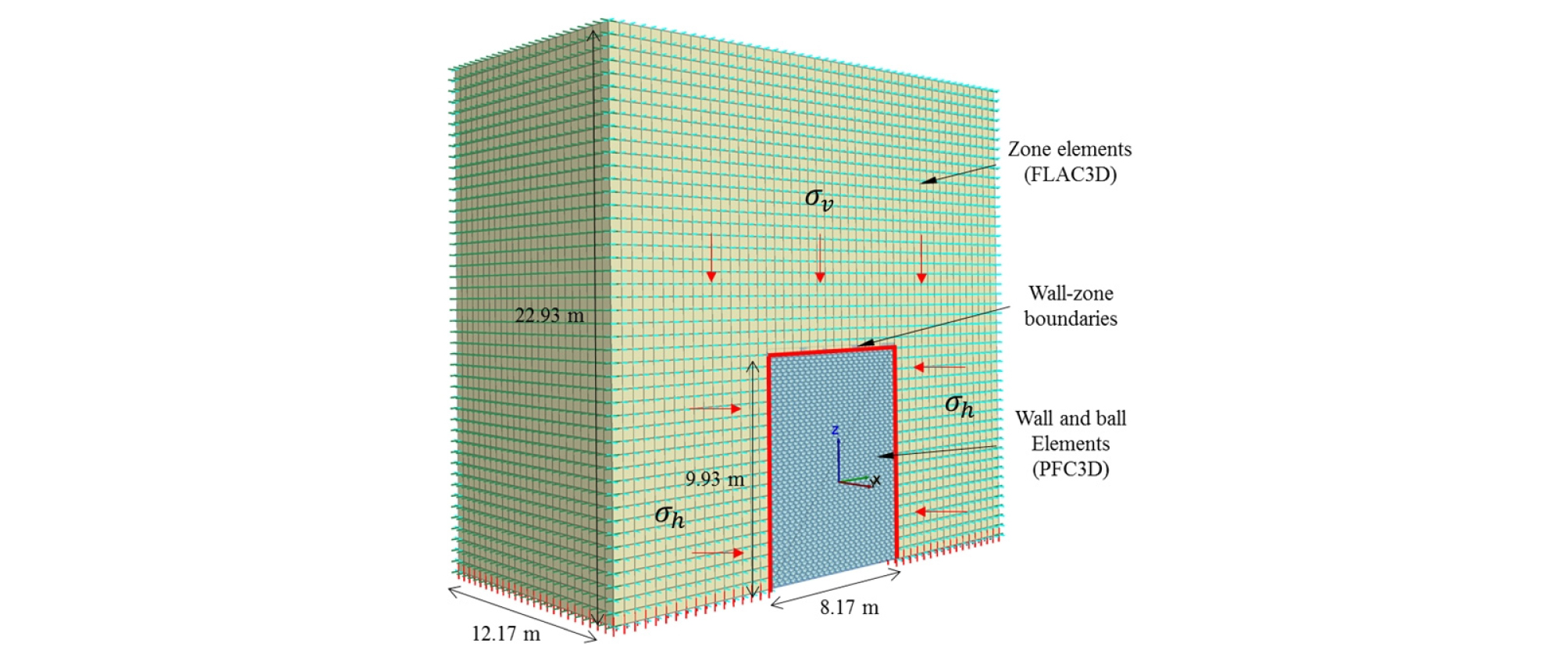
두 번째로는 wall-zone 연계를 통하여 압밀을 진행한다. 이 과정을 통해 수평응력계수를 고려한 수평지중응력을 구현할 수 있으며, TBM 굴착이 이루어지는 개별요소법 구역을 제외한 유한차분법 구역을 생성할 수 있게 된다. wall-zone 연계의 경우 zone의 일부분을 DEM의 요소인 wall로 바꾸어 주는 방법이다. 압밀은 zone에 입력된 초기지중응력에 의해 압밀이 이루어지게 하였다. 이때, zone의 탄성계수를 적절히 선정해야 하는데, 만약 탄성계수가 너무 크면 wall-zone의 변위가 작아 입자에 응력이 충분히 전달되지 않으며, 탄성계수가 작을 경우 zone에 큰 변위가 발생하여 모델의 안정성이 떨어지게 된다. 본 논문에서는 삼축압축시험에서 도출된 탄성계수의 25%를 사용하였으며, TBM 굴진 전에 다시 원래의 탄성계수를 입력하였다. 최종적으로 wall-zone에 의한 압밀과정을 마친 후 모델의 모습이 Fig. 5에 나타나있다.
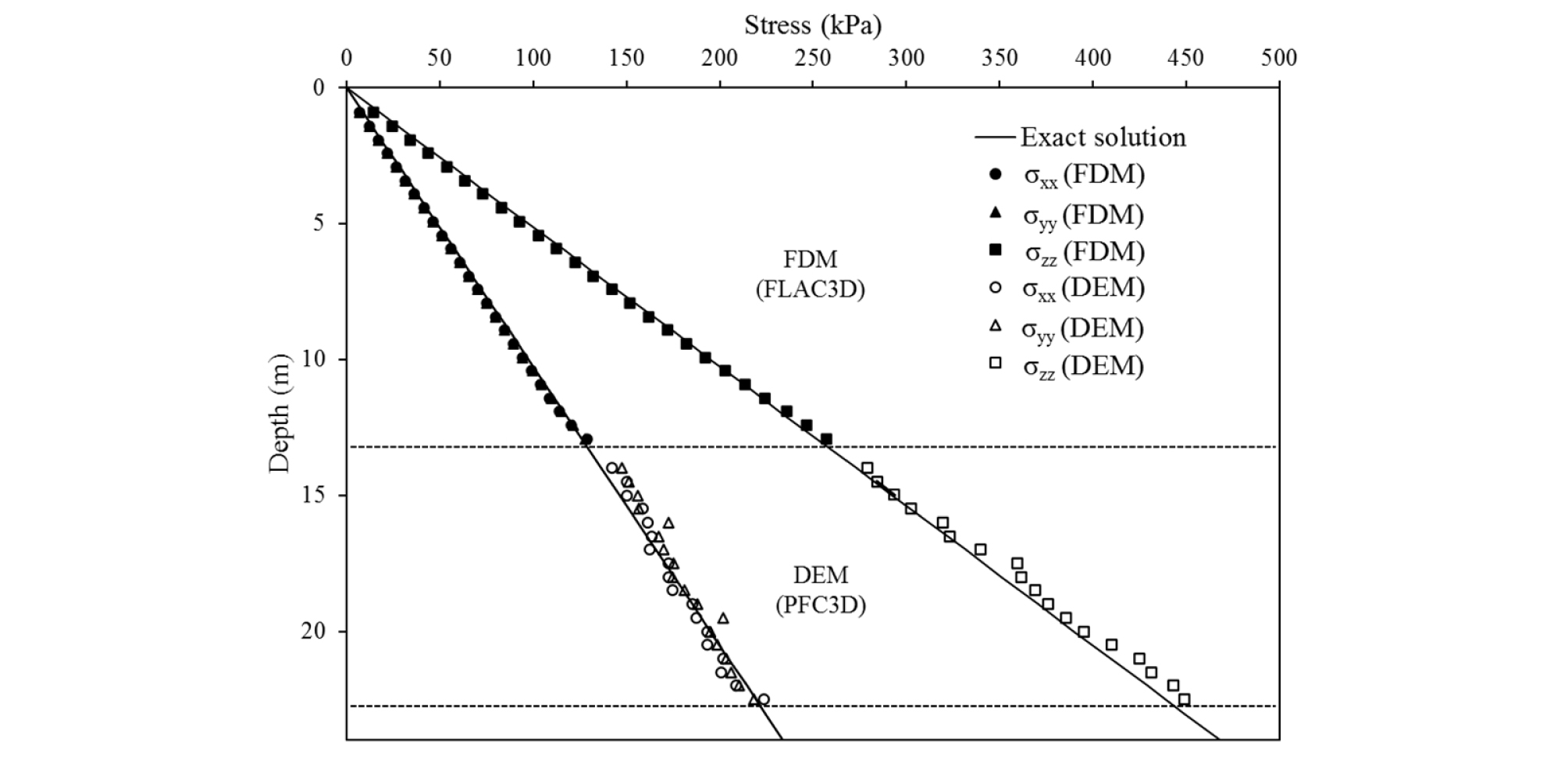
Fig. 6은 개별요소법-유한차분법 모델의 연계 검증을 위해 심도에 따라 수직 및 수평지중응력을 도시한 그래프이다. 유한차분법 구역의 경우 zone의 노드(node)를 통해 값을 도출하였으며, 개별요소법 구역의 경우 깊이 별로 측정구(measurement sphere)를 설치하여 지중응력을 산정하였다. 그림을 보면 개별요소법-유한차분법 경계를 포함한 수직 및 수평지중응력이 적절히 형성되어 있음을 확인할 수 있다.
3.3 지반모델 내 TBM 설치
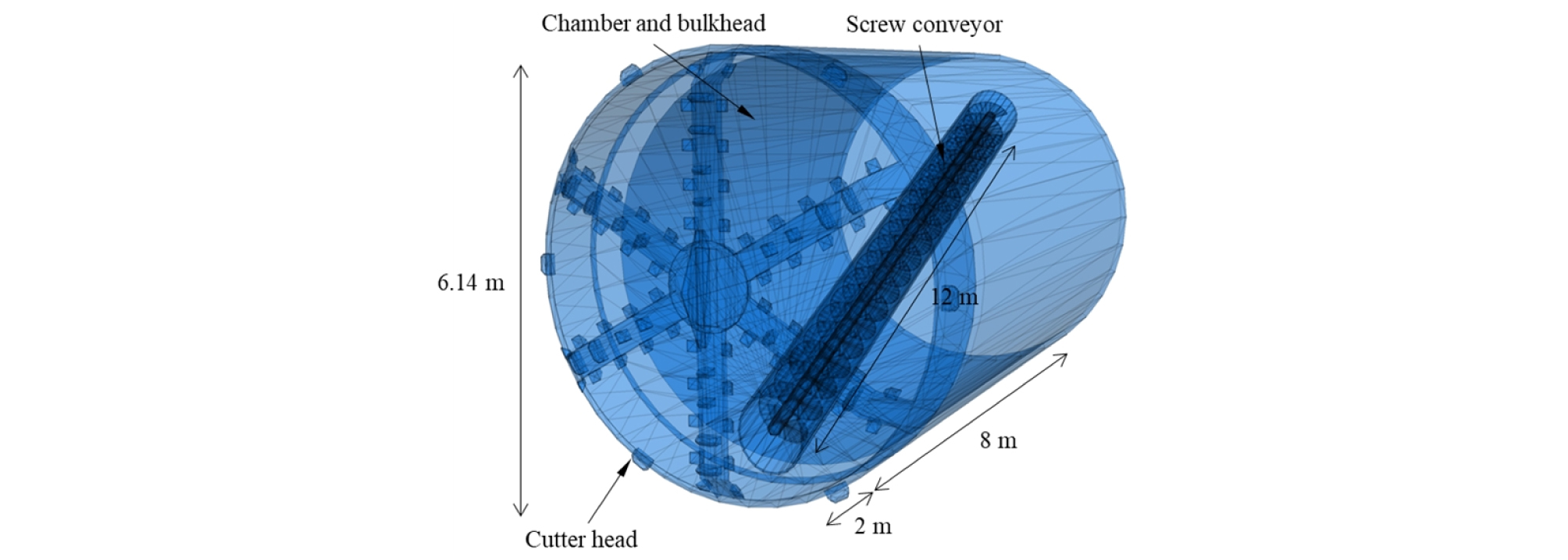
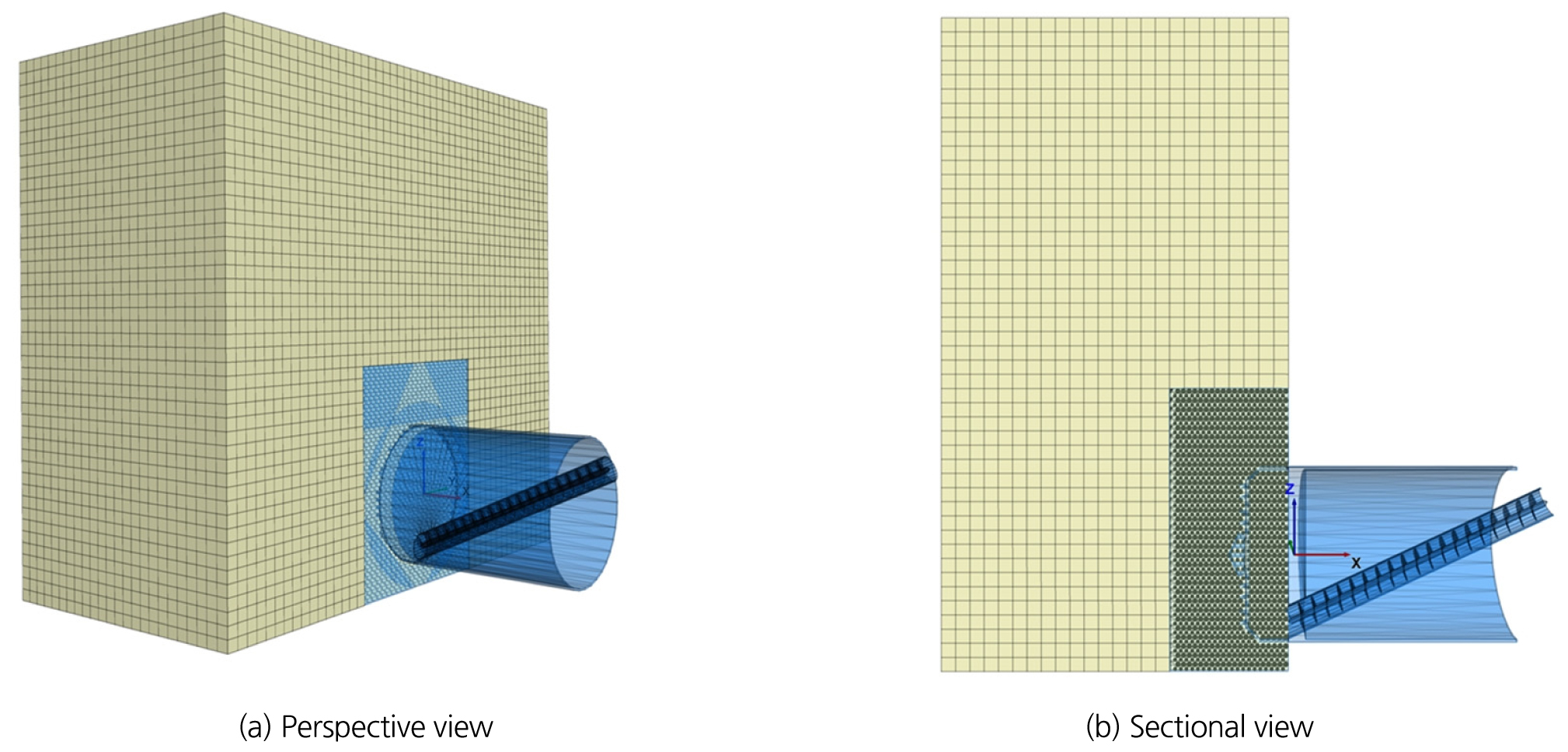
마지막으로 굴진 해석 모델링을 완료하기 위해서는 지반 내에 TBM을 설치해야 한다. 본 논문에서 적용된 TBM의 경우 EPB 쉴드 TBM으로 스포크 타입 TBM을 사용하였다. Fig. 7과 Table 2에 본 논문에서 사용된 TBM의 규격이 정리되어있다. 조성된 개별요소법-유한차분법 연계 지반모델에 TBM을 관입시킨 모습이 Fig. 8에 나타나있다. 이때, TBM은 피쉬테일 커터를 포함한 커터헤드 및 챔버 격벽 길이를 고려하여 총 2 m 관입하여 설치되었다. 챔버 내 공간은 초기 지중응력 상태의 ball로 채워 넣었다. 이는 굴진해석 시작 시 챔버가 비어 있거나 덜 채워져 있을 경우 지반을 구성하는 ball 입자들이 챔버 내로 급격히 쏟아져 내려 상부 침하가 크게 발생하기 때문이다. 침하가 과도하게 발생하면 개별요소법-유한차분법 경계의 ball과 wall-zone의 접촉이 이루어지지 않아 연계해석이 되지 않는다. 따라서 ball 요소와 TBM을 구성하는 wall 요소를 중첩되게 임포트하고, 중첩되는 ball 요소를 제거하는 코드를 작성하여 TBM의 설치를 완료하였다. wall과 중첩이 되어있는 ball이 생길 경우 해석 중 이상 응력이 발생하여 결과에 오류를 가져올 수 있다. 이를 위해 TBM의 모든 wall 요소는 폐합(closed)되어 있어야 한다. ball과 TBM wall의 상호 겹칩(overlap)을 제거한 모델의 절단면을 Fig. 8(b)에서 확인할 수 있다. 조성된 지반 내에 TBM 관입까지 완료되면 TBM의 특정 운전조건을 입력하여 해석을 수행한다.
Table 2.
Specification of EPB TBM for coupled DEM-FDM TBM driving model
4. EPB TBM 굴진해석 수행 및 결과
본 논문에서 제안한 모델에서는 굴진율, 커터헤드 및 스크류 컨베이어의 회전속도 세 가지의 운전조건을 조절할 수 있으며 토크, 추력, 챔버압, 배토량의 4 가지 TBM 운전데이터를 측정할 수 있다. 토크의 경우 해석 중 굴진 축(x축)을 기준으로 하여 굴착도구를 포함한 커터헤드 전체에 걸리는 토크 값을 읽는다. 추력의 경우에는 TBM wall 모든 요소의 굴진방향(-x 방항) 힘을 합쳐 구한다. 챔버압의 경우에는 격벽에 작용하는 힘을 면적으로 나누어 산정하였다. 마지막으로 배토량의 경우 스크류 컨베이어를 통해 배토되어 모델의 경계(domain) 밖으로 나가는 ball을 삭제하면서 삭제된 공의 개수를 이용하여 산정했다.
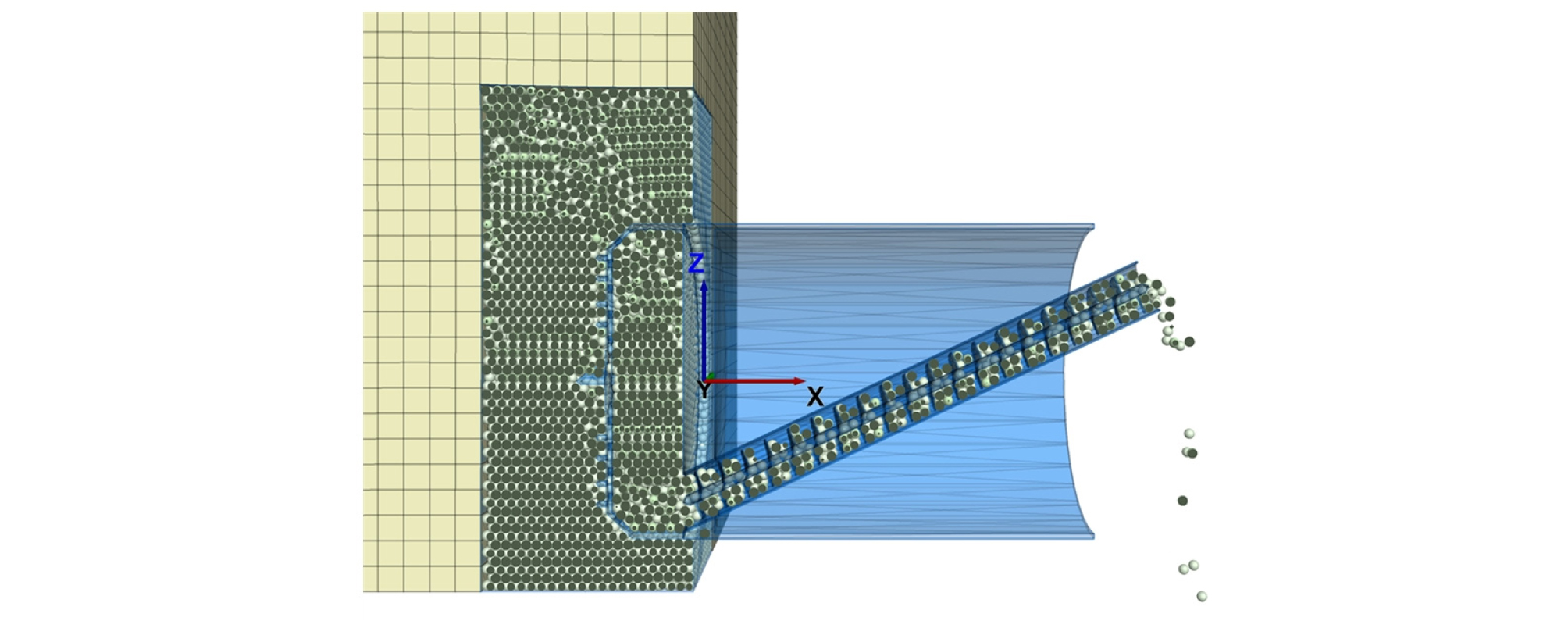
모델을 확인하기 위해 본 논문에서는 2 rpm의 커터헤드 회전속도, 0.5 mm/min의 굴진속도로 Prev(penetration per revolution)는 1.5 mm/rev로 설정하여 굴진해석을 수행하였다. 스크류 컨베이어의 회전속도는 일반적인 스크류 컨베이어 속도의 상한 값인 25 rpm을 채택하여 굴진해석을 수행하였다. 굴진해석은 수집되는 데이터가 안정화되는 20 cm까지 수행되었고, 총 해석시간은 400초이다. Fig. 9는 본 논문에서 굴진 해석 중 모델의 절단면을 보여준다. TBM 굴진과 커터헤드 회전 의해 굴착된 지반이 챔버, 스크류 컨베이어를 통해 모델의 경계 밖으로 나가는 모습을 보여준다.
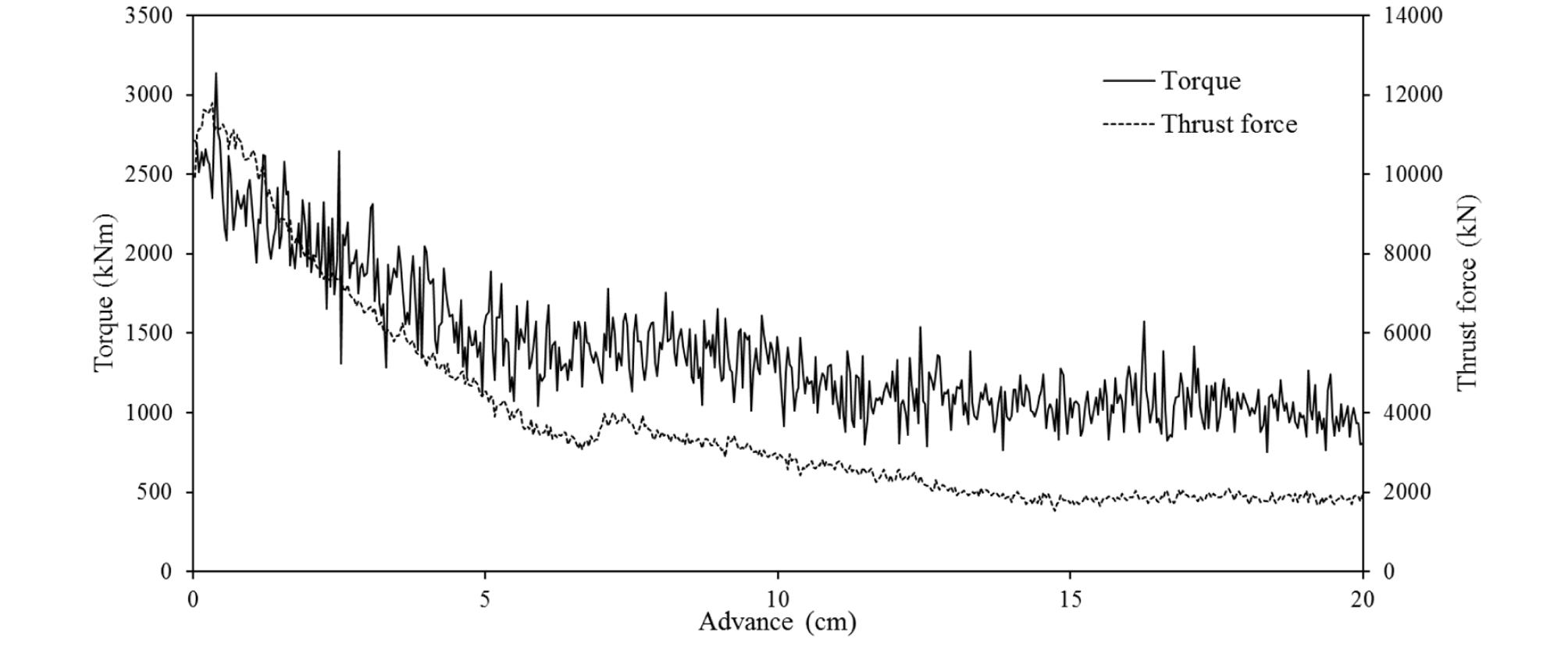
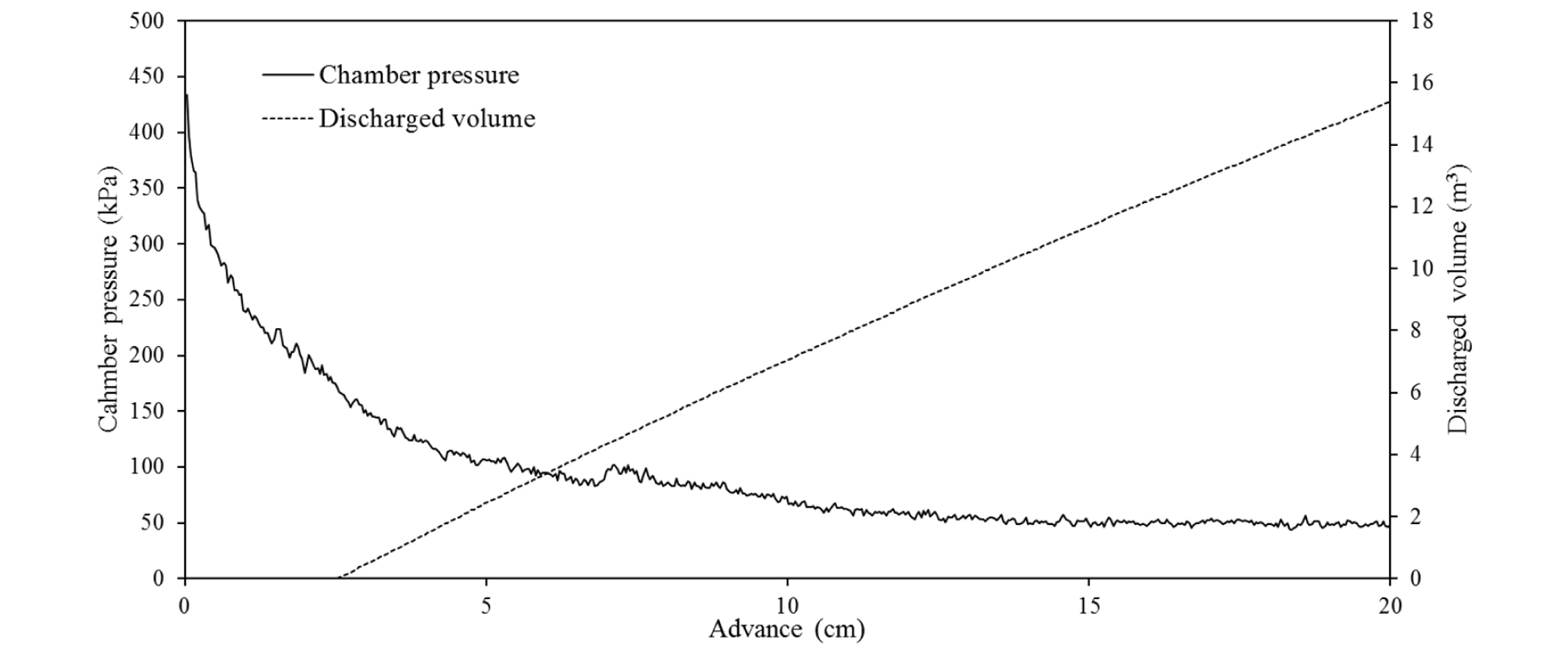
Fig. 10은 20 cm 굴진 중 측정된 토크와 추력 값을 나타낸다. 두 값 모두 10 cm 전・후 굴진까지 감소하다 특정 값으로 안정화 되는 경향을 나타냈다. 이는 해석 시작단계에서 개별요소법 구역의 급격한 침하를 막기 위해 지중응력 조건의 ball을 챔버 내에 가득 채웠기 때문이며, 스크류 컨베이어의 회전에 의해 배토가 되며 과다하게 걸린 토크와 추력이 해소된 것이다. 토크의 경우 평균 약 4,000 kNm의 값에서 수렴하였으며, 추력의 경우 2,000 kN의 수준에서 안정화 되었다. Fig. 11은 20 cm 굴진 중 측정된 챔버압과 배토량을 나타낸다. 챔버압의 경우 토크, 추력의 경우에서와 마찬가지로 10 cm 전・후 굴진까지 감소하다 특정 값으로 수렴하는 경향을 나타냈다. 이는 초기 챔버 내에 가득 찬 ball 요소들 때문이며, 스크류 컨베이어를 배출되는 입자에 의해 챔버압이 시간에 따라 소산된 것이다. 배토의 경우 약 2.5 cm (50초) 지점에서 발생하기 시작하였으며, 0.044 m3/sec의 배토속도를 나타냈다. 챔버압의 경우 평균 약 50 kPa의 값에서 수렴하였다. 전반적인 토크, 추력, 챔버압은 일반적으로 EPB TBM에 나타나는 하중보다 작게 나타났다. 이는 해당 운전 조건이 TBM 최적 굴진을 위한 굴진속도 보다 작거나 스크류 컨베이어의 회전속도가 과다한 조건임을 의미한다.
5. 결 론
본 논문에서는 기존 개별요소법 해석에서 ball 입자에 의해 이루어진 부분 일부를 유한차분법의 zone으로 대체하는 방법으로 개별요소법과 유한차분법을 연계한 EPB TBM의 굴진 수치해석 모델을 제시하였다. 본 논문의 결론은 다음과 같이 요약될 수 있다.
1) 제안된 모델의 경우 개별요소법 구역과 유한차분법 구역으로 나누어져 있으며 개별요소법 구역에 물성치를 적용할 때는 접촉모델 선정과 입자 접촉물성 검정과정이 필요하다. 본 논문에서는 일련의 삼축압축시험 모사를 통해 adhesive rolling resistance linear 접촉조건의 입자 접촉물성을 도출하고 모델에 적용하였다.
2) 개별요소법과 유한차분법을 함께 사용하여 지반을 모델링함으로서 개별요소법만을 사용하였을 경우에 비해 사용되는 입자의 개수를 크게 줄여 해석 효율을 크게 증가시켰으며, 추가적으로 수평응력계수를 고려한 지중응력을 모사할 수 있도록 하였다. 이때 연계 지반 모델링을 위해서는 wall에 의한 압밀과정과 wall-zone에 의한 압밀과정을 거쳐야 한다. 마지막으로 wall 요소로 이루어진 EPB TBM을 임포트 하여 모델링을 완성한다.
3) 모델의 해석 가능성을 검증하기 위해 2 rpm의 커터헤드 회전속도, 0.5 mm/min의 굴진속도, 25 rpm의 스크류 컨베이어 회전속도의 임의의 EPB TBM 운전 조건 하에 굴진해석을 수행하였고 이에 따른 토크, 추력, 챔버압, 배토량이 측정되는 것을 확인하였다. 측정된 데이터를 통해 해당 운전조건은 최적 운전조건에 미치지 못하며, 굴진속도를 증가시키거나 스크류 컨베이어 회전속도를 감소시켜야 한다.
4) 본 논문에서 제안된 모델을 바탕으로 향후 해석적 연구에서는 굴진속도, 스크류 컨베이어 회전속도 등의 운전조건를 변화시키며 토크, 추력, 챔버압, 배토량을 확인하여 운전조건에 따른 TBM 굴진성능을 평가하는 매개변수 해석 연구를 진행할 수 있을 것으로 판단된다.