1. 서 론
2. 암석블록 거동조건 분석
2.1 암석블록 거동조건 이론식 수립
2.2 3DEC 수치해석 분석
2.3 암반-블록 경계면 응력전달비율 회귀분석
3. 결과 분석
3.1 지체응력 및 절리강성 조건에 따른 암석블록 거동 예측
3.2 지체응력 및 암석블록 위치에 따른 암석블록 거동 예측
4. 결 론
1. 서 론
지하공동의 굴착 과정에서 암반 내 절리면의 기하학적 특성으로 인해 생성되는 암석블록의 거동 여부는 지하공동의 구조적 안정성 및 낙반 등 붕락사고와 직접적으로 연관되어 필수적으로 고려되어야 할 요소이다. 암석블록의 거동 안정성 분석을 위해 절리면의 기하학적 분포와 암석블록의 자중만을 고려한 강체 해석이 사용되어 왔으나(Goodman and Shi, 1985), 이는 대심도 환경에서의 상대적으로 높은 지체응력조건 및 이에 따른 큰 암반변형을 반영하기에 적합하지 않다. 암석블록의 거동 분석에 있어서 강체 해석이 가지는 단점을 보완하기 위해 지체응력 및 암반변형에 대한 이론적, 수치해석적 방법론을 적용한 다양한 암석블록의 거동 안정성 분석 연구들이 수행되었다. 암석블록의 이론적 거동을 절리압축강도와 절리면 거칠기, 지반응력에 따른 절리닫힘정도로 분석하는 연구가 수행되었으며(Yow and Goodman, 1987), 절리암반 내의 터널에 대한 암석블록의 거동을 개별요소법으로 분석하는 연구 역시 수행되었다(Moon and Chang, 1992). 이외에도 암석블록의 거동분석을 위해 다양한 수치해석적 연구가 수행되었으나(Nomikos et al., 2002; Hwang, 2006; Menendez-Diaz et al., 2009; Cho, 2016), 해당 연구들의 경우 암석블록의 거동 분석에 강체 해석을 사용하거나 특정한 암석블록 분포조건에 대한 사례연구에 그치고 있어 다양한 지하공동의 개발 현장에서 암석블록의 거동 안정성을 신속하고 정확하게 분석하기에는 미흡한 점이 많다. 다양한 현장조건에서 암석블록의 안정성을 정량적으로 분석하는 연구 역시 수행되었으나(Kang, 2017), 해당 연구는 단순한 2차원 암석블록을 대상으로 진행되어 상대적으로 복잡한 기하학적 구조를 가지는 3차원 암석블록의 안정성 분석에는 적합하지 않다.
이 연구에서는 지체응력을 고려한 3차원 암석블록의 정량적인 거동 안정성 분석이 어려운 기존 연구들의 단점을 개선하기 위해, 3차원 대심도 지하공동 조건에서 암석블록의 거동조건에 대한 이론적 계산결과와 수치해석 결과간의 오차를 정량적으로 분석하여 도출한 이론적 계산결과를 보정하였다. 암석블록 거동조건의 이론식 수립을 위해 Kirsch해를 활용하여 지하공동 주변 응력분포를 도출하였으며, 암반-블록 경계면에서의 Coulomb 전단강도식에 기초하여 암석블록의 거동조건을 결정하였다. 수치해석 분석은 3차원 개별요소법 소프트웨어인 3DEC을 활용하여 진행하였으며, 다양한 지체응력 및 절리물성 조건에서 암석블록이 거동조건을 만족하는 응력분포를 도출하였다. 이때 발생하는 이론식 계산결과와 3DEC 수치해석 결과간의 오차 발생 원인을 암반-블록 경계면에서 작용하는 유효응력의 차이로 가정하였으며, 이를 절리면의 수직-수평 방향의 응력전달비율(stress transmission ratio)로 정량화하여 회귀분석을 수행하였다. 마지막으로 도출한 회귀분석 결과를 활용하여 다양한 현장 지체응력 및 절리물성 조건 하에서 암석블록의 거동 안정성에 대한 정확하고 신속한 예측가능 여부를 검증하였다.
2. 암석블록 거동조건 분석
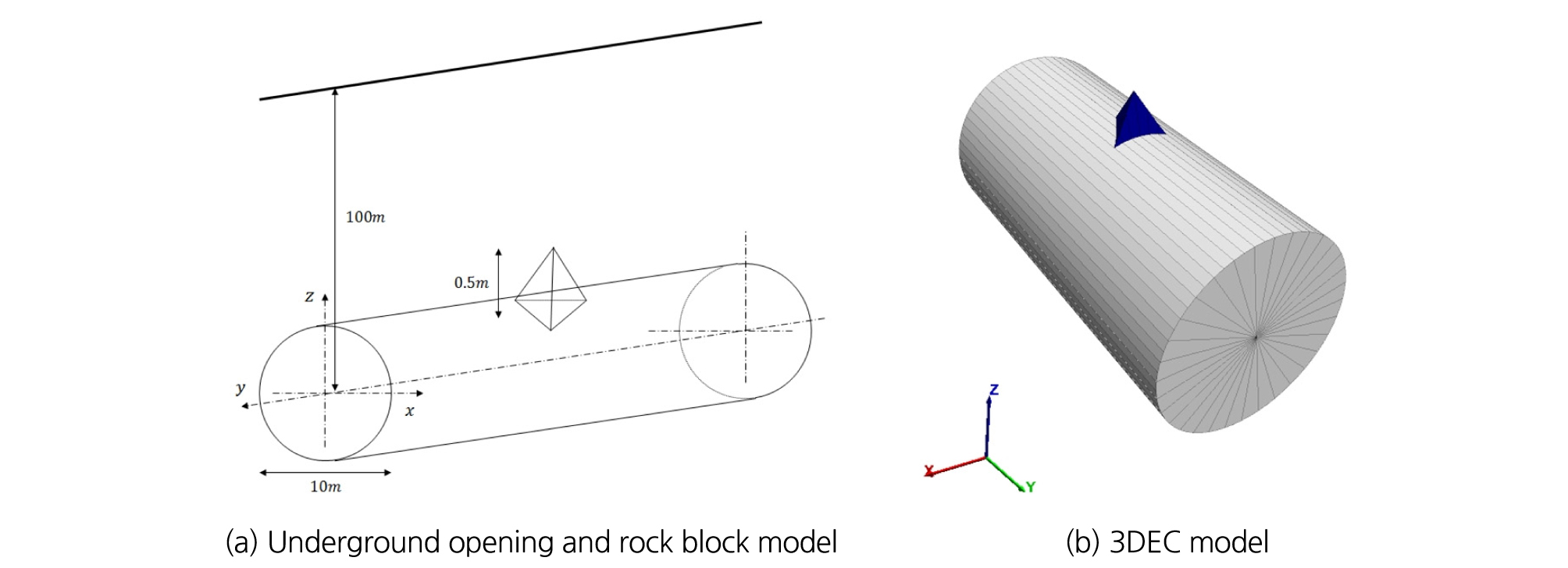
본 연구에서는 지체응력이 암석블록의 안정성에 유의미한 영향을 미칠 수 있는 대심도 환경에서의 3차원 지하공동 모델을 설정하였다. 본 연구에서 활용한 3차원 지하공동 모델은 Fig. 1(a)와 같이 심도 100 m에 위치한 직경 10 m의 원통형 터널이며, 3개의 서로 다른 절리면으로 이루어지는 높이 0.5 m의 정사면체 형태 암석블록을 터널 중심 천장부에 생성하였다. 이때 암반에 작용하는 수직응력성분은 심도에 따른 암반의 자중으로 결정하였으며, 수평응력성분은 수평/수직응력비율 조건을 만족하는 크기로 터널 굴착방향과 평행 및 수직한 방향에서 작용하였다. 3DEC 수치해석을 위한 3차원 지하공동 모델은 Fig. 1(b)와 같으며, 이때 암반의 물성조건은 아래 Table 1에 제시된 것과 같이 거창화강암의 물성조건을 활용하였다.
Table 1. Mechanical properties of rock mass used in this study (Kim, 2015)
| Material properties |
Unit weight (kN/m3) |
Young's modulus (GPa) |
Poission's ratio |
Tensile strength (MPa) | Friction angle (°) | Cohesion (MPa) |
| Property value | 25.9 | 44.0 | 0.23 | 6.2 | 51.3 | 14.0 |
2.1 암석블록 거동조건 이론식 수립
암석블록의 이론적 거동조건을 수립하기 위해 Coulomb의 전단강도식을 적용하였다. Coulomb식은 암반 절리면의 전단강도와 절리면에 작용하는 수직응력간의 관계를 선형적으로 나타낸 이론식으로, 응력이 작용하는 절리면의 거동을 간단하게 표현할 수 있다. 앞서 3개의 서로 다른 절리면을 통해 설정한 암석블록의 형태에 따라, 총 3개의 암반-블록 경계면에서 Coulomb식에 따른 전단조건을 동시에 분석하였다. 이때 암석블록의 거동조건은 최소 1개의 암반-블록 경계면에서 Coulomb 전단강도조건을 만족하지 못하는 경우로 결정하였다.
암반-블록 경계면에서 작용하는 응력성분의 경우, 원형 지하공동 주변의 응력해석을 위해 일반적으로 사용되는 Kirsch해를 적용하여 결정하였다. 지하공동 단면상에서의 응력분포는 암반에 작용하는 수직-수평응력 성분을 far-field 응력성분으로 설정하여 분석하였으며, 지하공동 단면과 수직한 방향의 응력성분은 암반에 작용하는 수평응력 성분과 동일한 값으로 설정하였다.
이와 같이 분석한 각 암반-블록 경계면에서 작용하는 응력성분을 Coulomb 전단강도식에 적용하여 암석블록의 거동조건 이론식을 안전율의 형태로 도출할 수 있으며, 이를 식으로 나타내면 아래 식 (1)과 같다.
식 (1)에서 σn,i, τi, Wn,i, Ws,i는 각각 암반-블록 경계면에서의 수직, 전단방향 응력성분 및 자중성분이며, ci, Ai, 𝜙i는 각 암반-블록 경계면의 점착력, 면적, 마찰각이다. 식 (1)의 분자 성분은 Coulomb 전단강도식에 따른 암반-블록 경계면의 전단강도이며, 분모 성분은 이론적으로 계산된 전단방향 응력성분의 크기이다. 이때 암석블록의 거동조건은 식 (1)을 통해 계산된 FoS값이 1 이하인 경우로 이론적으로 판단할 수 있다.
2.2 3DEC 수치해석 분석
앞서 수립한 암석블록 거동조건 이론식은 비교적 간단한 응력해석기법 및 절리면 거동해석기법을 적용하여, 지체응력의 작용에 따른 암반 및 절리면의 변형거동을 고려하는데 적합하지 않다. 따라서 본 연구에서는 3차원 개별요소 소프트웨어인 3DEC을 활용한 수치해석 결과를 암석블록 거동조건에 적용하여, 암반 및 절리면의 변형요소를 보다 정량적으로 표현할 수 있는 암석블록 거동 안정성 분석을 수행하였다. 이때 3DEC 수치해석 결과를 앞선 암석블록 거동조건 이론식에 보다 용이하게 적용하기 위해 분석대상 암석블록에 작용하는 가상의 힘인 인발력(Pulling force)을 설정하였다. 인발력은 암석블록 거동조건에 따라 FoS > 1 값을 가져 거동 안정성을 가지는 암석블록의 탈락을 유도하는 방향으로 작용하는 응력성분으로, 인발력의 크기 및 방향을 조절하여 암석블록이 거동하기 시작하는 임계조건(critical state)에서의 인발력 및 지체응력 조건을 도출할 경우, 해당 조건에서의 FoS값은 이론적으로 1로 수렴하게 된다. 아래 Table 2, 3은 3DEC 수치해석 분석 과정에서 활용한 절리면 물성조건을 나타내며, Table 4는 각 지체응력 및 물성조건에서 분석된 인발력 값을 나타낸다. Table 2에 제시된 절리면 물성조건의 경우 UDEC 및 3DEC 소프트웨어에서 제공되는 ‘Rock:Granite – fine grained’ 물성조건을 활용하였다.
Table 2. Mechanical properties of rock joints used in 3DEC simulation (Itasca, 2014)
| Material properties | Friction angle (°) | Cohesion (MPa) | Dilation (°) |
| Property value | 32.0 | 0.1 | 5.0 |
Table 3. Joint stiffness conditions used in 3DEC simulation
kn/ks ks | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
| 2.0 | 4.0 | 5.0 | 6.0 | 7.0 | 8.0 |
| 3.0 | 6.0 | 7.5 | 9.0 | 10.5 | 12.0 |
| 4.0 | 8.0 | 10.0 | 12.0 | 14.0 | 16.0 |
| 5.0 | 10.0 | 12.5 | 15.0 | 17.5 | 20.0 |
Table 4. Analysis results of critical state pulling force in 3DEC
Table 3,4 에 제시된 것과 같이, 본 연구에서는 일정한 암반 및 절리면 물성조건 하에서 지체응력의 측압계수 및 절리면 강성조건에 따른 암석블록의 거동조건을 3DEC 수치해석을 통해 분석하였다.
2.3 암반-블록 경계면 응력전달비율 회귀분석
앞서 2.2장에서 언급된 것과 같이, 2.1장에서 수립한 암석블록 거동조건 이론식은 암반 및 절리면의 변형거동을 반영하지 못한다는 단점이 있다. 따라서 본 연구에서는 3DEC 수치해석을 통해 도출한 임계조건에서의 인발력 값을 활용하여 이론적 거동조건을 보정하고자 하였다. 앞서 제시한 임계조건의 정의에 따라 Table 4 와 같이 분석된 인발력 값이 작용하는 경우, 식 (1)에서 도출되는 FoS값은 1로 수렴하게 된다. 따라서 이때 인발력 항을 포함한 식 (1)은 다음과 같이 표현될 수 있다.
식 (2)에서 Pn,i, Ps,i는 각 암반-블록 경계면에서 작용하는 수직, 전단방향 인발력 성분이다. 하지만 식 (2)에 응력성분 및 인발력 조건을 대입하여 계산할 경우, FoS값은 1로 수렴하지 않는 결과를 보이는 경우가 많다. 본 연구에서는 이와 같이 암석블록의 거동조건에서 이론식과 수치해석 결과간의 오차가 발생하는 원인으로, 각 암반-블록 경계면에서의 변형거동으로 인해 이론적으로 계산된 응력값과 실질적인 유효응력값 간에 차이가 존재할 것으로 가정하였다. 이를 보정하기 위해 본 연구에서는 식 (2)의 수직, 전단방향 응력성분에 대해 암반-블록 경계면에서의 이론응력 대비 유효응력 비율을 나타내는 응력전달비율(stress transmission ratio)을 추가하였다. 이때 식 (2)는 다음과 같이 표현된다.
식 (3)에서 rn, rs는 각각 수직, 전단방향의 응력전달비율을 나타낸다. 또한 이때 식 (3)을 응력전달비율에 대해 정리하면 다음과 같은 수직, 전단방향 응력전달비율의 1차식 형태로 식을 얻을 수 있다.
식 (4)와 같이 응력전달비율간의 1차식 형태로 식을 정리한 후, c1=c2=c3=c, A1=A2=A3=A, tan𝜙1 = tan𝜙2 = tan𝜙3 = α로 간소화하여 식 (5)와 같이 간단한 형태로 나타낼 수 있으며, 이를 식 (3)에 대입하여 식 (6)과 같이 임계조건에서 응력전달비율에 따른 암석블록의 거동조건을 FoS = 1 조건에 맞추어 도출할 수 있다.
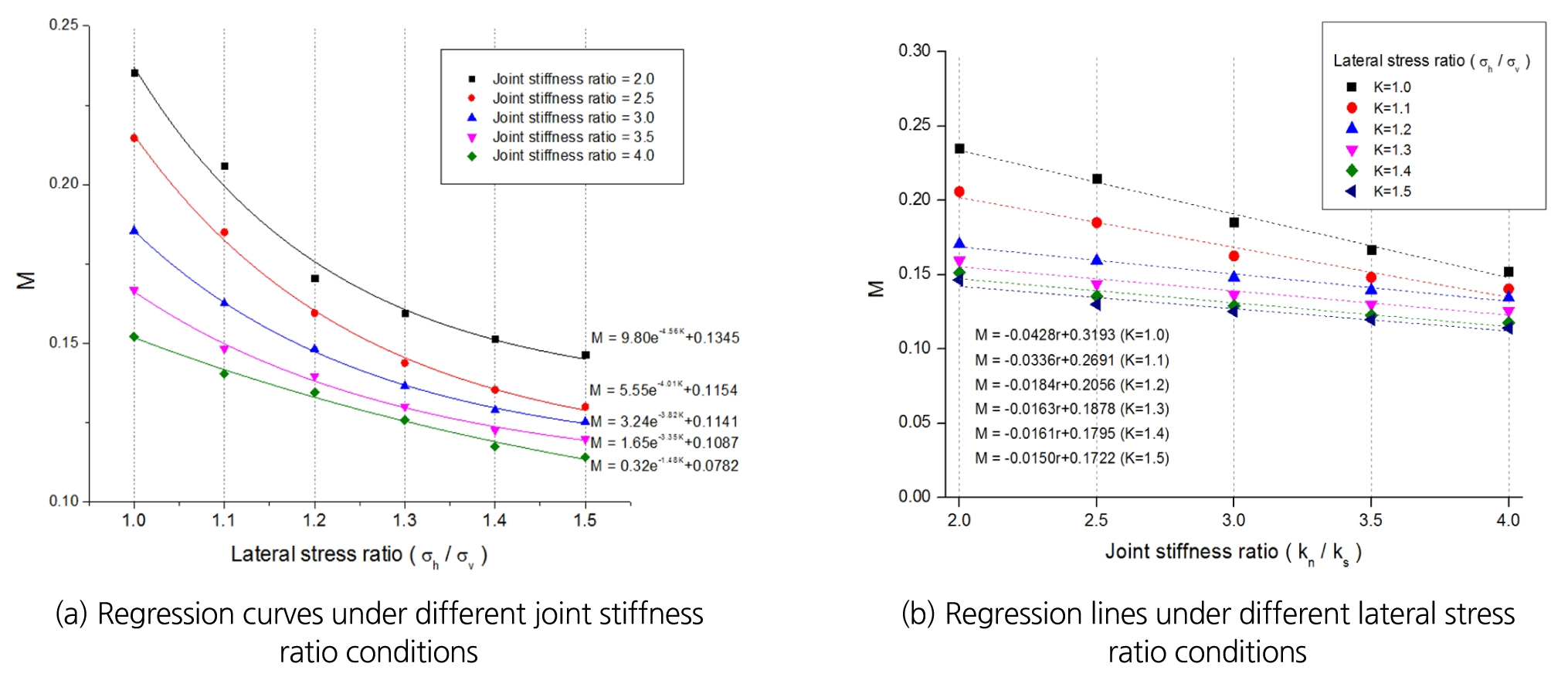
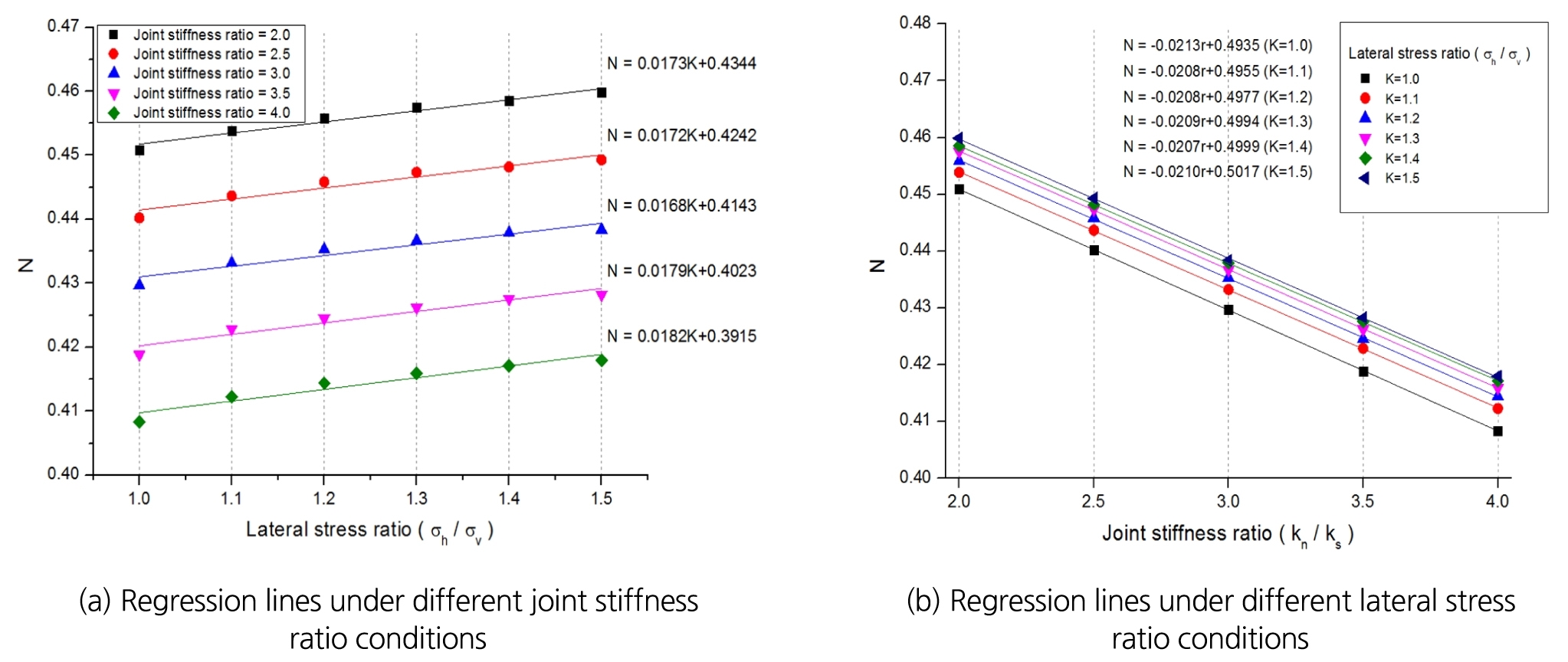
이때 식 (5)에서 나타나는 응력전달비율 rn, rs간 1차식의 계수 M, N은 이론적으로 도출한 암반-블록 경계면의 응력성분 및 3DEC 수치해석을 통한 임계조건 인발력, 암석블록의 기하학적 조건에 따라 계산할 수 있으므로, 지체응력 및 절리물성 조건에 따라 M, N을 정량화 가능하다면 식 (6)을 활용하여 rn, rs값 역시 정량적으로 계산이 가능하다. 따라서 본 연구에서는 M, N값의 정량화를 위해 다양한 지체응력 및 절리물성 조건 하에서 암석블록의 임계조건 인발력 값을 분석한 후, 이를 통해 계산되는 M, N값에 대한 회귀분석을 진행하였다. 분석 결과 암반에 작용하는 지체응력의 수평/수직응력비율(Lateral stress ratio, σh/σv) 및 절리강성비율(Joint stiffness ratio, kn/ks)에 따른 M, N의 회귀식을 도출하였다. 회귀분석 결과 및 도출된 회귀식은 아래 Fig. 2,3에 나타내었다.
3. 결과 분석
앞서 도출한 암석블록 거동조건 이론식 및 회귀분석 결과를 활용하여, 2장에서 활용한 것과는 다른 지체응력 및 절리물성을 적용해 실제 지하공동 개발 현장에서 현장자료를 활용한 암석블록의 거동분석 가능성을 검증하였다. 먼저 서로 다른 지체응력 및 절리강성 조건에 대한 분석을 진행하였으며, 암석블록의 위치에 따른 거동분석 역시 수행하였다.
3.1 지체응력 및 절리강성 조건에 따른 암석블록 거동 예측
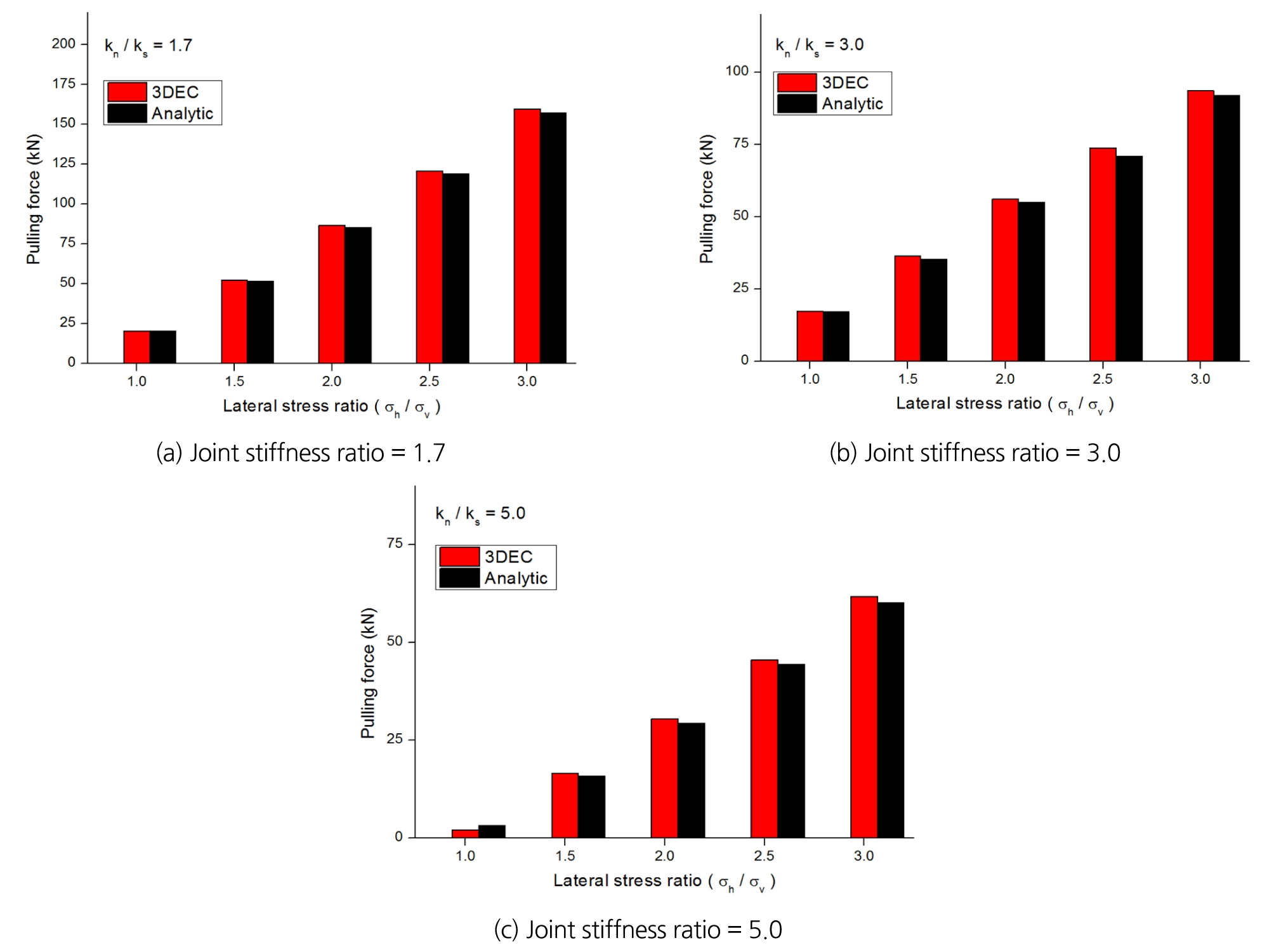
서로 다른 지체응력 및 절리강성 조건에 따라 암석블록의 거동 안정성을 분석하였다. 1.0-3.0 범위에서 0.5 간격으로 설정한 수평/수직응력비율 조건에서 수직절리강성이 10.0 GPa/m 일 때, 각각 1.7, 3.0, 5.0의 절리강성비율 조건 하에서 암석블록의 임계조건 인발력 값을 계산하였다. Fig. 4에 본 연구에서 제시한 암석블록 거동조건 이론식을 활용한 분석결과와 3DEC 수치해석 결과를 나타내었다. 수치해석 결과와 이론식간의 최대오차는 2.91 kN, 최대오차비율은 4.68%로 분석되었으며, 본 연구에서 제시한 이론식이 암석블록의 안정성을 일관적으로 저평가함을 확인할 수 있다.
3.2 지체응력 및 암석블록 위치에 따른 암석블록 거동 예측
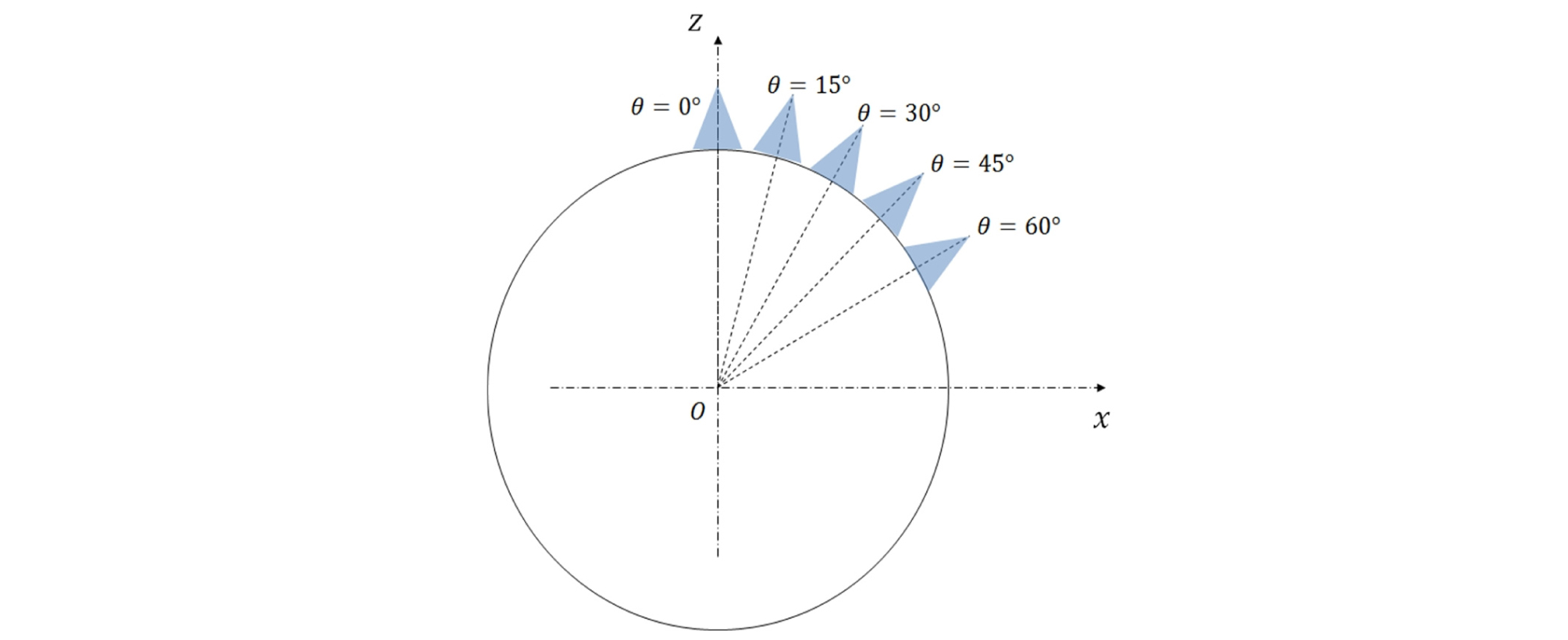
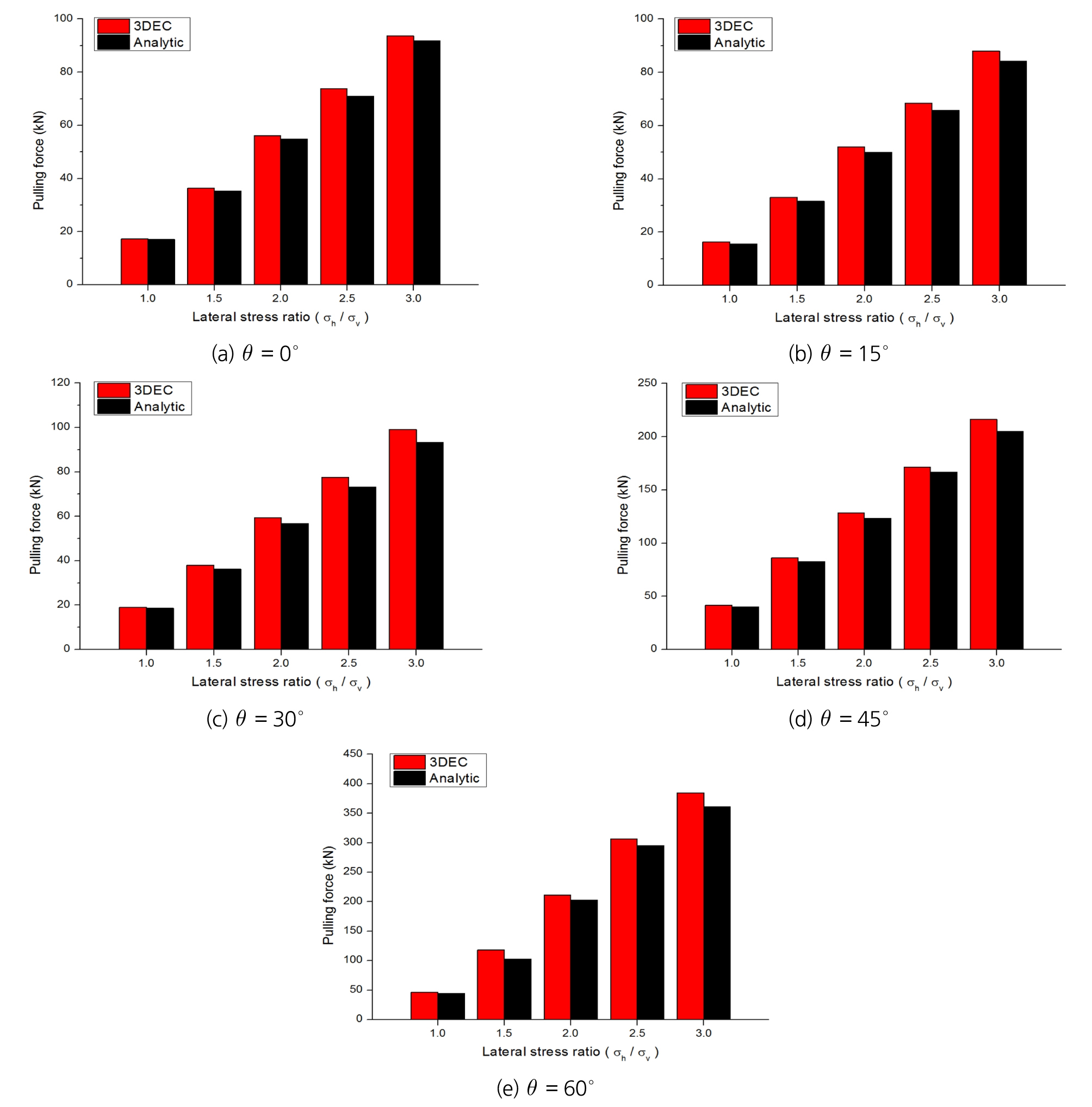
지하공동 주변부의 서로 다른 위치에서 암석블록의 거동 안정성을 분석하였다. Fig. 5와 같이 지하공동의 단면을 나타냈을 때, 지하공동 천장부를 기준점(θ = 0°)으로 60° 범위 내에서 15° 간격으로 암석블록이 위치할 때 암석블록 거동조건 이론식의 정확도를 분석하였다. 분석 과정에서 수평/수직응력비율 조건은 3.1절과 동일한 범위로 설정하였으며, 절리강성조건은 수직절리강성 10.0 GPa/m에 절리강성비율 3.0 조건으로 설정하였다. Fig. 6에 암석블록 위치에 따른 이론식 검증결과를 제시하였다. 앞선 3.1절의 검증결과와 마찬가지로 이론식 적용 시 암석블록의 안정성에 대한 과소평가가 관측되었으며, 이때 최대오차는 23.541 kN, 최대오차비율은 6.12%로 분석되었다.
4. 결 론
본 연구에서는 지체응력 및 절리물성의 영향을 고려할 수 있는 암석블록의 거동조건 이론식을 도출하였다. 이는 기존 암석블록의 거동해석기법이 강체해석 또는 특정한 상황에서의 암석블록 거동해석만을 모사하여 현장에서의 활용도가 제한적이었던 것과는 달리, 이론적 방법론과 수치해석기법을 접목하여 각 지체응력조건 및 절리물성조건에 따른 암석블록의 거동조건을 회귀적으로 분석하여 다양한 현장조건에서도 암석블록의 거동 안정성 분석이 가능함을 확인하였다. 또한 도출한 암석블록 거동조건 이론식을 회귀분석에 사용된 것과는 다른 지체응력 및 절리물성 조건에 대해 검증한 결과, 3DEC 수치해석을 활용한 분석결과와 비교하여 약 5% 미만의 오차범위 내에서 암석블록의 거동양상을 예측하여 분석결과의 정확성이 높은 것으로 판단되었다. 암석블록의 다양한 기하학적 위치에 따른 검증결과 역시 약 6% 이내의 작은 오차수준을 보였다. 비록 본 연구에서 제시한 암석블록의 거동분석 기법이 대상 암석블록의 안정성을 일관적으로 저평가하는 경향성을 보였으나, 이는 검증결과에서 도출된 5-6%대의 작은 오차수준을 고려할 때 현장 조사 자료가 가지는 부정확성을 보완하기 위한 지하공동의 안정적 설계기준으로 활용될 수 있을 것으로 여겨진다.
본 연구에서는 기초적인 응력분포분석 및 전단거동분석 기법인 Kirsch해 및 Coulomb 전단강도식만을 활용하여 연구를 진행하였다. 추후 불연속 암반의 응력분포분석 및 절리면의 거칠기 및 수리적 특성을 반영할 수 있는 전단거동식을 활용한다면 보다 정확하고 범용적인 암석블록의 거동분석이 가능할 것으로 생각된다. 또한 본 연구의 수치해석 과정에서는 3차원 개별요소 소프트웨어인 3DEC만을 사용하였는데, PFC3D 등 다양한 수치해석 소프트웨어를 활용한 본 연구결과의 검증 역시 암석블록의 거동분석에 대한 추가적인 연구로써 활용될 수 있을 것이다.