1. 서 론
2. 지류론에 의한 수직응력
3. FLAC3D 수치해석
3.1 메쉬 크기 설정 및 지류론 해석 정확도 검증
3.2 개발 심도에 따른 지류론 해석 정확도 검증
3.3 주방식 광산의 패널광주 수직응력 평가
4. 수치해석 결과 분석
5. 결 론
1. 서 론
토목 또는 건축 분야에서 설계 및 시공되는 건물 또는 교량 등의 구조물에서는 부재의 물성이나 구조가 명확하므로 구조물 거동을 비교적 정확하게 예측하여 관리할 수 있다. 그러나 광업 분야에서 암반 구조물을 설계 및 시공하는 경우에는, 암반을 구성하는 다양한 암층별 입자 구성이나 결합 조직의 편차로 인해 물성이 일정하지 않으며, 암반에 내재된 불연속면의 정확한 구조 파악이 어려우므로 다양한 가설을 적용하여 나날이 심부화되고 있는 악조건 속에서 암반 구조물의 거동을 예측하여 충분한 안정성을 확보하여야 한다(Jang and Lee, 2017, Yoon and Song, 2019). 국내외에서 지하광산 개발 시 주로 이용되고 있는 주방식 채광법에서는 암반 굴착 시에 암반 일부분을 의도적으로 남겨두어 패널 광주(pannel pillar)를 형성하고 이를 통해 상부 암반의 하중을 지지한다. 이때 광주에 작용하는 수직하중은 지류론(TAT, Tributary area theory)을 적용하여 계산하는 것이 일반적이며, 지류론에 의해 추정된 응력 수준을 고려하여 지하구조물의 설계 및 안정성 평가가 이루어지고 있다(Esterhuizen et al., 2012, Kim et al., 2012, Chang et al., 2014, Ghasemi et al., 2014, Kim, 2015, Jang, 2018). 지류론 추정법은 광주에 작용하는 수직응력을 신속하게 계산할 수 있다는 장점이 있으나, 응력 수준이 과대평가되어 광산 개발 경제성이 저하되는 단점이 있는 것으로 알려져 있다. 이를 보완하기 위해 응력 아치 연구(Poulsen, 2010), 수치해석 연구(Hauquin et al., 2016) 등의 선행 연구가 수행된 바 있으나 아직까지 적용성이 부족하고 검증이 불충분하므로 이에 대한 추가 연구가 필요하다. 본 논문은 광산 개발 경제성 제고를 위해 지류론의 단점을 보완하고 광주의 수직응력 평가 정확도를 향상시킴으로써 지하광산 갱도설계 최적화 기술을 개발하는 것을 목적으로 하였다. 이에 주방식 채광장을 모델링하여 광주에 작용하는 수직응력에 대한 3차원 전산해석을 수행하고 결과를 분석하였다.
2. 지류론에 의한 수직응력
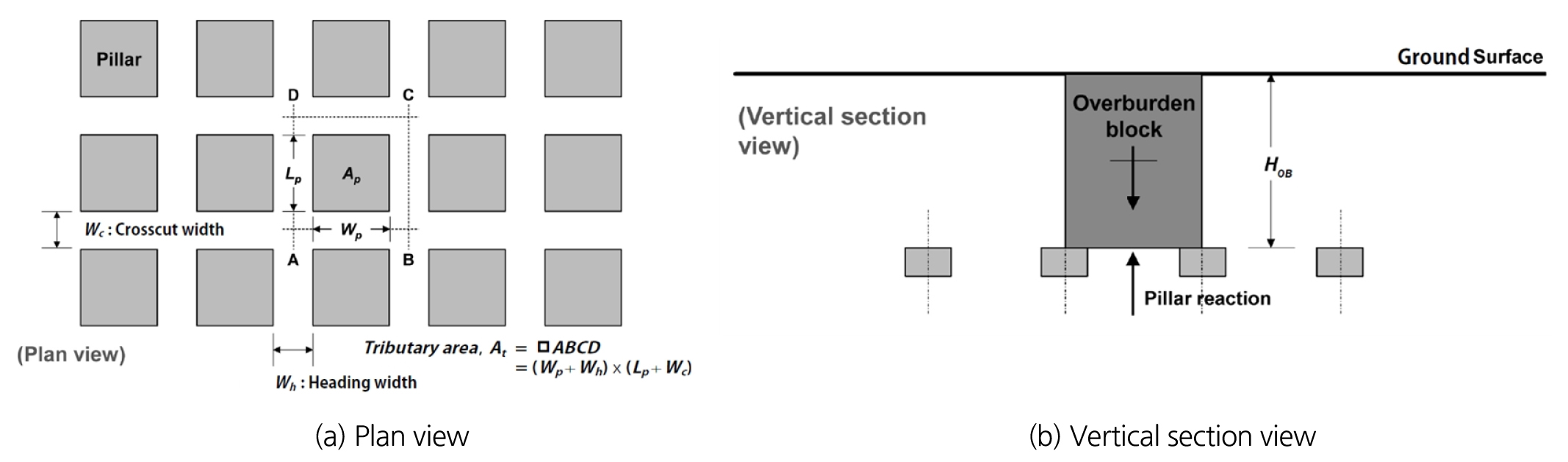
지하광산 개발을 위한 광주 및 채광장 설계 시 채광법, 채광 장비, 작업 효율, 경제성 등을 고려하여 헤딩과 크로스컷 너비 등의 채광장 규격을 설정하고, 채광장 굴착에 따라 광주에 집중되는 상부암반의 하중을 안정적으로 지지할 수 있는 광주 규격을 설정하여야 한다. 이때 광주에 작용하는 수직응력을 추정하기 위하여 Fig. 1과 같은 지류론 방식이 주로 사용되고 있다.
지류론 설계에서는 암반 내 채광장 굴착에 의하여 암반에 변형이 발생할 때 수평 변위가 구속되어 주방식 채광 영역의 상부 암반 자체하중이 모든 패널 광주에 동일하게 분배되는 것으로 간주하므로 식 (1)~식 (3)과 같이 해당 심도에서의 수직방향 현지응력에 지류론 하중면적과 광주의 면적비를 곱하여 수직응력을 계산한다(Chang et al., 2014).
| $$\sigma_{vi}=\gamma\times H_{OB}$$ | (1) |
| $$A_T=(W_P+W_H)\times(L_P+W_C)$$ | (2) |
| $$\sigma_P=\sigma_{vi}\times\frac{A_T}{A_P}$$ | (3) |
식 (1)에서 σvi는 상부 암반의 하중에 의해 추정되는 수직방향 현지응력(in-situ stress in the vertical direction), γ는 암반의 비중량(specific weight), HOB는 개발 심도(development depth)에 의해 결정되는 상부 암반 두께(height of overburden)를 의미하며, 식 (2)에서 AT는 지류론 하중 면적, WP는 광주 너비, WH는 헤딩(heading, 굴진 방향과 평행한 갱도) 너비, LP는 광주 길이, WC는 크로스컷(crosscut, 굴진 방향과 직교하는 갱도) 너비를 의미하고, 식 (3)에서 AP는 광주 단면적을 의미한다. 지류론 설계는 패널 광주에 작용하는 수직응력을 신속하게 예측할 수 있다는 장점이 있으나 실제 암반에서는 채광장 굴착으로 인해 암반이 변형될 때 수직 방향뿐만 아니라 수평 방향으로도 변위가 발생하며 채광장을 둘러싼 암반에 의한 지지효과가 더해지기 때문에 상부 암반의 모든 하중이 광주에 작용한다고 보기 어려우며, 천정부 처짐에 의한 모멘트 하중과 암반의 아칭효과 등을 고려하지 않으므로 수직응력 예측 정확도가 저하되는 단점이 있다. 횡방향 규모가 충분히 크고 개발 심도가 얕은 경우에는 지류론 방법으로 수직응력을 추정하는 것이 유리할 수 있으나, 일반적인 경우에는 수직응력이 과대평가되어 광산 개발 경제성을 저해하는 것으로 평가된다. 이 연구에서는 주방식 채광장을 3차원 모델링하여 채광장의 개발 심도, 개발 규모에 따른 패널 광주의 수직응력 변화를 추적 관찰함으로써 지류론 방식의 수직응력 추정 방법을 보완하고 암반 거동에 대한 이해를 넓히고자 하였다.
3. FLAC3D 수치해석
3.1 메쉬 크기 설정 및 지류론 해석 정확도 검증
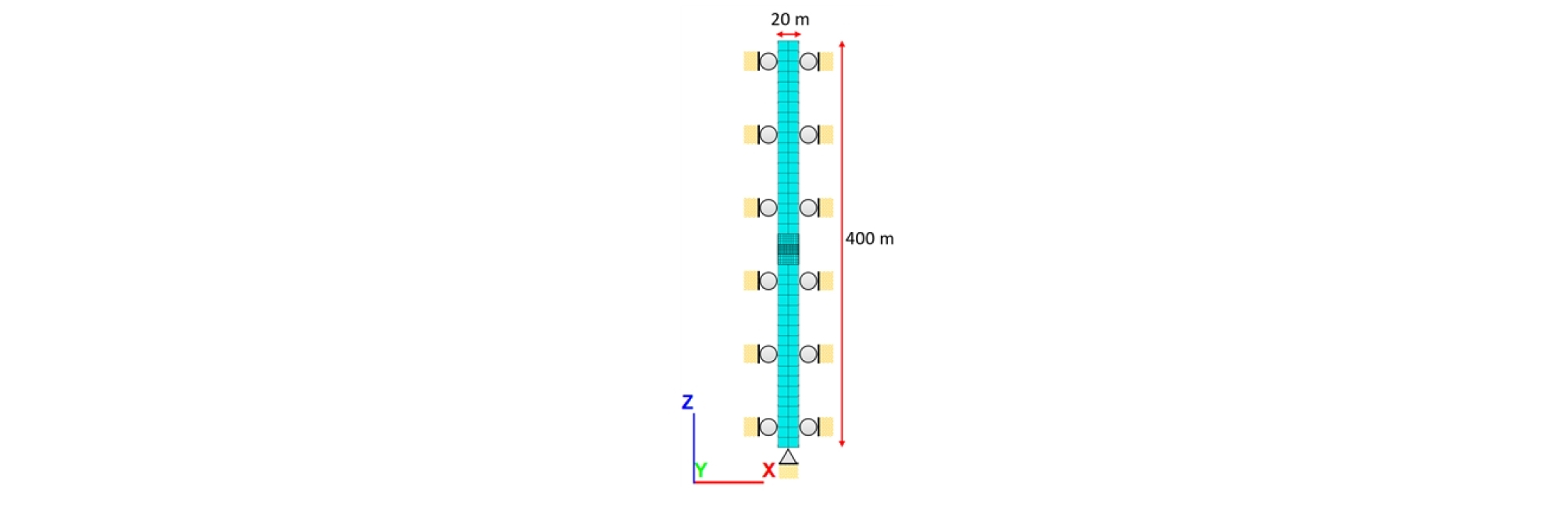
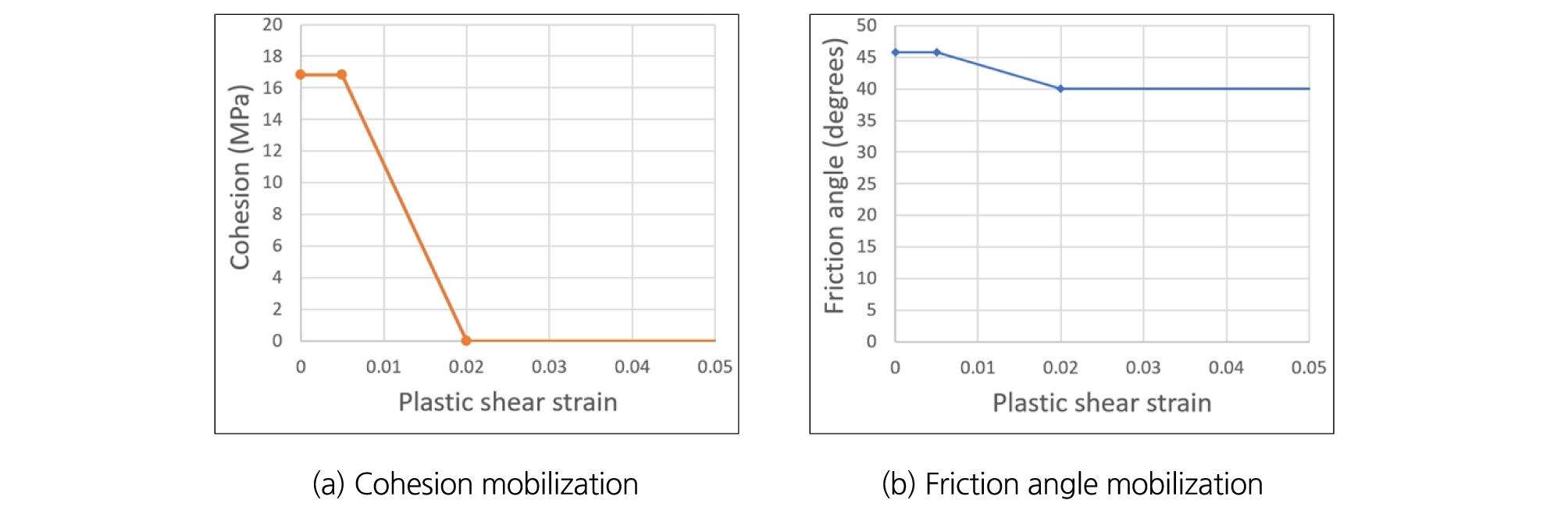
3차원 수치해석을 수행하는 경우 2차원 해석에 비해 암반 거동을 높은 정확도로 모사할 수 있으나, 해석시간이 오래 소요되므로 다수의 사례를 해석하는 데에는 다소 불리하다. 따라서 본 모델의 해석 수행에 앞서, 수치해석 정확도와 소요시간을 최적화하기 위해 적절한 요소망(mesh) 크기를 설정하고 수치해석 소프트웨어의 해석 성능을 검증하고자 하였다. 3차원 유한차분법 프로그램인 FLAC3D을 사용하여 Fig. 2와 같이 가로×세로×높이가 20 m×20 m×400 m인 연속체 암반을 생성하고 메쉬 형상(shape)을 육면체 요소(brick element)로 설정하였다. 경계조건 설정을 위해 X방향과 Y방향으로 변형이 발생하지 않도록 수평 방향으로의 변위를 모두 구속하였으며, 모델 바닥면에서 Z방향 변위 발생을 제한하였다. 구성방정식을 변형률-연화(strain-softening) 모델로 설정하고 Fig. 3(a), (b)와 같이 전단 소성변형률이 0.5%를 초과하여 2%에 도달할 때까지 점착력은 전부 소실되고, 마찰각은 5°감소하도록 설정하여 해석을 수행하였다. 암반 물성은 균질 등방성 재료의 탄성계수 변환식인 식 (4), 식 (5)을 이용해 암반 물성 설곗값인 탄성계수(E) 43.5 MPa, 포아송비(υ) 0.2를 만족하는 체적탄성계수(K) 및 전단탄성계수(G) 값을 역산하여 입력값으로 사용하였다. 모델에 적용된 물성값은 Table 1과 같다.
| $$K=\frac E{3(1-2\nu)}$$ | (4) |
| $$G=\frac E{2(1+\nu)}$$ | (5) |
Table 1.
Mechanical properties of the verification model
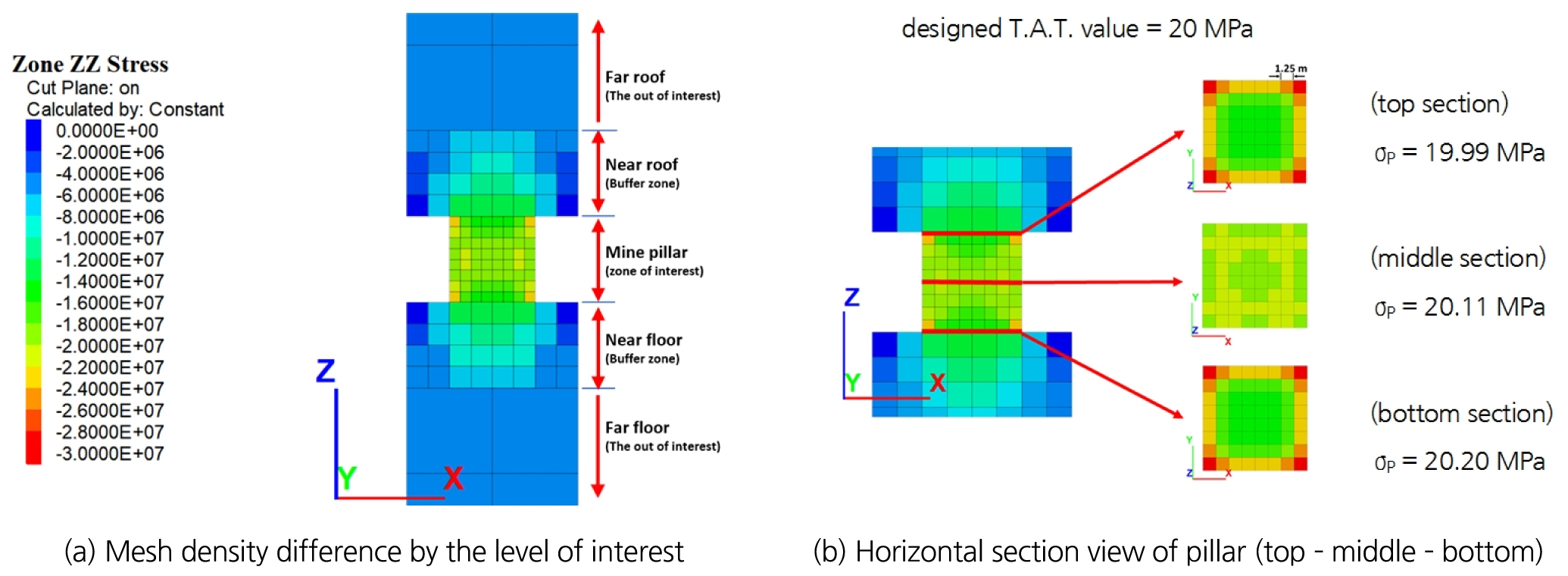
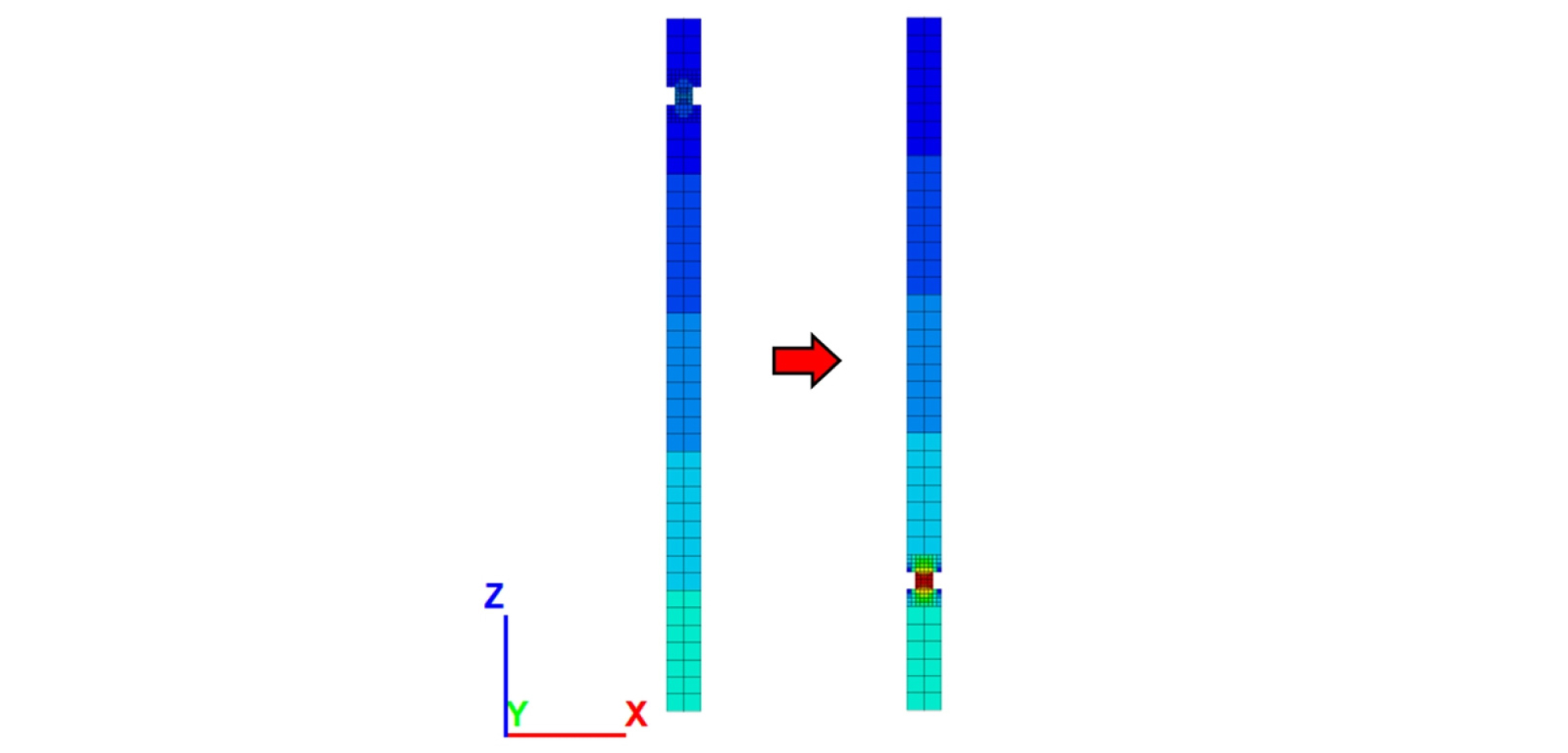
수치해석 결괏값 분석의 편의를 위해 암반 밀도(ρ)를 2,500 kg/m3, 중력가속도(g)를 10m/s2으로 설정하고, 측압계수(k)는 0.5로 설정하여 안정화(equilibrium) 과정을 수행하였다. 이후 심도 200 m지점에서 채수율(e, extraction ratio)이 75%가 되도록 채광장과 광주 너비를 동일하게 설정하여 공동을 굴착하여 너비×길이×높이가 10 m×10 m×10 m인 정방형 광주를 생성하였으며, FLAC3D의 수렴(convergence) 기본 설정을 이용하여 평균 불균형력 비(average force ratio)가 1E-5 미만에 도달할 때까지 해석을 진행하였다. 지류론에 의한 수직응력 설곗값은 20 MPa이며, Fig. 4(b)와 같이 광주 최상단, 중단, 최하단의 요소군에서 평균 수직응력을 측정한 결과 각각 19.99 MPa, 20.11 MPa, 20.20 MPa로, 상부 암반과 접해 있는 최상단 요소군에서 지류론 계산값과 가장 근사한 수치를 보였다. 지류론에서는 광주 자체 하중의 영향은 고려하지 않으며, 광주가 상부 암반의 하중과 하부 암반의 반력에 의한 일축압축상태인 것으로 간주한다. 따라서, 해석 시에 수직응력 값을 광주 최상단 요소군에서의 수직응력 평균값으로 결정하여도 무방한 것으로 판단하였다.
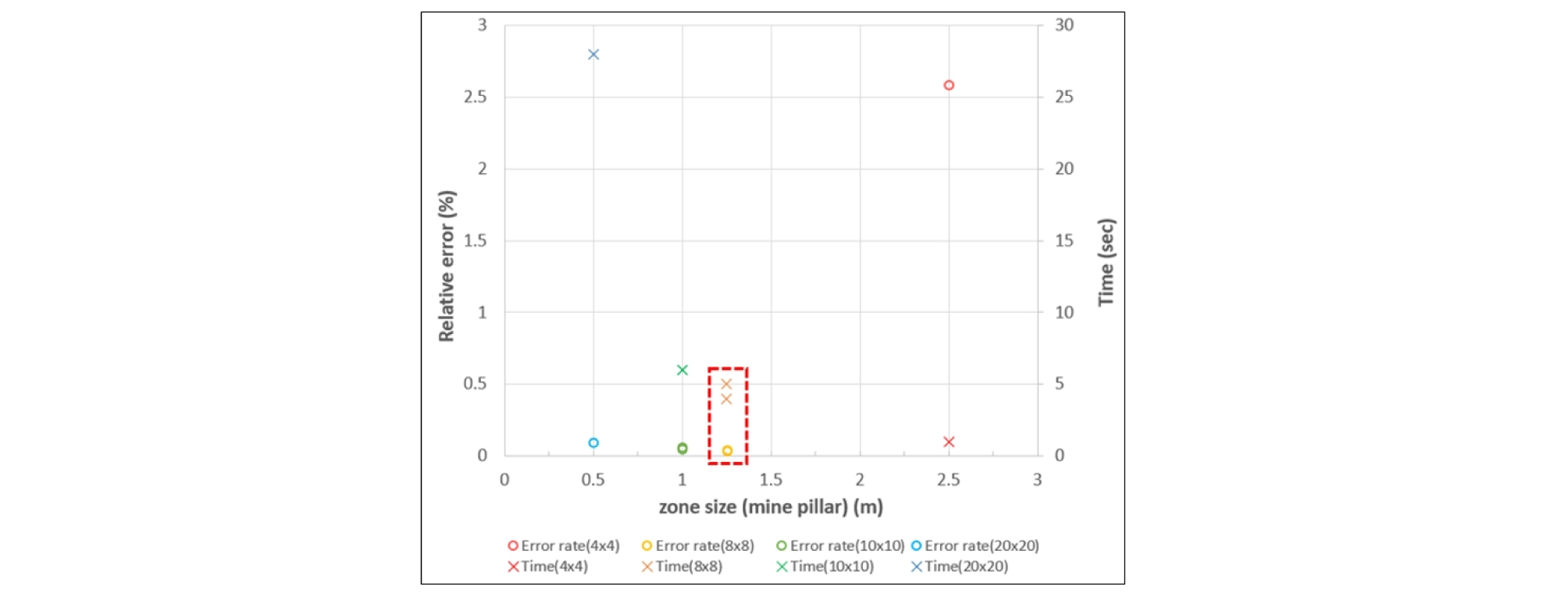
이와 동시에 Fig. 4(a)와 같이 검증 모델을 원거리 천정 및 바닥부(관심 외 영역), 근거리 천정 및 바닥부(완충 영역), 광주부(관심 영역)으로 구분하고, Table 2와 같이 관심 외 영역 - 완충 영역 - 관심 영역 순으로 메쉬가 조밀해지도록 구성할 수 있는 여러 메쉬 조합을 검토하여 모델 해석 시 오차 발생을 최소화하고 해석 성능을 최적화할 수 있는 조합을 탐색하였다. 이때 관심 외 영역의 요소 크기는 10 m로 고정 적용하였다. Fig. 5는 메쉬 크기 조합별 상대오차와 소요시간에 대해 분석 결과이며, 광주 수평단면에 8×8 개의 요소가 포함되도록 모델 요소 크기를 조합하는 경우에 정확도와 신속도가 가장 우수한 것으로 분석되었다. 이용 가능한 두 가지 조합 중 완충 영역의 해상도가 더 높은 Case-B 조합을 선정하여 모델에 적용함으로써 광주에 접해 있는 근거리 천정 및 바닥부의 암반 거동을 함께 관찰하고자 하였다.
Table 2.
Combinations of mesh sizes and performances
3.2 개발 심도에 따른 지류론 해석 정확도 검증
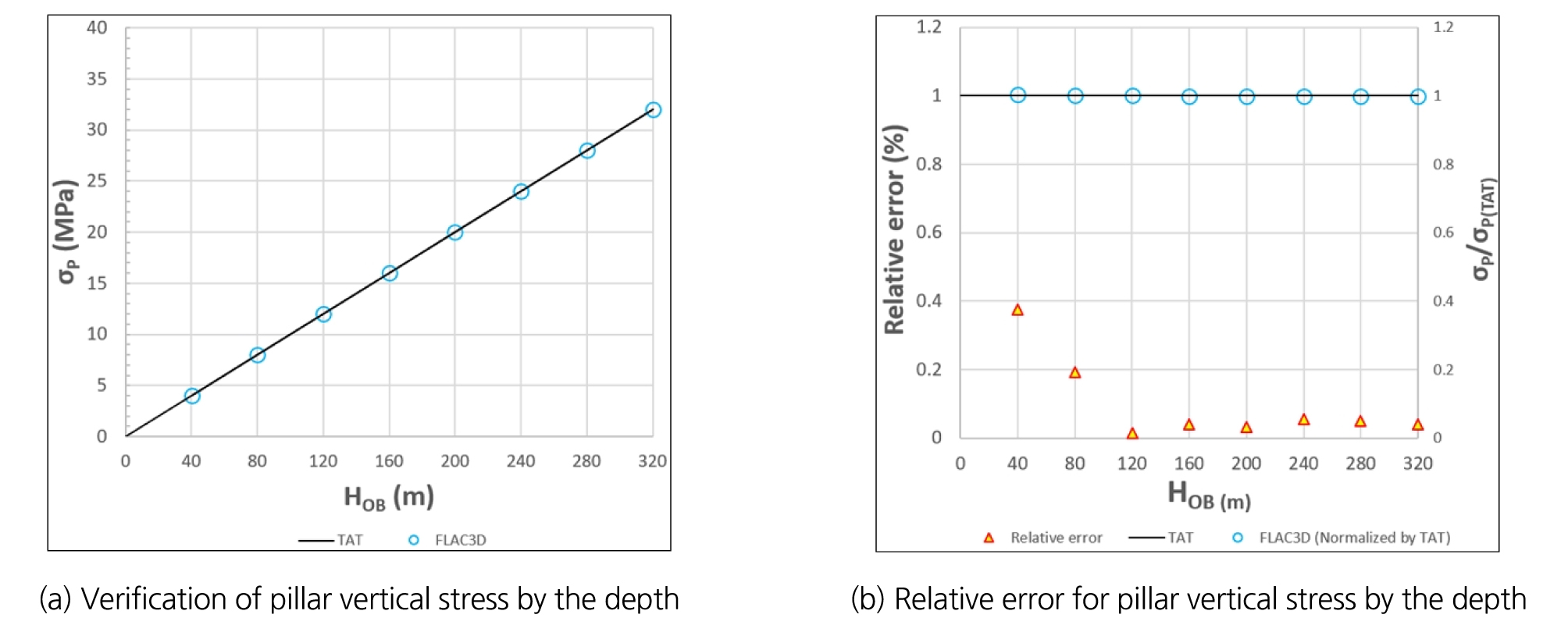
Case-B의 조합을 적용하여 이전과 동일한 크기의 암반 모델을 생성하고 Fig. 6과 같이 40 m~320 m까지 40 m 단위로 굴착심도를 변경하면서 광주 상부에 작용하는 수직응력을 측정하여 심도에 따른 지류론 해석 정확도를 평가하였다. Fig. 7(a), (b)는 심도별 해석 성능평가 결과이다. 가장 얕은 40 m 심도에서 가장 높은 상대오차가 발생하는 것으로 나타났으나, 0.4% 미만의 매우 미소한 오차이므로 심도에 상관없이 우수한 성능을 보이는 것으로 판단할 수 있다.
3.3 주방식 광산의 패널광주 수직응력 평가
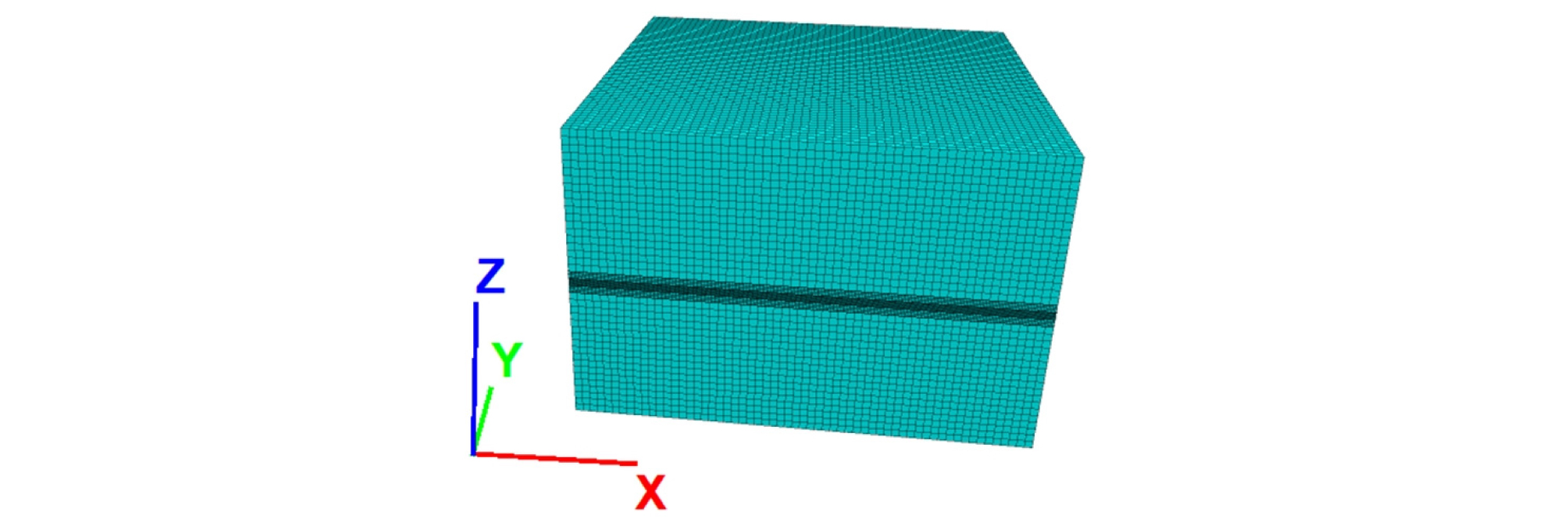
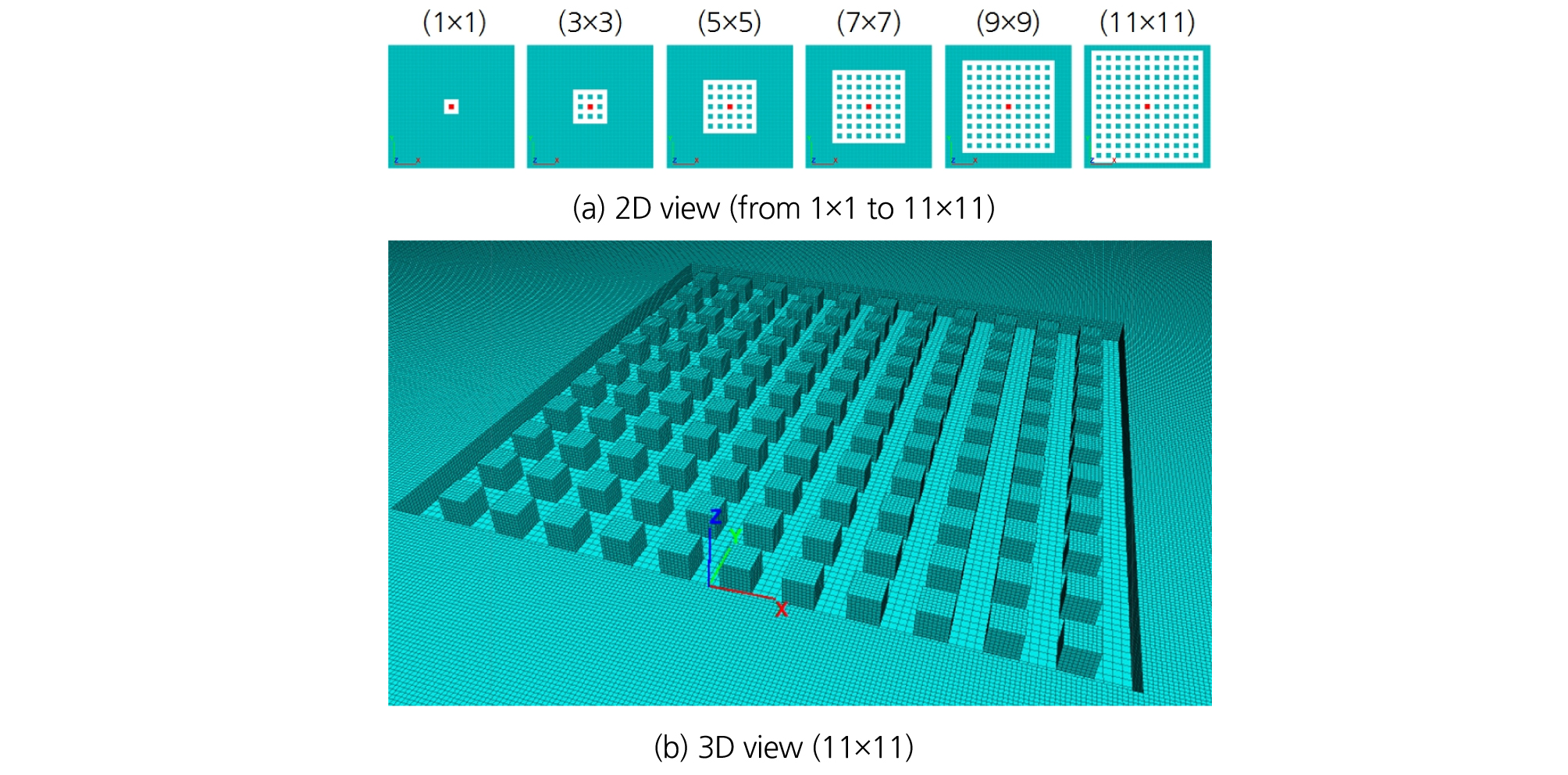
지류론 모델 검증을 통해 Case-B의 메쉬 크기 조합을 선정하고 FLAC3D 소프트웨어의 성능을 검증하였다. 검증에 이용한 모델과 동일한 물성과 메쉬 조합을 이용하여 Fig. 8과 같이 가로×세로×높이가 600 m×600 m×400 m인 연속체 암반 모델을 생성하고 안정화를 수행하였다. 이후, 광주 너비 10 m, 채광장 너비를 10 m로 설정하여 Fig. 9와 같이 목표 심도의 개발 영역 내에서 1개(1×1)~121 개(11×11)의 광주가 생성되도록 암반 내에 채굴적을 형성한 후, 해석을 재개하였다. 40 m~320 m까지 40 m 단위로 굴착심도를 변경하면서 동일한 과정을 반복하였다. 모델의 수렴 기준은 convergence 기본값인 평균 불균형력 비가 1E-5 미만인 경우로 설정하였으며, 전체 모델 크기에 비해 관심 영역의 크기가 과도하게 작은 경우에는 수렴 조건으로 국부 불균형력 1E-4를 적용하여 해석하였다. 모든 해석에서 개발 영역 내 중앙부에 위치한 광주의 수직응력이 주변 광주에 비해 다소 높은 편이므로, 이를 기준으로 이용하여 보수적으로 판단하고자 하였다. 개발 규모와 심도에 따라 중앙부 광주에 작용하는 수직응력 해석 결과는 Table 3과 같다.
Table 3.
The results of vertical stress at central pillar obtained from numerical tests
Note: (HOB : height of overburden (development depth), NP: number of pillar in a squared development area (development size), σP: vertical stress of pillar, σTAT: vertical stress of pillar estimated by tributary area theory, σvi: in-situ stress in vertical direction, VSF: vertical stress factor (σP /σvi))
4. 수치해석 결과 분석
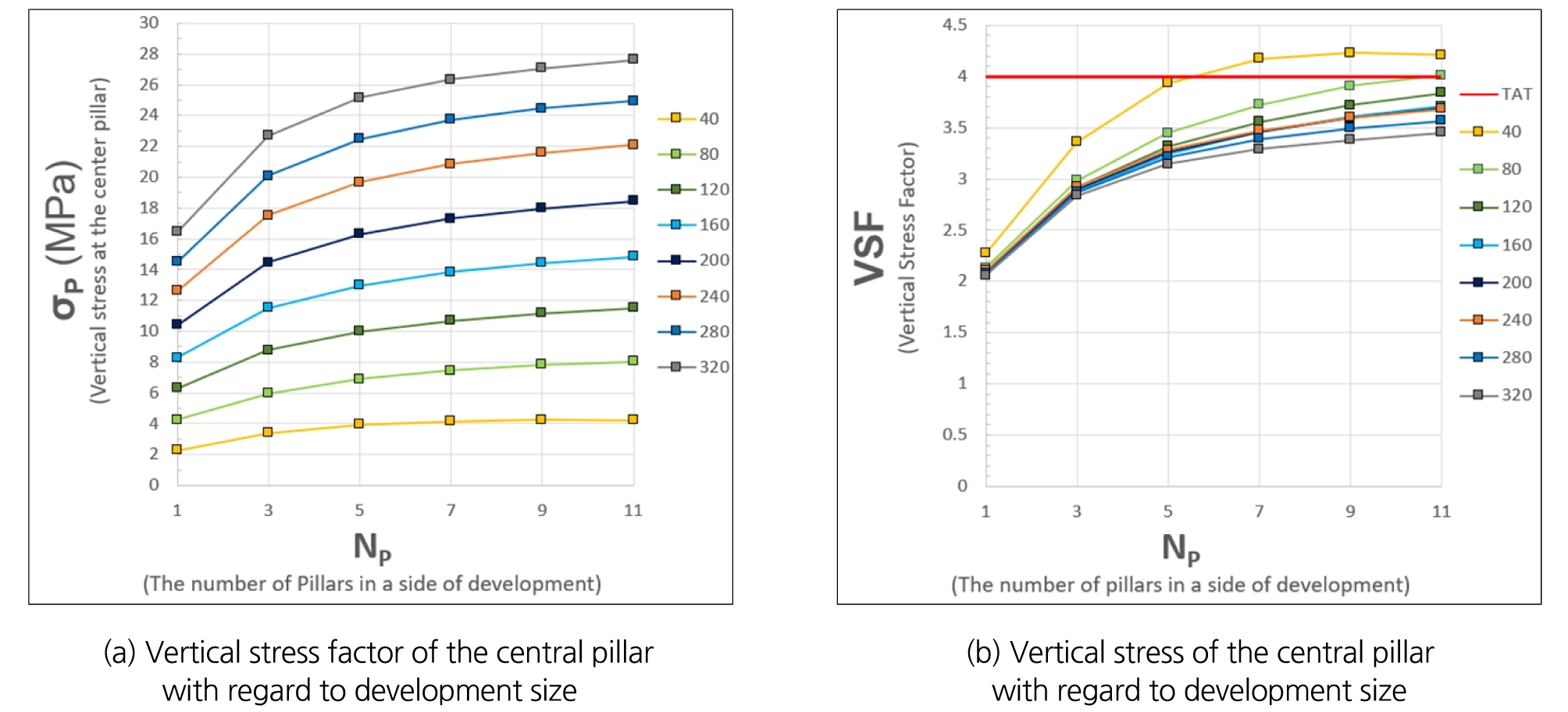
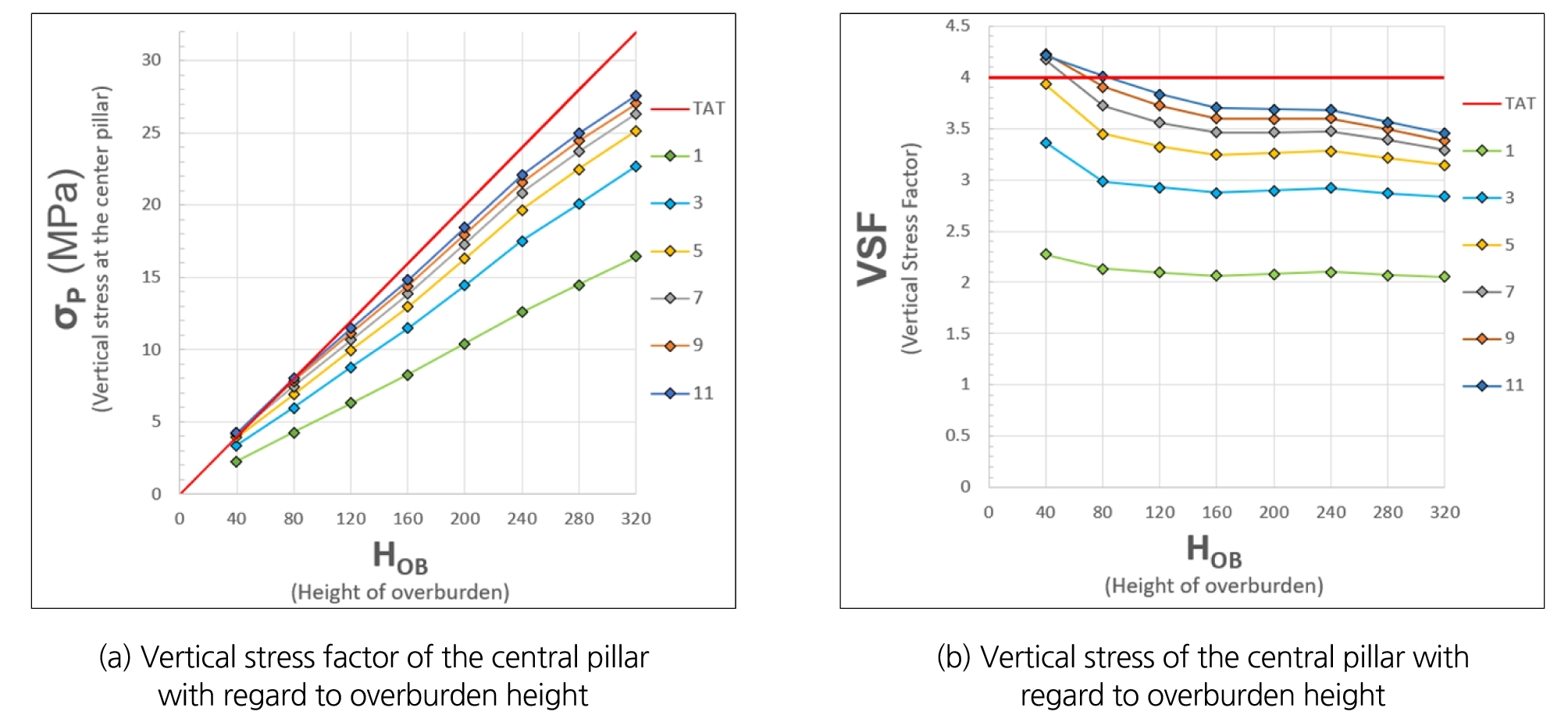
수치해석 결과를 이용하여 개발규모와 심도가 개발영역 내 중앙부 광주의 수직응력 수준에 미치는 영향을 분석하였다. 수직 방향으로 최대 변위가 발생하는 320 m 심도의 중앙부 광주에서는 광주 중간 부분에서는 국부적으로 인장파괴가 발생하였으나, 광주의 최상단 요소군에 포함되는 요소 중에서는 파괴가 발생하지 않았고, 해당 요소군은 여전히 선형탄성 구간 내에서 거동하고 있음을 확인하였다. 이에 따라 모든 해석 심도와 개발 규모에서 중앙부 광주의 최상단 요소군 수직응력 평균값을 지류론 추정값과 비교하여도 타당한 것으로 판단할 수 있다. 개발 규모와 심도 변화에 따른 중앙부 광주 수직응력은 각각 Fig. 10(a), Fig. 11(a)와 같다. 각 경우별 응력집중 수준을 비교하기 위해 중앙부 광주 수직응력 값을 채광장 굴착 전의 수직방향 현지응력 값으로 나누어 정규화한 수직응력계수(VSF, Vertical stress factor)를 이용하여 Fig. 10(b), Fig. 11(b)와 같이 나타내었다. Fig. 10에서와 같이 광주에 작용하는 수직응력은 심도가 동일한 경우에 개발 규모가 커질수록(광주 개수가 많아질수록) 다소 증가하다가 점차 수렴하는 경향을 보였다. 응력집중계수는 정사각형 개발영역 한 변의 광주 개수가 1인 경우(1×1개) 심도와 상관없이 약 2.1 정도로 유사한 값을 보였으며, 대부분의 경우에서 지류론 추정값보다 작은 것으로 나타나 지류론 추정 시 광주 수직응력이 과대평가되고 있음을 알 수 있다. 중앙부 광주의 수직응력계수는 개발 규모가 클수록, 저심도일수록 지류론 추정값에 근접한 값을 갖는 것으로 나타났다. 저심도인 40 m에서는 개발영역 한 변의 광주 개수가 5를 초과하는 경우(5×5개) 4.0 이상의 응력집중계수를 보여, 저심도에서 지류론 추정값을 초과하는 수준의 수직응력 발생 가능성을 확인하였다. Fig. 11에서와 같이 광주에 작용하는 수직응력은 개발규모가 동일한 경우에 심도가 깊어질수록 증가하는 경향을 보이며, 개발규모가 작을수록 심도에 따른 수직응력 증가율이 작은 것으로 나타났다. 동일한 개발 규모인 경우 심도가 증가함에 따라 수직응력계수가 특정 값에 수렴하는 연속된 경향성이 존재함을 확인하였다.
5. 결 론
본 연구에서는 3차원 유한차분법 프로그램인 FLAC3D를 이용하여 주방식 채광장을 모사하고 채광장 굴착으로 인해 패널 광주에 집중 작용하는 수직응력을 지류론 추정법에 의한 예측값과 비교 분석하였다. 수치해석 결과 개발 영역 내 중앙부 패널 광주에 작용하는 수직응력은 개발 심도가 저심도일수록, 개발 규모가 클수록 지류론 추정값과 유사한 값을 보였다. 따라서, 개발 영역 한 변의 길이가 200 m 이상의 수준으로 설계된 중대형 광산에서는 심도 100 m 이내의 천부에서 주방식 채광법 적용 시에 패널 광주에 작용하는 수직응력을 예측할 때 지류론으로 추정하더라도 상당히 높은 정확도로 예측 가능할 것으로 판단된다. 50 m 미만의 심도에서는 광주에 작용하는 수직응력이 지류론 추정값을 초과하는 수준까지 집중될 수 있으므로 주의를 요할 필요가 있다. 개발 규모가 충분히 크더라도 채광 심도가 깊어질수록 지류론 추정에 의한 오차가 증가하게 되며, 150 m 이상의 심도에서 수직응력이 대략 10% ~ 15% 가량 과대평가될 수 있다. 또한, 채광폭이 협소한 지하광산에서 지류론 추정을 통해 광주 수직응력을 계산하는 경우에는 심도와 개발 폭에 따라 최소 10% ~ 최대 50%까지 오차가 발생할 수 있을 것으로 판단된다.
상기의 수치해석 결과 및 분석은 3차원 수치 모의실험을 통해 지하광산 갱도의 굴착 심도와 개발 규모에 따라 패널 광주에 작용하는 수직응력의 변화를 관찰하여 수행한 정량적 분석 결과이다. 지하광산의 설계 시 광주에 작용하는 수직응력을 추정하기 위한 참고자료로 이용할 수 있으나, 이는 연속체 암반을 가정하여 해석한 결과이므로 주의할 필요가 있으며, 실제 현장에 적용하기 위해서는 추가 연구 및 현장 검증을 통해 충분한 실증과정이 필요하다.