1. 서 론
2. 이론적 배경
2.1 Bonded Particle Model
2.2 Smooth Joint Model
3. 관통 절리를 포함하는 광주의 강도 분석
3.1 석회석 물성에 해당하는 Micro-property 설정
3.2 관통 절리를 포함하는 광주의 강도 감소
4. 내포 절리를 포함하는 광주의 강도 분석
4.1 하나의 절리군을 포함하는 광주의 강도 분석
4.2 내포 절리로 인해 나타나는 절리선 길이의 총합과 광주 강도의 관계 분석
4.3 절리의 직경 분포의 종류와 광주 강도의 관계 분석
4.4 절리선 길이의 총합을 활용한 광주 강도식
4.5 두 절리군이 존재할 때의 광주 강도식
5. 결 론
1. 서 론
광산의 안전성 문제는 끊임없이 제기되고 있으며 특히 광산 내에서의 낙반·붕락 사고와 같은 광산 재해는 매년 꾸준히 발생한다(KORES, 2017). 이러한 광산 안전성은 광주의 강도와 밀접한 관련이 있으므로 광주의 강도를 예측하고 이에 따라 적절한 크기의 광주를 남겨두는 것은 필수적이라고 할 수 있다. 광주의 강도를 알고 있다면 현재 존재하는 광주의 위험성을 판단할 수 있고, 이에 따라 적절한 보강 등을 할 수 있다. 광주 내에는 다양한 불연속면이 존재하므로 광주의 강도는 광주를 구성하는 암석의 무결암 강도보다 낮다. 또한, 광주의 형상에 따라 강도가 바뀔 수 있다(Martin and Maybee, 2000, Esterhuizen, 2006). 미국의 NIOSH(The National Institute for Occupational Safety and Health)에서는 광주 관통 절리와 광주의 종횡비가 광주의 강도에 미치는 영향을 UDEC으로 분석하였다(NIOSH, 2011). 이 연구에서 광주의 강도는 불연속면의 경사각에 따라 변화하며, 종횡비가 증가하면 광주의 강도가 증가함을 보였고 이를 바탕으로 관통 절리와 종횡비에 따른 광주 강도 추정 방식을 제시하였다. 이때 전체 불연속면 중에서 광주를 관통하는 불연속면이 차지하는 비율을 나타내는 인자를 사용하므로 이 비율을 알아야 한다. 광주의 종횡비와 불연속면의 경사각이 경사진 광주의 강도에 미치는 영향을 FLAC 3D로 분석한 연구도 수행된 바 있다(Jessu and Spearing, 2019). 그러나 이 연구는 FDM(Finite Difference Method) 기반의 FLAC을 사용하였기 때문에 다수의 불연속면이 독립적으로 작용하는 광주의 거동을 설명하기 어렵다.
본 연구에서는 광주를 PFC(Partical Flow Code) 3D로 모델링하여 수치 해석을 진행하였다. PFC는 DEM(Distinct Element Method)을 기반으로 하여 물체를 강성 입자로 구성하는 bonded particle model을 사용한다. DEM은 물체를 작은 입자들의 모임으로 모델링하고 입자 간의 상호작용과 움직임을 해석하는 방법이다. DEM은 균열의 발생과 성장, 암반의 거동을 잘 모사하기 때문에(Itasca, 2008) 이를 활용한 인공시료 모델링을 통해 암석 등의 파괴와 거동을 수치적인 방법으로 분석하는 연구가 많이 수행되었다(Park and Min, 2017, Potyondy and Cundall, 2004). 절리는 암석의 거동에 영향을 미치며(Park et al., 2004, Cundall et al., 2008, Mas et al., 2008, Wanrui et al., 2016), 특히 광주 내에 존재하는 절리는 광주의 강도를 감소시킨다(Zhang et al., 2015). 그러나 절리에 의한 광주 강도 감소가 정량적으로 제시되지 않을 경우 광주의 강도를 평가하기에는 어려움이 따른다.
본 연구에서는 PFC 3D를 활용하여 광주 관통 절리면과 광주의 종횡비뿐만 아니라 내포 절리에 의한 광주 감소를 정량적으로 분석하여 광주 강도를 예측할 수 있는 식을 제안하였다.
2. 이론적 배경
2.1 Bonded Particle Model
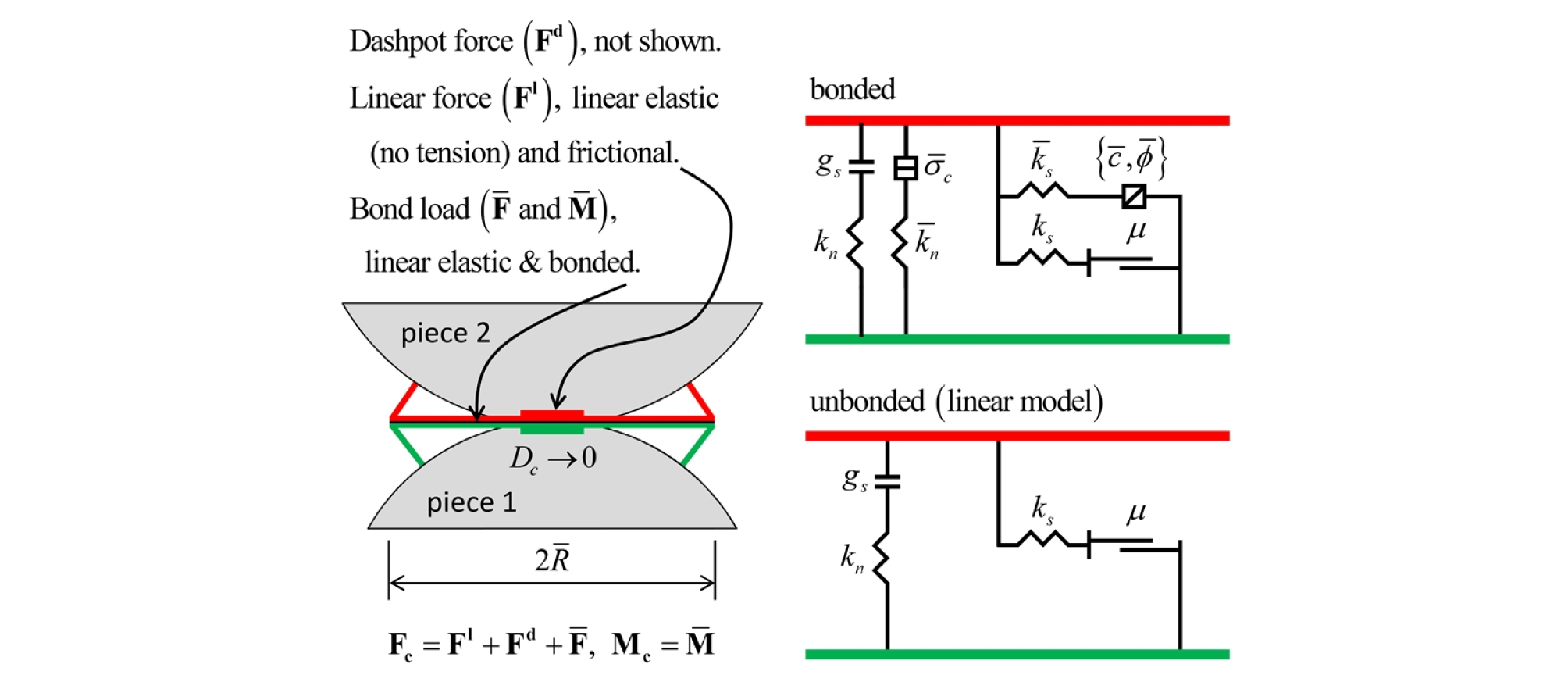
BPM(Bonded Particle Model)은 입자 간의 상호작용을 나타내는 방식으로, 실제 암석의 거동을 잘 모사하여 암석의 거시적인 거동을 예측할 수 있다(Potyondy and Cundall, 2004). 입자 간의 평행한 결합을 일정한 수직 강성과 전단 강성을 가지는 탄성 스프링으로 나타낸다(Itasca, 2008). BPM을 사용하여 물체의 물성을 나타내기 위해서는 입자 간의 상호작용을 나타내는 micro-property의 값을 설정해야 한다. 아래의 Fig. 1은 Linear Parallel Bond Model을 나타낸다.
2.2 Smooth Joint Model
Smooth Joint Model은 팽창(dilation)이 발생하는 경계면의 거동을 묘사한다. 마찰력이 작용하거나 결합된 상태의 절리면 거동은 입자 간의 경계면을 Smooth Joint Model로 모델링할 수 있다. 입자 간의 경계면은 결합이 끊어지기 전까지 선형탄성 거동을 하며, 결합이 끊어진 후에는 선형탄성 거동과 함께 마찰로 인한 팽창이 발생한다. 본 연구에서는 광주 내에 존재하는 절리면을 모델링하기 위해 Smooth Joint Model을 사용하였다.
3. 관통 절리를 포함하는 광주의 강도 분석
3.1 석회석 물성에 해당하는 Micro-property 설정
국내 석회석 광산에 기반한 암석 물성 데이터로 광주를 모델링하였다(Shin et al., 1996, Koo et al., 2008, Lee and Jang, 2010, Kim et al., 2012). 국내 광산은 대부분 높이가 약 7 m인 광주가 다수 존재하기 때문에 종횡비가 0.5이고 높이가 7 m인 원기둥 광주를 기준으로 하였다. Table 1은 각각 UCS가 76.5, 89.1, 102.5, 111.6, 121.0 MPa일 때의 micro-property 값이며, particle density는 2700 kg/m3이다. 이때, BPM을 이용하여 광주를 구성하는 입자 간의 결합을 정의하여 micro-property를 조절하였다(Lee and Song, 2006, Yang et al., 2006, Vallejos et al., 2016, Castro-Filgueira et al., 2017). UCS만의 변화에 따른 강도 변화를 분석하기 위해 탄성계수(E), 포아송비(ν)는 최대한 유사한 값을 가지도록 하였다. 점착력과 마찰각도 모두 현장 물성값과 유사한 값을 가지도록 하였으며, 각각 약 10 MPa, 약 40°이다.
Table 1.
Micro-properties for different UCS values
Table 2는 Table 1의 micro-property 값에 의한 각 광주의 물성을 나타낸다.
Table 2.
Mechanical properties of pillars
| UCS (MPa) | E (GPa) | ν |
| 76.5 | 45.2 | 0.21 |
| 89.1 | 40.8 | 0.19 |
| 102.5 | 46.1 | 0.20 |
| 111.6 | 48.2 | 0.21 |
| 121.0 | 47.6 | 0.21 |
Table 3은 광주의 중심을 지나는 관통 절리의 micro-property 값을 나타낸다. 이는 국내 절리면 물성과(Kim et al., 2001) 위의 UCS 범위에서 많이 사용되는 기존 연구의 값을 참조하였다(Cundall et al., 2008). 절리의 경사각과 양(quantity)에 의한 광주 강도 분석을 위해 절리 물성은 고정하였다.
Table 3.
Smooth Joint Model properties of joints
| Micro property | Description | Value |
| kn | Normal stiffness per unit area (GPa/m) | 200 |
| ks | Shear stiffness per unit area (GPa/m) | 20 |
| μ | Friction coefficient | 1.1 |
위의 물성값을 바탕으로 5가지 경우의 UCS에 대하여 관통 절리의 종횡비와 경사각을 변화시켜가며 강도를 시험하였다.
3.2 관통 절리를 포함하는 광주의 강도 감소
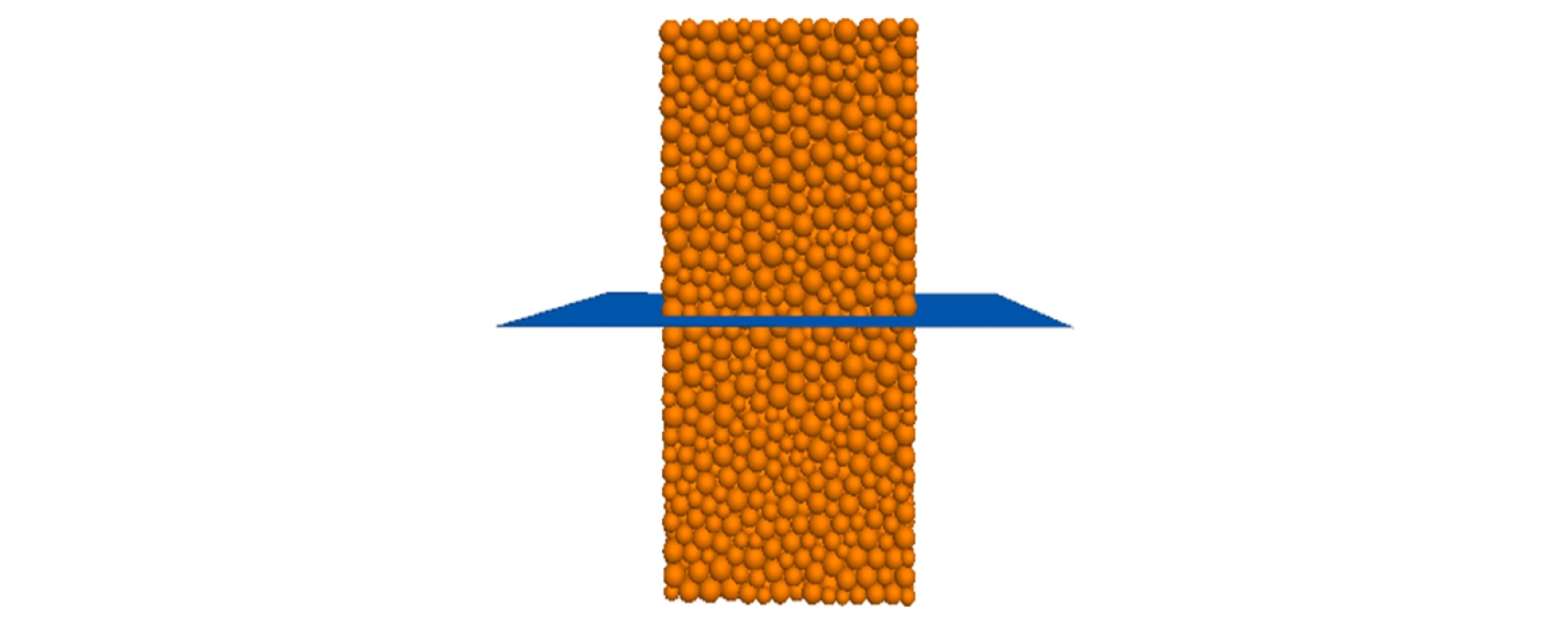
다섯 가지 경우의 UCS에 해당하는 물성값을 설정하기 위해 원기둥 모델을 사용하였으나 실제 광주는 직육면체와 유사하다. 이에 따라 광주 강도를 분석하기 위해 광주를 직육면체로 모델링하였다. 위의 물성값을 바탕으로 5가지 경우의 UCS에 대하여 광주의 종횡비와 관통 절리의 경사각을 변화시켜가며 강도를 얻었다. 먼저 UCS가 76.5 MPa이고 종횡비가 0.5(h=7 m)인 시료에 대해 관통 절리의 경사각을 0 ~ 90°범위에서 15°간격으로 변화시키면서 강도를 얻었다. 이후 광주 높이는 고정시키고 폭을 증가시키면서 종횡비가 1, 1.5일 때도 마찬가지로 관통 절리의 경사각을 변화시켜 강도를 확인하였다. 이 과정을 각기 다른 UCS를 가지는 광주들에 대해 반복한다. Fig. 2는 종횡비가 0.5이고 관통 절리의 경사각이 0°인 광주 모델을 나타낸다.
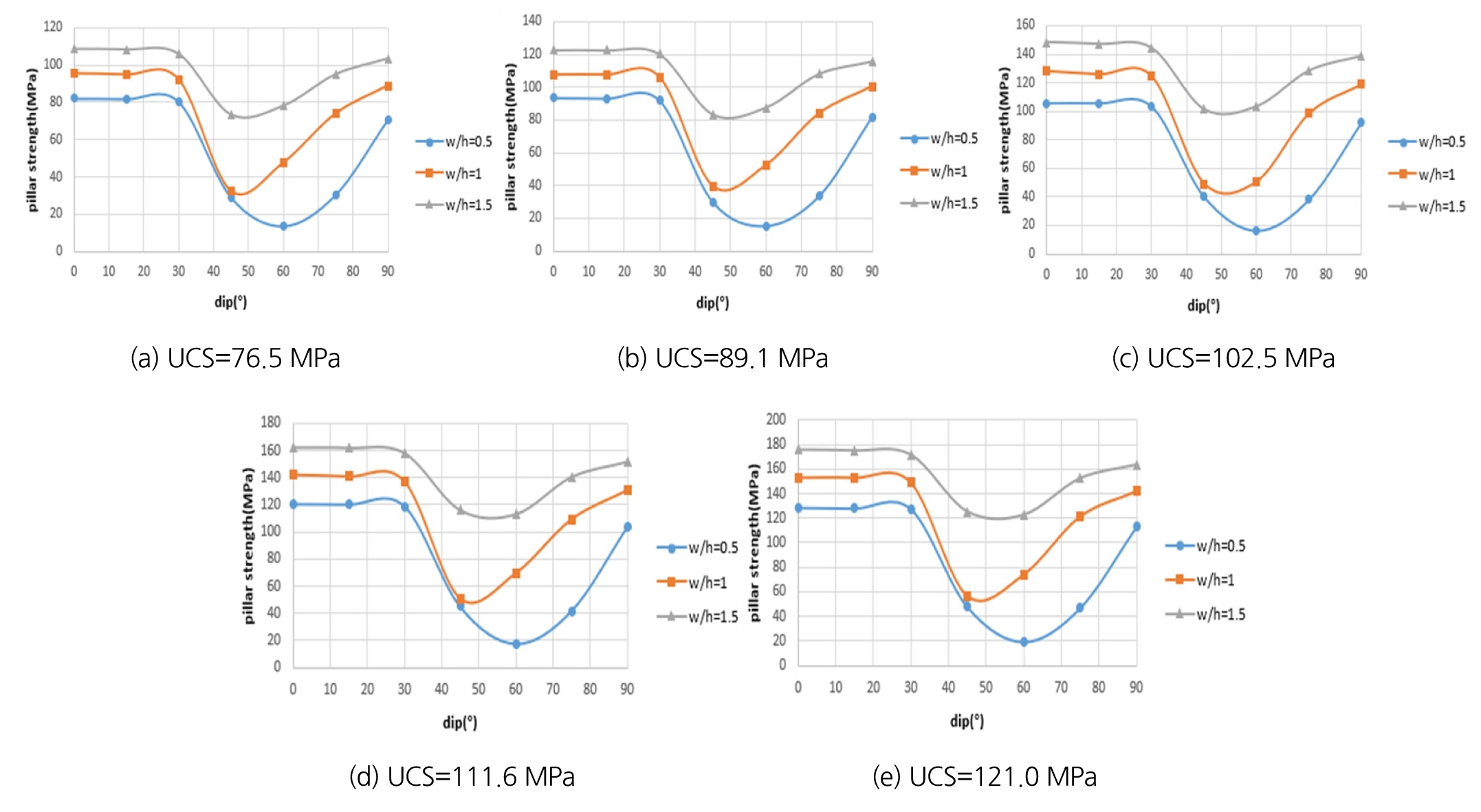
Fig. 3은 각각의 UCS에 해당하는 광주의 강도를 관통 절리의 경사각과 광주 종횡비(w/h)의 변화에 따라 나타낸 것이다. 가로축이 관통 절리의 경사각, 세로축은 광주 강도이다.
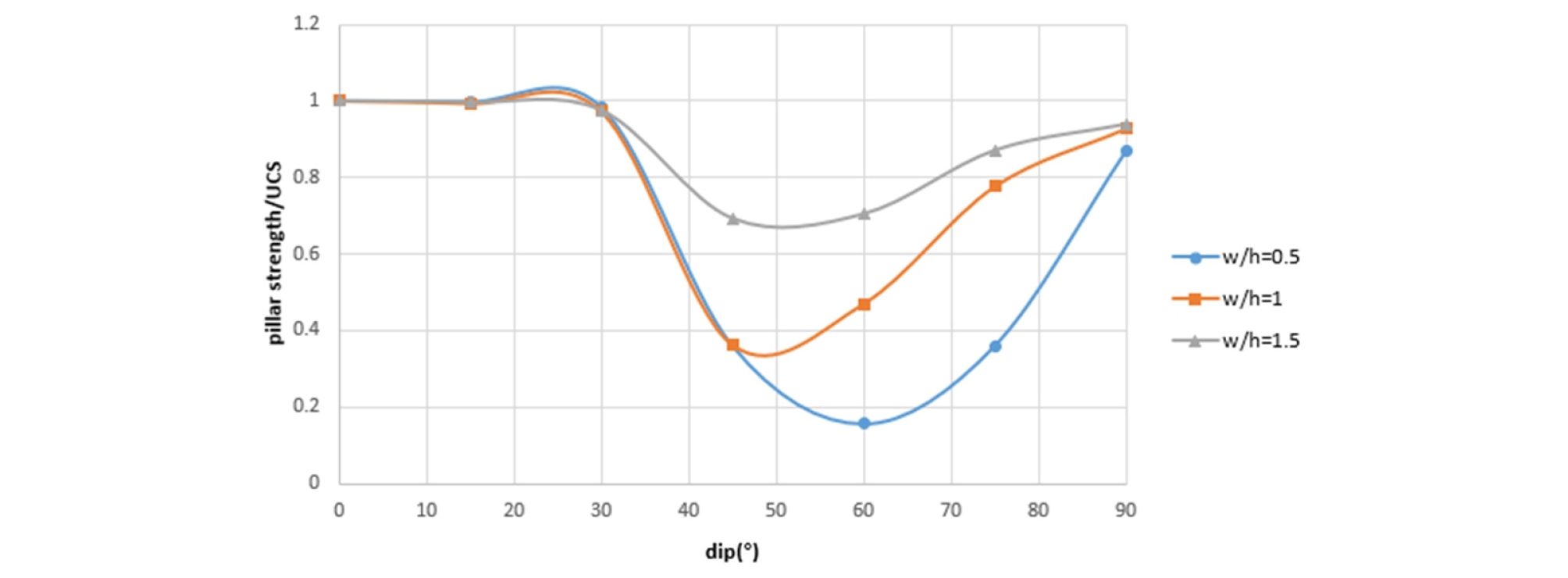
Fig. 3으로부터 불연속면의 경사각 변화에 따라 광주의 강도도 크게 변하는 것을 확인할 수 있다. 이러한 경향성은 이론적인 결과와도 일치한다. 또한, 종횡비가 커질수록 광주의 강도가 증가하며 경사각의 변화에 따른 광주의 강도 감소가 적다. 종횡비가 0.5인 경우에는 특정 경사각에서 강도가 급격히 감소하지만, 종횡비가 1.5인 경우에는 이러한 경향성이 작다. Fig. 4는 세로축이 광주 강도를 UCS로 나눈 값으로, 정규화한 결과이다. 이때 Fig. 3(a) ~ (e)를 각각 정규화한 후 평균값을 사용하여 도시하였다. 이로부터 UCS에 관계없이 종횡비와 관통 절리의 경사각을 통해 광주의 강도를 추정할 수 있다.
4. 내포 절리를 포함하는 광주의 강도 분석
NIOSH의 광주 설계 가이드라인에서는 광주를 관통하는 불연속면에 의한 강도 변화를 분석하였고, 광주 내부에 존재하는 수많은 작은 절리의 영향은 광주 강도에 0.65를 곱하여 일괄적인 비율로 강도를 감소시키는 방식으로 고려하였다. 그러나 광주 내부에 존재하는 소형 내포 절리들의 빈도와 크기, 방향 등의 차이가 광주의 강도에 영향을 미치는 것은 자명한 사실이므로 이에 대한 상세한 분석이 필요하다 할 수 있다. 이를 위해 수치 해석을 위한 광주 모델의 종횡비는 0.5, UCS는 81.6MPa(직육면체 기준)을 사용하였으며, 내포 절리면의 물성은 관통 절리의 물성과 같은 값을 사용하였다. Fig. 5는 내포 절리를 포함하는 광주 모델을 예시한다.
4.1 하나의 절리군을 포함하는 광주의 강도 분석
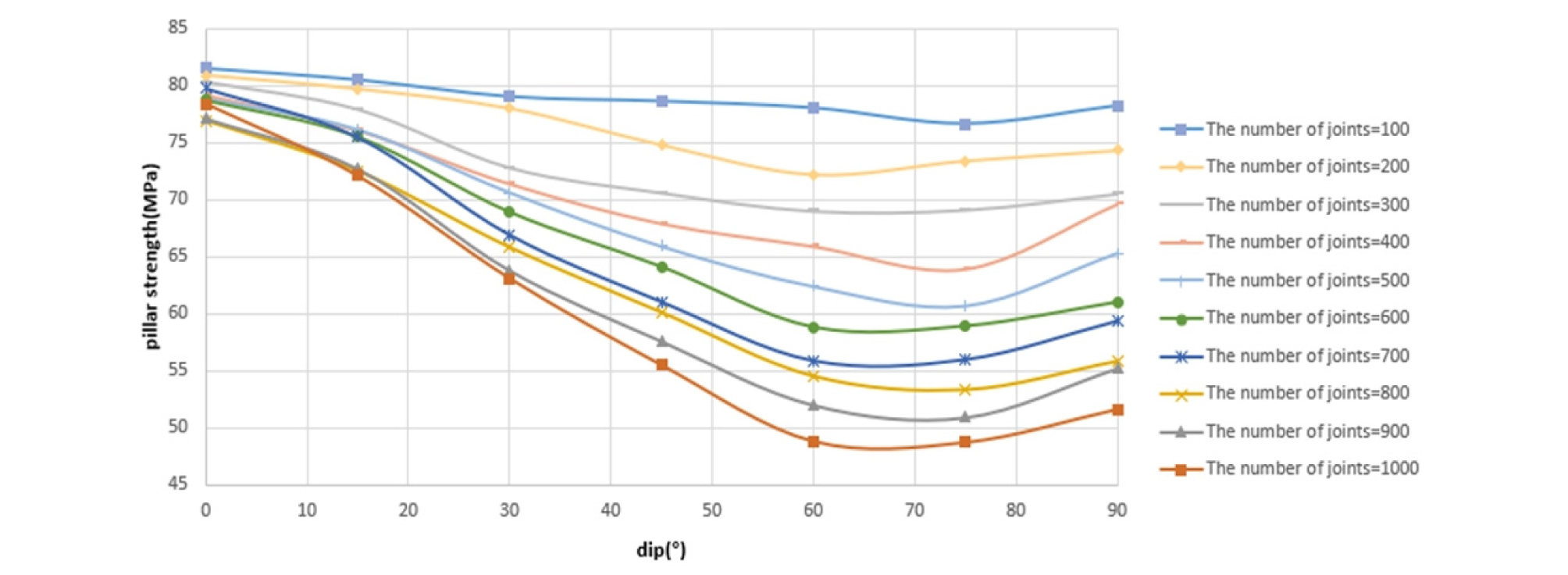
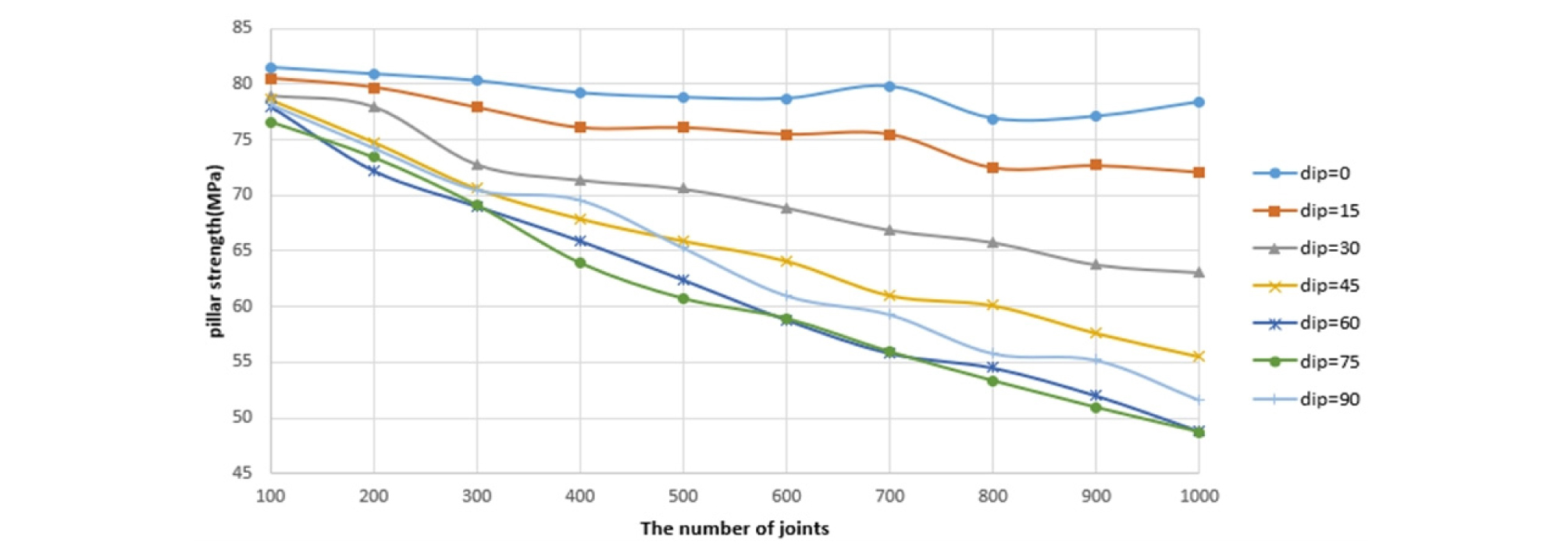
내포 절리의 지름이 0.3 ~ 0.5 m의 범위를 가지는 광주 모델의 강도를 측정하기 위해 절리의 개수를 100 ~ 1000개 범위에서 100개씩 증가시키고, 경사각은 0 ~ 90°범위에서 15°간격으로 변화시켰다. 절리 크기 분포는 음지수 분포(Negative exponential distribution)로 가정한다. 그 결과는 Fig. 6, Fig. 7과 같다.
Fig. 6은 가로축이 경사각이고, Fig. 7은 가로축이 절리의 개수인 그래프이며 이로부터 내포 절리의 경사각에 따라 강도가 변화하며 절리의 개수가 증가하면 강도가 감소하는 것을 확인할 수 있다. 이때 광주 강도는 경사각이 60 ~ 75°일 때 최소가 되며 내포 절리 수의 증가에 따라 광주 강도가 감소하나 그 감소 정도는 경사각에 따라 변화함을 알 수 있다. 즉 낮은 강도를 보이는 경사각일수록 내포 절리 증가에 따른 강도 감소 폭이 커진다고 할 수 있다.
4.2 내포 절리로 인해 나타나는 절리선 길이의 총합과 광주 강도의 관계 분석
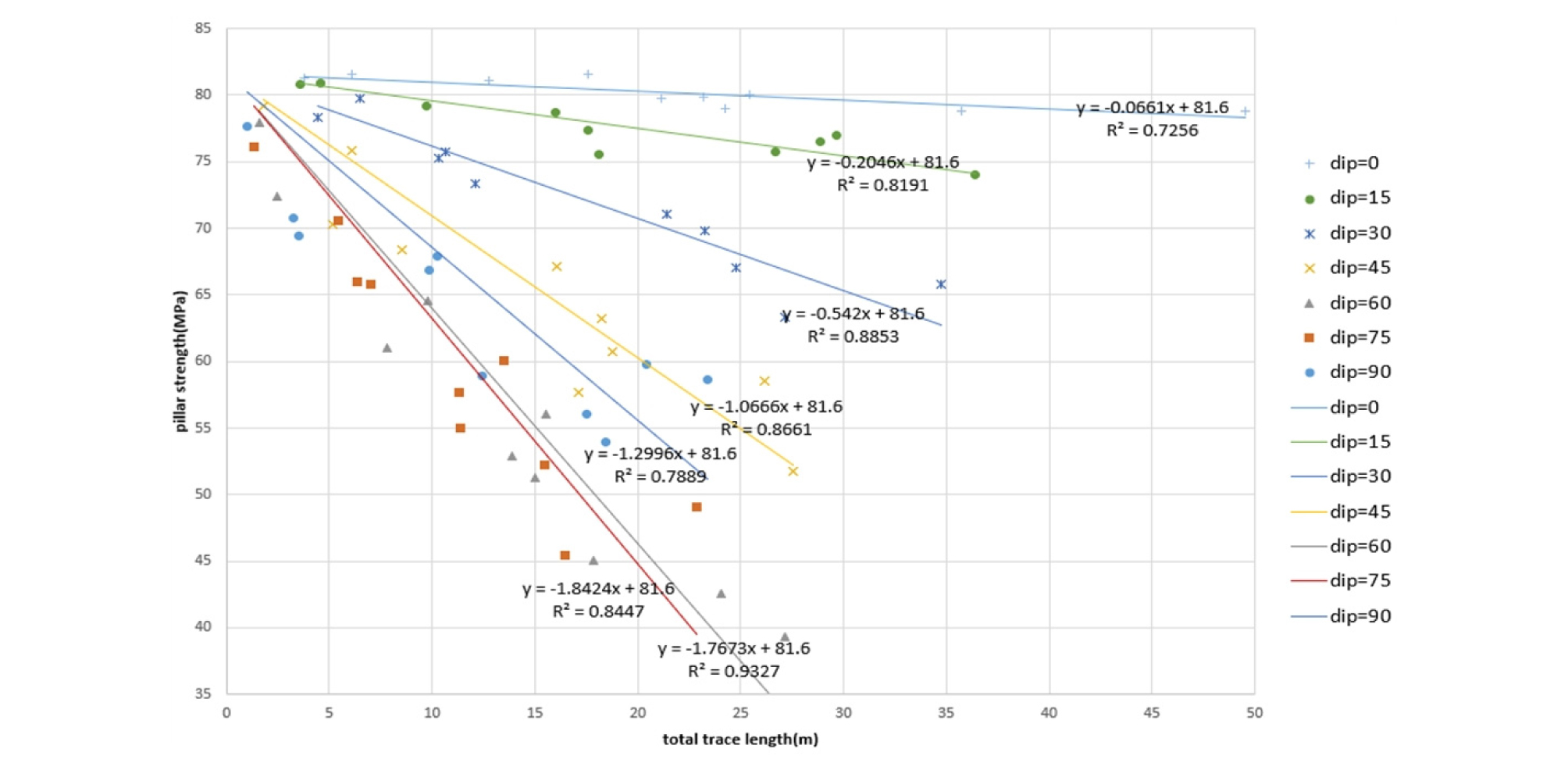
광주 내에 절리가 존재하면 광주 표면에서 절리선을 확인할 수 있으며 그 길이를 측정할 수 있다. 절리선 길이로부터 광주 강도를 예측하는 식을 제안하고자 한다. 절리선 길이는 현장에서 가장 직접적으로 측정이 가능하고 단순한 형태의 인자로 볼 수 있기 때문이다. 따라서 모든 절리선 길이의 총합과 광주의 강도 간의 상관 관계를 분석해보았다. 내포 절리의 직경 분포를 광주 너비의 5% ~ 50%의 범위인 0.175 ~ 1.75 m로 설정하고 절리 개수를 50 ~ 500개의 범위에서 50개 간격으로 하여 광주 내에 발생시킨 후 강도를 측정하였다. 이때 내포 절리의 직경은 음지수 분포(Negative exponential distribution)를 따른다. 광주 표면에 나타나는 절리선 길이는 MATLAB을 활용하여 절리 직경, 위치, 경사각 정보로부터 추출하였다. 이를 통해 절리선 길이의 총합을 x축으로 하고 광주 강도를 y축으로 하는 그래프를 도시하였다(Fig. 8). 절리선 길이의 총합이 0일 때에는 광주의 강도가 UCS와 같다고 가정할 수 있으므로, 추세선의 y 절편을 81.6 MPa로 고정하였다.
Fig. 8에서 각 경사각에 따라 절리선 길이의 총합과 광주 강도의 관계를 선형 회귀식으로 근사하였으며 상관계수 값이 모든 경사각에서 비교적 높게 나타났다. 따라서 광주 표면에 나타나는 절리선 길이로부터 광주 강도를 추정할 수 있음을 확인할 수 있다.
4.3 절리의 직경 분포의 종류와 광주 강도의 관계 분석
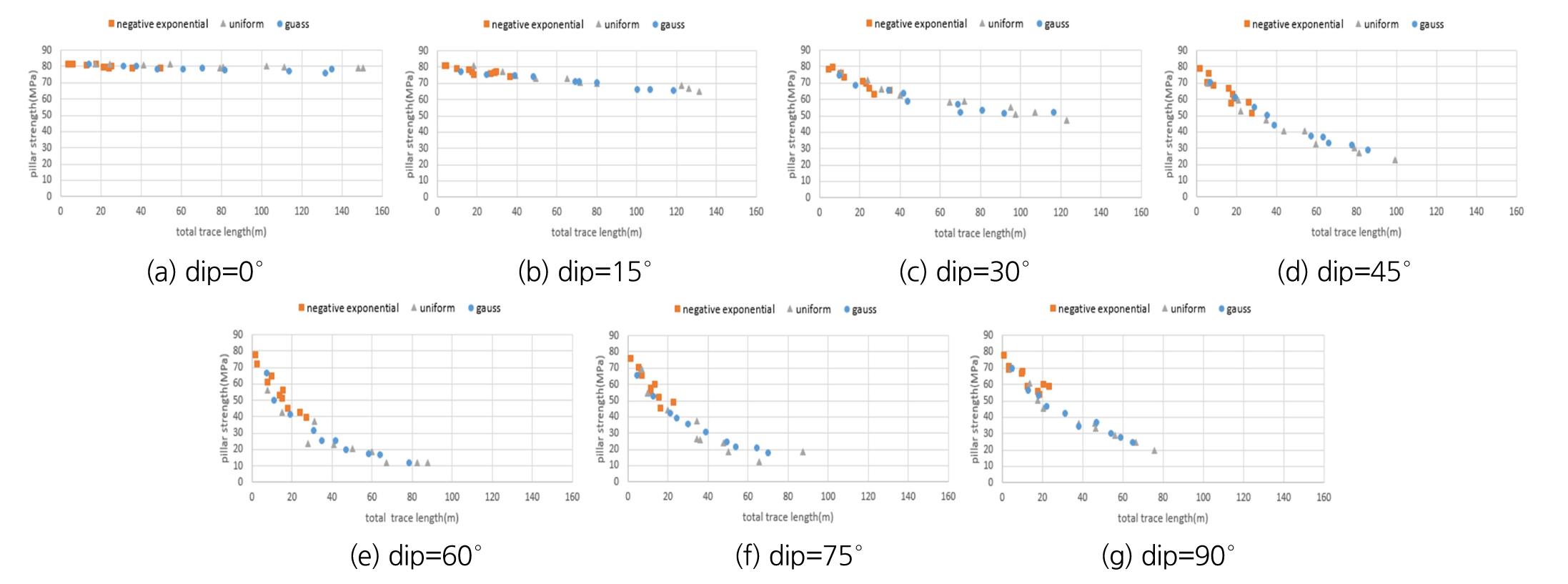
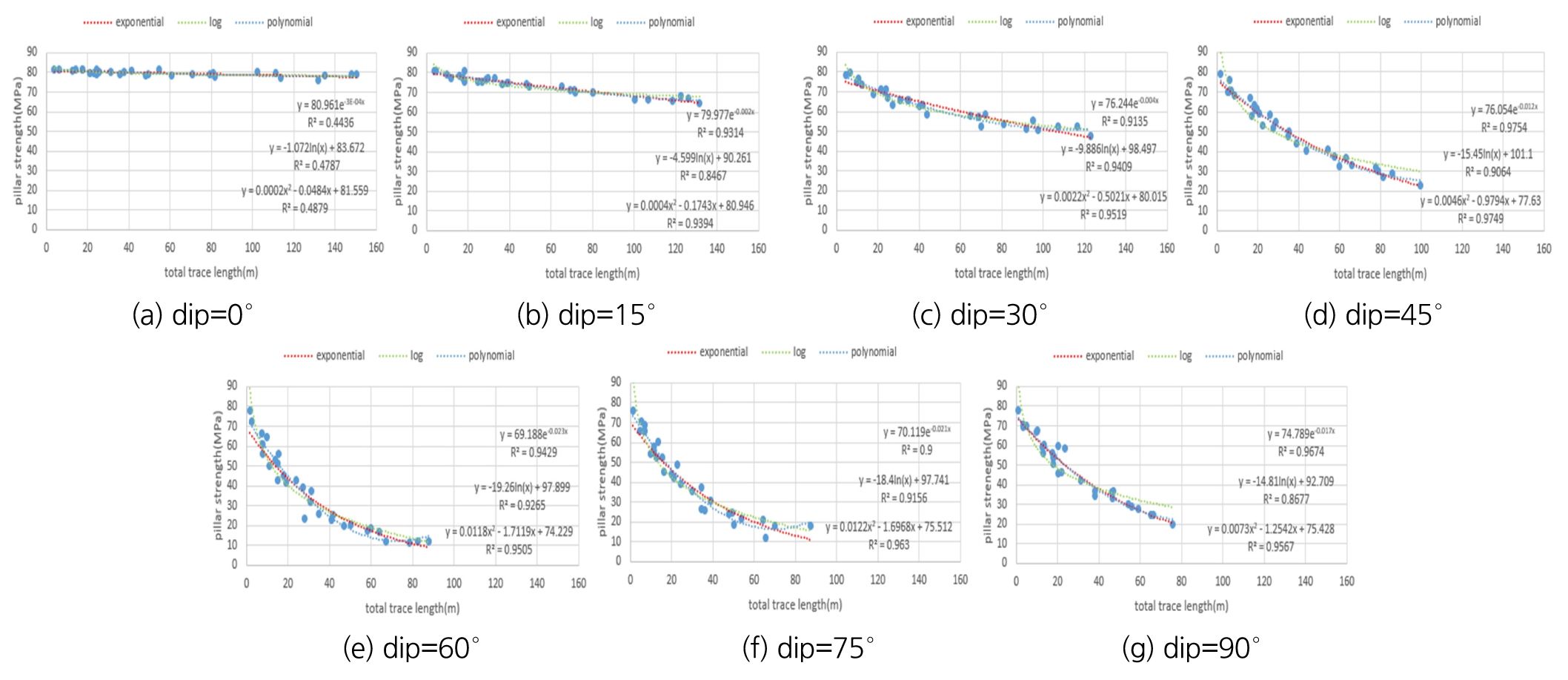
절리의 직경 분포의 종류에 따른 광주의 강도 변화의 경향성이 비슷하다면, 절리선 길이의 총합과 광주 강도의 관계를 단순화할 수 있다. 따라서 절리 직경이 음지수 분포(Negative exponential distribution), 균등분포(Uniform distribution), 정규분포(Gauss distribution)의 세 가지 분포를 따를 때 광주 강도 변화를 총 7가지의 경사각에 따라 Fig. 9와 같이 구하였다. 이때 정규분포의 평균은 0.9625m, 표준편차는 0.3m이다.
Fig. 9를 통해 절리의 직경이 각각 세 가지의 분포를 따를 때, 세 가지 분포에 따른 광주 강도를 나타내는 점들을 하나의 그래프에 도시하면 절리선 길이의 총합에 따른 광주의 강도가 일정한 경향성을 보임을 확인하였다. 따라서 위의 그래프들을 지수, 로그, 이차함수로 근사하고, y 절편을 UCS로 고정하였다. 그 결과는 Fig. 10과 같으며 그래프에서 회귀식과 상관계수 값은 위에서부터 차례로 지수, 로그, 이차함수로 회귀한 경우다.
위의 결과로부터 세 가지 직경 분포로부터 얻은 결과값을 함께 적용하여 서로 다른 세 개의 회귀식을 구하였을 때 각 경우에 상관계수 값이 충분히 높음을 알 수 있다. 세 종류의 함수 중 지수함수가 가장 적은 개수의 계수를 이용하여 나타낼 수 있으므로 절리선 길이의 총합과 광주 강도의 관계를 지수함수로 근사하고자 한다.
4.4 절리선 길이의 총합을 활용한 광주 강도식
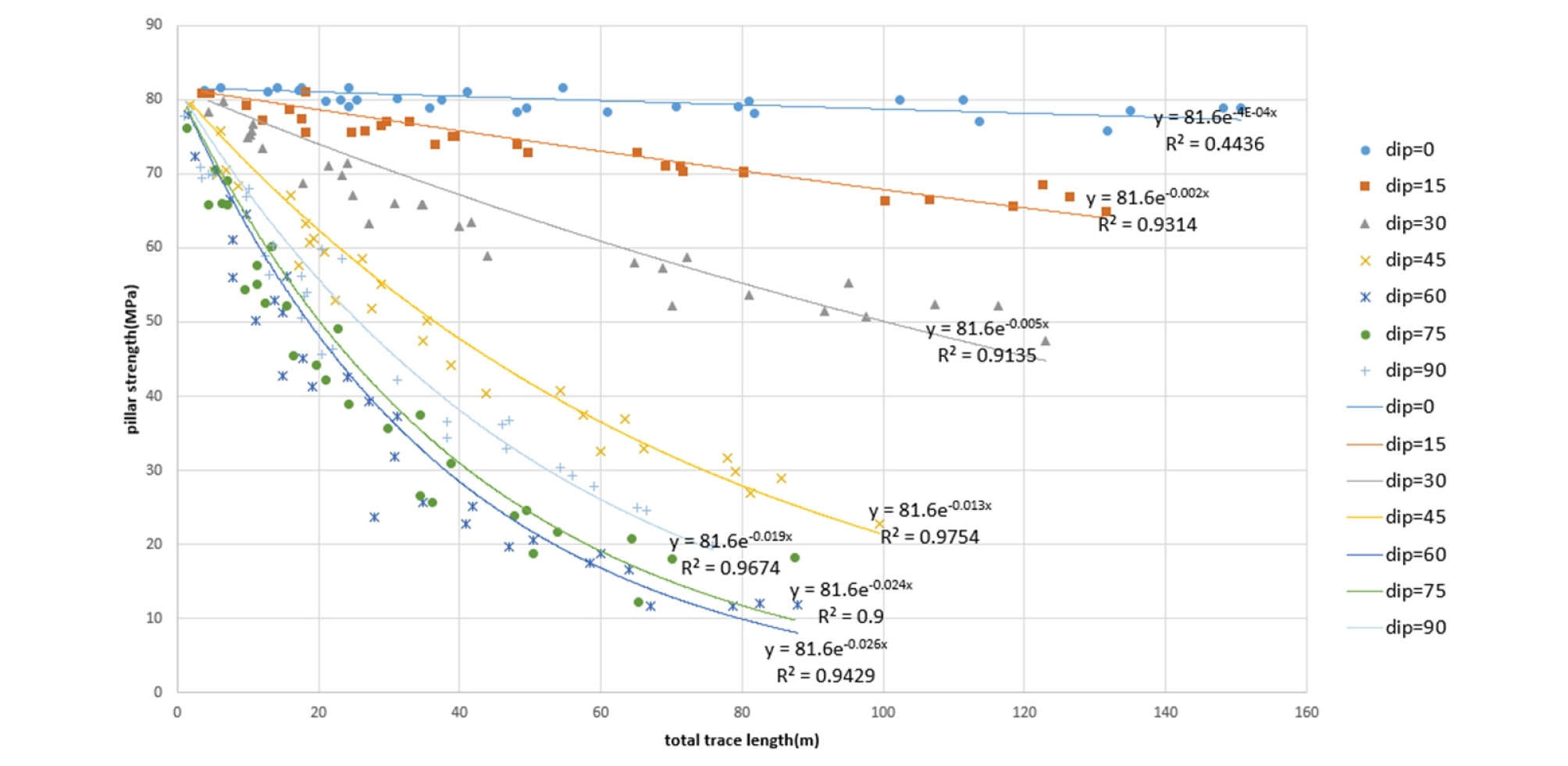
절리군의 절리선 길이의 총합과 광주 강도의 관계를 지수식으로 회귀하여 나타낸 결과는 Fig. 11과 같다. 이는 절리군의 경사각을 0 ~ 90°의 범위에서 15°간격으로 변화시켜가며 절리선 길이의 총합에 따른 광주 강도를 측정한 결과이다. y 절편은 UCS로 고정하였다.
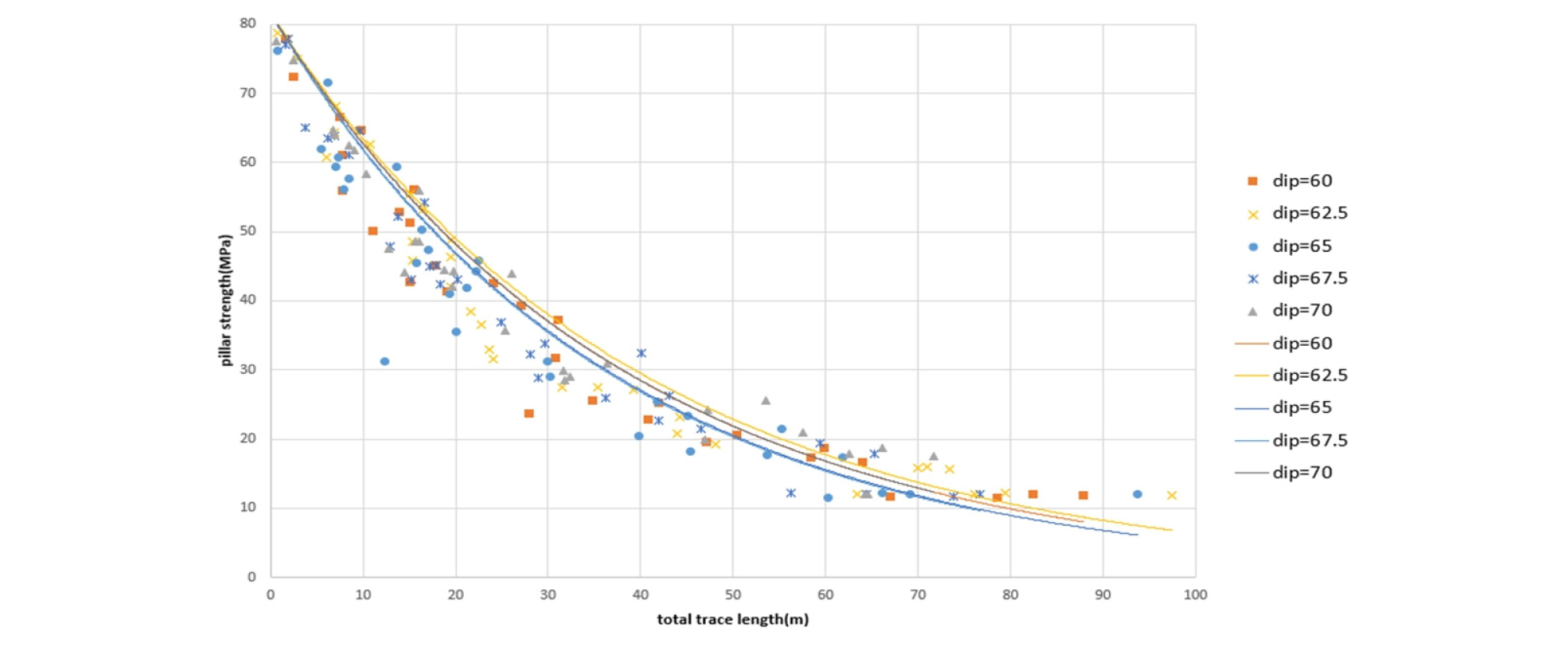
Fig. 11로부터 절리군의 경사각에 따라 절리선 길이를 이용하여 광주 강도를 예측할 수 있음을 확인하였다. 절리선 길이는 경사각이 커질수록 감소한다. 절리면의 경사각이 0°인 경우보다 90°인 경우에 광주 표면에 나타나는 절리선이 확률적으로 더 적으므로 실제와 유사한 경향성을 보인다고 할 수 있다. 경사각을 15°간격으로 변화시켜 광주 강도를 관찰한 위의 그래프에서는 경사각이 60°일 때 광주 강도가 가장 낮다. 광주 강도가 가장 낮게 나타나는 절리군의 경사각을 확인하기 위해 경사각이 60° ~ 70°의 범위에서 2.5°간격으로 변화시켜 광주 강도를 측정한 결과를 나타내었다(Fig. 12).
Fig. 12에서 각 절리군별로 지수함수 회귀식을 얻었으며, 지수의 절댓값은 Table 4와 같다.
Table 4.
Absolute values of the exponents of regression equations
| Dip (°) | 60 | 62.5 | 65 | 67.5 | 70 |
| Absolute value of the exponent | 0.026 | 0.025 | 0.028 | 0.028 | 0.026 |
Table 4에서 경사각이 60°인 경우와 경사각이 70°인 경우의 회귀식의 지수가 같다는 것을 확인할 수 있다. 또한, 경사각이 65°, 67.5°일 때의 지수의 절댓값이 가장 크기 때문에 경사각이 65°부근에서 광주 강도가 가장 낮다. 경사각이 65°인 경우를 기준으로 지수의 절댓값이 대칭성을 보이므로 광주 강도는 절리군의 경사각이 증가함에 따라 경사각이 65°까지는 감소하였다가 다시 증가한다고 볼 수 있다.
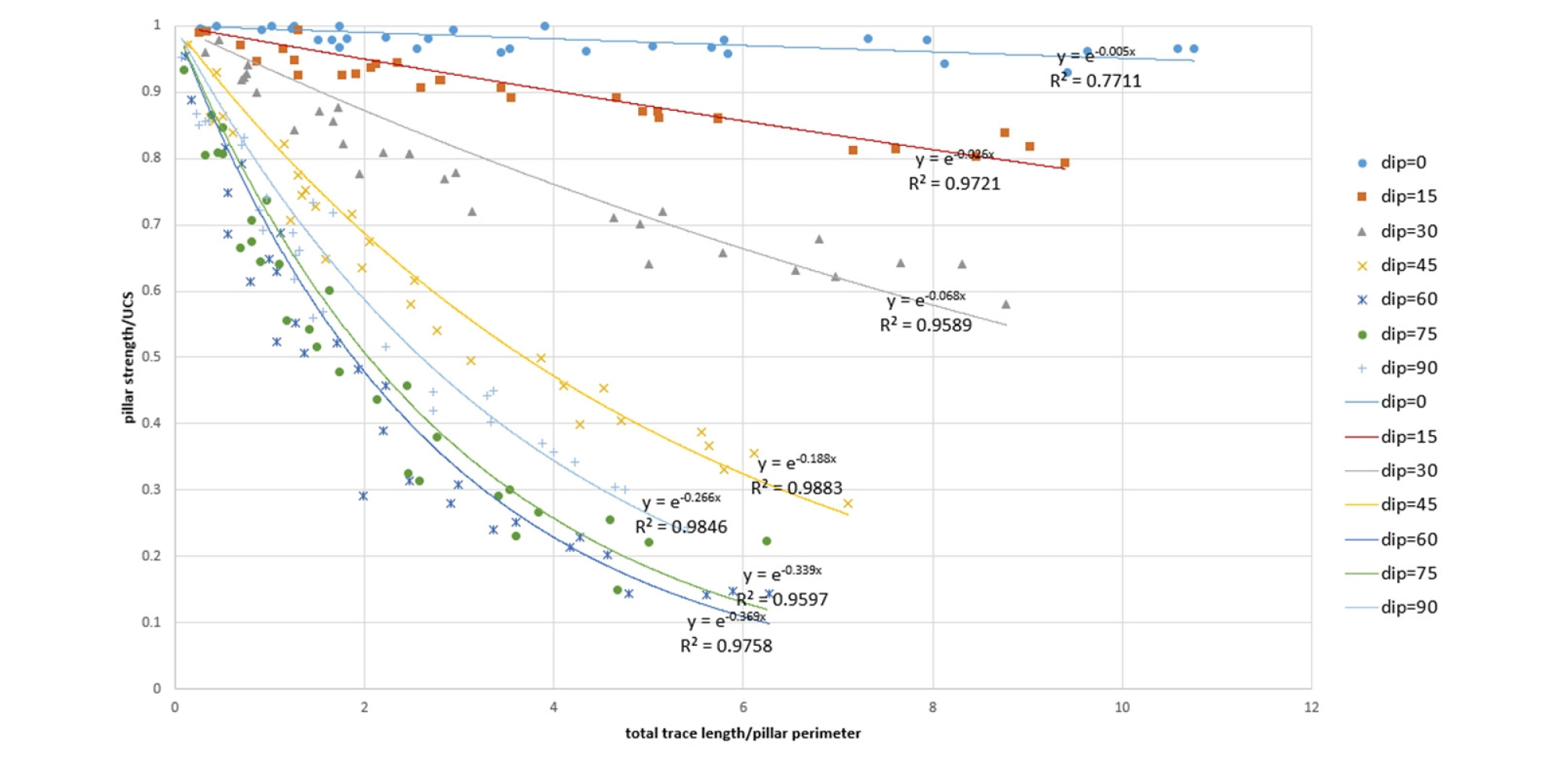
Fig. 13은 임의의 UCS를 가지는 광주의 강도를 예측하기 위해 Fig. 11을 정규화였다. 가로축은 절리선 길이의 총합을 광주 둘레 (14m)로 나누고, 세로축은 광주 강도를 UCS (81.6MPa)로 나누었다. 동일 광주 길이로 정규화하였으므로 이에 따른 결과 차이는 없다. Table 5는 Fig. 13의 절리의 경사각에 따른 회귀식의 지수의 절댓값 (pa)을 나타내며, 식 (1)은 광주 강도 추정 식이다. 광주 표면에 나타나는 절리선 길이의 총합 (La)과 지수 (pa)를 식 (1)에 대입하여 광주 강도를 예측할 수 있다.
Table 5.
Absolute values of the exponents of regression equations
| Dip (°) | 0 | 15 | 30 | 45 | 60 | 75 | 90 |
|
Absolute value of the exponent (pa) | 0.005 | 0.026 | 0.068 | 0.188 | 0.369 | 0.339 | 0.266 |
| $$\mathrm{광주}\;\mathrm{강도}=UCS\;\times\;Se^{-p_ax}\;(\mathrm 단,\;x\mathrm 는\;L_a/\mathrm{광주둘레})$$ | (1) |
Table 5에 제시되지 않은 절리의 경사각이 존재하는 광주 강도를 예측하기 위해서는 해당 경사각에 가까운 두 경사각에 해당하는 강도 추정 식으로부터 얻은 광주 강도 값들을 이용하여 Fig. 13에서 근사적으로 추정해야 한다. 광주 강도는 절리군의 경사각이 증가함에 따라 경사각이 65°부근까지는 감소하였다가 다시 증가한다는 것을 고려해야 한다.
광주 강도 분석을 통해 내포 절리의 경사각에 따라 광주 강도 감소 폭이 다르며, 절리선 길이의 총합과 광주 강도의 관계를 지수함수로 근사할 수 있음을 확인하였다. 식 (1)을 이용하여 절리선 길이의 총합만으로 광주 강도를 예측할 수 있다.
4.5 두 절리군이 존재할 때의 광주 강도식
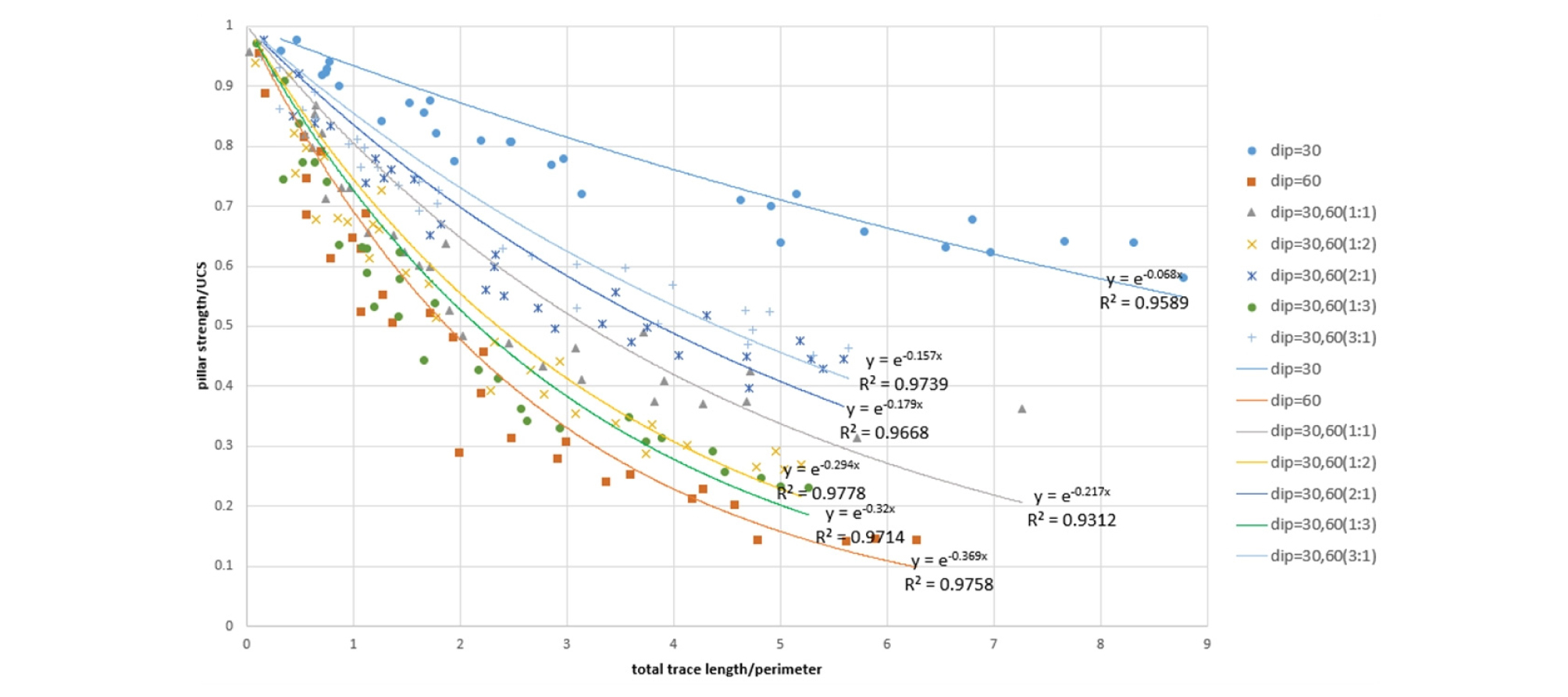
식 (1)을 통해 하나의 절리군에 의한 광주 강도 추정 식을 제시하였다. 그러나 지하 광산에는 다수의 절리군이 존재하여 광주 내에 다양한 경사각의 내포 절리가 분포하는 경우가 많으므로 식 (1)만으로 광주 강도를 예측하기에 충분하지 않을 수 있다. 두 개의 절리군이 광주 내에 동시에 존재할 때 광주 강도를 예측하고자 경사각이 30°, 60°인 절리군을 사용하여 절리선 길이의 총합에 따른 광주 강도를 관찰하였다. 경사각이 30°, 60°인 절리군을 사용하여 절리 개수의 상대적인 비율에 따른 광주 강도의 경향성을 확인하고자 하였다. 이에 따라 경사각이 30°, 60°인 절리 개수를 총 5가지의 비율인 1:1, 1:2, 2:1, 1:3, 3:1로 설정하여 내포 절리를 광주 내에 발생시켰다. 이때 두 절리군의 경사 방향은 90°로 같다. 이때 두 절리군의 개수 비율에 따른 절리선 길이 비율의 평균값을 Table 6에 나타내었다. Fig. 14는 두 절리군이 존재할 때 광주 강도를 나타내며, y 절편은 UCS로 고정하였다. 가로축은 절리선 길이의 총합을 광주 둘레로 나누고, 세로축은 광주 강도를 UCS로 나눠서 정규화하였다.
Table 6.
The ratio of the number of two joints and the ratio of trace length
| The ratio of the number of two joints (dip= 30°,60°) | 3:1 | 2:1 | 1:1 | 1:2 | 1:3 |
| Mean value of the ratio of total trace length | 3.79:1 | 2.62:1 | 1:0.8 | 1:2.39 | 1:2.52 |
두 절리군이 서로 다른 비율로 존재할 때 회귀식의 지수를 예측하기 위해 Table 6의 평균 절리선 길이 총합 비율을 사용하여 단일 절리군만 존재하는 경우의 지수들로부터 선형 비율로 보간하였다. 이 값들과 Fig. 14의 추세선의 지수들을 비교하여 상대오차를 Table 7에 나타내었으며, 상대오차의 평균은 10.83%이다.
Table 7.
Prediction of the exponents with the ratio of trace lengths
예측의 정확도를 높이기 위해 절리선 길이 총합의 비율에 따라 예측한 지수 값에 1.1을 곱하여 경사각이 60°인 절리군에 가중치를 주었으며, 그 결과는 Table 8과 같다.
Table 8.
Prediction of the weighted exponents with the ratio of trace lengths
Table 8에서 평균 오차율은 4.76%로 가중치가 없을 때인 10.83%와 비교하여 상대오차가 크게 감소했다. 측정한 절리선 길이 총합 비율에 1.1을 곱하여 지수를 예측한 후 광주 강도를 예측하는 것이 타당하다. 경사각이 각각 60°, 30°이고 경사 방향이 같은 절리군이 존재할 때 절리선 길이를 이용하여 광주 강도를 추정하기 위해 식 (2)를 제안하였다. 경사각이 각각 60°, 30°인 절리군의 절리선 길이의 총합 (La, Lb)을 각각 구한 후 식 (2)에 대입하여 광주 강도를 추정할 수 있다. 단, 식 (2)에서 pa, pb는 Table 5의 경사각이 60°, 30°일 때의 값으로, 각각 0.369, 0.068이다.
| $$\mathrm{광주}\;\mathrm{강도}=UCS\;\times\;e^{-1.1\lbrack p_b+(p_a-p_b)\;\frac{L_a}{L_a+L_b}\rbrack x}\;(\mathrm 단,\;x\mathrm 는\;(L_a+L_b)/\mathrm{광주둘레})$$ | (2) |
식 (2)는 경사각이 더 큰 절리군에 대한 가중치를 부여하여 광주 강도를 높은 정확도로 예측할 수 있다. 두 절리군의 절리선 길이의 총합 비율만으로 간편하게 광주 강도를 추정할 수 있다.
5. 결 론
PFC 3D의 수치 모델을 이용하여 광주가 관통 절리 또는 내포 절리를 포함할 때 광주의 강도를 분석하였다. 광주가 관통 절리를 포함하는 경우 광주의 강도는 불연속면의 경사각에 영향을 받으며, 광주의 폭이 증가할수록 광주의 강도가 증가함을 확인하였다. 관통 절리의 경사각과 광주의 종횡비를 이용하여 광주의 강도를 추정하는 방법을 제안하였다. 광주가 내포 절리를 포함하면 광주 강도가 감소한다. 내포 절리로부터 얻을 수 있는 절리선 길이의 총합과 광주 강도와의 관계를 지수함수로 회귀하여 높은 상관계수를 얻었다. 이로부터 절리선 길이의 총합을 이용하여 지수 함수식을 통해 광주 강도를 추정하는 방법을 제시하였다. 나아가 경사각이 60°, 30°인 두 절리군이 존재할 때 각 절리군의 절리선 길이의 총합의 비율로부터 광주 강도를 추정하는 방법을 제안하였다. 지수함수 회귀식으로 강도 추정 시, 절리선 길이 총합 비율에 따라 예측한 지수 값에 1.1을 곱하여 예측의 정확도를 높일 수 있었다. 이러한 방법은 광주의 표면에 드러난 절리선 길이만 필요하기 때문에 광주 강도를 용이하게 추정할 수 있다는 장점이 있다.
본 연구에서는 경험적으로 추론되는 광주 강도의 경험식을 PFC 3D를 통해 불연속면의 분포 특성을 고려하여 정량적인 분석을 수행하였다. 광주를 관통하는 절리에 의한 광주 강도 변화 결과가 UDEC을 활용한 NIOSH의 결과와 유사하므로 PFC를 이용한 평가가 가능하다. 내포 절리에 의한 광주 강도 변화 정량화를 위해 이후의 과정을 수행하였다. 그 결과, 수치로만 제시되었던 경험적 감소계수를 불연속면 분포 특성을 고려한 정량화가 가능하였다. 하지만 두 절리군이 존재하는 경우, 특정 경사각에 대해서만 강도 추정 식을 제시하여 제한적이라는 한계가 있다. 이에 따라 본 연구를 발전시켜 더 넓은 범위의 조건에서 광주의 강도를 추정할 수 있는 식을 개발할 필요가 있다.