1. 서 론
2. 해석모델 개요
2.1 DECOVALEX-2019 Task B
2.2 Step 1: Benchmark test
2.3 TOUGH-FLAC 연동해석
3. 해석 결과 및 토의
3.1 역학적 거동
3.2 수리학적 거동
3.3 Task B 연구현황
4. 요약 및 결론
1. 서 론
최근 심부 지층으로의 유체 주입에 의한 단층 재활성화 문제와 유도지진 문제가 국내외적인 관심사로 대두되었다. 이산화탄소나 폐기물의 지중처분, 인공저류층 지열발전, 천연가스 지하저장, 원유의 2차 회수 등을 목적으로 하는 심부 지층 내 유체 주입은 지층의 응력조건에 영향을 미쳐 불안정성을 야기할 수 있으며, 인접한 단층의 전단저항력을 저하시켜 미끄러짐 및 인공 지진을 유발할 수 있다. 유체 주입에 따른 단층의 재활성화는 수리-역학적으로 연계된 복합거동으로서 이를 적절하게 이해하고 예측할 수 있는 기술의 개발은 지반의 안정성뿐만 아니라 인접 지역의 주민 수용성을 고려할 때 매우 중요한 과제라고 할 수 있다(Rutqvist et al., 2013).
단층의 재활성화 문제를 평가하기 위한 기법은 크게 해석적인 방법(analytic method)과 수치적 방법(numerical method)으로 나눌 수 있다. 해석적인 방법은 단층에 작용하는 수직응력과 전단응력, 압력의 관계로부터 단층의 전단파괴 가능성을 개략적으로 평가하는 방법으로서 주로 Mohr-Coulomb 파괴기준이 사용된다. 이를 이용하면 현지의 응력조건에서 단층의 미끄러짐을 유발할 수 있는 압력(critical injection pressure)과 단층의 방향에 따른 안정성을 예측할 수 있다(Wiprut & Zoback, 2002, Vidal Gilbert et al., 2010). 그러나 해석적인 방법은 대상에 대한 여러 가지 가정과 단순화를 전제하기 때문에 유체 주입 중 발생할 수 있는 지층의 복합적인 거동과 단층의 상호작용을 반영하기 어려우며, 수치해석적 접근을 통해 이러한 문제점을 극복할 수 있다(Bohloli et al., 2015).
수치해석적 방법은 역학적 관점에서 단층을 불연속면으로 고려할 것인지, 등가의 연속체로 고려할 것인지에 따라 두 가지 접근법으로 대별할 수 있다. 전자는 연속체 모델(유한요소법, 유한차분법) 또는 불연속체 모델(개별요소법) 내에 불연속면을 정의함으로써 단층의 개폐(opening and closing)나 미끄러짐(slip)을 직접적으로 재현하는 방법이다(Vidal-Gilbert et al., 2009, Cappa and Rutqvist, 2011, Orlic et al., 2011, Cuisiat et al., 2010, Morris et al., 2011). 반면, 후자는 단층을 일정 두께를 갖는 연속체의 일부로 가정하는 방법으로 단층 물성에 상응하는 등가의 연속체 물성을 통해 단층의 거동을 구현하도록 하는 방법이다(Gudmundsson, 2004, Rinaldi et al., 2014, Rutqvist et al., 2015). 모델링 기법에 따라 서로 다른 가정과 장단점을 내포하고 있으며, 이에 대한 선택은 관심 영역의 스케일, 암반의 상태나 불연속면의 발달 정도, 가정된 단층 구성모델의 물성 획득 여부 등에 따라 좌우된다(Leijon, 1993, Bohloli et al., 2015).
본 연구는 유체의 주입에 따른 단층 활성화를 모사하기 위한 수치해석 연구로서 DECOVALEX(DEvelopment of COupled models and their VALidation against EXperiments) 프로젝트의 일환으로 수행되었다. DECOVALEX 프로젝트는 고준위 방사성폐기물의 지층처분을 고려하는 세계 각국을 중심으로 1992년부터 수행된 국제공동연구로서 방사성 폐기물 처분장에서의 공학적 방벽과 지하 암반의 열-수리-역학-화학적(thermal-hydrological-mechanical-chemical, THMC) 연계거동 해석기법 개발을 목표로 한다. DECOVALEX 프로젝트에서는 4년마다 새로운 주제에 대한 공동연구를 수행하게 되며, 각 참여기관은 각각의 수치해석 기법을 통해 현장시험과 실험실시험 등을 모사하는 방식으로 단계별 연구를 추진한다. 현재, 2016년에 DECOVALEX-2019가 착수되어 2019년까지 7가지 Task에 대한 공동연구를 수행할 예정이다. Table 1은 DECOVALEX-2019 프로젝트의 Task별 연구내용과 참여기관을 요약한 것으로, 참여기관은 향후 다소 변동될 가능성이 있다. 국내에서는 한국원자력연구원이 DECOVALEX- 2011과 DECOVALEX-2015에 이어 DECOVALEX-2019의 정식회원기관과 연구기관으로 참여하고 있으며, DECOVALEX-2019부터 한국지질자원연구원이 한국원자력연구원의 협력 연구기관으로 Task B를 수행하고 있다. 또한, 서울대학교가 스웨덴 원자력규제기관인 Swedish Radiation Safety Authority(SSM)의 협력 연구기관으로 참여하여 위탁연구를 수행하고 있다.
Table 1. Research organizations and tasks of DECOVALEX-2019
본 논문에서는 현재까지 한국지질자원연구원에서 수행한 Task B의 1단계 연구내용과 현황을 소개하였다. Task B의 정식명칭은 ‘Fault Slip Test: Modelling the induced slip of a fault in argillaceous rock’으로 단층 내 유체의 주입으로 인한 수리역학적 거동을 예측할 수 있는 해석모델을 개발하는 데에 최종목표가 있다. 본 연구에서는 1단계 연구인 벤치마크 모델(benchmark model)에 대한 3차원 수치해석을 수행하여 단층 내 유체 주입에 따른 수리-역학적 상호작용을 살펴보았다. 이를 위해 Rutqvist 외(2002)에 의해 제안된 TOUGH-FLAC 연동해석 기법을 이용하였으며, 두 가지 수리간극모델을 통해 단층과 주변 암반에서 발생하는 수리-역학적 거동을 살펴보았다. 이 과정에서 FLAC3D의 불연속 모델인 인터페이스 요소(interface element)를 사용하여 단층의 역학적 거동을 모사하였으며, 단층의 역학적 변형(간극의 변화)으로 인한 수리물성 변화와 기하학적 변화(해석 메쉬의 변형)를 수리해석에 반영할 수 있는 커플링 모듈을 개발해 TOUGH-FLAC 연동해석에 적용하였다.
2. 해석모델 개요
2.1 DECOVALEX-2019 Task B
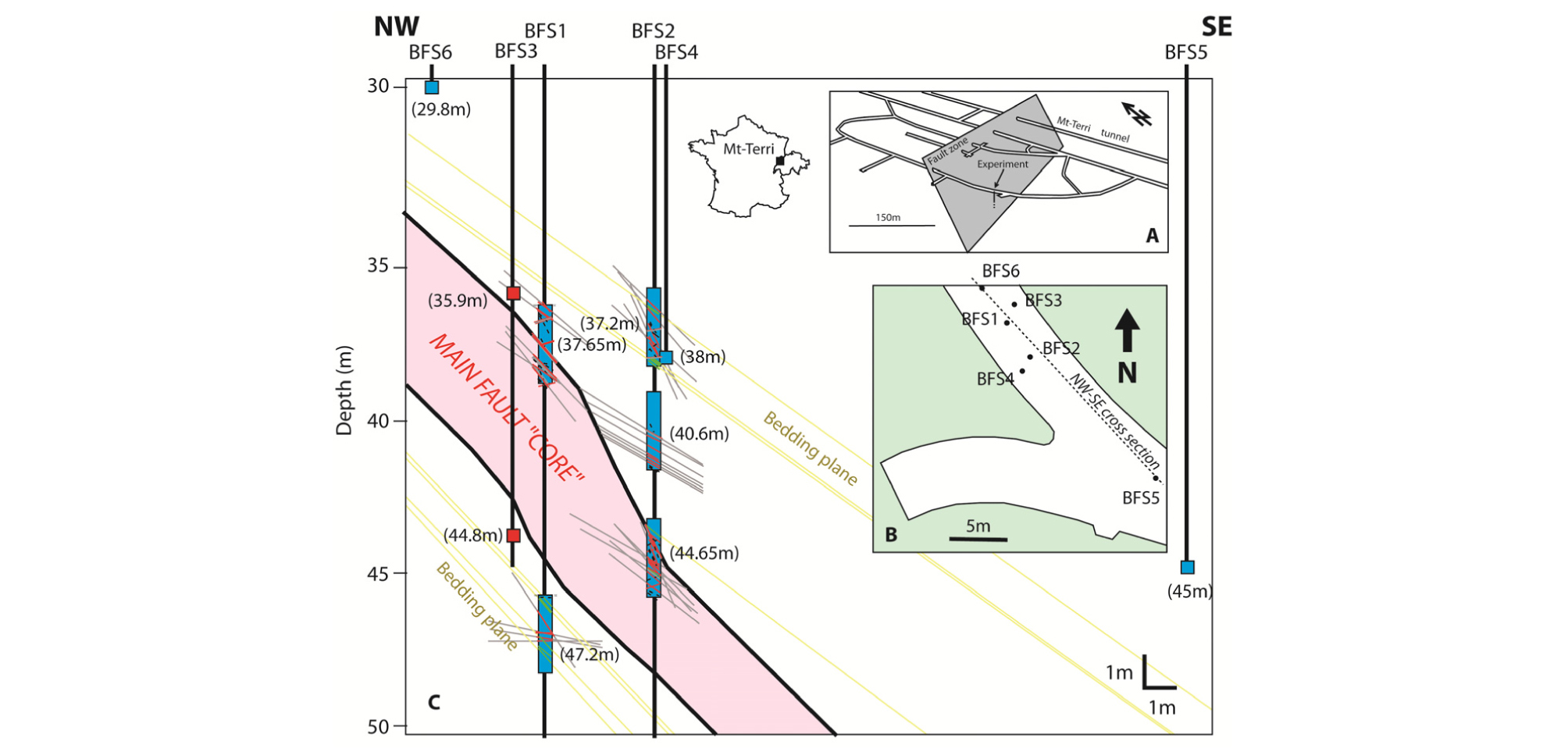
본 연구에서 수행하고 있는 Task B(Fault Slip Test: Modelling the induced slip of a fault in argillaceous rock)는 Swiss Federal Nuclear Safety Inspectorate(ENSI)이 제안하여, 한국지질자원연구원을 포함해 각국의 6개 연구팀이 참여하고 있다. Task B의 목표는 유체의 주입(유입)으로 인한 단층 활성화와 수리역학적 거동을 모사할 수 있는 수치모델을 개발하는 데에 있다. 향후 개발된 수치모델을 스위스 Mont Terri 지하연구시설(Underground Research Laboratory, URL)에서 수행된 ‘Fault activation experiment’ 현장시험(Fig. 1)에 적용하여 실측 결과와의 비교를 통해 그 타당성을 검증할 예정이다.
Task B의 추진일정은 2019년까지 크게 세 단계로 구성된다(Table 2). 1단계 연구는 벤치마크 시뮬레이션으로 각 연구팀들이 독자적인 해석 코드를 개발하고 모델링 기법을 수립하는 준비 단계의 연구라고 할 수 있다. 1단계 연구에서는 단순화된 단층 모델에 대한 해석 결과를 서면회의나 워크숍을 통해 상호 비교함으로써 개발된 해석코드를 지속적으로 개선할 수 있다. 2단계 연구(Step 2)와 3단계 연구(Step 3)는 각각 1단계에서 개발한 해석코드를 이용해 Mont Terri URL에서 수행된 ‘minor fault’와 ‘main fault’에 대한 주입시험을 모델링하는 단계이다. 이 단계에서는 현장의 조건과 시험 결과가 배포되며, 이를 바탕으로 개발된 해석기법을 검증할 수 있는 기회를 갖게 된다. 위 주입시험은 국제암반역학회(International Society for Rock Mechanics, ISRM)에서 제안한 시험법 중 하나인 Step-Rate Injection Method for Fracture In-situ Properties(SIMFIP)로, 단층이나 절리와 같은 불연속면에 다양한 압력의 물을 주입하여 선형/비선형 변형을 유도함으로써 불연속면의 역학적․수리적 물성을 측정하는 방법이다. 여러 현장의 절리와 단층을 대상으로 성공적으로 적용된 바 있으며, 양질의 반복성(repeatability)과 재현성(reproducibility)을 확보한 신뢰성 높은 시험 방법으로 알려져 있다(Guglielmi et al., 2014).
Table 2. Schedule for the different steps and reporting of TASK B
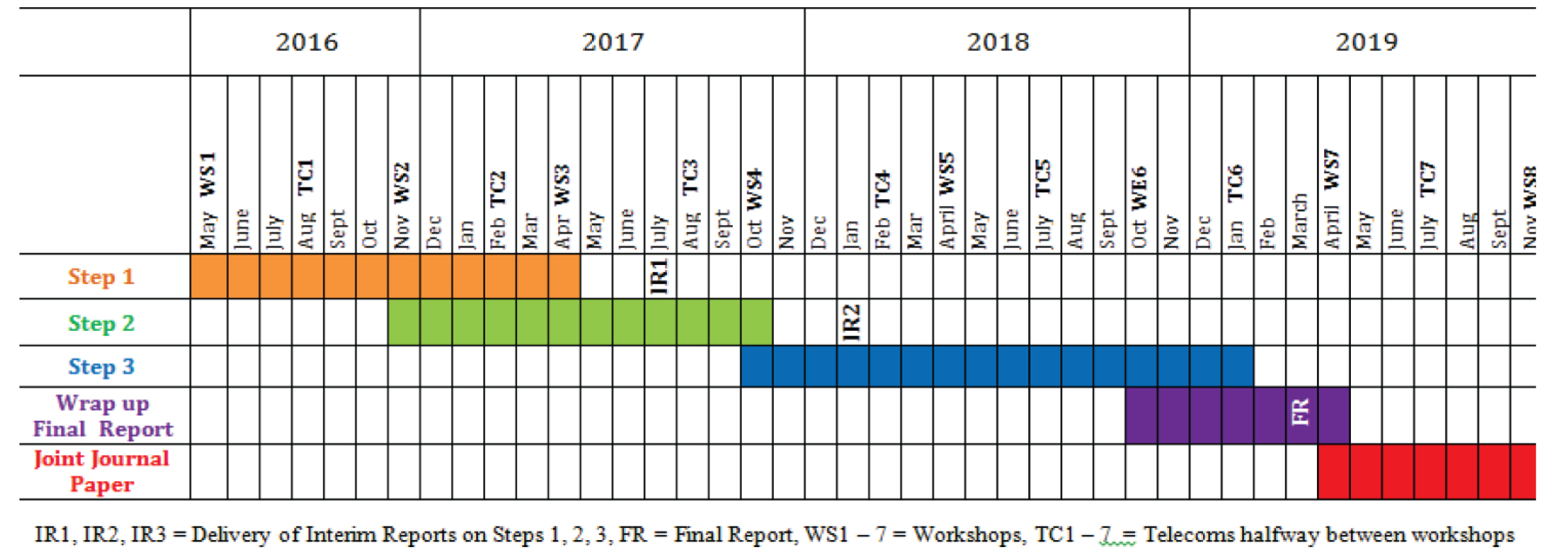 |
본 논문에서 소개하는 해석 결과는 1단계 연구내용으로, Table 2의 추진일정 중 2017년 4월 스웨덴 스톡홀롬에서 개최된 제3차 워크숍(WS3)에서 발표된 것이다. 당초계획에 따르면 2018년 8월 현재 2단계 연구가 종료되고 3단계 연구가 진행 중에 있어야 하나, 참가팀들의 연구진행이 지연되어 제4차 워크숍(WS4)까지 1단계 연구가 수행되었으며, 연구팀들의 해석 결과가 다소 큰 차이를 보여 원인규명을 위해 추가해석 필요성이 제기되었다. 현재, 1단계 연구의 추가해석과 2단계 연구가 진행 중에 있으며, 2018년 10월 한국에서 개최되는 제6차 워크숍에서 그 연구내용 및 결과가 논의될 예정이다.
2.2 Step 1: Benchmark test
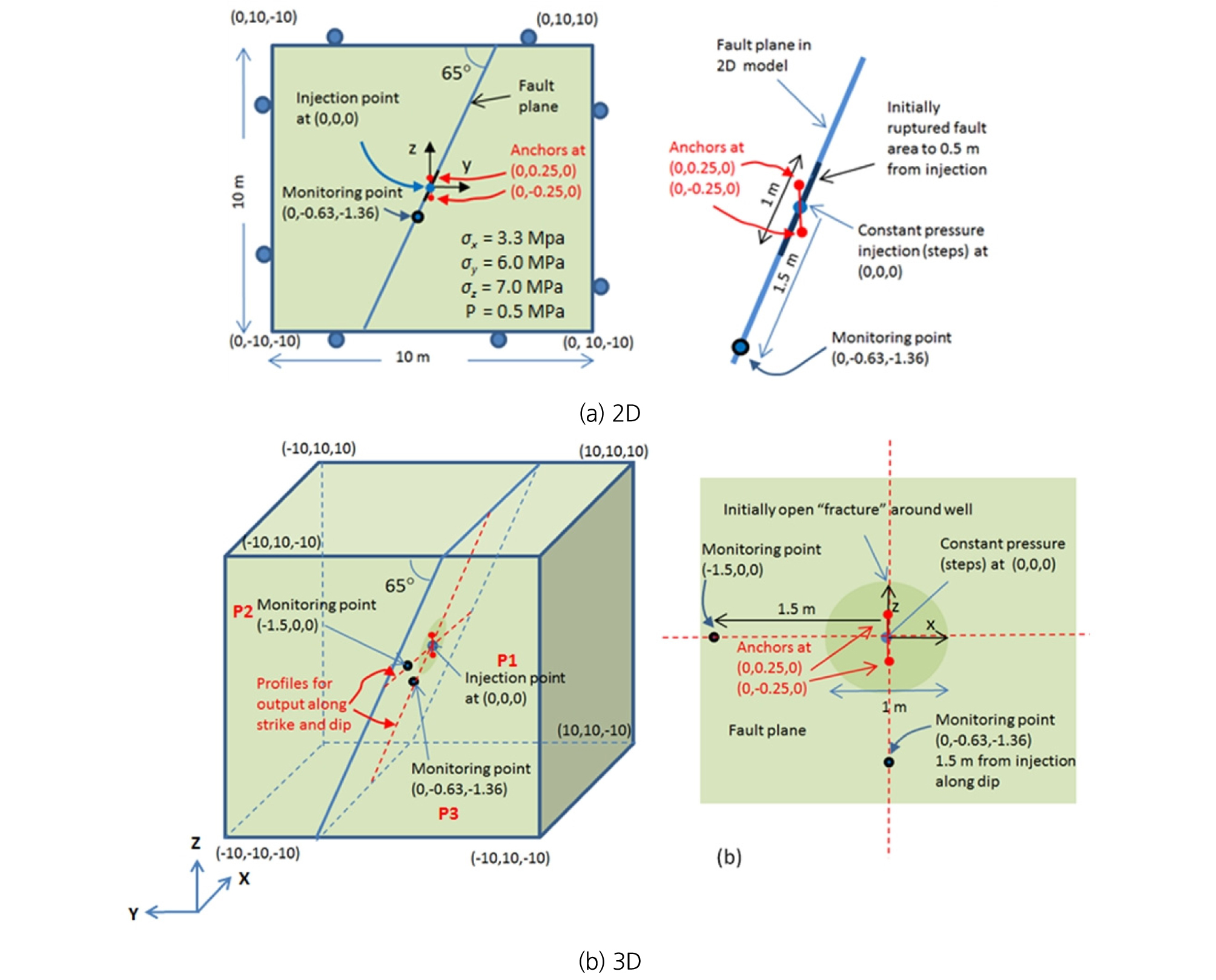
Fig. 2는 1단계 연구인 벤치마크 모델의 형상과 좌표계, 모니터링 지점 등의 정보를 보여준다. 각 참가팀은 2차원 또는 3차원 모델을 선택하여, 단층 주입시험을 모사하고, 단층과 주변 암반의 역학적 거동(변위, 응력, 파괴거동 등)과 단층의 수리 특성(유동경로, 수리간극, 투수계수, 압력분포, 유량 등)을 재현할 수 있는 수치해석 기법을 개발하게 된다.
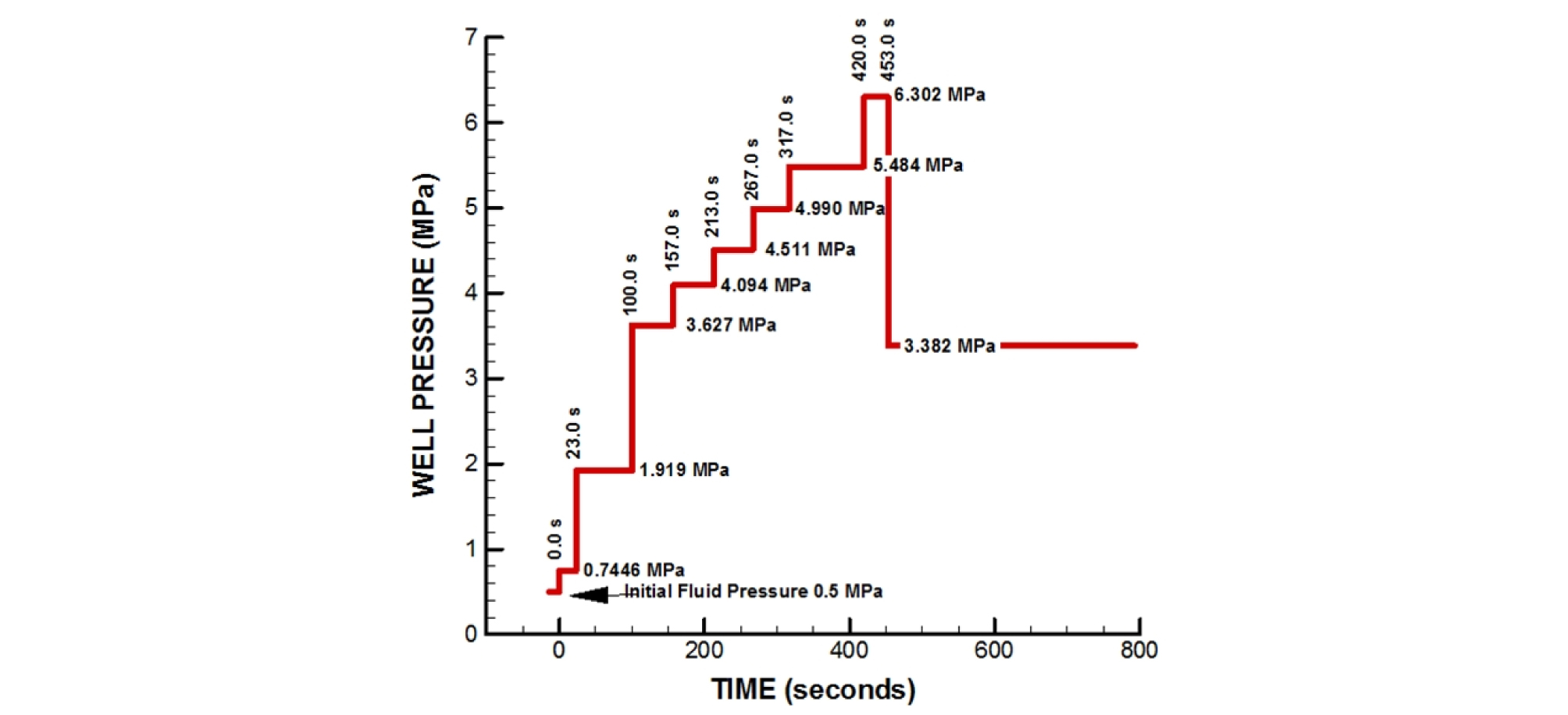
Fig. 3은 단층에 적용되는 주입압 조건을 보여주는 것으로 Mont Terri URL의 ‘minor fault’에 대한 현장주입시험 조건과 동일한 것이다. 주입과정은 총 9단계로 구성되는데, 각 주입단계에서는 일정한 주입압을 일정 시간 동안 유지하게 된다. 첫 번째 단계의 주입압은 0.7446 MPa이며, 여덟 번째 단계에서 최대 주입압인 6.302 MPa이 적용된다. 마지막 단계에서는 압력을 낮추어 354초 동안 3.382 MPa의 일정 주입압을 적용한다.
수리해석 시 암반은 불투수성으로 간주되고 주입수의 유동은 단층을 통해서만 이루어진다. 단층 내 유체의 흐름은 Darcy의 법칙을 따르며, 유량과 수리간극의 관계는 평행한 두 평판사이의 유체 흐름 모델인 삼승법칙(Witherspoon, 1980)을 따르는 것으로 가정한다. 즉, 수리간극(hydraulic aperture)이 bh이고 폭이 W인 단층을 통과하는 단위시간당 유량 Q는 다음과 같이 계산된다.
| $$Q=-W\frac{b_h^3\rho_fg}{12\mu}\frac{d\phi}{dx}$$ | (1) |
여기서 ρf는 유체의 밀도, g는 중력가속도이며, μ는 점성계수(dynamic viscosity), d∅/dx는 수두경사이다.
수리간극이 역학적 간극과 동일하다고 가정할 때, 수리간극의 크기는 다음과 같이 표현할 수 있다.
| $$b_h=b_{hi}+\bigtriangleup b_{he}+\bigtriangleup b_{hs}+\bigtriangleup b_{hc}$$ | (2) |
여기서 bhi는 초기 수리간극, ∆bhe는 단층의 수직방향 탄성변형에 의한 수직변위, ∆bhs와 ∆bhc는 단층의 전단파괴(미끄러짐 또는 활성화) 이후 발생하는 수직변위이다.
식 (1)을 변환하면, 단층의 투수계수 kf는 수리간극을 이용해 다음과 같이 계산할 수 있다.
| $$k_f=\frac{b_h^2}{12}$$ | (3) |
∆bhe는 단층의 수직강성 kn과 단층에 작용하는 유효 수직응력 변화량 ∆σbn′을 이용하여 식 (4)와 같이 계산할 수 있다.
| $$\triangle b_{he}=\triangle\sigma_n'/k_n$$ | (4) |
전통적인 암석역학에서는 전단파괴 이후 발생하는 간극의 변화를 단층면의 거칠기에 의한 수직팽창으로 간주하여 왔다. 식 (2)의 ∆bhs가 이에 해당되며, 전단변위 ∆us와 팽창각 ψ를 이용하면 다음과 같이 수식화할 수 있다.
| $$\bigtriangleup b_{hs}=\bigtriangleup u_s\times\tan\psi$$ | (5) |
그러나 Guglielmi 외(2015)는 프랑스 Tournemire URL에서 수행된 단층 주입시험 및 이에 대한 수치해석 결과를 토대로, 식 (4)의 수직팽창 모델이 현장시험에서 파괴 이후 발생한 간극의 변화량을 과소평가한다고 보고하였다. 그들은 이를 해결하기 위하여 전단 또는 인장파괴 시 일정량의 수직팽창이 발생하는 모델을 제안하였으며, 식 (2)의 ∆bhc가 이에 해당하는 값이다. Task B에서는 ∆bhc를 ‘creation aperture at rupture’로 지칭하고 ∆bhs(fracture opening by shear dilation)와 구별하여 사용하고 있다.
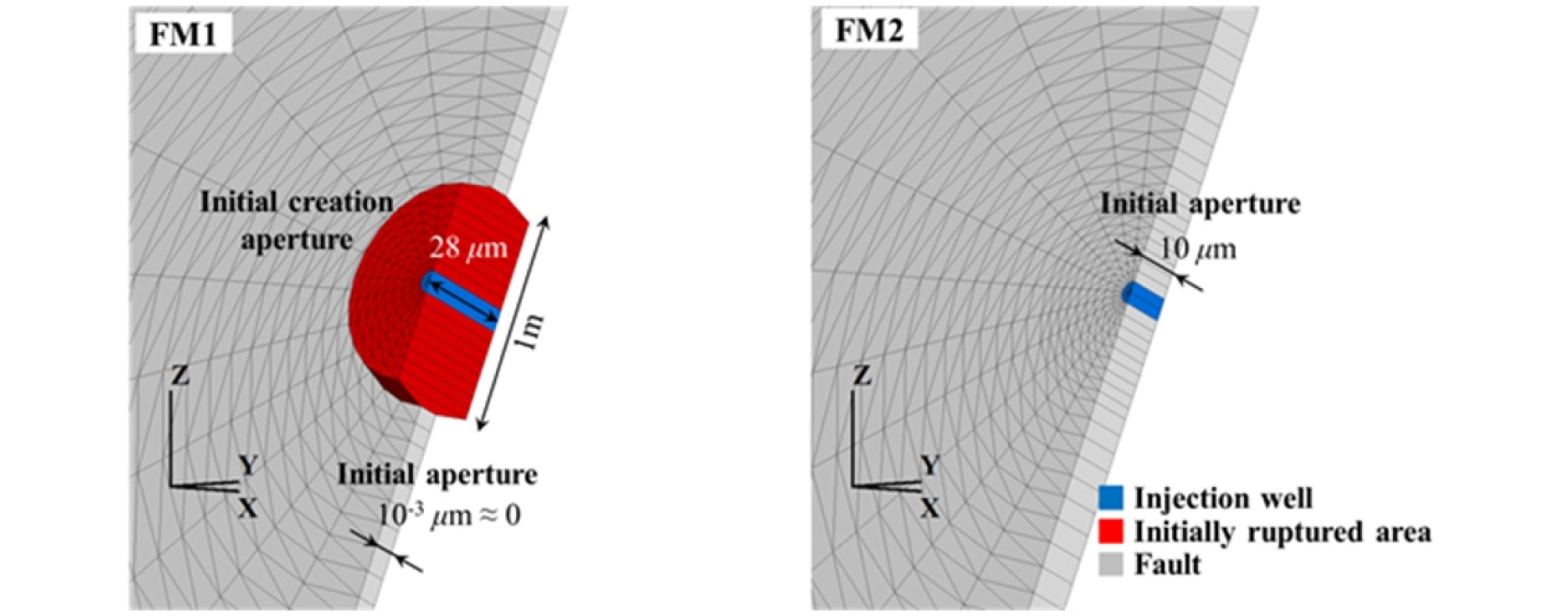
벤치마크 시뮬레이션에서는 두 가지 수리간극모델(FM1, FM2)을 사용한 수치해석이 제안되었으며, 각 수리간극모델의 특징은 다음과 같이 요약할 수 있다. FM1 모델에서는 초기 수리간극과 팽창각을 모두 0으로 가정한다. 단층은 전단파괴 발생 이전에는 탄성적으로 거동하며, 파괴 이후에는 일정량의 수직팽창(creation aperture, 28.0 μm)에 의해 수리간극이 증가한다. 주입지점으로부터 1.0 m 직경 이내의 영역은 주입 전에 이미 파괴된 상태(수리간극: 28.0 μm)로 가정하며 나머지 영역에서 불투수층이다. 한편, FM2 모델에서는 단층의 초기 수리간극이 10 μm이며, 팽창각은 10.0°이다. 전단파괴 이전에는 탄성적으로 거동하며, 이후에는 팽창각에 의해 수리간극이 증가한다. 파괴 후 발생하는 일정량의 수직팽창은 고려하지 않는다.
Table 3은 수치해석에 사용된 단층과 암반의 역학적 물성 및 주입 유체의 수리적 물성을 나열한 것이다. 단층과 암반의 역학적 물성은 스위스 Mont Terri URL에서 수행된 부지조사 결과를 통해 결정된 값으로 현지의 단층과 모암인 ‘minor fault’와 Opalinus Clay의 물성이다.
Table 3. Material properties for Step 1 benchmark simulations
2.3 TOUGH-FLAC 연동해석
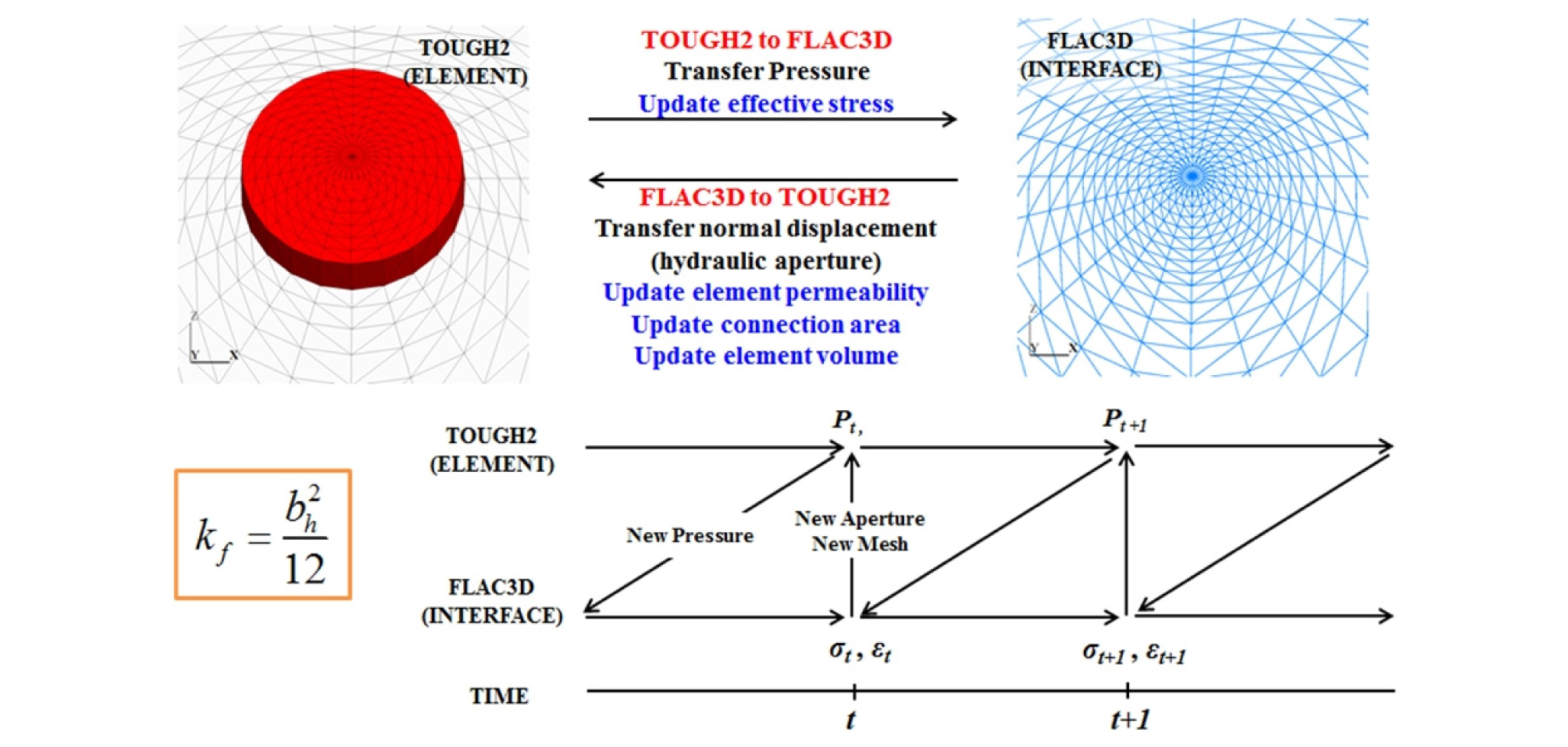
TOUGH-FLAC 연동해석 기법은 Rutqvist et al.(2002)이 개발한 해석기법으로 현재까지 방사성폐기물 처분, CO2 지중저장, 심부지열개발, 압축공기에너지저장, 열에너지저장 등 다양한 암반공학 문제에 적용되어 왔다(Rutqvist, 2012, Ruqvist & Tsang, 2012, Tsang et al., 2008, Rutqvist et al., 2015, Kim et al., 2012, Park et al., 2016). 이는 다상(multi-phase), 다성분(multi- component)의 유체유동/열유동 코드인 TOUGH2와 암반 및 지반의 역학적 거동 해석프로그램인 FLAC3D를 연동하는 방법으로서 구성방정식을 통한 커플링이 아닌 두 프로그램간의 해석 결과 교환을 통한 연성해석이라고 할 수 있다. 두 프로그램간의 연동은 TOUGH2의 비선형 반복계산(열-수리 유동해석)과 FLAC3D의 준정적 해석(역학적 거동해석)을 순차적으로 반복하는 방식으로 이루어지며, 두 프로그램의 해석 결과는 각각 TOUGH2 코드에 추가된 별도의 subroutine과 FLAC3D 내의 FISH 함수를 통해 구축된 연계 모듈을 통해 상호 교환된다. 이 과정에서 FLAC3D는 TOUGH2에서 계산된 열-수리적 해석 결과(온도, 압력 등)를 입력받아 역학적 거동을 계산하게 된다.
Cappa와 Rutqvist(2011)는 TOUGH-FLAC 시뮬레이터를 이용한 지층 내 이산화탄소 주입 모델링 연구에서 단층의 역학적 거동을 모사하기 위한 세 가지 방법을 제시하였다: 1) 두께가 없는 불연속 인터페이스 모델(zero-thickness mechanical interface), 2) 유한한 두께의 등가연속체 모델(equivalent continuum model using solid element), 3) 연약면을 포함한 유한한 두께의 등가연속체 모델(combination of solid elements and ubiquitous-joints oriented as weak planes). FLAC3D에서 인터페이스는 불연속면을 모사하기 위한 해석 요소로, 연속체 요소들 간 경계면에 인터페이스 요소를 할당하면 전단/수직방향의 구성방정식과 강도정수 등을 통해 단층의 미끄러짐(slip)과 분리(separation)를 재현할 수 있다. 등가연속체 모델은 단층을 연속체 모델의 일부 영역으로 설정하는 방법이다. 일반적인 암반공학 문제에서 단층의 수리간극은 연장이나 폭에 비해 매우 작기 때문에, 연속체 모델을 이용하는 경우 해석요소의 불량한 종횡비 문제를 해결하기 위해 실제보다 더 큰 간극 두께를 가정하게 된다. 따라서 단층 물성(강성, 강도, 수리간극 등)을 해석요소 두께에 상응하는 등가물성(변형계수, 강도, 투수계수 등)으로 변환하여 입력 자료로 사용하게 되며, 결과 분석 시에도 변형률을 통해 단층의 변위를 역산해야한다는 단점이 있다. 유비쿼터스 조인트(ubiquitous joint) 모델은 연속체 요소 내에 단층과 평행한 연약면을 설정하는 방법으로 미끄러짐이나 분리를 모사할 수는 없지만, 단층(연약면)의 방향에 따라 파괴를 유도할 수 있다. Cappa와 Rutqvist는 주입공과 인접한 단층에서 압력, 유효 수직응력, 전단응력, 전단변위를 비교한 결과, 세 모델이 유사한 해석 결과를 보이며, 단층 모델링 시 작업이 용이한 등가연속체를 사용하여도 무방하다고 보고하였다. 그러나 그들의 해석에서는 단층의 변형이 수리해석에 영향을 미치지 않으며, TOUGH2에서 계산된 압력만이 FLAC3D의 유효응력 해석에 영향을 미치는 일방향 연동해석(one-way coupling)이 수행되었다. 즉, 단층의 수리간극이 변화하지 않는다는 가정을 전제한다. 따라서 위 해석 결과는 세 단층 모델을 이용하여 동일한 유효응력(압력) 조건에서 동일한 역학적 거동을 재현하였다는 점에서는 유의미하나, 수리간극의 변화가 수리해석 결과에 반영되는 쌍방향 연동해석(two-way coupling)에서도 동일한 결론을 얻을 수 있을지에 대해서는 확신하기 어렵다.
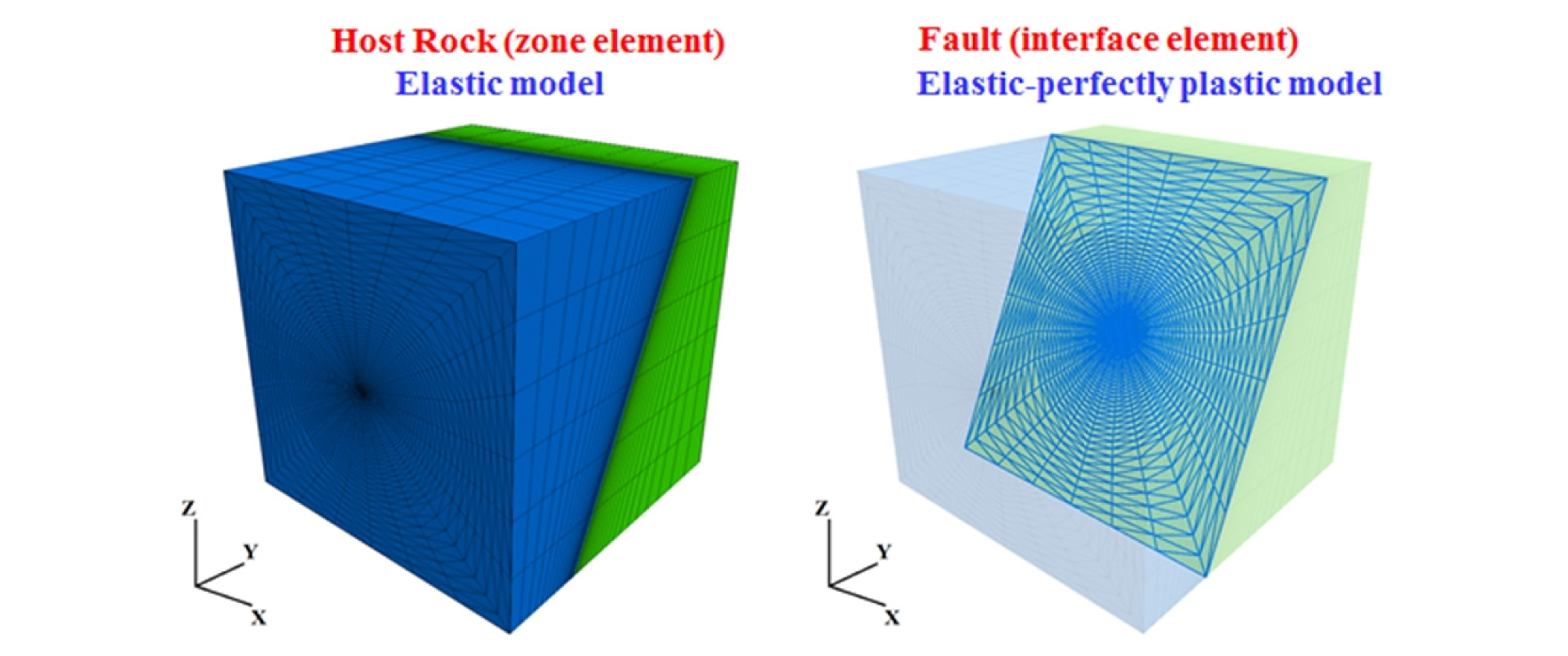
본 연구의 벤치마크 시뮬레이션에서는 단층으로 직접적인 물 주입이 이루어지고, 수리간극의 변화와 유동경로의 확산을 정확히 예측하는 것이 핵심 연구내용이다. 연속체 해석을 사용하는 경우, 단층의 수리간극을 역추산해야 할 뿐만 아니라 수리간극 변화를 지속적으로 등가 투수계수로 변환하는 과정에서 지나친 가정의 중첩이 발생할 것으로 판단되었다. 따라서 본 연구에서는 모델링 과정이 복잡하지만, 단층의 거동을 직접적으로 재현할 수 있는 인터페이스 요소를 이용하였다. 본 연구에서는 3차원 모델에 대한 수치해석을 수행하였으며, Fig. 4는 FLAC3D에서 작성된 해석모델의 형상을 보여준다. 단층과 암반의 입력 파라미터는 Table 3에 나열한 바와 같다. 암반은 탄성 모델이며, 단층은 탄소성 모델인 Coulomb sliding 모델을 따른다.
역학적 거동해석이 수행되는 FLAC3D의 경우, 암반의 탄성적 거동이 단층의 응력과 변위에 복합적인 영향을 미치게 되므로 전체 영역에 대한 해석 메쉬(mesh)가 필요하지만, 수리해석에서는 암반을 불투수층으로 가정하므로 TOUGH2 해석 시 단층에 대한 메쉬만을 작성하였다. 두 프로그램의 연동해석 시 데이터의 교환은 TOUGH2의 전체 요소와 FLAC3D의 인터페이스 요소 사이에서 이루어진다.
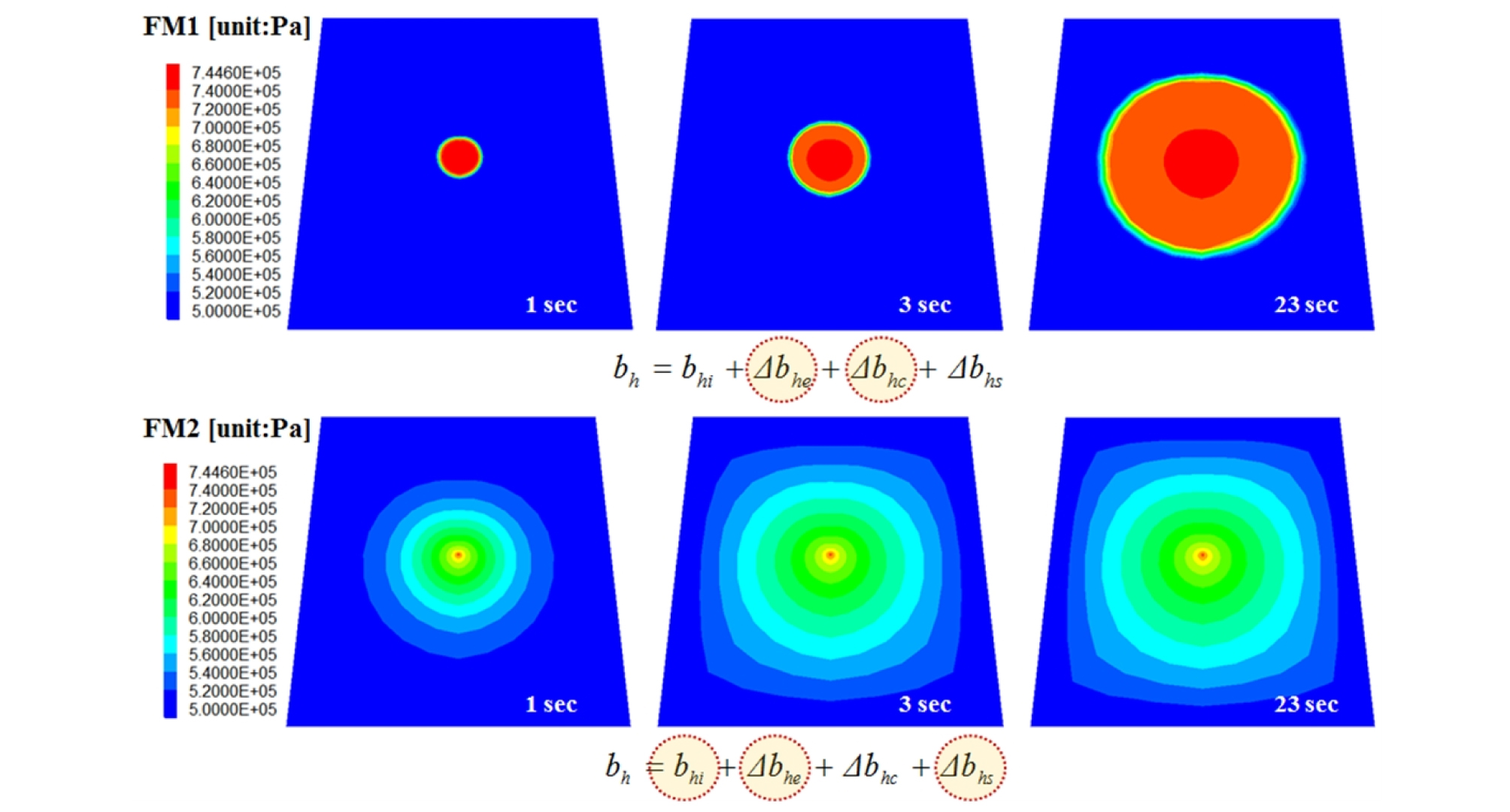
Fig. 5는 TOUGH2 해석에 사용된 FM1 수리간극모델과 FM2 수리간극모델의 초기 해석메쉬를 보여주는 것으로, 주입정 주변의 단층 단면을 보여준다. FLAC3D에서 인터페이스 요소는 두께가 없는 가상의 불연속면이지만, TOUGH2의 각 요소는 수리간극 크기에 상응하는 두께를 갖는다. 독자의 이해를 돕기 위해 Fig. 5에는 수리간극의 크기를 임의로 확대하여 표시하였다. FM1 모델의 경우, 주입공으로부터 1.0 m 직경 이내에서는 이미 파쇄된 상태를 가정하며, 28.0 μm의 수리간극(creation aperture)을 갖는다. 나머지 영역에서는 초기 수리간극이 0이지만, 잠재적인 유동경로로서 수리해석에 반영될 부분이므로 0에 가까운 얇은 두께(10-3μm)를 설정하였다(수리간극(수직변위)의 변화가 없으면 수리해석 시 비활성 요소로 처리된다). FM2 모델은 모든 영역에서 초기 수리간극이 10 μm이다.
Fig. 5를 초기 해석메쉬라고 지칭하는 이유는 해석이 진행됨에 따라 TOUGH2 해석 메쉬의 정보가 지속적으로 업데이트되기 때문이다. TOUGH-FLAC 시뮬레이터를 이용한 선행연구들에서는 대부분 등가연속체 모델을 이용해 유효응력으로 인한 공극율, 투수계수, 모세관압 등 수리적 물성의 변화에 초점을 맞추고 있다. 그러나 벤치마크 모델의 경우, 단층의 영역별로 초기 수리간극이 다르거나, 전단파괴 시 갑작스러운 수리간극의 변화가 예상되었으므로, 수리해석 시 보다 정확한 유량과 압력 해석을 위해 단층의 기하학적 변화(해석 메쉬의 변형)를 반영할 필요가 있었다.
따라서 FLAC3D 인터페이스의 변위 해석 결과를 토대로 TOUGH2 요소들의 메쉬 정보와 투수계수를 동시에 업데이트할 수 있는 별도의 subroutine을 개발하였으며, 이를 TOUGH-FLAC 연동해석에 반영하였다. Fig. 6은 TOUGH2와 FLAC3D 프로그램 간의 연동해석 과정을 보여주는 것으로, 두 프로그램의 호출(실행)과 데이터 교환은 TOUGH2의 Newton iteration level에서 매 time step마다 순차적으로 반복된다. TOUGH2에서 각 해석 요소의 압력을 계산하여 FLAC3D로 전송하면, FLAC3D에서는 인터페이스 절점의 압력을 업데이트하여 유효응력 기반의 준정적 해석을 수행한다. 계산된 인터페이스 절점의 수직변위(수리간극)는 다시 TOUGH2로 전송되어 각 해석 요소의 수리간극, 투수계수, 메쉬 정보를 업데이트하고, TOUGH2는 다음 time step의 수리해석을 수행한다. 이때 TOUGH2는 요소의 부피 중심에서의 해석 결과를, FLAC3D는 인터페이스의 각 절점에서의 해석 결과를 출력하게 되므로 두 프로그램 간의 데이터 교환을 위한 데이터 변환이 필요하였으며, 본 연구에서는 이를 위해 역거리가중법(inverse-distance weighting)을 이용하였다. 여기서 가중치는 인접한 요소의 중심 또는 인터페이스 절점의 좌표정보를 이용하여 거리 제곱에 반비례하는 것으로 가정하였다.
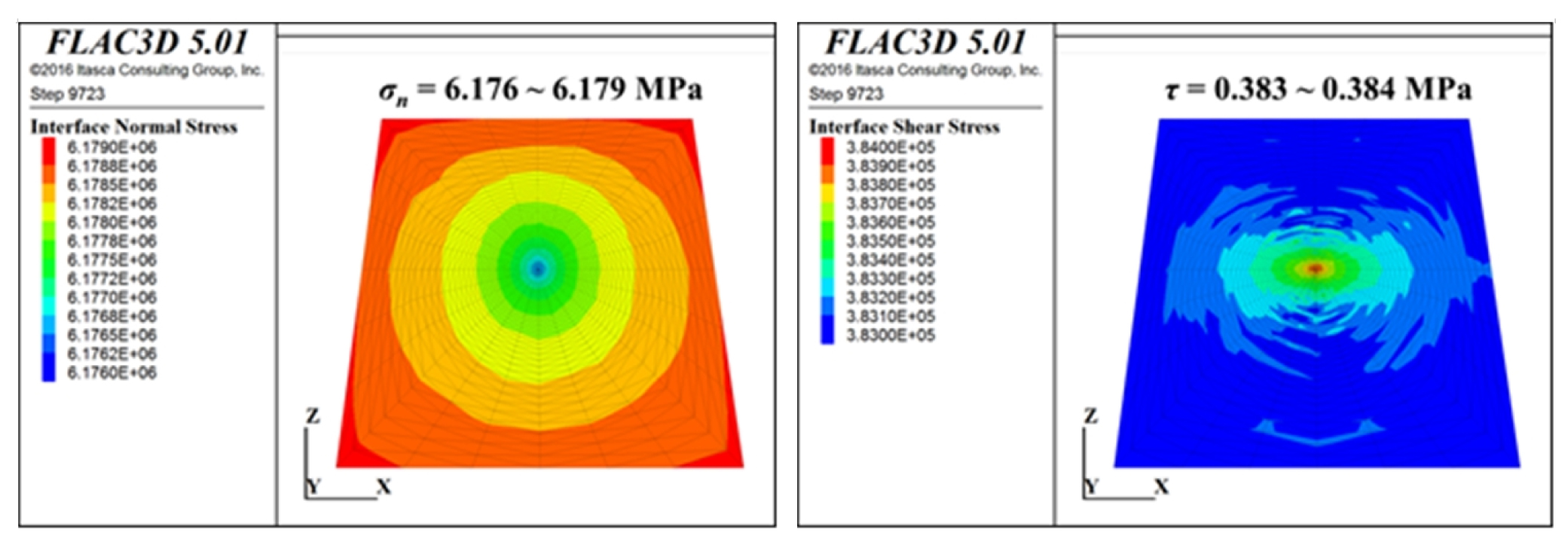
벤치마크 모델의 현지응력 조건은 σx= 3.3 MPa, σy= 6.0 MPa, σz= 7.0 MPa이며, 초기압력은 0.5 MPa이다(좌표계: Fig. 2 참조). 해석모델의 경계에서는 각 면의 수직방향으로 변위가 구속되고 0.5 MPa의 압력이 일정하게 유지된다. Fig. 7은 위 조건을 바탕으로 구현된, 인터페이스 요소(단층)에 작용하는 초기 전단응력과 초기 수직응력을 보여주는 것으로 범례(legend)의 단위는 Pa이다.
단층의 주향방향으로 작용하는 주응력 σx는 단층에 수직응력과 전단응력을 유발하지 않으므로 65° 경사의 단층에 작용하는 수직응력과 전단응력은 식 (6)과 같이 이론적으로 계산할 수 있다. Fig. 7의 해석 결과와 식 (6)의 이론해를 비교하면, 단층의 초기응력 상태가 적절히 재현되었음을 확인할 수 있다.
3. 해석 결과 및 토의
Task B의 각 참가팀은 두 수리간극모델에 대한 주입시험을 수행하고 다음의 해석 결과를 제출하여야 한다. 주입 지점, 모니터링 지점, 프로파일 위치 등은 Fig. 2에 표시된 바와 같다.
1) 주입지점 P1(0, 0, 0)에서의 물 주입율(injection flow rate): P1의 위치는 해석모델과 단층의 중심
2) 상반 앵커(0, 0, 0.25)와 하반 앵커(0, 0, -0.25) 간의 상대변위(dx, dy, dz): 상반과 하반의 앵커는 주입지점에서 수직방향으로 각각 0.25 m 이격
3) 주입지점 P1에서의 수직변위(수리간극), 경사방향 전단변위, 주향방향 전단변위
4) 모니터링 지점 P2(-1.5, 0, 0)에서의 수직변위, 경사방향 전단변위, 주향방향 전단변위: P2의 위치는 P1으로부터 주향방향으로 1.5 m 이격
5) 모니터링 지점 P3(0, -0.63, -1.36)에서의 수직변위, 경사방향 전단변위, 주향방향 전단변위: P3의 위치는 P1으로부터 경사방향으로 1.5 m 이격
6) 모니터링 지점 P2에서의 압력
7) 모니터링 지점 P3에서의 압력
8) 주입 후 317초, 주입 후 807초 경과 시, 주입지점을 통과하는 주향방향 프로파일을 따르는 압력, 수직변위
Fig. 8 ~ Fig.19는 상기 제출결과를 포함한 해석 결과를 보여주는 것으로, 본 논문에서는 결과 분석 및 논의를 위해 여러 해석 결과를 통합적으로 제시하거나 기타 유의미한 정보를 추가로 도시하였다.
3.1 역학적 거동
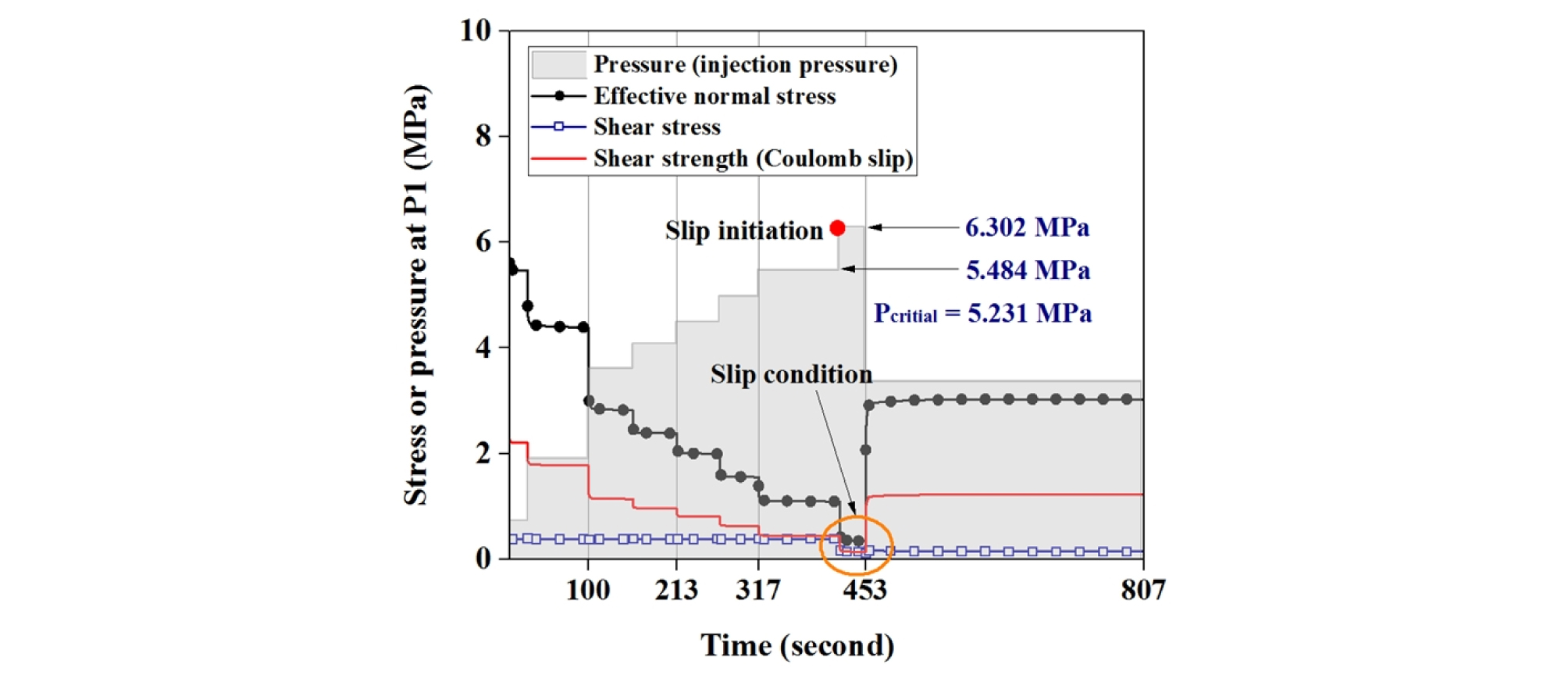
Fig. 8은 FM1 수리간극모델의 해석 결과로 주입지점 P1에서 측정된 압력, 유효수직응력, 전단응력, 전단강도의 변화를 보여준다. 여기서 전단강도는 유효수직응력 해석 결과와 단층의 강도(마찰각, 점착력)를 이용해 이론적으로 계산된 Coulomb sliding 모델의 전단강도이다. FLAC3D의 인터페이스 절점에서는 전단응력이 전단강도를 초과할 때 전단파괴(미끄러짐)가 발생하고, 이후의 전단응력은 파괴 시 전단응력과 동일하게 유지되는 것을 가정한다. 전단응력 곡선을 살펴보면, 420초를 전후로 전단강도에 도달하였고 전단파괴가 발생한 이후 전단응력이 일정한 값을 유지하고 있음을 확인할 수 있다. 유효 수직응력은 계단식으로 감소하였고, 주입압이 낮아지는 453초 이후에 다시 증가하였다. 단층의 미끄러짐을 유발할 수 있는 이론적인 최소압력(critical injection pressure, Pcrit)은 Coulomb sliding 모델의 파괴기준 및 식 (6)의 수직응력과 전단응력을 이용해 다음과 같이 추정할 수 있다.
| $$P_{crit}=\sigma_n-\frac{(\tau-c)}{\tan\phi}=5.231MPa$$ | (7) |
수치해석에서는 식 (7)의 압력보다 높은 주입압인 5.484 MPa가 적용되었을 때(317~420초)에도 전단파괴가 관찰되지 않았으며, 주입압이 6.302 MPa인 420~453초 사이에 전단파괴가 발생하였다. 벤치마크 모델의 경우, 물 주입 이외의 외적 변화요인이 작용하지 않으므로 유효 수직응력과 압력의 합인 전응력(total normal stress)이 이론적으로 일정하여야 한다. 즉, 압력의 증가량은 유효수직응력의 감소량과 동일할 것으로 기대할 수 있다. 그러나 수치해석에서는 단층의 수직변위와 암반의 탄성거동으로 인해 유효수직응력의 증분이 발생하였고, 이에 따라 압력 증가량에 비하여 유효수직응력 감소량이 적었다. 따라서 전단강도가 예상보다 높게 발현되었고, 주입압이 6.302 MPa이 되었을 때 비로소 전단파괴가 발생한 것을 확인할 수 있었다. FM2 수리간극모델의 해석 결과도 자세한 수치의 차이는 있으나, 전반적으로 대동소이한 경향을 보였다.
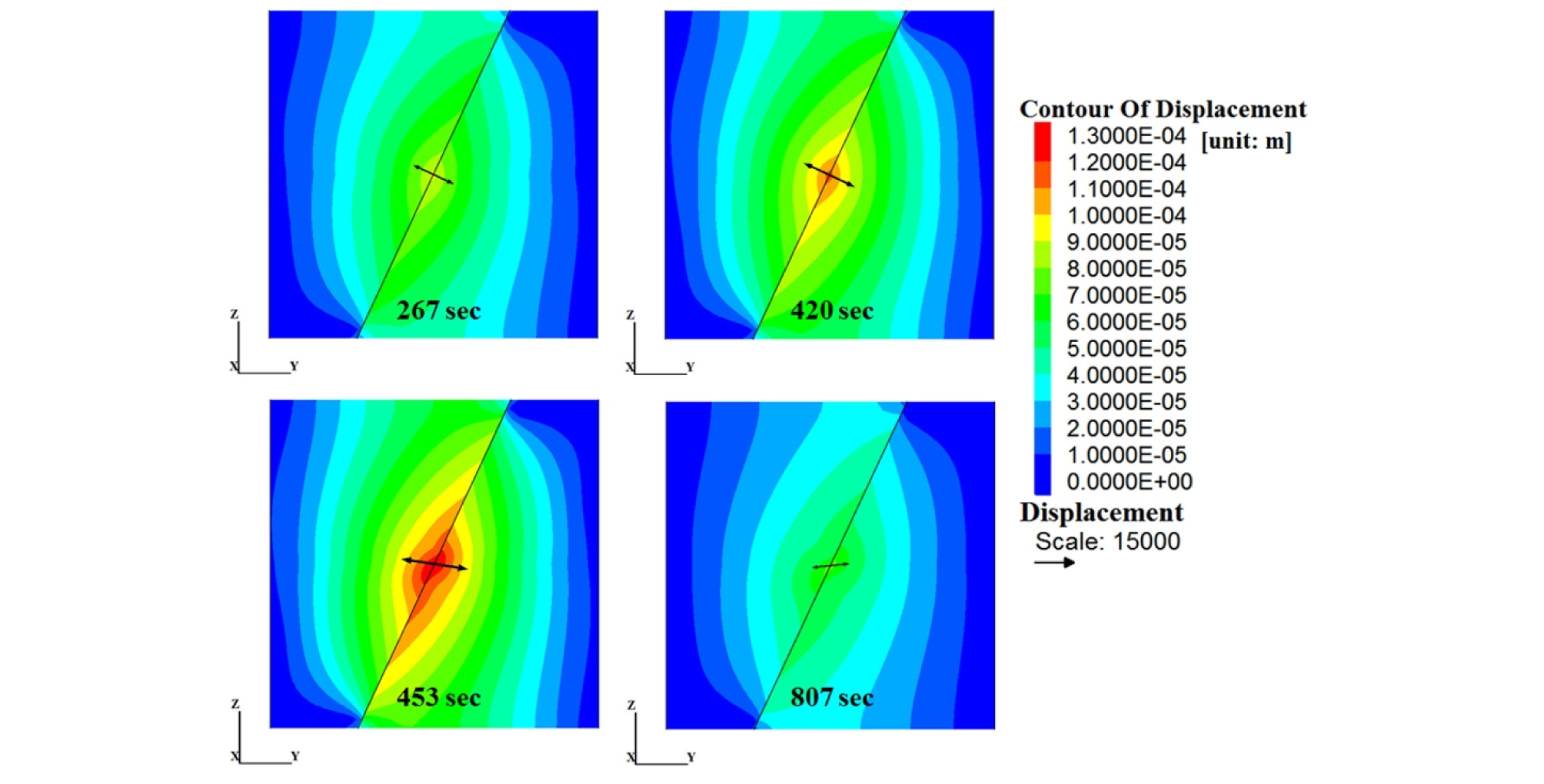
Fig. 9는 FM1 수리간극모델의 주입 후 267, 420, 453, 807초 경과 시의 해석 결과로 주입지점을 지나는 YZ 평면(수직단면)에 암반 변위(스칼라)를 도시한 것이다. 화살표는 주입지점에서의 인터페이스 변위를 15,000배 스케일로 표현한 벡터이다. 주향방향(X축 방향) 변위는 해석모델의 대칭성으로 인해 ± 0.1 μm 범위의 무시할 수 있는 수준으로 나타났다. 변위 벡터의 방향을 살펴보면, 전단파괴가 개시된 420초 이전에는 수직방향 팽창이 두드러지며 420초 이후 상반이 하반을 타고 아래로 미끄러지는 정단층의 거동을 보였다. 주입압이 다시 낮아지는 453초 이후에는 단층의 전단변위는 더 이상 증가하지 않았고, 탄성적인 수직변위만이 회복되었다.
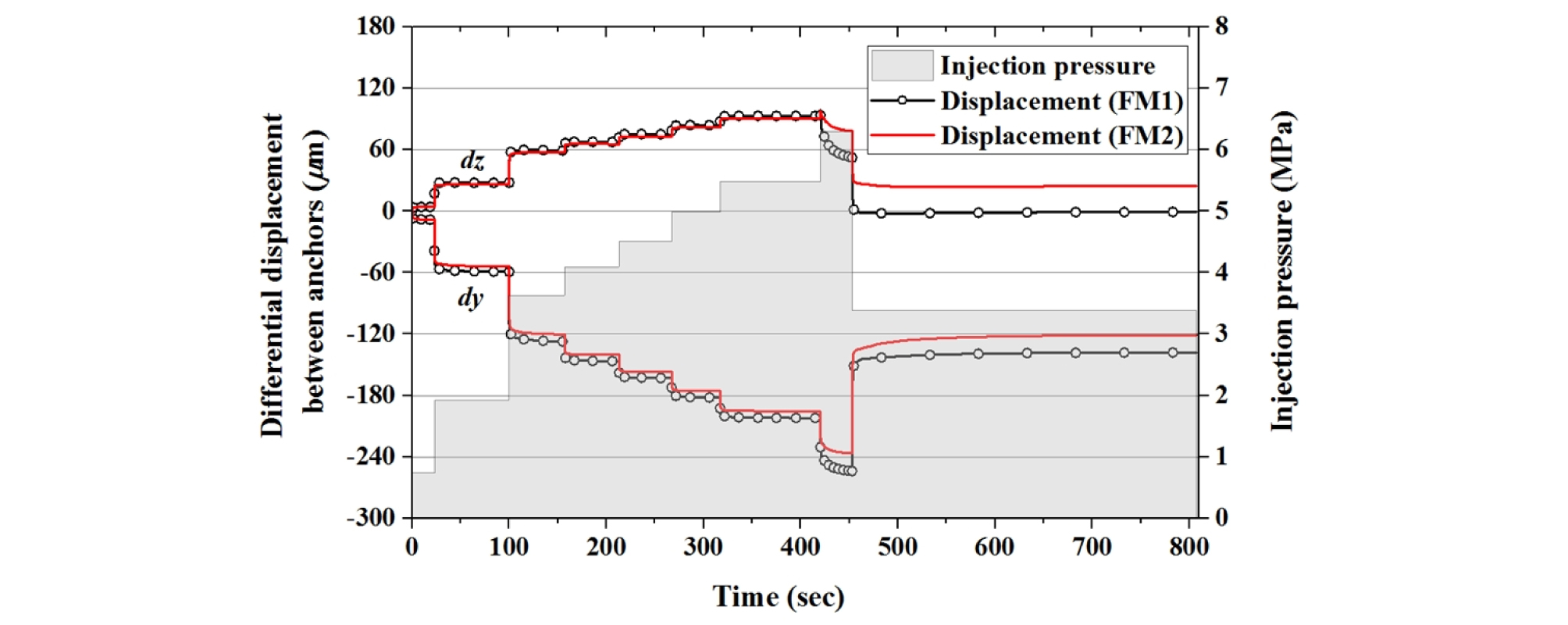
Fig. 10은 두 수리간극모델에 대한 해석 결과를 비교하여 도시한 것으로 상반 앵커와 하반 앵커의 상대변위(dy, dz)를 보여준다. 두 앵커는 주입지점의 수직방향으로 0.5 m 거리에 위치한다. 해석모델의 대칭성으로 인해 X축 방향의 상대변위(dx)는 ±0.1 μm 범위의 미미한 수치를 보였다. Fig. 10의 변위를 Fig. 9의 암반 변위와 개략적으로 비교하면, 전자가 후자의 약 2배 스케일을 가지는 것을 알 수 있는데, 이는 전자가 하반 앵커에 대한 상반 앵커의 상대변위를 의미하는 반면, 후자는 암반 내 한 지점에서의 절대변위를 의미하기 때문이다. 좌표축과 상대변위의 방향을 고려하여 살펴보면, 전단파괴 이전에는 두 수리간극모델이 유사한 거동을 보이지만 420초 이후에는 FM1 모델에서 단층의 미끄러짐이 더욱 두드러짐을 확인할 수 있다.
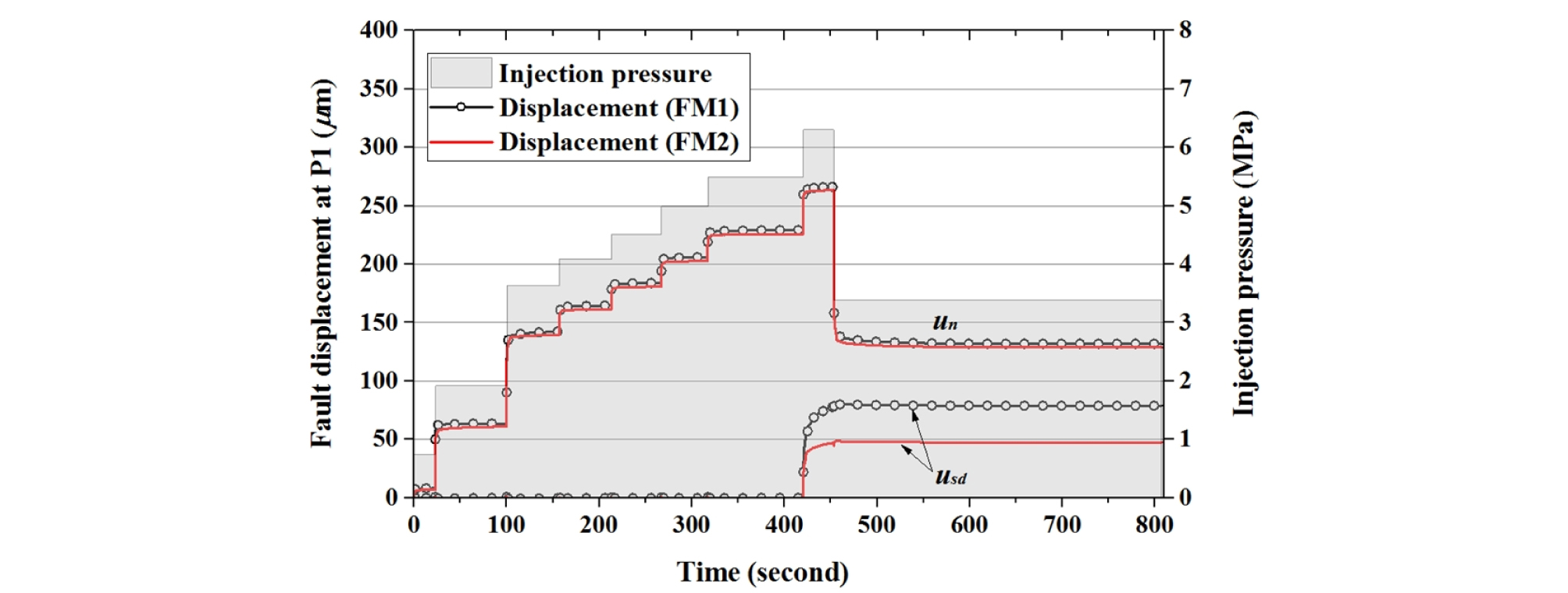
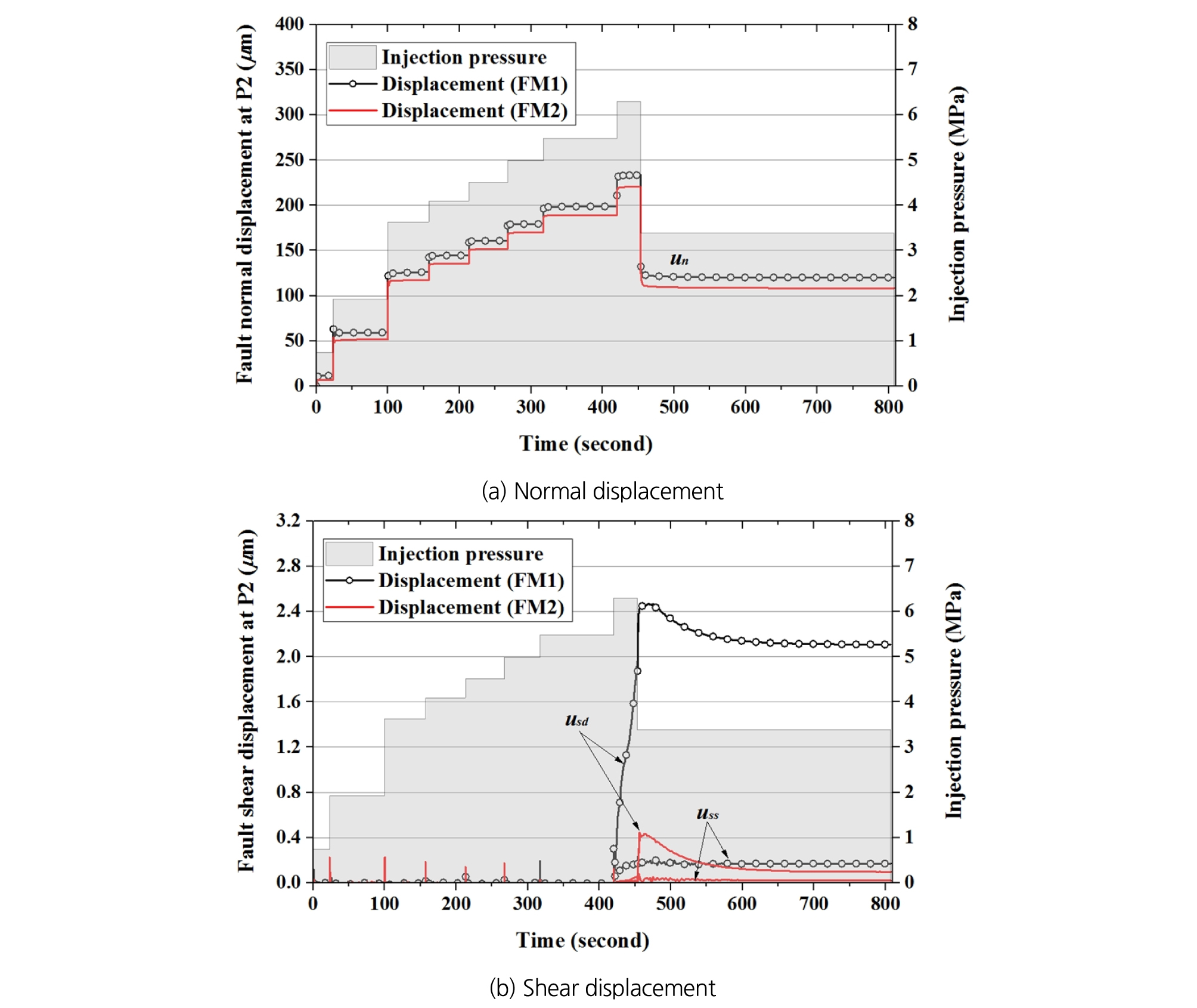
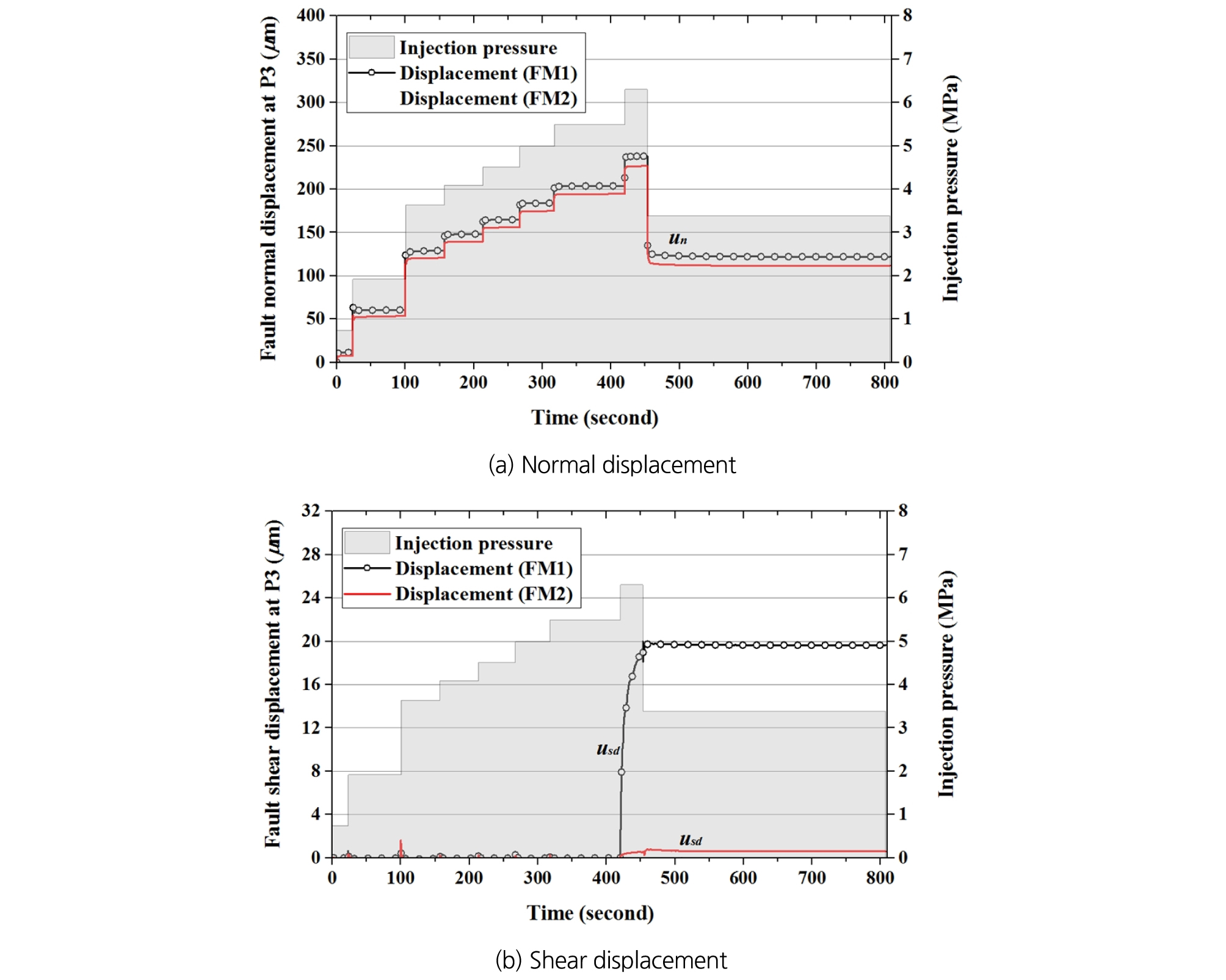
Fig. 11~Fig. 13은 주입지점(P1)과 모니터링 지점(P2, P3)에 측정된 단층의 수직변위(un), 경사방향 전단변위(usd), 주향방향 전단변위(uss)를 보여준다. 모니터링 지점 P2와 P3는 단층면 상에 위치하며, 각각 주향방향과 경사방향으로 주입지점에서 1.5 m 이격거리에 위치한다. P1, P3 지점에서는 주향방향 전단변위(uss)가 ± 0.1μm 범위의 낮은 수치를 보였으며, P2 지점에서는 주향방향으로도 유의미한 전단변위가 관찰되어 Fig. 12b에 함께 도시하였다.
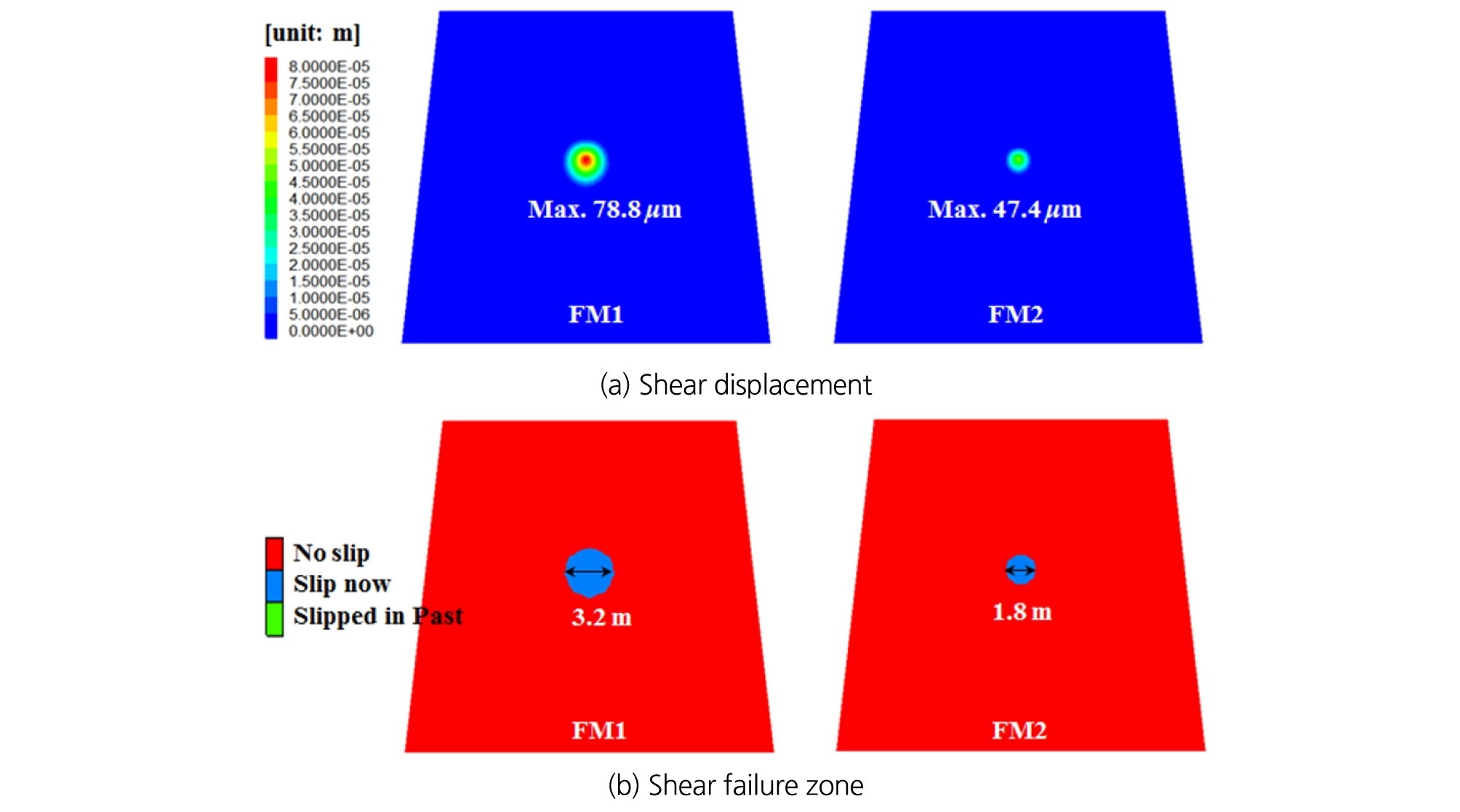
P1에서 단층의 수직변위는 두 모델에서 유사한 수치를 보이는 것으로 나타났으며, 주입압에 비례하여 계단식으로 변화하는 경향을 보였다. 각 단계에서 주입압을 적용한 후 수 초 이내에 수직변위가 즉각적으로 발생하였으며, 453초 이후에는 유효수직응력이 증가하면서 수직변위가 감소하였다. 420~453초 사이에 단층의 경사방향으로 전단변위가 발생하였고, 주입압이 감소한 453초 이후에는 더 이상 발생하지 않았다. FM1 모델과 FM2 모델의 최대 전단변위는 각각 78.8 μm, 47.4 μm로, FM1 모델에서 더 큰 전단변위가 확인되었다.
전단파괴의 발생 이전에는 수직변위가 탄성변형에 의존하므로 두 모델에서 동일한 수직변위를 보이는 것이 합리적인 결과이다. 그러나 전단파괴 이후에 각각 일정량의 수직변위(creation aperture)와 팽창각에 의한 수직변위가 추가되는 상이한 모델임에도 불구하고 유사한 수직변위를 보였다. 이는 전단파괴에 의한 수직변형량이 탄성변형량에 비해 상대적으로 작게 발생하기 때문이다. 예를 들면, 최대 주입압이 6.302 MPa일 때 단층에는 5.802 MPa의 압력 변화가 발생하게 되고(초기 압력 0.5 MPa), 유효수직응력의 변화가 이와 동일하다고 가정할 때 수직강성이 20 GPa/m인 단층에는 290 μm의 수직탄성변형이 유발된다(해석 결과, 유효수직응력의 변화량은 FM1의 경우 5.33 MPa, FM2의 경우 5.26 MPa로 나타났다). Fig. 11의 수직변위를 살펴보면, 대부분 탄성변형에 의한 값임을 확인할 수 있다. 전단파괴로 인해 FM1 모델에서 28 μm가, FM2 모델에서 경우 8.3μm의 수직변위가 발생하나, FM2 모델의 탄성변형이 FM1 모델보다 3.5 μm 크게 발생하여 두 모델간의 차이점이 뚜렷이 발현되지 않았다.
모니터링 지점 P2과 P3 지점에서의 변위를 살펴보면, 전반적으로 FM1 모델이 FM2 모델보다 더 큰 변위를 예측하는 것으로 나타났다. FM1 모델에서는 P2 지점과 P3 지점에서 모두 전단파괴가 발생하였고, 두 모니터링 지점에서 수직변위는 유사하였지만 전단변위는 뚜렷한 차이를 보였다. P2 지점에서는 420초 이후 서서히 전단변위가 발생하면서 경사방향으로 약 2.5 μm, 주향방향으로 약 0.2 μm의 최대 전단변위를 보였다(주향방향 전단변위는 해석모델의 외곽에서 주입지점을 향하는 방향이 양의 부호를 갖는다). 한편, P3 지점에서는 420초 이후 급격한 전단변위가 발생하여 약 20 μm의 전단변위를 보였다. 이러한 차이는 주입수의 흐름이 중력의 영향을 받기 때문으로, 주입공 상부 1.5 m 거리에서 발생한 최대전단변위는 2.0 μm 수준에 그쳤다. FM2 모델에서는 P2와 P3 지점에서 모두 전단파괴에 도달하지 않았으며, 전단변위는 모두 주입지점 주변의 미끄러짐에 동반된 전단방향 탄성변형에 의한 것으로 사료된다.
Fig. 14는 주입 후 453초일 때 예측된 전단변위와 전단파괴 발생 영역을 보여준다. 주입공 주변에서 최대 전단변위가 발생하였고, FM1에서 더 넓은 영역에 걸쳐 더 큰 전단변위가 관찰되었다.
3.2 수리학적 거동
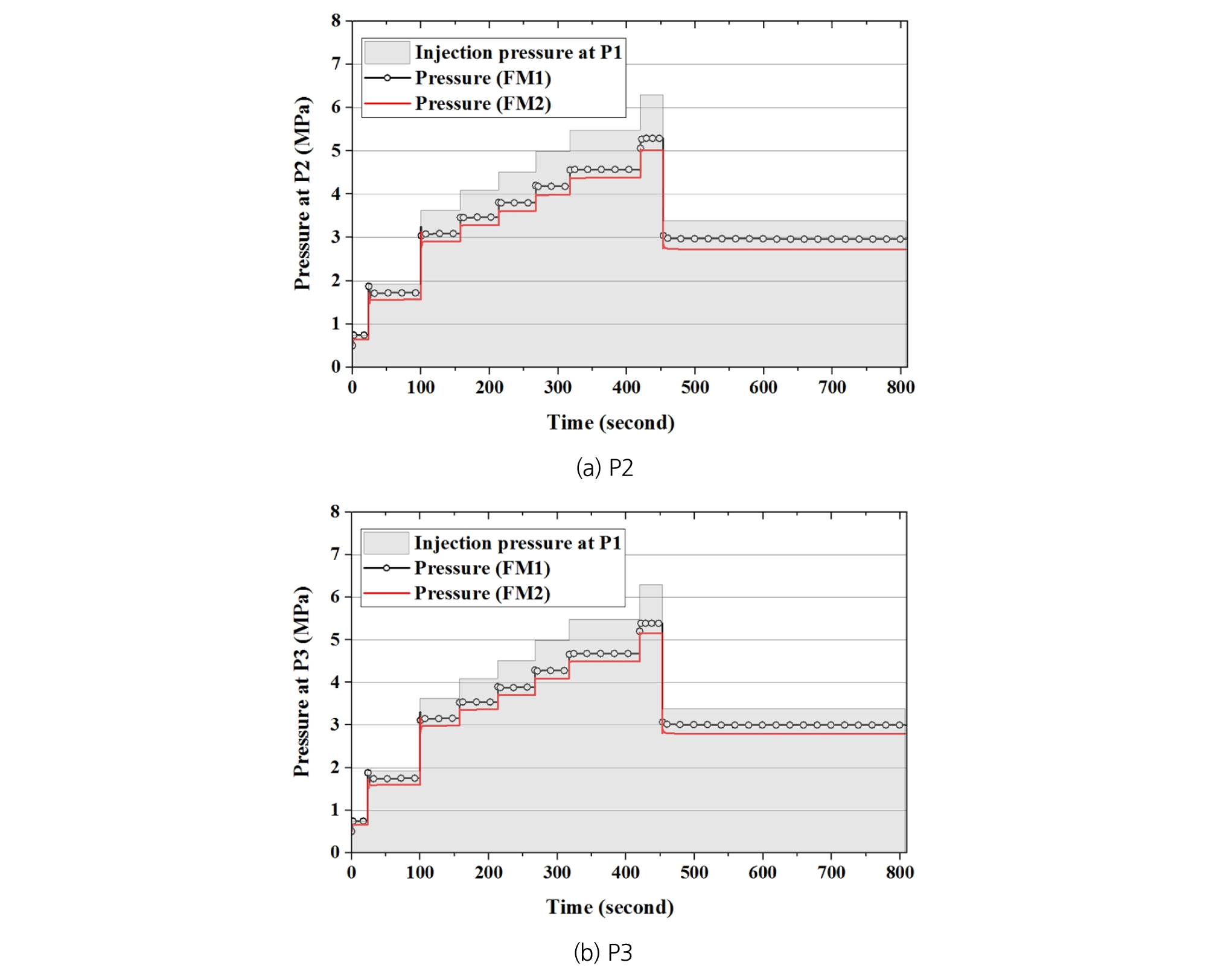
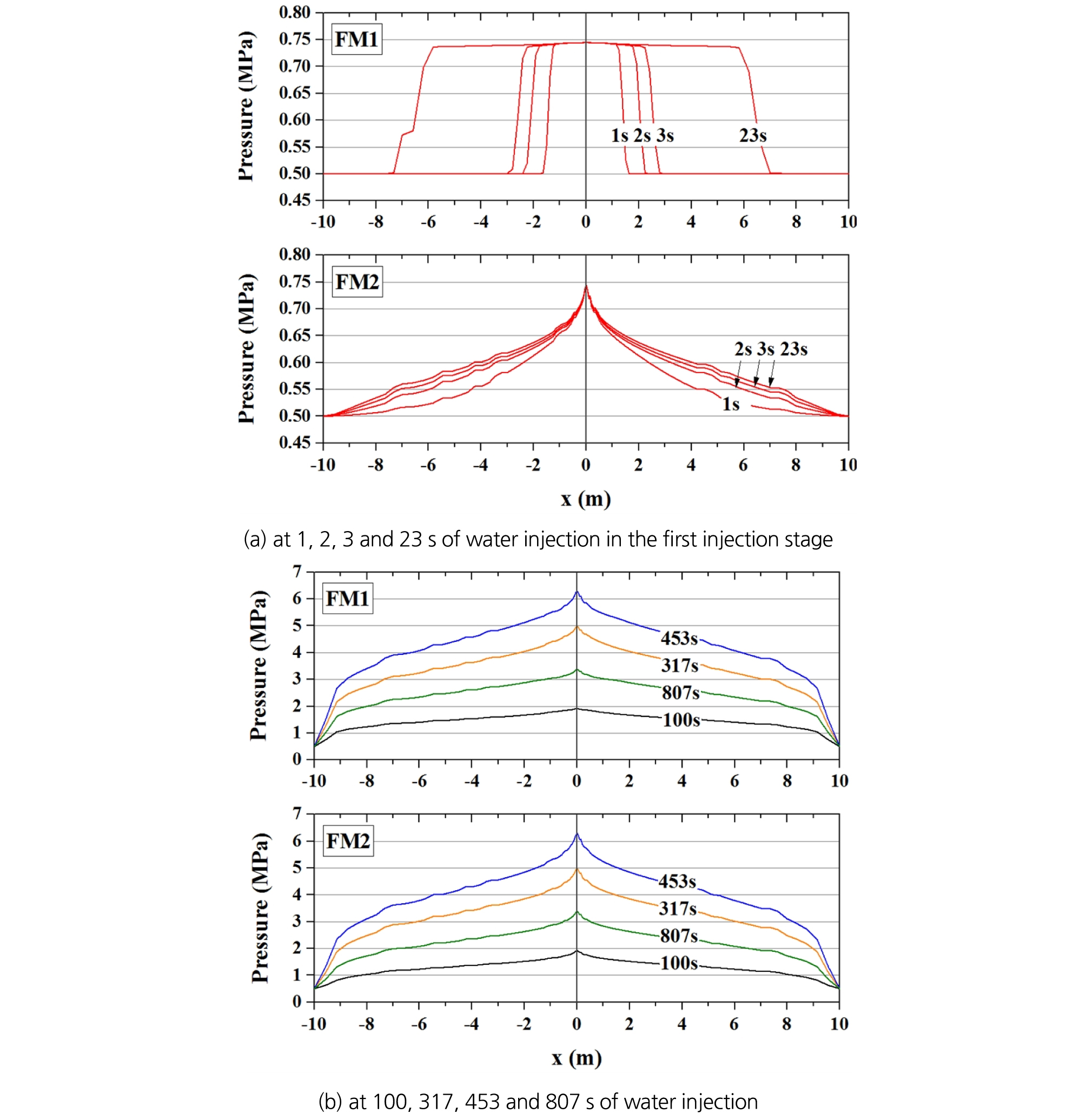
Fig. 15는 모니터링 지점 P2와 P3에서 예측된 압력을 도시한 것이다. 두 수리간극모델에서 모두 P2 지점에 비해 P3 지점의 압력이 높았으며, 이는 상기한 바와 같이, 중력의 영향으로 인해 주입수의 흐름이 완전한 동심원 형태를 이루는 것이 아니라 단층의 경사방향으로 더 유리하게 발달하였기 때문이다. 모니터링 지점에서의 압력은 주입압에 비해 낮은 수치였으나, 주입 후 수 초 이내에 압력이 전달되었고, 전반적으로 FM1 수리간극모델보다 FM2 수리간극모델에서 더 높은 압력 수준을 보였다.
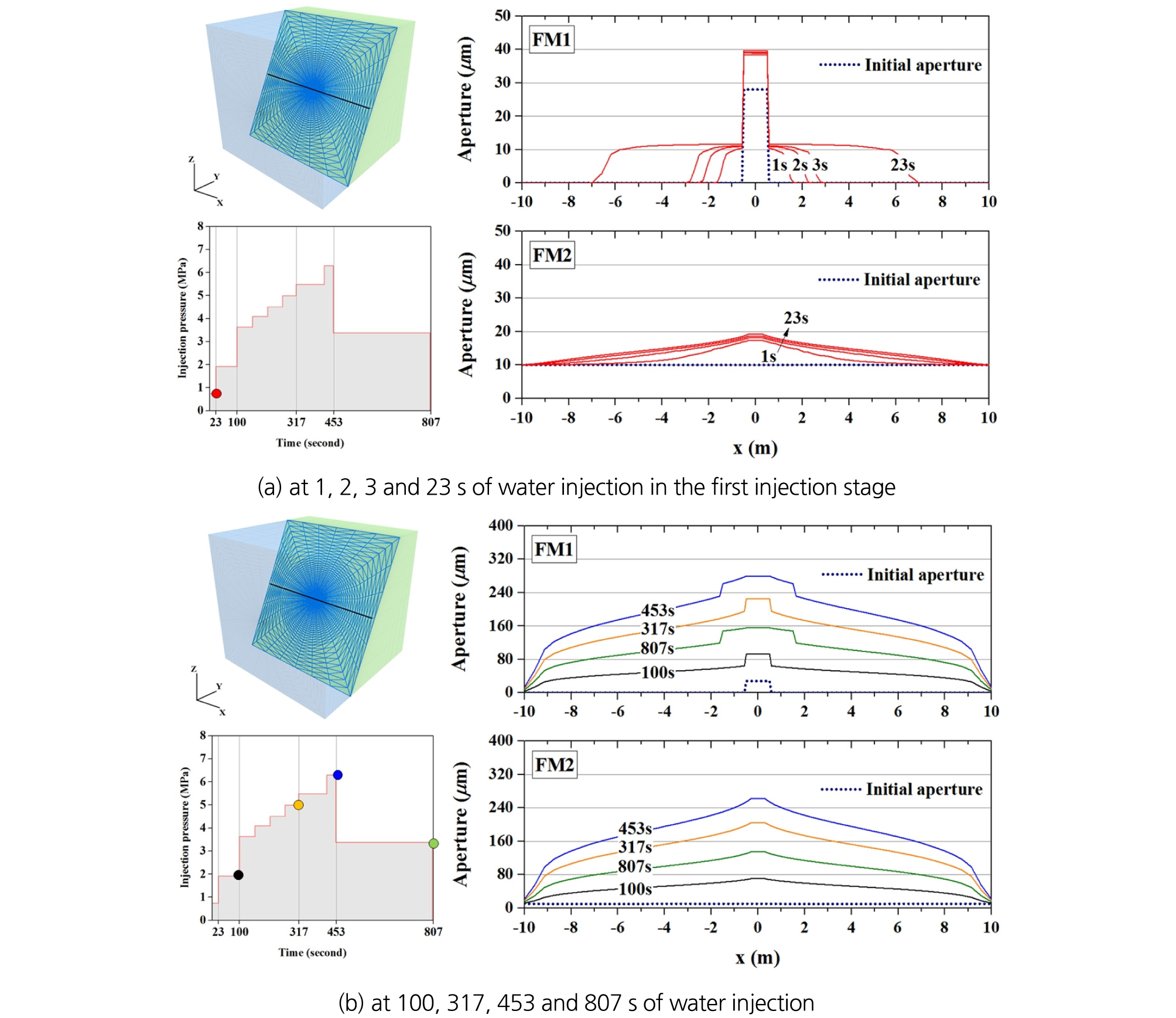
두 수리간극모델 간 압력 분포의 차이는 수리간극의 변화 양상을 살펴봄으로써 그 원인을 설명할 수 있다. Fig. 16과 Fig. 17은 각각 수리간극과 압력 변화를 보여주는 그림으로, 주입지점을 통과하는 주향방향 프로파일 상에서의 해석 결과이다. (a)는 첫 번째 주입단계(주입 후 1, 2, 3, 23초, 주입압 0.7446 MPa)의 해석 결과이며, (b)는 주입 후 100초(주입압 1.919 MPa), 317초(주입압 4.990 MPa), 453초(주입압 6.302 MPa), 807초(주입압 3.328 MPa) 경과 시의 해석 결과이다. 한편, Fig. 18은 주입 후 1, 3, 23초일 때 단층의 압력분포를 보여준다.
첫 번째 주입단계(~23초)에서 수리간극의 변화를 살펴보면(Fig. 16a), 두 모델에서 모두 주입 초반에 수리간극의 크기가 급격히 증가하는 것을 확인할 수 있다. 주입공 주변 직경 1.0 m의 파쇄 영역만을 초기 투수층(수리간극 28 μm)으로 간주하는 FM1 모델의 경우, 간극의 크기와 부피가 작아 파쇄 영역 내로 주입압이 즉각적으로 전달되었고(Fig. 17a의 FM1, Fig. 18의 FM1), 이에 따라 수직방향 유효응력 감소와 탄성변형에 의한 간극 변화가 발생하였다(Fig. 16a의 FM1). 초기 파쇄영역을 중심으로 불투수층이 순차적으로 투수층으로 전환되었고, 주입 후 23초에는 주입공으로부터 7.0 m 거리까지 투수층이 확장되었다. 불투수층과 투수층을 경계로 불연속적인 압력분포를 보이며, 투수층 내에서는 대부분 주입압에 상응하는 압력이 발달되는 것으로 나타났다. 반면, 단층면 전체를 투수층(수리간극 10 μm)으로 가정하는 FM2의 경우, 주입 후 1초 이내에 전체 단층에 완만한 압력 구배가 발달한 것으로 나타났고, 주입 후 23초 이후에는 모델의 경계부까지 압력이 전달되는 경향을 보였다(Fig. 17a의 FM2, Fig. 18의 FM2). 수리간극 역시 압력(유효 수직응력) 변화에 상응하는 탄성변형으로 인해 증가하는 것으로 나타났으며 연속적인 크기 분포를 보였다(Fig. 16a의 FM2).
FM1 모델에서 100초 이후의 결과들을 살펴보면, 해석모델의 경계까지 수리간극이 증가하여 투수층으로 전환되고, 첫 번째 단계(~23초)의 결과와는 달리 완만한 압력 구배가 형성된 것을 확인할 수 있다(Fig. 16b의 FM1, Fig. 17b의 FM1). 주입 후 100초, 317초 경과 시의 수리간극 변화는 탄성변형에 의해 것이며, 453초 경과 시에는 초기 파쇄영역 주변에서 전단파괴로 인한 creation aperture가 추가된 결과이다. 807초 경과 시에는 주입압의 감소로 인해 탄성적인 수리간극이 감소하지만, 전단파괴에 의한 creation aperture는 유지된다. 따라서 파쇄영역을 경계로 하는 불연속적인 수리간극 분포를 보이게 되며, 전단파괴로 인하여 주입공으로부터 좌우로 약 1.6 m 거리까지 전단파괴가 발생하였음을 확인할 수 있다. 한편, FM2 모델에서는 첫 번째 주입단계의 결과와 유사하게 연속적인 압력분포 및 수리간극 분포를 보였다(Fig. 16b의 FM2, Fig. 17b의 FM2). 전반적으로, 동일한 지점에서 FM2 모델의 압력과 수리간극이 FM1 모델에 비해 작게 해석되었으며, 이는 전단파괴 이후 발생한 수리간극의 변화보다는 초기 수리간극 조건의 차이에 의한 것으로 보인다. 앞서 Fig. 18에서 보인 주입 초기의 압력 분포에서 확인할 수 있듯이, FM1 모델에서는 주입 지점 주변부터 압력이 집중되다가 투수층이 확장됨에 따라 경계부까지 순차적인 방식으로 압력 전달이 이루어지는 반면, FM2 모델에서는 단층면 전체가 투수층이므로 주입 초기부터 넓은 영역에 걸쳐 압력이 완만한 구배를 이루며 분포하는 경향을 보였다. 이에 따라 FM1 모델에서 더 넓은 영역의 전단파괴가 관찰되었고, 전단변위도 크게 해석된 것으로 판단할 수 있다.
한편, Fig. 17의 결과를 살펴보면 경계부에서 압력이 급격히 감소하는 특징을 보였다. 일반적인 방사형 유동의 경우 거리에 따라 압력이 지수적으로 감소하는 특징을 갖는다. 본 연구의 벤치마크 모델이 수리간극을 변화를 반영하는 특수한 경우이기는 하나, 이를 고려하더라도 경계부에서 압력이 부자연스럽게 0.5 MPa로 감소하는 것을 확인할 수 있다. 이는 벤치마크 모델의 크기가 지나치게 작게 설정되어 주입지점으로부터 10 m 거리에서 0.5 MPa의 압력이 일정하게 유지되는 경계조건이 비합리적임을 의미하는 것이다.
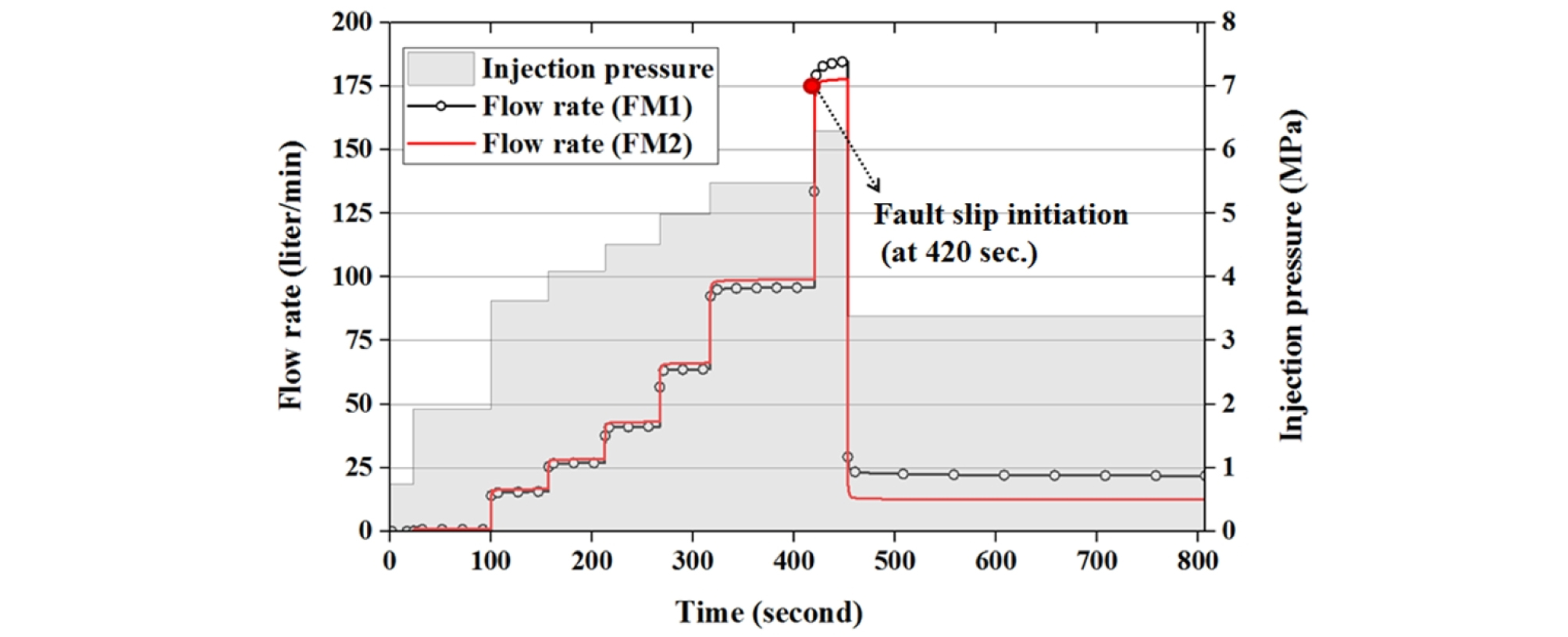
Fig. 19는 시간에 따른 물 주입율을 해석한 결과이다. 전단파괴 이전에는 주입압의 증가에 따라 물 주입율이 선형적으로 증가하는 경향을 보였으며, 두 모델에서 유사한 결과를 나타내었다. 각 주입단계의 초반에 주입율이 급격한 증가를 보이다가 일정한 값을 유지하는 것으로 나타났는데, 이는 본 연구의 해석모델에서 수리간극의 부피가 지속적으로 증가하고 있음을 의미한다. 만약 일정 주입압 조건에서 수리간극의 부피가 증가하지 않는다면, 일정 시간 경과 후 주입압은 유지되지만 주입율은 점점 감소하여 일정한 값으로 수렴할 것이다. 두 수리간극 모델에서 모두 전단파괴가 개시된 420초를 전후로 주입율이 급격하게 증가하는 것으로 나타났고, FM2 모델보다 FM1 모델에서 더 큰 주입율 변화를 보였다.
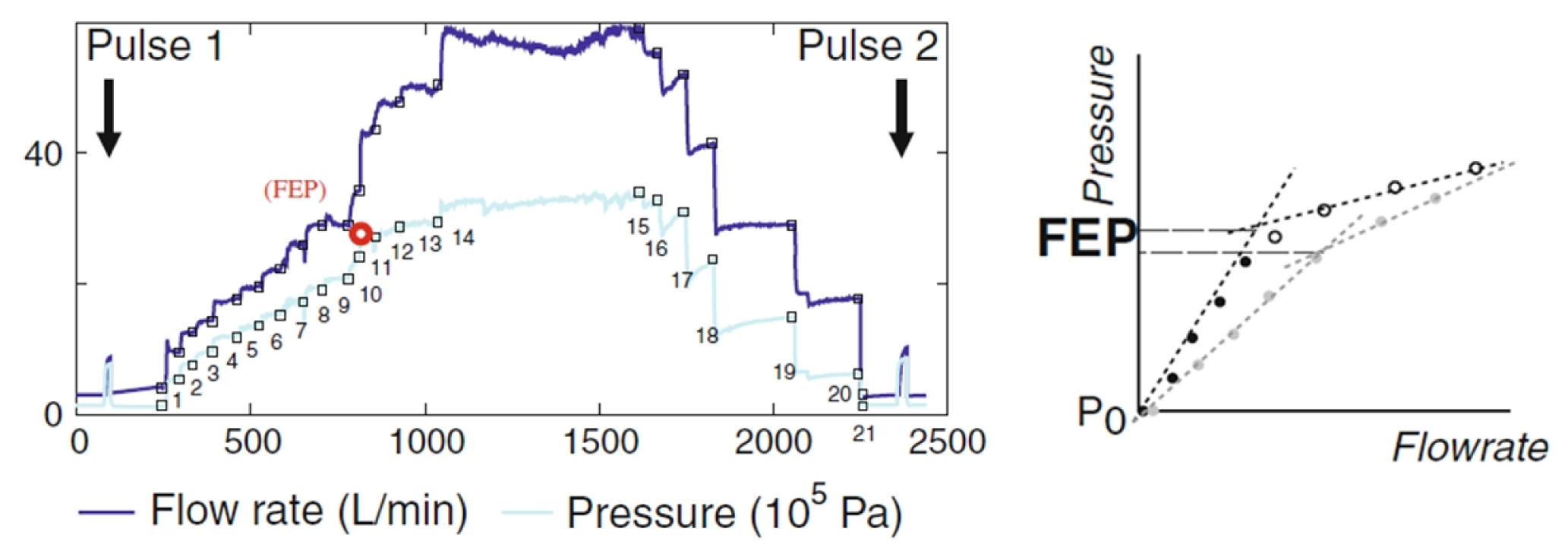
급격한 주입율의 증가는 단층의 전단파괴로 인해 전단변위와 수직변위가 동시에 발생하였기 때문으로 해석할 수 있다. Guglielmi 외(2014)는 단층(균열) 주입시험(SIMFIP)의 주입압과 주입율 곡선을 통해 단층의 균열확장압력(fracture extension pressure, FEP)을 추정할 수 있다고 하였다. 균열확장압력 이하의 압력에서 균열이 수리역학적으로 탄성적 거동을 보이며, 그 이상에서는 균열이 손상을 입고 확장되는 비탄성적 거동을 보인다. Fig. 20은 단층 주입시험(SIMFIP)의 전형적인 시험결과를 보여주는 것으로 주입율에 대한 주입압 곡선의 변곡점, 즉 주입압의 증분에 비해 주입율의 증분이 현저히 크게 발생하는 시점에서 균열개시압력을 결정할 수 있다. 본 연구의 해석 결과(Fig. 19)를 Fig. 20의 현장시험 결과와 비교하여 볼 때, 개발된 수치모델이 현장 조건 주입시험을 적절히 모사할 수 있음을 확인할 수 있다.
3.3 Task B 연구현황
Task B에는 한국지질자원연구원을 비롯하여 독일(Federal Institute for Geosciences and Natural Resources/Centre for Environmental Research), 캐나다(Canadian Nuclear Safety Commission), 스위스(Swiss Federal Nuclear Safety Inspectorate), 대만(Institute of Nuclear Energy Research), 미국(Lawrence Berkeley National Laboratory)의 6개 연구팀이 참여하고 있으며, 2018년 4월부터 독일 German Research Centre for Geosciences(GFZ)가 추가 참여의사를 밝혀 현재 7개의 연구팀이 모델링 기법을 개발하고 있다.
2017년 캐나다에서 개최된 제4차 워크숍에서 각 연구팀이 1단계 연구 결과를 발표하였으나, 당시 미제출 자료가 많아 해석모델의 적절한 비교분석이 이루어지지 못하였고, 제출한 연구팀들의 해석 결과도 큰 차이를 보였다. 해석결과의 차이(또는 오류)는 각 수치해석 모델 내에서 수리 간극을 정의하고 수치화하는 과정의 기술적, 이론적 차이에 기인할 것이며, 이에 대한 근본적인 해결을 위하여 추가해석의 필요성이 제기되었다. 따라서 Task B의 연구팀들은 FM2 수리간극모델에 대해서 7가지 시나리오에 대한 추가 해석을 수행하여 각 해석코드/기법의 완성도를 높이고 타당성을 검증하기로 합의하였다. 2018년 8월 현재, 참여기관별로 1단계 연구의 추가해석(BMT1~BMT7)과 2단계 연구가 진행 중에 있으며, 지난 4월 제5차 워크숍에 이어 10월 한국에서 개최되는 제6차 워크숍에서 각국의 해석결과를 비교, 논의할 예정이다. 추가된 7가지 시나리오(Benchmark Model Test(BMT) 1~7)는 다음과 같다.
1) BMT1: Uncoupled fluid flow during constant pressure injection
2) BMT2: One-way coupled fluid flow during constant pressure injection
3) BMT3: Two-way coupled fluid flow during constant pressure injection
4) BMT4: Uncoupled fluid flow during step pressure injection
5) BMT5: One-way coupled fluid flow during step pressure injection
6) BMT6: Two-way coupled fluid flow during step pressure injection
7) BMT7: One-way coupled fluid flow during step pressure with activation
BMT1, BMT2, BMT3는 각 팀의 해석모델이 단층의 수리-역학적 커플링을 적절히 재현하는지를 검토하기 위한 해석 케이스로, 모두 일정 압력(1 MPa)이 800초간 유지되는 조건이다. BMT1의 경우, 단층에 매우 큰 수직강성을 적용하여 물 주입으로 인해 간극과 투수계수가 변화하지 않는 조건을 가정한다. BMT2와 BMT3의 경우, 낮은 수직강성을 적용하여 물 주입으로 인해 간극이 변화하게 되며, BMT2에서는 일정한 투수계수를 가정하지만 BMT3에서는 투수계수의 변화를 해석에 반영한다. 따라서 BMT1과 BMT2의 결과, BMT2와 BMT3의 결과를 비교함으로써 단층의 저류계수(storativity)와 투수량계수(transmissivity)의 변화가 해석결과에 미치는 영향을 검토할 수 있다. BMT4, BMT5, BMT6는 각각 BMT1, BMT2, BMT3와 동일한 조건이지만, Fig. 3의 단계적 주입압이 적용된다. BMT1~BMT6에서는 높은 전단강도를 가정하여 단층 미끄러짐을 허용하지 않으며, BMT7의 경우 BMT5와 동일한 조건에서 단층의 미끄러짐으로 인한 영향을 함께 검토하게 된다.
4. 요약 및 결론
본 논문에서는 국제공동연구인 DECOVALEX-2019 프로젝트의 Task B의 1단계 연구내용과 현황을 소개하였다. Task B의 주제는 ‘Fault slip modeling’으로 단층 내주입수로 인해 발생하는 전단파괴 및 수리역학적인 거동을 예측하기 위한 해석코드를 개발하는 데에 그 목적이 있다. 본 연구에서는 TOUGH-FLAC 연동해석 기법을 사용하여 단계적 압력의 물 주입에 따른 단층의 미끄러짐과 이에 따른 수리-역학적 연계거동을 모델링하였다. 두 가지 수리간극모델의 수리-역학적 관계를 수치화하기 위하여 TOUGH2의 연속체 요소와 FLAC3D의 불연속 인터페이스 요소를 연동할 수 있는 모델링기법을 수립하였으며, 역학적 변형으로 야기되는 수리특성 변화와 함께 해석 메쉬의 기하학적 변화를 수리해석에서 고려할 수 있도록 하는 커플링 모듈을 개발하였다. 각 수리간극모델의 해석 결과를 바탕으로 단층 및 주변 암반의 변위와 응력을 통해 전단거동 및 파괴 메커니즘 등을 고찰하였고, 수리간극의 변화 양상과 원인, 수리간극과 압력 분포의 관계 등을 자세히 살펴보았다. 제3장에서 논의한 바와 같이, 참여 연구팀들의 해석 결과가 큰 차이를 보였으며, 본 연구에서 제시한 해석기법 역시 지속적인 개선과 검증이 필요한 상태이다. 그러나 이론적인 분석 및 전형적인 현장 자료와의 비교 등을 통해 본 연구의 해석모델이 논리적으로 큰 모순이 없음을 확인하였고, 주입에 의한 단층 재활성화와 제반 거동을 합리적 수준에서 재현할 수 있을 것으로 기대할 수 있었다. 다만, 타 연구팀들에 비해 본 연구의 모델에서 압력의 전달 속도가 빠르게 나타나는 경향이 있고, 이에 따라 주입공 주변의 압력 및 변위가 상대적으로 크게 해석되었다. 향후 새롭게 제안된 추가 해석을 통하여 이에 대한 원인 분석 및 개선이 이루어져야 할 것으로 생각된다. 본 연구에서 개발한 해석기법은 Task B에 참여하는 국외 연구팀들과의 의견 교류와 워크숍을 통해 지속적으로 개선하는 한편, 향후 연구를 통해 현장시험에 적용하여 타당성을 검증할 예정이다.