1. 서 론
2. 일반화된 H-B (GHB) 파괴조건식
2.1 최대주응력-최소주응력 관계식
2.2 무차원 변환된 GHB 파괴조건식
2.3 무차원 GHB 파괴조건식의 기하학적 특징
3. GHB 파괴조건식의 근사 Mohr 파괴포락선 유도
3.1 수직응력-접선마찰각 관계식의 특성 분석
3.2 수직응력-접선마찰각 관계식의 1차 및 2차 최적 다항식
3.3 근사 GHB Mohr 파괴포락선
4. 근사 Mohr 파괴포락선식의 정확성 검증
5. 요약 및 결론
1. 서 론
암반(rock mass)이나 무결암(intact rock)의 파괴조건식은 선형과 비선형 파괴조건식으로 구분할 수 있다. 선형 파괴조건식에서는 파괴 시 팔면체전단응력(octahedral shear stress, Obert & Duvall, 1967)의 크기가 팔면체수직응력(octahedral normal stress)의 크기와 선형 비례관계를 보이며 비선형 파괴조건식에서는 이 관계가 비선형적이다. 잘 알려진 선형 파괴조건식으로 Mohr- Coulomb(M-C) 식, Drucker-Prager 식(Alejano & Bobet, 2012), 수정 Weibols-Cook 식(Zhou, 1994), 수정 Lade 식(Ewy, 1999), Mogi-Coulomb 식(Al-Ajmi & Zimmerman, 2005) 등이 있다. 반면에 Hoek-Brown(H-B) 식(Hoek, 1983, Hoek et al., 2002), HBMN 식(Benz et al., 2008), HB-JP 식(Lee, 2012), HB-WW 식(Lee et al., 2012) 등은 비선형 파괴조건식의 대표적 사례이다. 각 파괴조건식은 사용의 간편성과 강도예측의 정확성 측면에서 장단점을 동시에 가지고 있으므로 사용목적에 적합한 파괴조건식을 선택하는 것이 중요하다. ISRM 표준시험법(Ulusay, 2014)에서는 암반공학 분야에서 많이 적용되는 주요 파괴조건식들의 특징과 적용한계를 기술하고 있다.
특히 H-B 식은 무결암과 절리암반에 모두 적용 가능한 비선형 파괴조건식이며 최근 암반의 표준 파괴함수의 하나로 간주되고 있다. 파괴 시 최대주응력(σ1)과 최소주응력(σ3)의 관계를 정의하는 H-B 식은 1980년 처음 제안된 이래로 꾸준한 개정과정을 거쳐 가장 최신의 형태인 일반화된 H-B(Generalized H-B, GHB) 식으로 발전하였다(Hoek et al., 2002). GHB 식에서는 GSI (Geological Strength Index, Hoek, 1999) 지수를 이용하여 현장 암반의 절리분포 및 절리면 특성에 따라 무결암의 강도를 현장 암반의 강도로 저감시키는 체계적인 절차를 제공한다. 여기서 GSI 지수는 0과 100 사이의 정수로서 100에 가까운 값일수록 양호한 암반을 의미한다. 최근 H-B 식은 유한요소법에 기초한 탄소성해석의 항복함수(Clausen & Damkilde, 2008)로 사용되거나 상계정리 한계해석법(upper bound limit analysis, Chen, 2008)을 기반으로 하는 터널붕락해석(Yang & Huang, 2011), 사면안전율 계산 (Mao et al., 2012), 암반기초 지지력 산정(Merifield et al. 2006)의 근사 활동조건식(slip condition)으로 사용되는 등 수치해석 분야에서도 그 적용범위를 넓혀가고 있는 추세이다.
그러나 GSI=100인 경우를 제외하면 GHB 파괴조건식을 명시적 전단강도식 즉, Mohr 파괴포락선으로 표시하기 것이 어렵다는 점이 GHB 파괴함수의 최대 약점으로 지적되고 있다. GSI=100인 경우 GHB 식에 대응되는 명시적 Mohr 파괴포락선식은 Bray의 해(Hoek, 1983)가 최초로 발표된 이 후 Ucar(1986), Londe(1988), Lee(2014)에 의해서도 유도되었다. GSI≠100인 경우 Mohr 파괴포락선식의 해석적 정해는 아직까지 유도되지 못하고 있는 실정이지만, 최근 Lee & Pietruszczak (2017)은 정해에 매우 근사하는 해석적 Mohr 파괴포락선 관계식을 얻는 방법을 발표하였다. Lee & Pietruszczak(2017)의 연구에서는 GHB 식에 내포된 접선마찰각(∅i)과 수직응력(σ)의 관계식으로부터 ∅i를 σ의 명시적 함수로 표시하기 위해 Taylor 다항식 근사법이 이용되었다. 또한 Lee & Pietruszczak (2018b)의 연구에서는 다항식 최적화 기법을 적용하여 최소주응력(σ3)을 σ의 근사식으로 표현하는 방법에 의해 GHB 식의 해석적 Mohr 파괴포락선 식을 유도하였다.
암반공학 및 지반공학 구조물의 안정성 평가에 널리 활용되는 한계평형해석법(limit equilibrium analysis, Wyllie & Mah, 2004)과 한계해석법 등을 포함한 여러 수치해석 기법들이 명시적 Mohr 파괴포락선식의 존재를 전제로 하고 있음을 고려할 때 GHB 식의 해석적 Mohr 파괴포락선식이 제시될 경우 GHB 파괴함수의 적용범위를 대폭 넓힐 수 있을 것으로 기대된다. 또한 GHB 식의 Mohr 파괴포락선식은 사면이나 터널 주변에서 암반블록이 활동할 가능성을 판단하는 절리면 비선형 전단강도식으로 활용될 수도 있다.
이 연구에서는 Lee & Pietruszczak(2017, 2018b)의 연구에서 제안된 GHB 파괴조건식의 근사 Mohr 포락선 유도과정을 바탕으로 이전의 경우와 다른 접근법을 통해 근사 Mohr 포락선식을 유도하는 과정이 제안되었고, 유도된 근사 Mohr 파괴포락선의 정밀성에 대한 정략적인 평가가 이루어졌다. 또한 무차원 수직응력–접선마찰각 관계식의 1차 다항식 및 2차 다항식 최적근사를 기반으로 유도된 근사 Mohr 파괴포락선을 수치해석적으로 구한 Mohr 파괴포락선 정해와 비교함으로써 1차 다항식 최적근사법에 대한 2차 다항식 최적근사 방법의 상대적 우수성을 정량적으로 검증하였다. 제안된 근사 Mohr 포락선의 유도와 관련된 아이디어는 Lee & Pietruszczak(2018a)에 의해 처음 제시되었으나, 이 연구를 통해 구체적인 해석적 수식화 및 검증이 이루어졌다. 한편, Taylor 다항함수 근사법보다 발전된 형태인 다항식 최적화 근사법을 적용하였으며 Balmer의 파괴포락선 관계식(Balmer, 1952)에 근거하지 않았다는 측면에서 이 연구는 Lee & Pietruszczak(2018b) 및 Lee & Pietruszczak(2017)의 연구와 차별성을 보인다.
2. 일반화된 H-B (GHB) 파괴조건식
2.1 최대주응력-최소주응력 관계식
GHB 파괴조건식에서는 암반의 파괴에 필요한 최대주응력(σ1)의 크기를 최소주응력(σ3)의 함수로 다음과 같이 예측한다 (Hoek et al., 2002).
| $$\sigma_1=\sigma_3+\sigma_{ci}\left(m_b\frac{\sigma_3}{\sigma_{ci}}+s\right)^a$$ | (1) |
여기서 σci는 무결암의 일축압축강도이고 강도정수 mb, s, a는 GSI 지수를 이용하여 다음과 같이 정의된다.
| $$m_b=m_i\;\exp\left(\frac{GSI-100}{28-24D}\right)$$ | (2) |
| $$s=\exp\left(\frac{GSI-100}{9-3D}\right)$$ | (3) |
| $$a=0.5+\frac16(e^{-GSI/15}-e^{-20/3})$$ | (4) |
식 (2)에서 mi는 무결암의 암종과 조직(texture)에 따라 경험적으로 결정된 강도정수이다. 식 (2)과 식 (3)의 D는 응력이완이나 굴착에 기인한 암반의 교란정도를 지시하는 지수로서 0과 1 사이의 값을 갖는다. 교란되지 않은 양호한 암반일수록 D값은 0에 가까운 값을 갖는다. 식 (4)을 살펴볼 때 GSI=100이면 a=0.5이므로 이 경우 GHB 파괴조건식은 최초 제안된 H-B식(Hoek, 1983)과 동일함을 알 수 있다.
2.2 무차원 변환된 GHB 파괴조건식
Rojat et al. (2015)이 제안한 수직응력 변환관계식
| $$P=\frac\sigma{m_b^{a/(1-a)}\sigma_{ci}}+\frac s{m_b^{1/(1-a)}}$$ | (5) |
을 적용하면 GHB 파괴조건식 (1)은 P1-P3 평면에서 원점을 지나는 다음 식으로 표시된다.
| $$P_1=P_3+P_{{}_3}^a$$ | (6) |
여기서 P1과 P3은 각각 최대 및 최소 주응력이 식 (5)에 의해 변환된 결과이다. 그러므로 GHB 파괴함수의 곡선형태는 강도정수 a에 의해 결정된다는 사실을 식 (6)으로부터 알 수 있다.
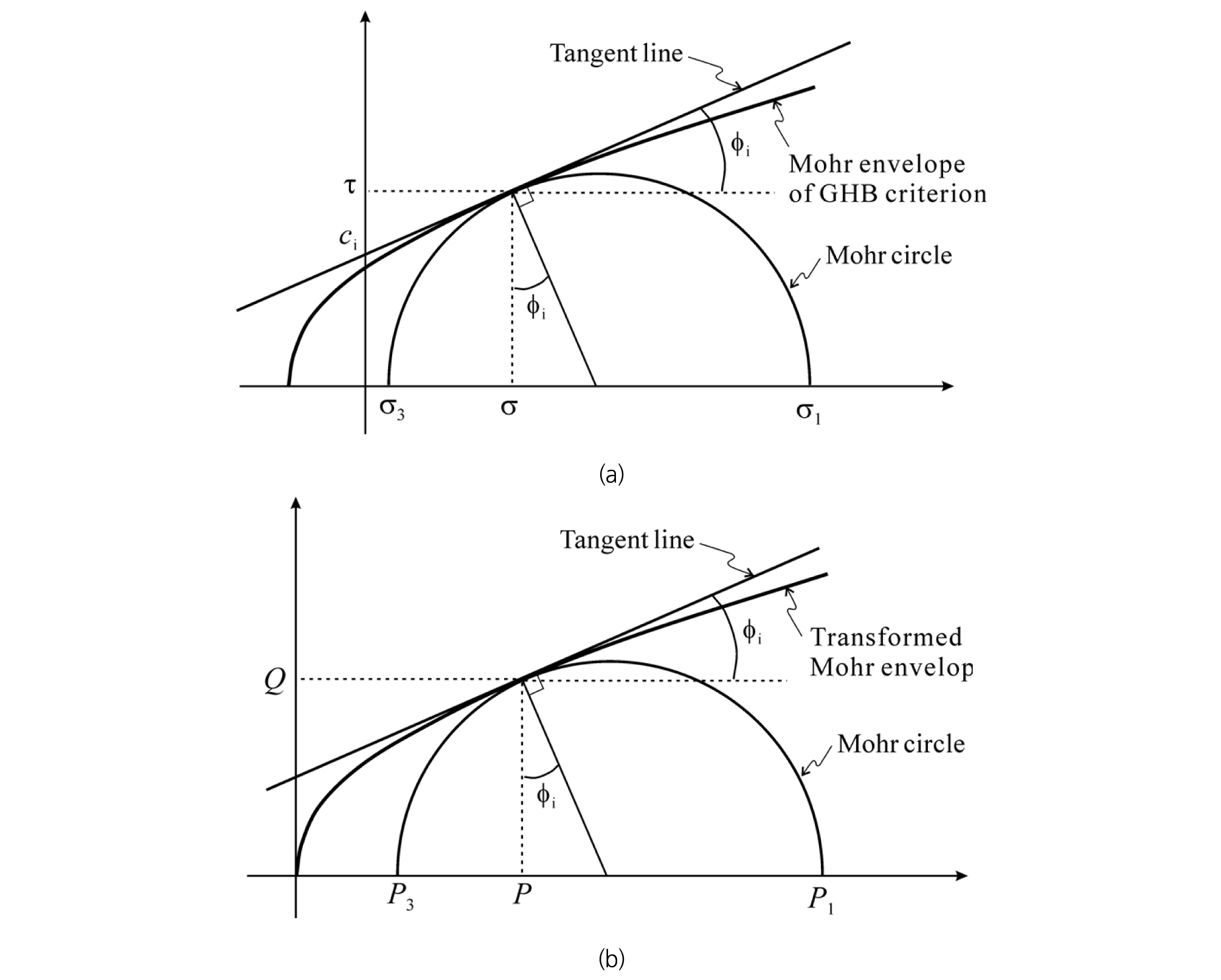
또한 Lee & Pietruszczak (2017)이 제안한 전단응력에 대한 변환 관계식, 식 (7)을 고려하면 σ-τ 평면에 도시된 Mohr 파괴포락선은 P-Q 평면에서 원점을 지나는 무차원 파괴포락선으로 변환된다 (Fig. 1). 그림에서 ∅i와 ci는 각각 접선마찰각과 접선점착력을 의미한다.
| $$Q=\frac\tau{m_b^{a/(1-a)}\sigma_{ci}}$$ | (7) |
2.3 무차원 GHB 파괴조건식의 기하학적 특징
Fig. 1(b)에 도시한 무차원 Mohr 원과 Mohr 파괴포락선의 기하학적 관계로부터 ∅i, P, Q 사이에는 다음의 관계식이 성립함을 보일 수 있다 (Lee & Pietruszczak, 2017).
| $$P=\left(\frac a2\right)^{1/(1-a)}\left(\frac{1-\sin\varnothing_i}{\sin\varnothing_i}\right)^{1/(1-a)}\left(1+\frac{\sin\varnothing_i}a\right)$$ | (8) |
| $$Q=\left(\frac a2\right)^{a/(1-a)}\;\left(\frac{\cos\varnothing_i}2\right)\left(\frac{1-\sin\varnothing_i}{\sin\varnothing_i}\right)^{a/(1-a)}$$ | (9) |
그러므로 식 (8)에서 ∅i를 P의 명시적인 해석식으로 표시할 수 있다면 이를 식 (9)에 대입하여 Mohr 파괴포락선의 해석적 수식을 유도할 수 있다. 그러나 a=0.5인 경우가 아니면 즉, GSI=100인 경우가 아니면 식 (8)의 ∅i를 P의 해석적 수식으로 표시하는 것이 곤란한 것으로 알려지고 있다. 대안으로 이 연구에서는 식 (8)의 ∅i를 P의 근사적인 해석식으로 표현하는 방법을 제안하였다.
3. GHB 파괴조건식의 근사 Mohr 파괴포락선 유도
3.1 수직응력-접선마찰각 관계식의 특성 분석
P는 수직응력 σ의 무차원 변환을 나타내므로 GHB 파괴조건식에 내포되어 있는 수직응력과 접선마찰각의 상호관계는 식 (8)으로 설명할 수 있다. 그리고 x=sin ∅i라 하고 0°≤∅i≤90°임을 고려하면 식 (8)은 x∈[0, 1]의 식으로 다음 같이 다시 기술될 수 있다.
| $$\widetilde P=\left(\frac1x-1\right)\;H(x)$$ | (10) |
여기서
| $$\widetilde P=\left(\frac2a\right)\;P^{1-a}$$ | (11) |
| $$H(x)=\left(1+\frac xa\right)^{1-a}$$ | (12) |
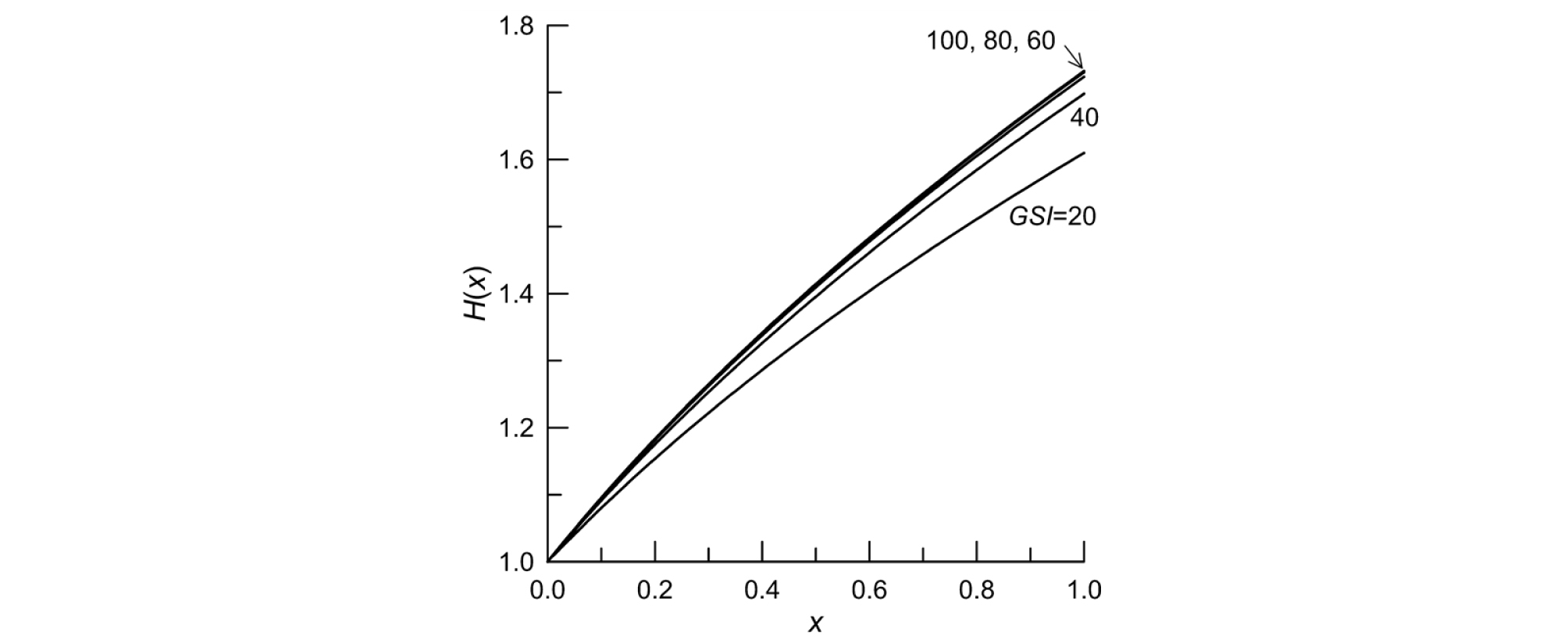
Fig. 2는 GSI 값이 함수 H(x)의 그래프 형태 변화에 미치는 영향을 보여준다. 함수 H(x)는 위로 볼록한 부드러운 곡선이며 GSI 값이 클수록 곡률(curvature)이 감소하여 직선에 가까워지는 특징을 보여준다. 또한 GSI≥60일 때 H(x)의 그래프 형태는 GSI 값에 거의 영향을 받지 않음을 알 수 있다.
이 연구에서는 식 (12)로 주어진 함수 H(x)를 구간 0≤x≤1에서 1차 또는 2차 다항식으로 최적 근사시킨 후 이 근사 다항식을 이용하여 GHB 파괴조건식의 Mohr 파괴포락선을 근사적으로 표현하는 방법이 시도되었다. H(x)를 1차 또는 2차 다항식으로 근사시킬 경우 식 (10)은 해석적 근(root)이 존재하는 x에 대한 2차 또는 3차 방정식이 된다.
3.2 수직응력-접선마찰각 관계식의 1차 및 2차 최적 다항식
최고차항의 차수가 n이고 연속인 다항함수(polynomial function)로 이루어진 선형 다항식 공간 Rn[0, 1]에 포함된 임의 두 함수의 내적(inner product)은 다음과 같이 정의할 수 있다.
| $$<f,\;g>=\int_0^1f\;g\;dx,\;\;\;\;\;\;f,\;\;g\in R_n\;\left[0,\;1\right]$$ | (13) |
또 선형 다항식 공간 Rn[0, 1]을 생성하는 정규직교(orthonormal) 기저함수를 ui(i=0, 1, …, n)라 하면 기저함수들은 다음의 조건을 만족해야한다.
| $$\left\|\;u_{i\;}\right\|=\sqrt{<u_i,\;u_i>}=1$$ | (14) |
| $$<u_i,\;u_i>=0\;\;\;\;\;\;\mathrm{for}\;\;\;\;i\neq j$$ | (15) |
그러므로 선형 다항식 공간 R1[0, 1]을 생성하는 두 정규직교 기저함수는
| $$u_0=1,\;\;\;\;\;\;\;u_1=\sqrt{12}\;\left(x-\frac12\right)$$ | (16) |
이고 선형 다항식 공간 R2[0, 1]를 생성하는 3개의 정규직교 기저함수는 식 (17)과 같다.
| $$u_0=1,\;\;\;\;\;\;\;u_1=\sqrt{12}\;\left(x-\frac12\right),\;\;\;\;\;\;\;\;\;\;u_2=\sqrt{180}\;\left(x^2-x+\frac16\right)$$ | (17) |
이제 구간 0≤x≤1에서 함수 H(x)의 1차 다항함수 최적 근사식 는 H(x)를 선형 다항식 공간 R1[0, 1]에 직교투영(orthogonal projection, Bretscher, 2005)하여 얻을 수 있으며, 이를 수식으로 표현하면 식 (18)과 같다.
| $$\begin{array}{l}\widehat{H_1}(x)=Pro{j_R}_1\;H(x)=\sum_{i=0}^1<u_i,\;H(x)>u_i\\\;\;\;\;\;\;\;\;\;\;=12\omega_2x+(\omega_1-6\omega_2)\end{array}$$ | (18) |
여기서
| $$\omega_1=\frac{(1+a)^{2-a}a^{a-1}-a}{2-a}$$ | (19) |
| $$\omega_2=\frac{a(3+a)-(1+a)^{2-a}a^{a-1}(3a-1)}{2(2-a)(3-a)}$$ | (20) |
유사한 과정에 의해 구간 0≤x≤1에서 함수 H(x)의 2차 다항식 최적 근사식 는 H(x)를 선형 다항식 공간 R2[0, 1]에 직교투영하여 다음 식과 같이 표시할 수 있다.
| $$\begin{array}{l}\widehat{H_2}(x)=Pro{j_R}_2\;H(x)=\sum_{i=0}^2<u_i,\;H(x)>u_i\\\;\;\;\;\;\;\;\;\;\;=180\omega_3x^2+(12\omega_2-180\omega_3)x+(\omega_1-6\omega_2+30\omega_3)\end{array}$$ | (21) |
여기서
| $$\omega_3=\frac{(19a-1)a^a(1+a)^{2-a}-a(7a^2+17a+12)}{6(2-a)(3-a)(4-a)}$$ | (22) |
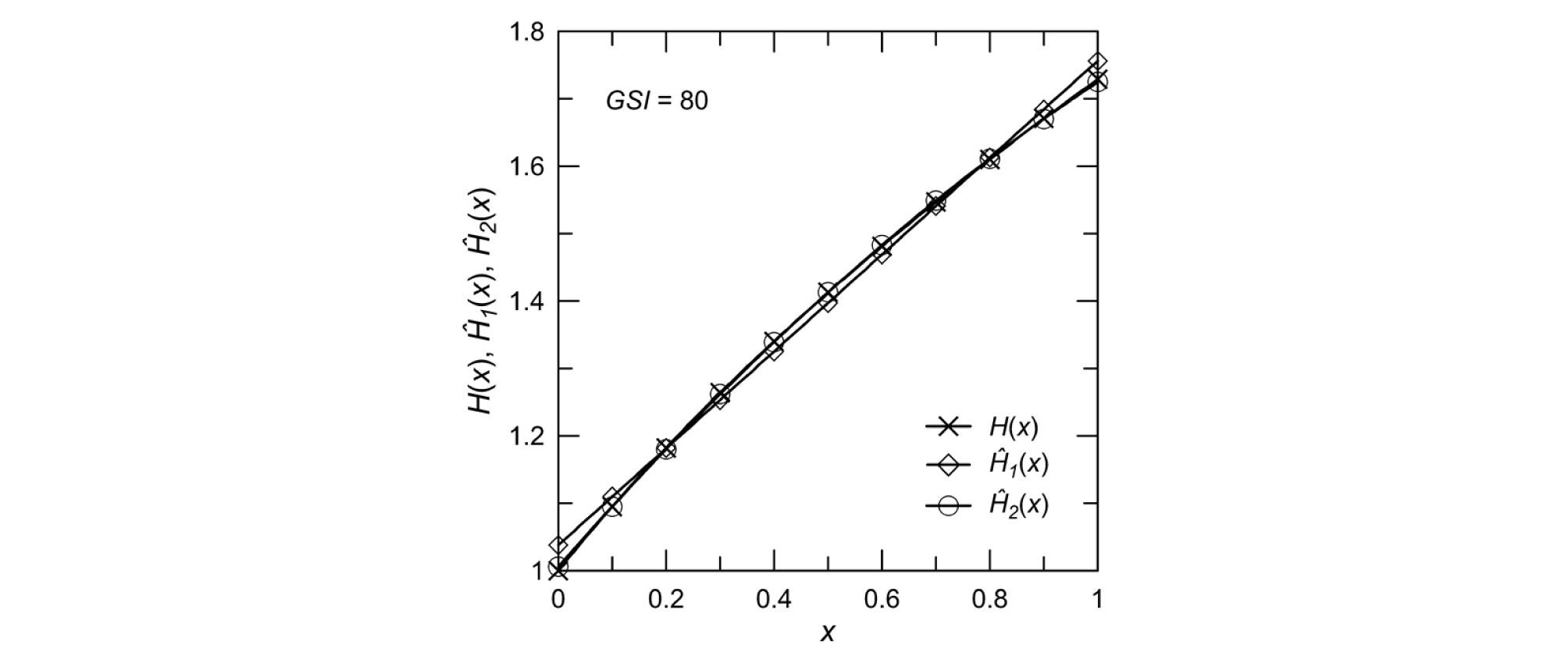
Fig. 3은 GSI=80을 가정한 후 과 를 H(x)와 비교 도시한 것으로 2차 다항식 최적 근사식 는 H(x)와 거의 일치함을 잘 보여준다. 이 때 과 는 연속인 비선형함수 H(x)에 대한 1차 및 2차 다항식 최소자승 근사에 해당한다.
3.3 근사 GHB Mohr 파괴포락선
식 (10)의 H(x) 대신 근사식 을 적용하면 다음과 같은 2차 방정식을 얻을 수 있다.
| $$12\omega_2\;x^2+(\omega_1-18\omega_2+\widetilde P)x+(6\omega_2-\omega_1)=0$$ | (23) |
식 (23)의 해는 식 (24)과 같다.
| $$x=\frac{(18\omega_2-\omega_1-\widetilde P)+\sqrt{(\omega_1-18\omega_2+\widetilde P)^2-48\omega_2(6\omega_2-\omega_1)}}{24\omega_2}$$ | (24) |
반면 식 (10)의 H(x) 대신 근사식 을 적용하면 다음과 같은 3차 방정식을 얻을 수 있다.
| $$x^3+\alpha_1x^2+\alpha_2x+\alpha_3=0$$ | (25) |
여기서
| $$\alpha_1=\frac{\omega_2-30\omega_3}{15\omega_3}$$ | (26) |
| $$\alpha_2=\frac{\omega_1-18\omega_2+210\omega_3+\widetilde P}{180\omega_3}$$ | (27) |
| $$\alpha_3=\frac{-\omega_1+6\omega_2-30\omega_3}{180\omega_3}$$ | (28) |
3차방정식, 식 (25)의 해는 다음과 같다.
| $$x=\frac23\sqrt{\alpha_1^2-3\alpha_2}\;\cos\left(\frac\theta3+\frac{4\mathrm\pi}3\right)-\frac{\alpha_1}3$$ | (29) |
여기서
| $$\theta=\cos^{-1}\left[\frac{9\alpha_1\alpha_2-27\alpha_3-2\alpha_1^3}{2(\alpha_1^2-3\alpha_2)^{3/2}}\right]$$ | (30) |
그러므로 식 (7)과 식 (9)를 상기하면 GHB 파괴기준식의 Mohr 파괴포락선 근사식은 H(x)의 최적 직선근사 또는 최적 2차 다항식 근사를 기반으로 하는 근 x 즉, 식 (24)와 식 (29)을 이용하여 식 (31)과 같은 해석적 수식으로 표현할 수 있다.
| $$\tau=m_b^{a/(1-a)}\sigma_{ci}\left(\frac a2\right)^{a/(1-a)}\;\frac{\sqrt{1-x^2}}2\left(\frac{1-x}x\right)^{a/(1-a)}$$ | (31) |
또한 접선마찰각(∅i)과 접선점착력(ci)는 근 x를 이용하여 다음 식 (32, 33)과 같이 계산할 수 있다.
| $$\varnothing_i=\sin^{-1}(x)$$ | (32) |
| $$c_i=\tau-\sigma\;\frac x{\sqrt{1-x^2}}$$ | (33) |
4. 근사 Mohr 파괴포락선식의 정확성 검증
3절에서 유도한 근사 GHB Mohr 파괴포락선식 (31)의 신뢰성을 검증하기 위하여 식 (31)로 계산한 전단강도를 정해(exact solution)와 비교하였다. 여기서 정해는 식 (10)의 해 x를 수치해석적으로 직접 구한 다음 이를 식 (31)에 대입하여 계산한 전단강도를 의미한다. 반면에 근사 전단강도는 식 (24) 또는 식 (29)를 이용하여 구한 x 값을 식 (31)에 대입하여 계산한 것이다.
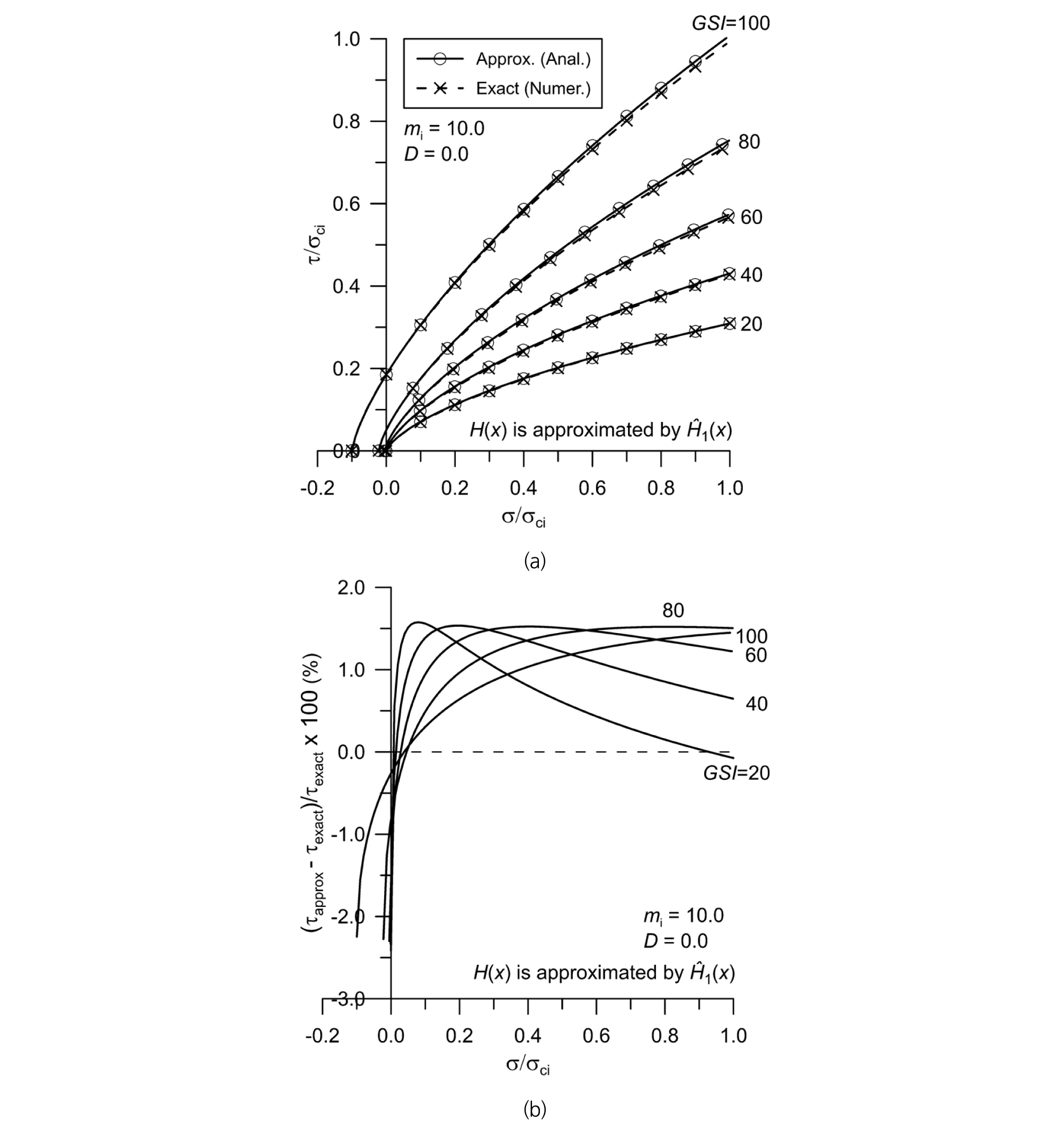
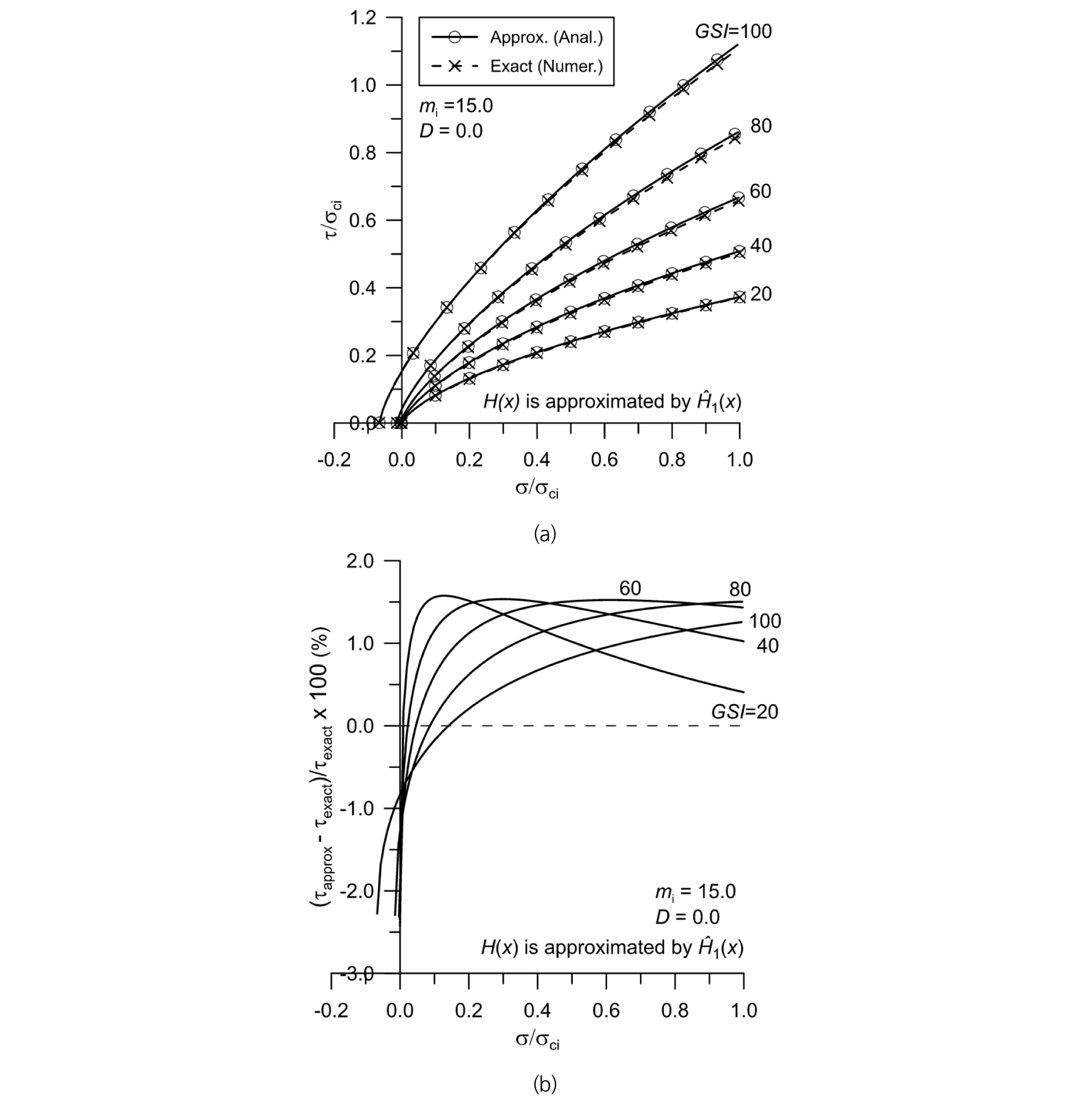
Fig. 4는 H(x)의 1차 다항식 최적 근사를 통해 유도한 Mohr 파괴포락선을 정해와 비교하고 전단강도 예측오차를 분석한 것이다. 여기에서는 mi=10, D=0을 가정하였고, 5가지 GSI 값 즉, 20, 40, 60, 80, 100이 고려되었다. 검증에서 고려한 전체 GSI 값에 대해 수직응력 범위 0≤σ/σci≤1에서 근사 Mohr 파괴포락선식으로 예측한 전단강도는 1.45% 오차 이내로 정해에 매우 근사함을 잘 보여준다. Fig. 5는 mi=15, D=0을 가정한 경우로서 mi=10인 경우와 유사한 정확성을 보여준다. 또한 Fig. 4(b)와 Fig. 5(b)에서 볼 수 있듯이 수직응력이 0에 가까운 경우를 제외하면 근사 Mohr 파괴포락선식이 정해보다 전단강도를 약간 크게 예측하는 특징을 나타낸다는 것을 알 수 있다.
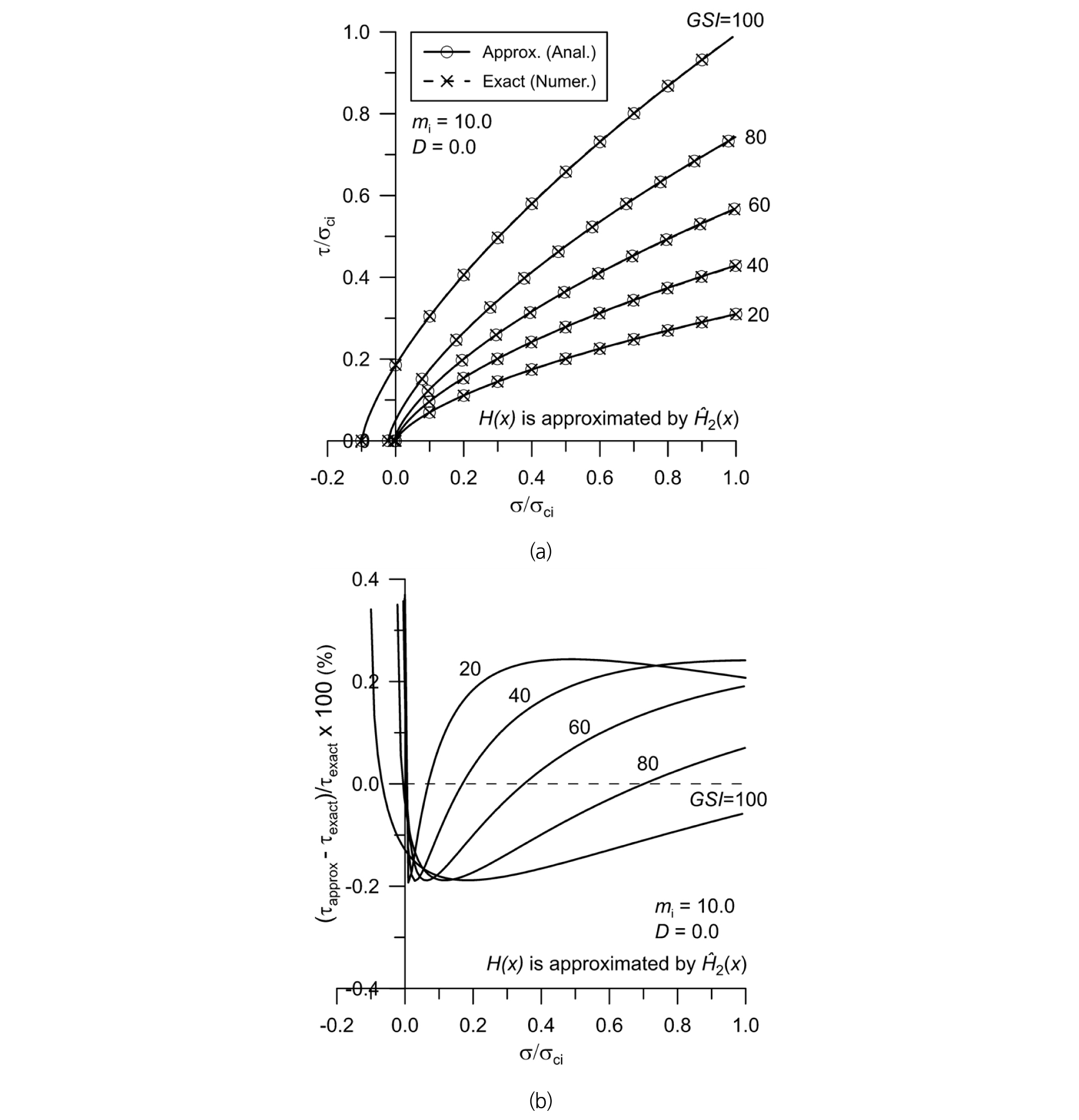
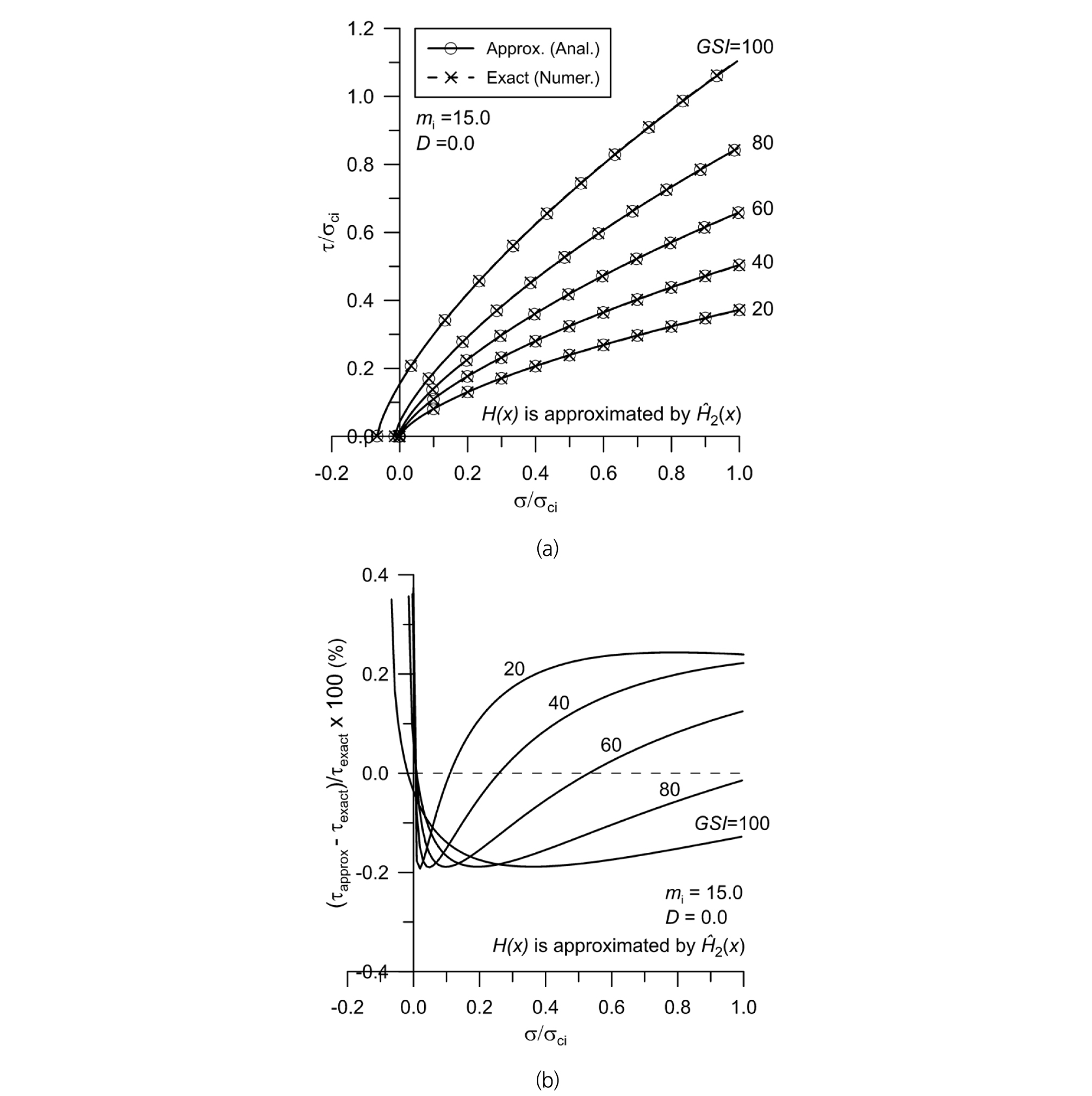
Fig. 6과 Fig. 7은 각각 Fig. 4 및 Fig. 5와 동일한 암반조건에서 H(x)의 2차 다항식 최적 근사를 통해 유도한 Mohr 파괴포락선의 정확성을 분석한 것이다. Fig. 6(a)과 Fig. 7(a)에서 볼 수 있는 것처럼 근사 Mohr 파괴포락선식으로 계산한 전단강도는 정해와 거의 구분이 되지 않을 정도로 정밀한 값임을 알 수 있다. 또한 H(x)의 2차 다항식 최적근사를 기반으로 유도한 Mohr 파괴포락선은 수직응력 범위 0≤σ/σci≤1에서 전단강도 예측오차 0.25% 이내로 정확하다는 것을 Fig. 6(b)과 Fig. 7(b)에서 확인할 수 있다. 또한 GSI 값이 100에 가까운 양호한 암반의 경우 전단강도 근사 예측값은 정해보다 약간 작으며 GSI 값이 작아질수록 정해보다 약간 큰 특징을 보여준다.
이상의 검증결과는 이 연구에서 유도한 해석적 근사 Mohr 파괴포락선식이 암반의 양호도와 암반 강도지수 값의 크기에 상관없이 정해에 매우 근사한 전단강도값을 계산한다는 사실을 확인시켜준다.
5. 요약 및 결론
GHB 암반파괴조건식은 암반공학적 적용을 목적으로 개발된 비선형 함수로서 최근 암반의 표준 파괴조건식으로 자리잡아가고 있다. 구속압의 증가에 따른 파괴강도 증가의 비선형성을 잘 반영한다는 점과 GSI 지수를 이용하여 무결암의 강도를 현장 암반의 강도로 보정하는 체계적인 방법을 제공한다는 측면에서 GHB 파괴함수는 현장 적용성이 뛰어난 파괴함수로 평가받고 있다. 그러나 파괴면의 전단강도를 파괴면에 작용하는 수직응력의 명시적 함수 즉, Mohr 파괴포락선을 해석적 수식으로 표시할 수 없다는 점이 GHB 파괴함수의 적용범위 확대를 제약하는 주요 요인이 되고 있다. GHB 파괴함수가 갖는 이러한 한계를 극복하기 위하여 이 연구에서는 임의의 비선형 연속함수를 다항함수(polynomial function)로 최적 근사시키는 수학적 기법을 도입하여 GHB 파괴함수의 근사 Mohr 파괴포락선을 유도하는 새로운 접근법을 제시하였고 그 정확성을 검증하였다.
이 연구에서 얻은 주요 결론은 다음과 같다.
1. 무차원 GHB 파괴조건식에 내포된 수직응력-접선마찰각 관계곡선은 0≤sin ∅i≤1 범위에서 곡률이 매우 작은 부드러운 곡선이므로 이 곡선을 1차 혹은 2차 다항식으로 최적 근사시킬 수 있음을 확인하였다.
2. 수직응력-접선마찰각 관계곡선을 1차 혹은 2차 다항식으로 최적 근사시킬 경우 접선마찰각을 수직응력의 명시적 함수로 표시할 수 있으며 그 결과를 전단응력 – 접선마찰각 관계식에 대입함으로써 근사적 GHB Mohr 파괴포락선을 유도하는 새로운 Mohr 파괴포락선 유도방법이 개발되었다.
3. mi=10, 15, D=0 인 경우, 1차 다항식 최적 근사를 기반으로 유도한 Mohr 파괴포락선의 전단강도 예측오차는 일축압축강도보다 작은 압축 수직응력의 범위에서 1.45% 이내였으나, 2차 다항식 최적 근사를 기반으로 한 경우는 0.25% 이내로 전단강도 예측 성능이 대폭 개선됨을 확인하였다.
4. 1차 및 2차 다항식 최적 근사를 기반으로 유도한 근사 Mohr 파괴포락선은 GSI 값 전 범위에서 정해와 매우 근사하다는 것이 확인되었다. 특히 2차 다항식 최적 근사를 기반으로 유도한 근사 Mohr 파괴포락선은 정해와 구분이 힘들 정도의 근사성을 보여 주었다.
5. 이 연구에서 개발된 근사 Mohr 파괴포락선은 GHB 파괴조건을 따르는 암반의 한계해석, 한계평형해석, 암반블록의 비선형 미끄러짐 해석 등에 활용이 가능하므로 이 연구결과는 GHB 파괴함수의 적용범위를 확대시키는 데 크게 기여할 것으로 예상된다.