1. 서 론
2. GHB 파괴조건식을 활용한 등가 M-C 강도정수 산정
2.1 GHB 암반파괴조건
2.2 등가 M-C 강도정수
3. 임의 최소주응력 구간에서 점착력과 마찰각의 최적 근사
3.1 수학적 방법론
3.2 정사영 원리를 이용한 곡선식의 최적 직선 근사
4. 압축 주응력이 작용하는 원형터널 주변 암반의 등가마찰각 및 등가점착력 계산
5. 결 론
1. 서 론
암반 파괴기준식은 응력의 함수로 표현되며 주어진 응력조건이 암반의 파괴를 발생시킬 수 있는지 여부를 판단하는 목적으로 사용된다. Mohr-Coulomb(M-C) 식과 Hoek-Brown(H-B) 식은 대표적인 암반의 파괴함수이다. M-C 파괴기준식은 마찰각(friction angle)과 점착력(cohesion)으로 정의되는 선형 함수이다. 반면에 H-B 식은 강도정수 m, s 및 무결암 일축압축강도 σci로 정의되는 비선형 함수이다(Hoek, 1983). 선형 M-C식이 현장 기술자들에게 익숙하며 수치해석적 활용 측면에서 간편하다는 장점은 있지만 암반강도의 비선형 특성을 고려하지 못하며 인장강도를 비현실적으로 높게 산정한다는 단점 또한 무시할 수 없다. H-B 식은 암반공학적 활용에 특화된 파괴기준식이고 암반강도를 상대적으로 더 정확히 산정하지만 비선형 함수이므로 적용에 어려움이 따른다.
암반의 파괴강도를 정확히 평가하기 위해서는 현장 조건을 고려한 강도정수의 결정이 무엇보다도 중요하다. 암반의 마찰각과 점착력을 직접 측정하는 것이 쉽지 않으므로 M-C 파괴기준식을 적용하는 경우 경험적 방법들이 마찰각과 점착력 산정에 많이 활용되고 있다. 예를 들어 공학적 암반분류 결과를 활용하는 경험적 가이드라인(Bieniawski, 1989)이 제시되어 있지만 이는 암반분류 기술자의 숙련도 및 주관에 따라 M-C 강도정수의 평가결과가 달라질 수 있는 접근법이다. 반면에 2002년 개정 발표된 H-B 식 즉, GHB 식(Generalized Hoek-Brown criterion, Hoek et al., 2002)에서는 GSI 지수(Geological Strength Index, Hoek & Marinos, 2000)를 도입하여 암반의 상태를 고려한 강도정수 산정과정을 체계화시켰다. 오늘날 GHB 파괴조건식은 표준 암반파괴조건식의 하나로 인정받고 있는 추세이며 단순한 파괴강도 추정에 활용되는 것 외에도 GHB 파괴함수를 항복함수로 활용한 탄소성 구성방정식 개발(Clausen & Damkilde, 2008, Sørensen et al., 2015), 한계해석법(limit analysis)이나 유한요소법을 기반으로 한 암반기초 지지력 평가(Saada et al., 2011, Mansouri et al., 2019)와 사면안전율 계산(Xu & Yang, 2018) 등에 활발히 적용되고 있다.
GHB 파괴기준식은 되도록 본래의 비선형 함수 형태로 직접 활용하여야 하지만 암반공학적 수치해석 과정에서 여전히 M-C 파괴함수의 활용 빈도가 높음을 고려하여 GHB 파괴기준식에 최적 근사하는 M-C 식의 등가마찰각과 등가점착력을 해석적으로 계산하는 수식이 GHB 파괴기준식의 발표와 함께 제안되었다(Hoek et al., 2002). 그러나 Hoek et al.(2002)에서 제안된 등가마찰각과 등가점착력 계산식은 암반의 인장강도를 하한 값으로 선정한 최소주응력의 범위를 가정하고 있으므로 인장응력이 분포하지 않는 해석영역에 적용할 경우 이 식에 의한 등가마찰각과 등가점착력 산정결과는 정확성이 떨어질 가능성이 있다.
Hoek et al.(2002)에서 제시된 등가마찰각과 등가점착력 계산식이 갖는 이러한 단점을 보완하기 위해 이 연구에서는 임의로 설정한 최소주응력 구간에서 GHB 파괴기준식에 최적 근사하는 M-C식의 등가마찰각과 등가점착력을 계산하는 해석적 수식을 유도한 후, 결과식의 정확성을 검증하였다. Sofianos & Nomikos(2006)도 유사한 연구결과를 발표하였지만 해석적 결과식이 매우 복잡하며 결과식의 유도과정을 명시적으로 제시하지 못하였다. 반면에 이 연구에서는 응력 무차원화 변환(Rojat et al., 2015) 과정을 거쳐 단순화시킨 GHB 파괴기준식을 상수와 1차 함수를 원소로 하는 선형 함수공간에 정사영 시키는 대수학적 원리(Bretscher, 2005)를 적용함으로써 결과식 유도과정을 단순화시켰고, 유도된 결과식의 수학적 엄밀성을 확보하였다.
2. GHB 파괴조건식을 활용한 등가 M-C 강도정수 산정
2.1 GHB 암반파괴조건
절리 암반의 파괴개시 조건으로 개발된 GHB 파괴조건식에서는 최소주응력이 σ3 일 때 최대주응력 σ1이 다음의 비선형 관계식을 만족하면 암반의 파괴가 발생하는 것으로 가정한다(Hoek et al., 2002).
| $$\sigma_1=\sigma_3+\sigma_{ci}\;\left(m_b\frac{\sigma_3}{\sigma_{ci}}+s\right)^a$$ | (1) |
식 (1)에서 σci는 무결암의 일축압축강도이며, 암반 강도정수 mb, s와 상수 a는 다음의 경험식들을 이용하여 계산하는 것이 제안되었다.
| $$m_b=m_i\;\exp\;\left(\frac{GSI-100}{28-14D}\right)$$ | (2) |
| $$s=\exp\;\left(\frac{GSI-100}{9-3D}\right)$$ | (3) |
| $$a=0.5+(1/6)\;\left(e^{-GSI/15}-e^{-20/3}\right)$$ | (4) |
여기서 mi는 암종과 암석입자의 분포특성(texture)을 반영하는 무결암의 강도정수이다(Hoek & Brown, 1997). 또한 GSI는 절리면의 상태와 절리분포의 구조적 특징을 반영하여 계산되는 0과 100 사이의 값으로 100에 가까울수록 우수한 암반조건을 의미한다. Hoek & Marinos(2000)에 의해 GSI 지수 산정을 위한 도표가 개발된 이 후 GSI 지수의 적용범위를 넓히기 위해 더욱 개선된 도표가 제안되었으며(Marinos et al., 2007), GSI 지수 산정의 객관성을 높이기 위해 기존의 암반분류변수를 활용하는 연구도 시도되었다(Hoek et al., 2013). 한편, 식 (2)와 식 (3)에서 교란지수 D는 0과 1 사이의 값으로 발파손상이나 암반 굴착면 주변의 응력이완이 원인이 되어 발생한 암반교란 정도를 반영하며 1에 가까운 값일수록 암반이 더 심하게 교란되었음을 의미한다.
2.2 등가 M-C 강도정수
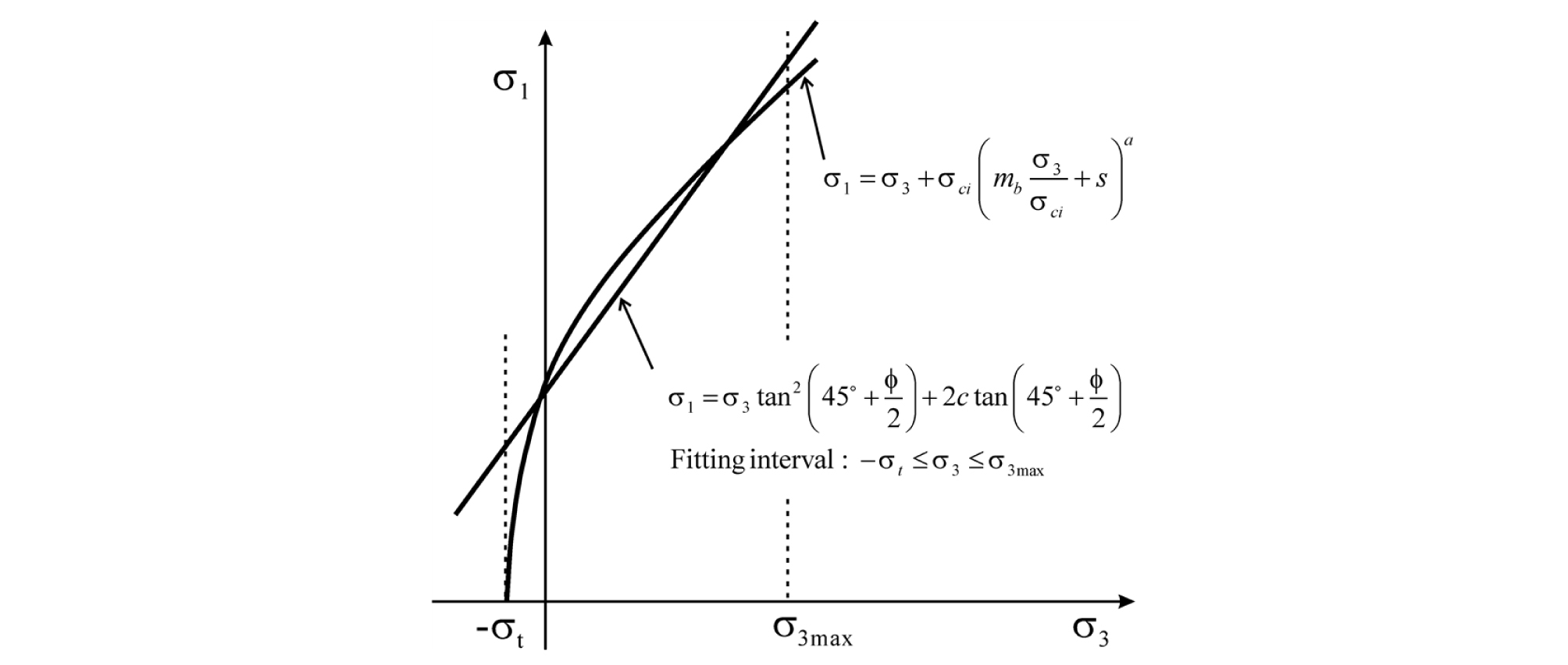
현장 기술자들이 마찰각과 점착력으로 암반강도를 표현하는 것에 익숙하고 또 많은 암반공학 소프트웨어들이 선형 M-C 파괴기준식을 채택하고 있음을 고려하여 GHB 파괴기준식으로부터 근사적으로 마찰각과 점착력을 산정하는 방법이 GHB 파괴기준식의 발표와 함께 제안되었다(Hoek et al., 2002). 이들에 따르면 Fig. 1과 같이 최소주응력(σ3)의 범위를 인장강도(σt)와 임의 상한 값(σ3max) 사이로 한정할 때 범위 -σt≤σ3≤σ3max에서 비선형 GHB 파괴기준식을 최적 선형 근사하는 점착력(c)과 마찰각(∅)은 다음 식과 같이 주어진다.
| $$\varnothing=\sin^{-1}\;\left[\frac{6am_b\;\;{(s+m_b\sigma_{3n})}^{a-1}}{2(1+a)(2+a)+6am_b\;{(s+m_b\sigma_{3n})}^{a-1}}\right]$$ | (5) |
여기서 σ3n=σ3max/σci이다.
식 (5)과 식 (6)은 비선형 GHB 파괴함수와 선형 M-C 파괴함수의 교차로 형성되는 상하 영역의 면적이 영역 -σt≤σ3≤σ3max에서 같다는 조건을 적용하여 유도된 것이다. 터널 해석의 경우 σ3max 추정식은
| $$\frac{\sigma_{3max}}{\sigma_{cm}}=0.47\;\left(\frac{\sigma_{cm}}{\gamma H}\right)^{-0.94}$$ | (7) |
이며, 암반사면 해석의 경우 σ3max 추정식은
| $$\frac{\sigma_{3max}}{\sigma_{cm}}=0.72\;\left(\frac{\sigma_{cm}}{\gamma H}\right)^{-0.91}$$ | (8) |
으로 제안되었다(Hoek et al., 2002). 식 (7)은 터널 주변에 형성된 파쇄대가 지표면까지 확장된 경우를 제외한 모든 터널에 적용할 수 있다. 식 (7)과 식 (8)에서 γ는 암반의 단위중량(MPa/m)이며, H(m)는 각각 터널심도와 사면의 높이이다. 터널해석의 경우 수평지압이 연직지압보다 클 때는 수평지압이 γH을 대신한다. σcm은 암반의 일축압축강도로서 σ3max=σci/4를 가정하고 식 (5)와 식 (6)으로 계산한 마찰각과 점착력을 M-C 파괴조건식의 일축압축강도 이론식 2ccos𝜙/(1-sin𝜙)에 대입하여 유도한 다음 식으로 계산한다.
| $$\frac{\sigma_{cm}}{\sigma_{ci}}=\frac{\left[m_b+4s-a(m_b-8s)\right]{\displaystyle\;}{\displaystyle{\displaystyle\left(\frac{m_b}4+s\right)}^{a-1}}}{2(1+a)(2+a)}$$ | (9) |
그러나 식 (5)과 식 (6)은 최소주응력이 인장응력일 경우를 포함한 구간 -σt≤σ3≤σ3max에서 비선형 GHB 파괴조건식을 선형 M-C 파괴조건식으로 최적 근사시킨 결과이므로 압축응력만 작용하는 암반에 적용할 경우 점착력은 과소평가되고 마찰각은 과대평가될 수 있다. 이 연구에서는 식 (5)과 식 (6)의 이러한 단점을 극복하기 위해 최소주응력의 임의 구간에서 선형 M-C 파괴기준식을 GHB 파괴기준식에 최적 근사시켜 점착력과 마찰각을 해석적으로 계산하는 방법을 제시하였다. 관련된 해석적 수식들의 유도를 위한 수학적 방법론과 결과식들의 유도과정이 3절에서 자세히 설명되었다.
3. 임의 최소주응력 구간에서 점착력과 마찰각의 최적 근사
3.1 수학적 방법론
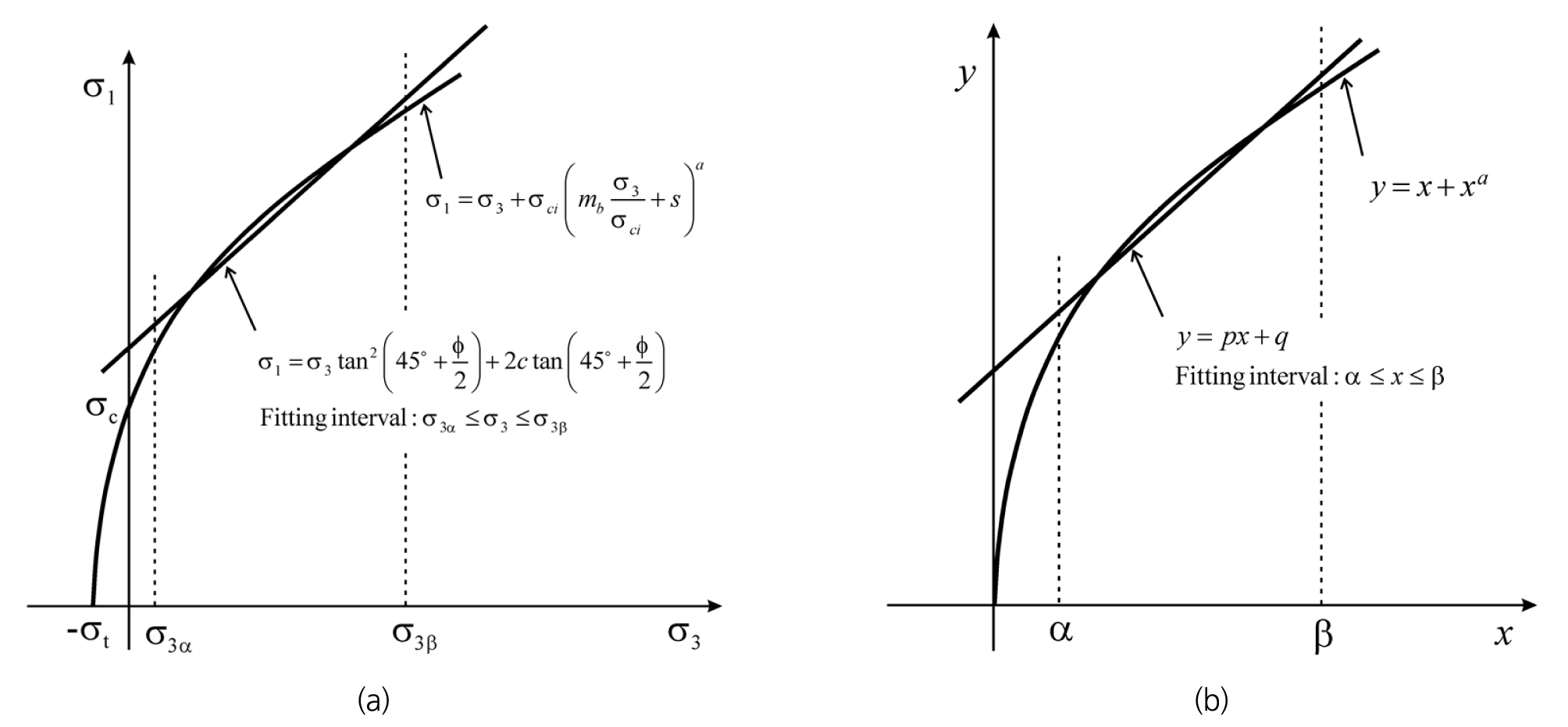
이 연구에서는 Fig. 2(a)에 표시한 것처럼 임의 구간 σ3α≤σ3≤σ3β에서 GHB 파괴기준식을 최적 근사하는 M-C 파괴기준식을 해석적 수식으로 표현하였다. 이 목적을 위해 GHB 파괴기준식 (1)을 직접 활용할 경우 수학적 유도과정이 복잡해지는 것을 피할 수 없다. 그러나 Rojat et al.(2015)이 처음 제안하였고, Lee & Pietruszczak(2017)와 Lee(2018)에서 활용된 응력 무차원화 변환을 이용하면 GHB 파괴기준식을 다음과 같이 단순화시킬 수 있다.
| $$y\;=\;x\;+\;x^a$$ | (10) |
여기서
| $$y=\;\frac1{m_b^{1/(1-a)}}\;\left(m_b\frac{\sigma_1}{\sigma_{ci}}+s\right)$$ | (11) |
| $$x=\;\frac1{m_b^{1/(1-a)}}\;\left(m_b\frac{\sigma_3}{\sigma_{ci}}+s\right)$$ | (12) |
x-y 직교 좌표계에서 식 (10)은 Fig. 2(b)와 같이 원점을 지나는 곡선이다. σ3α와 σ3β에 대응하는 무차원 변환 응력값을 각각 α와 β라 하면
| $$\alpha=\frac1{m_b^{1/(1-a)}}\;\left(m_b\frac{\sigma_{3\alpha}}{\sigma_{ci}}+s\right),\;\;\beta=\frac1{m_b^{1/(1-a)}}\;\left(m_b\frac{\sigma_{3\beta}}{\sigma_{ci}}+s\right)$$ | (13) |
이므로 구간 σ3α≤σ3≤σ3β에서 GHB 파괴기준식에 최적 근사하는 M-C 파괴기준식을 구하는 문제는 무차원 최소주응력 구간 α≤x≤β에서 식 (10)에 최적 근사하는 직선 식을 찾는 문제로 귀착된다. 이 연구에서는 곡선 함수를 선형 다항함수(polynomial function) 공간으로 정사영(orthogonal projection)시키는 선형대수학적 원리를 적용하여 임의 구간 σ3α≤σ3≤σ3β에서 GHB 파괴기준식을 최적 근사하는 M-C 파괴기준식을 유도하였다.
3.2 정사영 원리를 이용한 곡선식의 최적 직선 근사
폐구간 [α, β]에서 상수를 포함한 연속인 모든 1차 함수를 원소로 하는 선형 내적공간(linear inner product space)을 V[α, β]이라 하면 V의 원소인 두 함수 f와 g의 내적은 다음과 같이 정의할 수 있다.
| $$<f,\;g>=\int_\alpha^\beta\;f(x)\;g(x)\;dx\;\;\;\;\;\;\;\;\;\;\;\;f,\;g\;\in\;V$$ | (14) |
또한 식 (14)의 함수내적 정의를 이용하여 함수 f(x)의 놈(norm) ∥f∥은 다음과 같이 계산할 수 있다.
| $$\parallel f\parallel=\sqrt{<f,\;f>}=\sqrt{\int_\alpha^\beta f^2(x)\;dx}$$ | (15) |
한편, 선형공간 V[α, β]을 생성(span)하는 정규직교 기저(orthonormal basis)는 다음의 두 함수로 이루어진다.
| $$u_1(x)=\frac1{\sqrt{\beta-\alpha}},\;\;\;\;\;\;\;\;\;u_2(x)=\;\sqrt{\frac{12}{{(\beta-\alpha)}^3}}\;\left(x-\frac{\alpha+\beta}2\right)$$ | (16) |
식 (16)의 u1과 u2는 ∥u1∥=∥u2∥=1이고 < u1, u2 > = 0임을 보일 수 있다.
이제 폐구간 [α, β]에서 식 (10)을 최적 근사하는 직선 식을
| $$y=px+q$$ | (17) |
이라 하면 이 직선 식은 식 (10)을 선형공간 V[α, β]에 정사영시킨 결과이며 다음과 같이 표시된다.
| $$y=<u_1,\;(x+x^a)>\;u_1+<u_2,\;(x+x^a)>u_2$$ | (18) |
따라서 최적 직선 식의 기울기 p와 y축 절편값 q는 다음과 같이 해석적 수식으로 표현된다.
| $$p=1+\frac6{(a+1)(a+2)}\frac{\alpha\;(\beta^{a+2}-\alpha^{a+2})-(a+2)\;(\alpha\;\beta^{a+1}-\beta\alpha^{a+1})}{{(\beta-\alpha)}^3}$$ | (19) |
| $$q=\frac1{(a+1)}\frac{\beta^{a+1}-\alpha^{a+1}}{\beta-\alpha}-\frac{3(\beta+a)}{(a+1)(a+2)}\frac{\;a(\beta^{a+2}-\alpha^{a+2})-(a+2)(\alpha\beta^{a+1}-\beta\alpha^{a+1})}{{(\beta-\alpha)}^3}$$ | (20) |
응력무차원화 변환식 식 (11)과 식 (12)을 상기하면 식 (17)은
이므로 구간 σ3α≤σ3≤σ3β에서 GHB 파괴기준식에 최적 근사하는 M-C 식을 다음과 같이 얻을 수 있다.
| $$\sigma_1=p\;\sigma_3+\left[(p-1)\frac s{m_b}+q\;m_b^{a/1-a}\right]\;\sigma_{ci}$$ | (22) |
식 (22)에서 p는 σ3 - σ1 공간에서 M-C 파괴기준식의 기울기와 동일하므로
| $$p=\tan^2\;\left(45^\circ+\frac\varnothing2\right)=\frac{1+\sin\varnothing}{1-\sin\varnothing}$$ | (23) |
임을 알 수 있다. 따라서 구간 σ3α≤σ3≤σ3β에서 최적 근사 마찰각은 다음과 같은 해석적 수식으로 표시할 수 있다.
| $$\varnothing=\sin^{-1}\left(\frac{p-1}{p+1}\right)$$ | (24) |
한편, 식 (22) 우변의 두 번째 항은 일축압축강도 즉, 2c tan (45°+𝜙/2)이므로 구간 σ3α≤σ3≤σ3β에서 최적 근사 점착력은 다음과 같은 해석적 수식으로 표시할 수 있다.
| $$c=\frac{\sigma_{ci}}{2\sqrt p}\left[(p-1)\frac s{m_b}+q\;m_b^{a/1-a}\right]$$ | (25) |
σ3α=-sσci / mb = -σt 일 때 α=0이므로 σ3α= -sσci / mb, σ3β = σ3max인 경우 식 (24)와 식 (25)는 각각 식 (5), 식 (6)과 정확히 일치함을 보일 수 있다.
이 연구에서 유도된 최적 근사 M-C 파괴기준식의 정확성은 식 (19)의 극한값 계산을 통해서도 확인할 수 있다. 로피탈(L’Hospital)의 정리를 이용하면 β → α일 때 p의 극한값은 다음과 같이 계산된다.
| $$\lim_{\beta\rightarrow\alpha}p=1+a\;\alpha^{a-1}=1+a\;m_b\;\left(m_b\frac{\sigma_{3\alpha}}{\sigma_{ci}}+s\right)^{a-1}$$ | (26) |
식 (26)의 결과는 식 (1)을 직접 이용하여 σ3 = σ3α에서 구한 접선기울기 값 과 정확히 일치함을 알 수 있다.
4. 압축 주응력이 작용하는 원형터널 주변 암반의 등가마찰각 및 등가점착력 계산
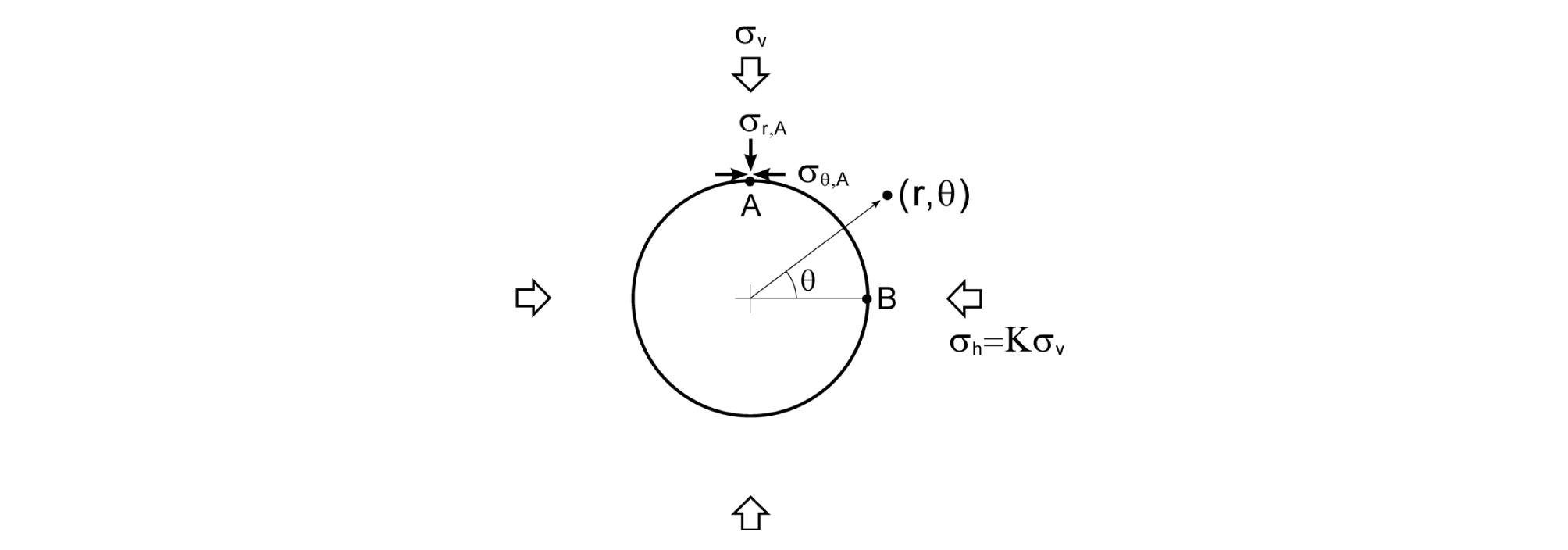
GHB 파괴기준식을 따르는 암반의 등가마찰각 및 등가점착력을 계산하기 위해 Hoek et al.(2002)이 제안한 식 (5)과 식 (6)은 선형 M-C 파괴기준식을 최소주응력 구간 -σt≤σ3≤σ3max에서 GHB 파괴기준식에 최적 근사시킨 결과이다. 그러므로 해석영역에 인장응력이 분포하지 않는 경우, 이 식들에 의해 산정된 등가마찰각과 등가점착력은 암반의 강도특성을 적절히 반영하지 못할 가능성이 있다. 예를 들어 Fig. 3과 같이 측압비가 K=σh / σv인 2축 응력장이 형성된 탄성 암반 내에 원형터널이 굴착될 경우 점 A와 점 B에서 발생되는 접선응력은 각각 σθ,A = (3K-1) σv , σθ,B = (3K) σv 이므로 1/3 < K < 3이면 터널 벽면에 인장응력이 유도되지 않는다. 이 경우 터널벽면에서 최소주응력 값이 0임을 고려할 때 최소주응력 구간 0≤σ3≤σ3max에서 최적 등가마찰각과 등가점착력을 산정하는 것이 더 합리적인 방법이 될 수 있다.
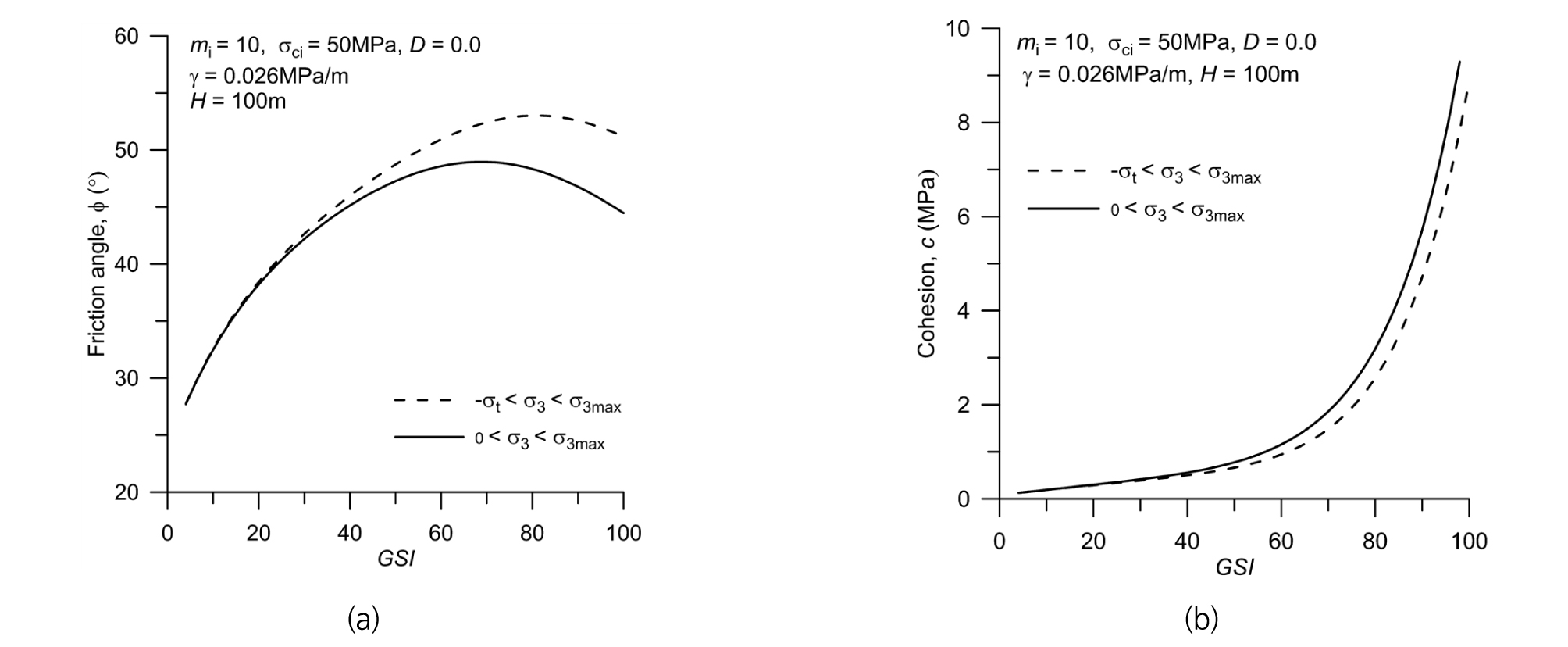
이 연구에서는 원형터널 굴착을 가정한 후 구간 -σt≤σ3≤σ3max에 대한 최적 선형근사 결과인 식 (5) 및 식 (6)을 이용하여 계산한 등가마찰각과 등가점착력을 구간 0≤σ3≤σ3max일 때 식 (24)와 식 (25)을 이용하여 계산한 결과와 비교하였다. GSI 값의 변화에 따라 두 방법에 의해 계산한 등가마찰각과 등가점착력의 변화 추이를 Fig. 4에 도시하였다. 터널의 심도는 100m로 가정하였으며, 나머지 입력자료는 mi = 10, σci = 50MPa, D = 0.0, γ = 0.026 MPa/m을 가정하였다. 최소주응력의 범위를 압축응력으로 한정할 경우 Hoek et al.(2002)의 제안식을 이용하여 계산한 결과와 비교하여 등가마찰각은 낮게 산정되며, 점착력은 높게 산정됨을 볼 수 있다. 이는 동일한 σ3max에 대해 최소주응력의 범위를 압축응력으로 한정하면 무차원 응력좌표계 x-y에서 최적 근사 직선의 기울기는 상대적으로 낮아지고 y축 절편값은 상대적으로 증가하기 때문이다. 등가마찰각의 경우 GSI 값이 70 ~ 80 이상인 영역에서는 GSI 값이 증가할수록 즉, 암질이 우수할수록 오히려 감소하는 특징을 보여준다. 반면에 이 영역에서 등가점착력은 GSI 값의 증가와 더불어 급격한 증가를 보여주고 있다.
Fig. 5에서 볼 수 있듯이 0 < GSI < 50일 때 두 방법의 계산결과는 큰 차이를 보이지 않지만 이후 등가마찰각의 차이는 GSI 값의 증가와 더불어 꾸준히 증가한다. 0 < GSI < 50 일 때 두 방법에 의한 결과 차이가 미미한 것은 이 범위에서 GHB 파괴기준식이 예측하는 인장강도 크기가 매우 작기 때문으로 추측된다. 그림에서 𝜙GHB와 cGHB는 Hoek et al.(2002)의 제안식 즉, 식 (5)과 식 (6)으로 계산한 등가마찰각과 등가점착력을 의미하며 𝜙comp_σ3와 𝜙comp_σ3는 구간 0≤σ3≤σ3max에서 구한 등가 강도정수이다. GSI=100 일 때 등가마찰각 비는 𝜙comp_σ3 / 𝜙GHB ≈ 0.87 정도이다. 등가점착력의 차이 역시 GSI 값의 증가와 함께 증가하지만 GSI=72 일 때 ccomp_σ3 / cGHB ≈ 1.25에 도달한 이 후 GSI 값의 증가와 더불어 다시 소폭 감소하는 특징을 보여준다.
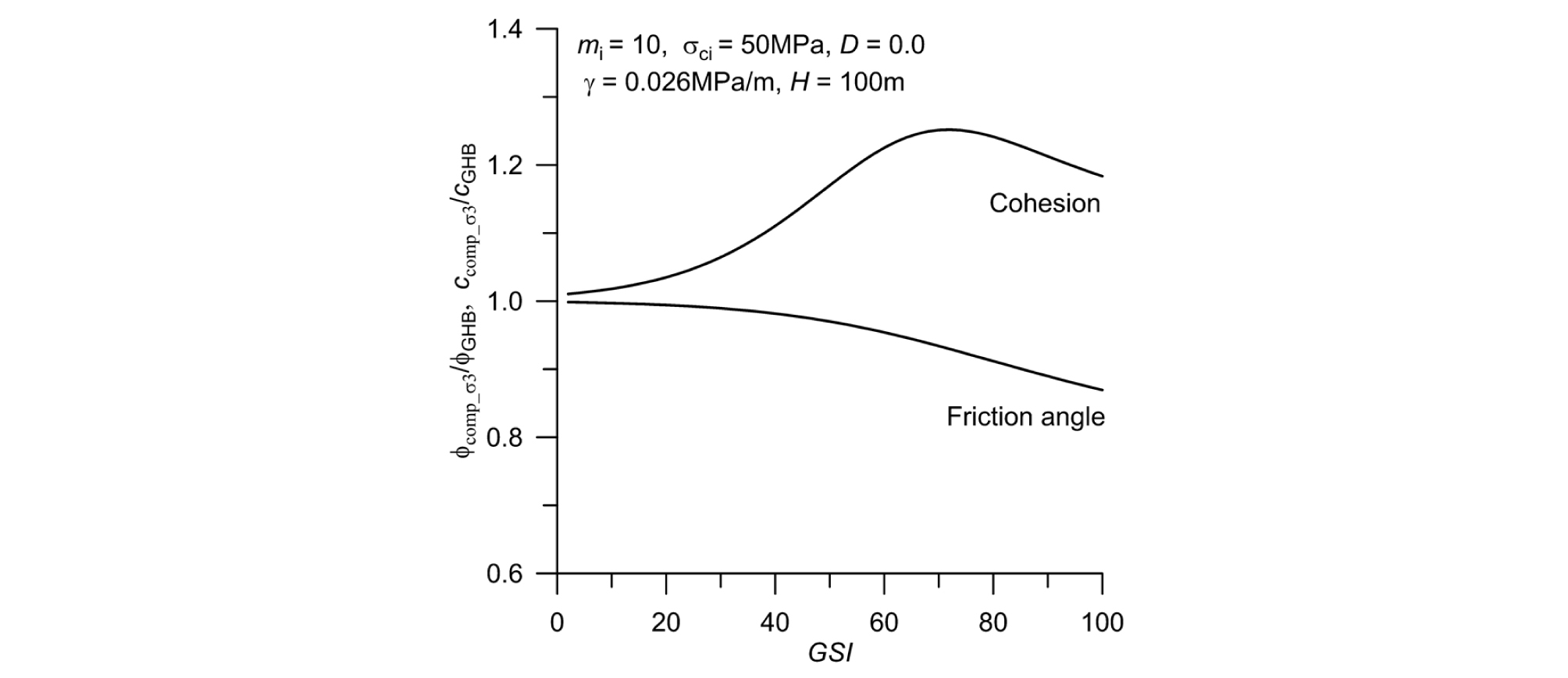
Fig. 5.
Ratios of the equivalent M-C parameter values to the equivalent values estimated by Hoek et al. (2002) for the range of compressive minor principal stress
지금까지 설명한 등가 M-C 강도정수 산정법 비교분석 결과는 이 연구에서 유도한 등가 M-C 강도정수 산정식, 즉 식 (24)과 식 (25)의 활용 가능성을 잘 보여준다. 해석영역의 최소주응력의 범위를 특정할 수 있을 경우 식 (24)과 식 (25)을 이용하여 등가마찰각과 등가점착력을 계산하면 Hoek et al.(2002)이 제안한 방법에 의한 것보다 더 정밀한 등가 M-C 강도정수의 산정이 가능할 것으로 판단된다.
5. 결 론
GHB 파괴기준식은 암반의 강도 비선형성을 표현할 수 있을 뿐만 아니라 현장의 암반조건을 고려하여 관련 강도정수를 산정하는 실용적 체계를 제공한다는 장점 때문에 표준 암반파괴기준식의 하나로 자리잡아가고 있다. 그러나 많은 현장기술자들이 여전히 암반의 강도를 마찰각과 점착력으로 표현하는 경우가 많고, 다수의 암반구조물 안정성 해석 소프트웨어들이 M-C식을 암반 파괴조건식으로 채용하고 있음을 고려할 때 GHB 파괴기준식으로부터 등가마찰각과 등가점착력을 산정하는 합리적인 해석적 수식이 함께 개발될 필요가 있다. 이 목적을 위해 Hoek et al.(2002)이 제안한 해석적 수식은 하한 값이 암반의 인장강도이고 상한 값이 터널해석과 사면해석의 경우에 각각 달리 설정되는 최소주응력 구간에서 비선형 GHB 파괴기준식에 최적 근사하는 선형 M-C 파괴기준식을 해석적으로 구한 결과이다. 그러나 Hoek et al.(2002)의 등가마찰각 및 등가점착력 계산식은 항상 인장강도를 하한으로 하는 최소주응력 구간을 가정하므로 인장응력이 분포하지 않는 해석영역의 등가 M-C 강도정수 산정에 활용될 경우 다소 부정확한 M-C 강도정수 산정결과를 얻을 수 있다. Hoek et al.(2002)의 등가마찰각 및 등가점착력 계산식이 갖는 이러한 단점을 개선시키기 위해 이 연구에서는 임의의 최소주응력 구간에서 GHB 파괴기준식에 최적 근사하는 M-C 기준식 즉, 최적 등가마찰각 및 등가점착력을 계산할 수 있는 해석적 수식을 유도하였다.
유도된 결과식에서 최소주응력의 상한 값을 하한 값에 점근시키면 최소주응력 하한 값에서 GHB 파괴기준식의 접선마찰각과 접선점착력이 얻어짐을 확인하였다. 또한 최소주응력 하한 값을 암반의 인장강도로 설정할 경우 이 연구에서 유도된 결과식은 Hoek et al.(2002)의 등가마찰각 및 등가점착력 계산식과 정확히 일치함을 확인하였다.
터널 해석의 경우를 가정하고 이 연구에서 유도한 해석적 수식을 이용하여 압축 최소주응력 구간에서 등가마찰각과 등가점착력을 계산한 후 그 결과를 Hoek et al.(2002)의 해석식을 이용한 결과와 비교하였다. GSI 값 전 범위에서 등가마찰각은 Hoek et al. (2002)의 해석식을 이용한 결과보다 낮게 계산되며, 등가점착력은 높게 계산되었다. 등가마찰각의 경우 최대 13% 정도 낮게 산정되었으며 등가점착력의 경우 최대 25% 정도 높게 산정되었다. 그러나 GSI 값이 50 이하인 비교적 불량한 암반에서는 두 방법에 의한 결과의 차이가 미미한 것으로 나타났다.
해석영역의 최소주응력 범위가 예측 가능한 경우 이 연구에서 유도한 등가마찰각 및 등가점착력 계산식을 이용하여 M-C 강도정수를 산정하면 Hoek et al.(2002)의 해석식을 이용한 경우보다 더 정밀한 암반 강도정수 산정이 가능할 것으로 판단된다.