1. 서 론

석회석은 국내생산광물에서 가장 큰 비중을 차지하는 비금속 광상 중의 하나이며, 환경문제로 시멘트 원료를 위한 노천채광을 제외하고는 대부분이 지하채광으로 전환되어 지하 갱도 및 채광장의 안정성 문제뿐만 아니라 채광 후 시간이 경과됨에 따라 지표침하 문제도 점차적으로 발생하고 있는 실정이다. 광산 현장에서는 광물의 품위에 따른 선택채광으로 복합적이고 체계적인 설계과정이나 방법을 적용하는 경우가 드물다. 또한 암반거동에 대한 예측이 어렵기 때문에 안정성문제로 어려움을 겪고 있다. 광산은 개발초기 시 안전할지라도, 광산운영 중 계속적인 채광으로 채굴적 체적이 증가되어 공동 주위의 응력집중과 크기가 변화된다. 이에 따라 공동주위에서 균열이 발생하고 국부적으로 천반이나 측벽으로부터의 불연속면들에 의해 형성된 쐐기들이 채광에 따른 발파진동 등에 의해 낙석이 발생하면서 넓은 범위의 파괴가 초래되어 불안정성 문제가 심각한 상태에 이르기도 한다. 광산에서 지하공동의 규격 결정이나 암반제어대책으로 사용할 수 있는 일반적인 방법이 없기 때문에 각 현장마다 상황에 따라 경험적으로 결정하거나 종종 여러 불확실성에 대한 해결책으로 암반분류법이 많이 사용되고 있다.

광산에서 갱도나 채굴적 안정성 평가를 위해서는 RMR(Bieniawski 1973, 1989)이나 Q시스템(Barton et al., 1974, 2002)과 같은 통상적인 암반분류법을 사용하거나 또는 광산 특수상황에 따른 경험적인 분류방법들이 기존의 분류법들을 근거로 하여 광산에 적용가능하도록 개선된 분류법들을 사용해왔다. 광산관련 암반분류법은 Laubscher(1977)가 RMR에 발파와 채광에 따른 절리방향, 풍화정도, 유도응력 및 응력변화 등을 고려한 MRMR(Mining Rock Mass Rating)을 처음으로 개발하였다. 또한 Laubscher (1984)는 MRMR를 이용하여 일축압축강도와 관련하여 설계 암반강도 개념을 도입하였고, Laubscher and Jakubec(2001)는 RQD를 제외하는 등 MRMR을 보완 수정하였다. 채광공동 설계 즉 갱도와 채굴적의 폭과 관련된 안정성 그래프(Stability graph)법을 Mathews et al.(1981)가 처음으로 제안하였지만. 초기 안정성 그래프법은 조사 자료수의 제한으로 후에 수정보완이 이루어졌다. 주방식 채광법에서 광주의 안전성에 대해 Esterhuizen et al.(2006)은 RMR을 사용하여 광주를 평가하였고, 광주에 대한 시각적인 광주분류를 시도하였다. 이와 달리 Q 시스템의 광산적용은 안정성 그래프법외에도 Mikula and Lee(2003)와 Peck and Lee(2007)등이 호주에서 지하 금속광산에 적용하였다. 국내에서는 광산을 대상으로 하는 암반분류의 적용이나 연구는 2000년대 초부터 석회석 광산을 대상으로 연구가 조금씩 수행되었지만(Sunwoo et al., 2003, 2005; Rao et al., 2003) 여전히 답보상태에 있다.

여기에서는 석회석 광산에서 무지보 갱도의 최대 갱도폭을 결정하기 위해 암반분류법 중에 Q 시스템(Barton et al., 1974, 2002)을 이용한 갱도폭의 결정에 대해 고찰하고자 한다. 이를 위해 국내 석회석 지하광산의 200여개 측점에서 암반분류 측정이 이루어졌다. 이 연구의 주된 목적은 국내 석회석 광산의 최대 무지보 갱도 크기의 적정성을 검토하기 위한 것으로서 Q 시스템의 무지보 갱도폭 결정하는 관계식과 안정성 그래프법을 이용하여 관계식을 유도하고 비교검토가 이루어졌다. 또한 현장에서 기존 암반분류법 사용에 어려움을 겪고 있어 사용하기 쉽도록 GSI와 RMR을 결합한 새로운 방식의 분류법을 제안한다.

2. Q 분류법과 최대 무지보 갱도폭

2.1 Q 분류법

Q 분류법(Barton et al., 1974)은 터널 사례연구를 근거로 제안된 정량적인 분류법으로 터널지보 설계에 유용한 공학적인 암반분류체계이다. 이 분류법은 정량적인 암반평가를 위해 6개의 요소를 사용한다. 요소들은 RQD, 절리군의 수(Jn), 절리거칠기계수(Jr), 절리면의 풍화･변질계수(Ja), 지하수에 의한 저감계수(Jw) 그리고 응력저감계수(SRF)이다. 이 요소들은 3개 항으로 나누어진 곱의 형태로 표현한 것이 Q 값이며 다음 식 (1)과 같이 표현된다.

$Q=\frac{RQD}{J_n}·\frac{J_r}{J_a}·\frac{J_w}{SRF}$   (1)

Q값은 10^-3–10³(0.001-1,000) 사이의 넓은 범위의 값으로 표시되며, 계산된 Q값을 기초로 하여 암반등급을 결정하며 예외적인 불량(Exceptionally poor)에서 예외적인 양호(Exceptionally good)까지 9 등급으로 분류되어 터널폭과 Q 값에 따라 지보방법이 제시된다(Fig. 1 참조). Grimstad와 Barton(1993)은 NMT(Norwegian Method of Tunnelling)의 본질적 요소인 습식 강섬유 보강 숏크리트를 적용하기 적합하도록 본래의 38개 Q시스템의 분류범주를 Fig. 1과 같이 암반분류등급을 9개 기준으로 수정하였다. 등가굴착크기(D_e, Equivalent Dimension)는 공동의 높이나 직경 또는 폭을 터널의 용도에 의해 결정되는 굴착지보지수(ESR, Excavation Support Ratio)로 나눈 값으로 식 (2)와 같다.

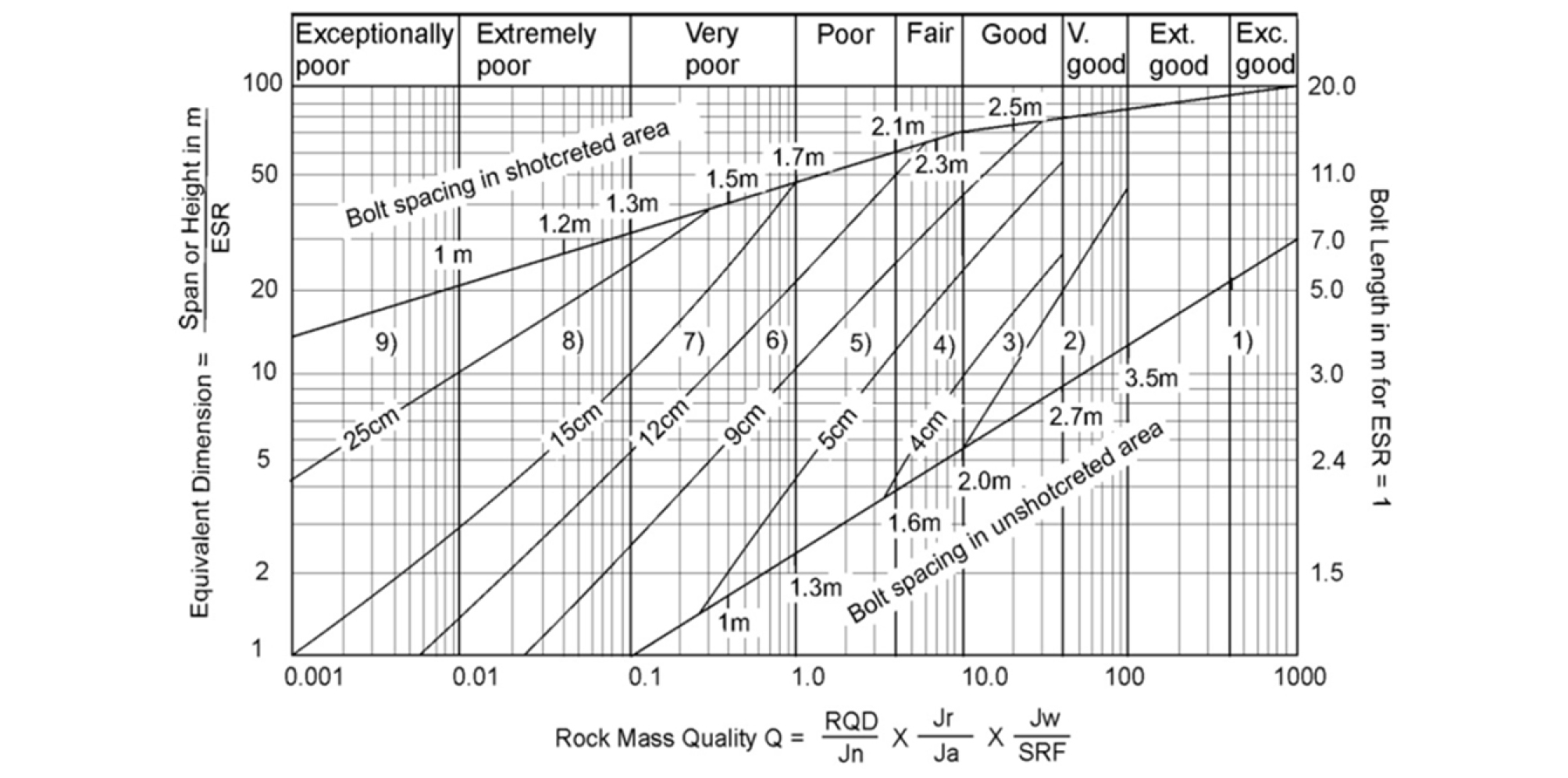
Fig. 1.

1) Unsupported, 2) Spot bolting, 3) Systematic bolting, 4) Systematic bolting, (and unreinforced shotcrete, 4 - 10 cm), 5) Fibre reinforced shotcrete and bolting, 5 - 9 cm, 6) Fibre reinforced shotcrete and bolting, 9- 12 cm, 7) Fibre reinforced shotcrete and bolting, 12 - 15 cm, 8) Fibre reinforced shotcrete, > 15 cm, reinforced ribs of shotcrete and bolting, 9) Cast concrete lining

The Q support chart (from Grimstad and Barton, 1993)

${\mathrm{D}}_{\mathrm{e}}=\frac{\mathrm{Span}orHeight\left(\mathit{m}\right)}{\mathrm{ESR}}$   (2)

여기서, 굴착지보지수(ESR)은 굴착목적과 요구되는 안정성에 따라 Table 1과 같은 값을 갖는다.

Table 1. ESR (Excavation Support Ratio values (after Barton et al., 1974)

Q값이 이용가치가 높은 것은 등가굴착크기 D_e와 Q값을 이용하여 각각의 범주에 대해 구체적인 지보대책을 제시하기 때문이다(Fig. 1). 따라서 Q 분류법은 광산 갱도에서 지보대책이나 무지보 갱도 폭의 계산 등의 적용에 있어서 RMR 분류법 보다는 경험적으로 적용범위가 넓다.

광산현장 광산기술자들이 Q시스템을 사용하기가 RMR을 사용하는 것보다 어려울 수 있기 때문에 RMR 값을 이용하여 Q 값으로 전환하는 식을 이용하는 것을 제안하고자 한다. Bieniawski(1989)에 의해 제안된 식 (3)을 이용해 RMR 값으로부터 Q값을 구할 수 있고, 국내 여러 석회석광산에서 구한 RMR 과 Q의 상관관계에서 구한 경험식 (4)를 이용할 수 있다(Sunwoo et al., 2003). 또한 국내 모든 암종에 대한 Q 값과 RMR 값과의 관계에 대한 연구에서 퇴적암에 대한 상관관계는 식 (5)와 같다(Sunwoo et al., 2001).

$RMR=9·\mathrm{In}Q+44$   (3)

$RMR=6.3·\mathrm{In}Q+45.2$    (4)

$RMR=6.07·\mathrm{In}Q+50.1$   (5)

2.2 Q 시스템을 이용한 무지보 갱도폭의 결정

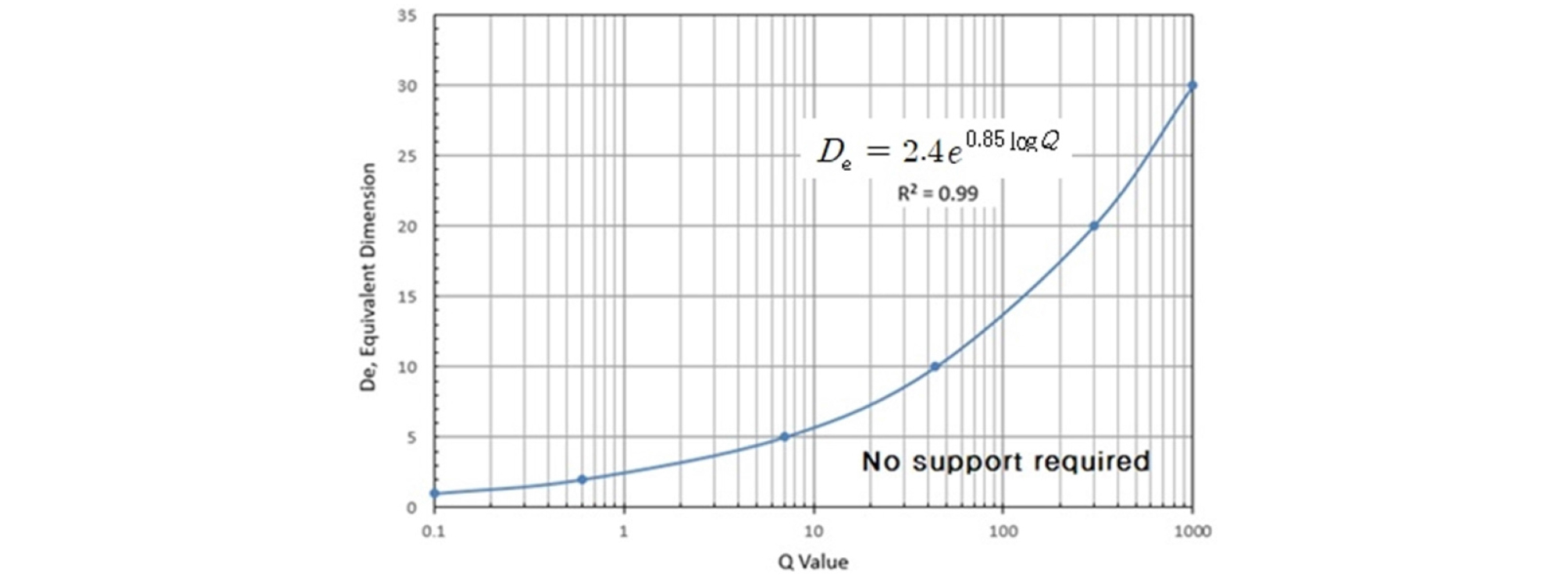
지보를 사용하지 않는 석회석광산 특성상 광산의 안정성 확보를 위해 갱도의 크기와 광주의 크기를 결정함에 있어 어려움을 겪는다. 국내에는 갱도나 광주의 크기를 결정할 수 있는 기준이 없는 상태이다. 따라서 Grimstad와 Barton(1993)이 제안한 NMT (Norwegian Method of Tunnelling)의 암반 분류등급 기준과 지보대책을 이용하여 간단하게 무지보 갱도폭을 구하는 식을 유도하여 사용할 것을 제안하고자 한다. Fig. 2는 Fig. 1의 등가굴착크기(D_e)와 Q 값의 상관관계를 도식화한 것으로 상관식은 식 (6)과 같다.

Fig. 2.

The boundary of no support required

$D_e=2.4e^{0.85\log Q}$    (6)

따라서 식 (6)을 이용하여 현장에서 구한 Q 값과 갱도의 사용목적을 고려하여 식 (7)과 같이 무지보 갱도의 최대 폭(Span_max)을 구할 수 있다.

$Spa{n}_{\max }=ESR\times D_e=ESR\times 2.4e^{0.85\log Q}$   (7)

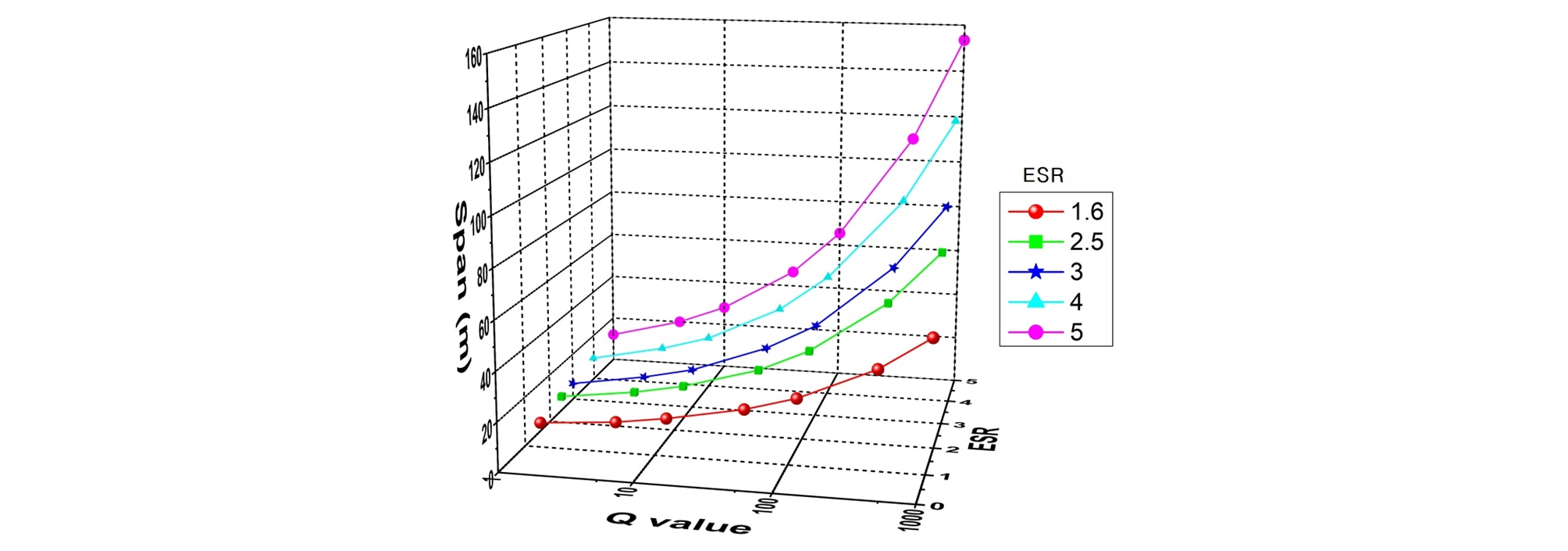
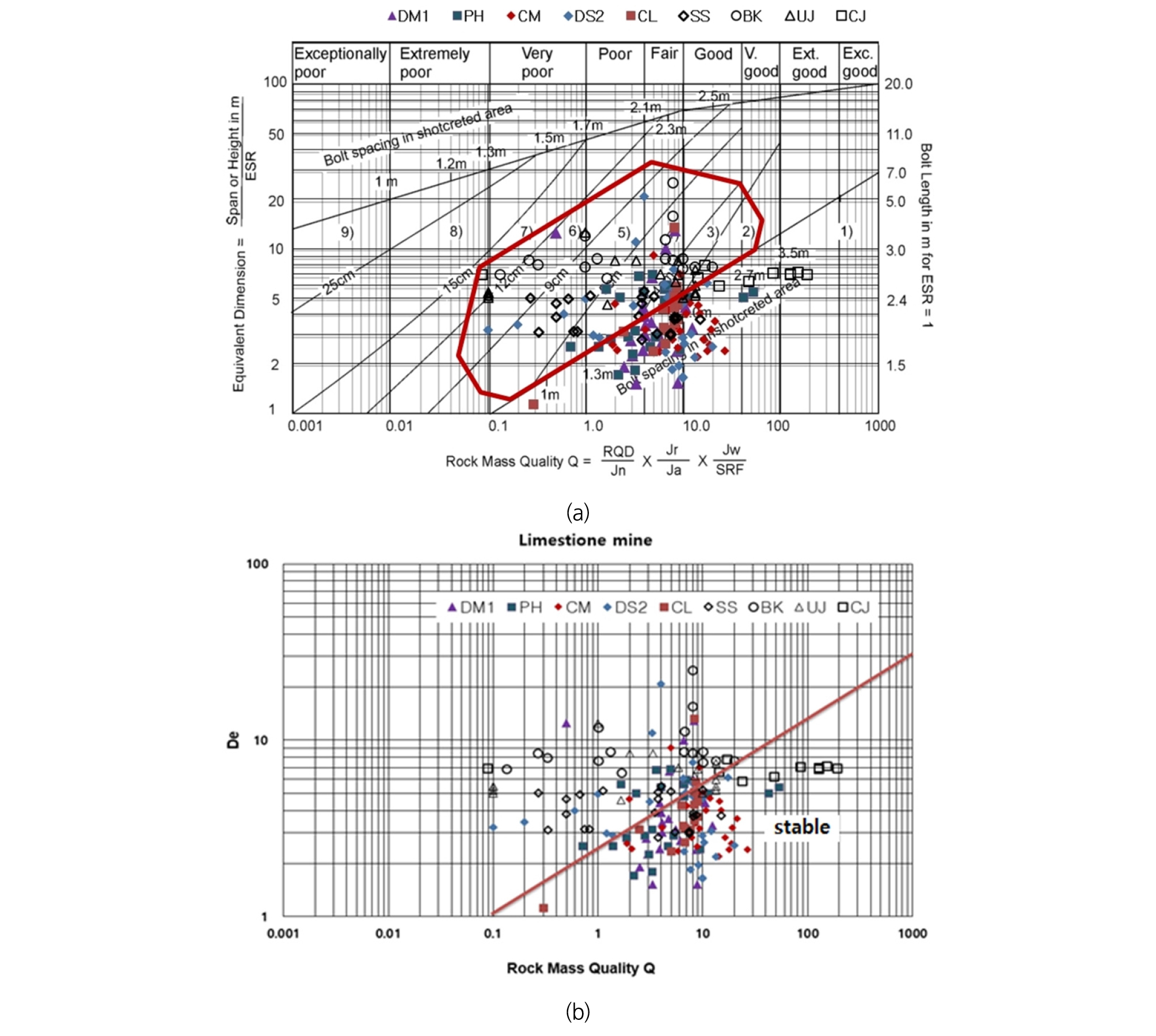
Table 2는 갱도나 공동의 사용목적별(ESR값 변화)과 Q 값의 9개 범주에 따른 갱도의 최대 무지보 규격을 나타낸 것이고, Fig. 3은 Table 2의 값을 도식화한 것이다. 국내 석회석 광산에서 무지보갱도 폭에 대한 연구를 위해 여러 지하채굴 석회석광산 200여개의 측점에서 Q 시스템을 이용한 무지보 갱도의 안전성 검토를 실시한 결과는 Fig. 4와 같다. Fig. 4(a)의 다각형 도형 안에 위치하는 점들은 모두가 지보대책이 필요한 갱도를 나타낸다. 많은 수의 갱도들은 지보형태 2)의 국부 볼팅에서 지보형태 7)의 숏크리트와 록 볼트 시공까지의 지보대책이 필요하지만(Fig. 1 참조), 대부분 광산에서는 무지보로 갱도를 유지하면서 낙석이 발생하거나 할 가능성이 있는 지역의 상황에 따라 갱도를 스케일만 실시하고 있는 실정이다. 천정이나 측벽에서 낙석이 발생하면 스케일링 정도의 조치만 취하는 경우가 대부분이다. Fig. 4(b)는 Fig. 2와 식 (6)을 이용하여 그 갱도의 최대폭을 기준으로 표시한 그래프이다.

Table 2. The span(m) of opening of no support required with variation of Q value and ESR

Fig. 3.

The span(m) of gangway of no support required with variation of Q value and ESR

Fig. 4.

The boundary of no support required

3. 안정성 그래프법과 무지보 갱도폭의 크기

3.1 안정성 그래프법(Stability graph method)

채광장에서 갱도나 공동의 안정성을 검토하기 위해서 Mathews et al.(1981)이 안정성 그래프법을 제안하였지만, 북미지역 광산의 깊은 심도의 경암 급경사 채광공동을 대상으로 한 자료들로 제한적이었기 때문에 후에 많은 학자들에 의해 자료가 추가되면서 수정보완 이루어졌다(Povin et al., 1988; Nickson, 1992; Steward & Forsyth, 1995).

이 방법은 채광공동의 안정성을 결정하기 위하여 Barton의 Q시스템을 보완하여 사용하며, Q의 첫 4개의 요소만 사용하여 Q' 값을 결정하였다. Q'는 Q값 중에서 응력저감계수(SRF)와 지하수저감계수(J_W)가 1로 간주된 값으로 식 (8)과 같다.

$Q^{\text{'}}=\frac{RQD}{J_n}·\frac{J_r}{J_a}$   (8)

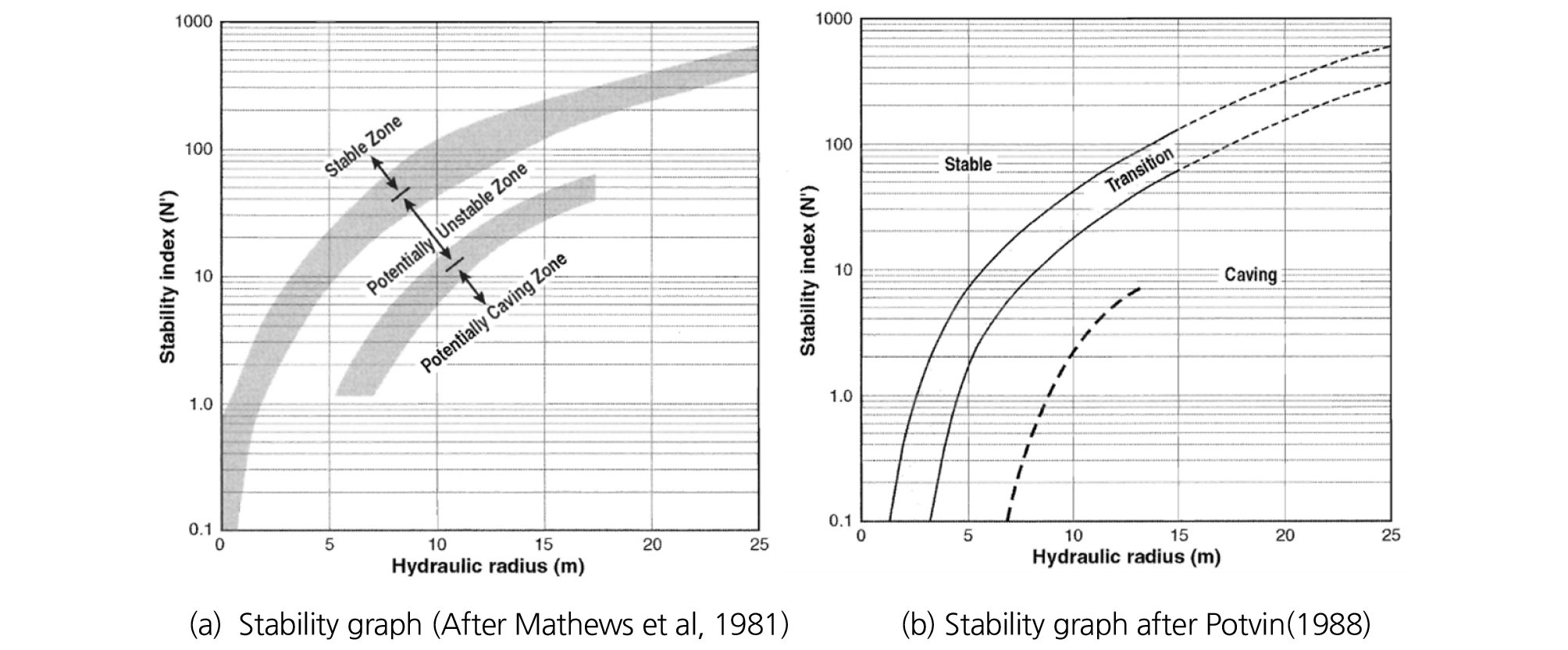
안정성 그래프법은 수리반경 (Hydraulic radius) 또는 형상계수 (Shape factor) (식 (9) 참조) 그리고 안정성 계수 N(식 (10) 참조)으로 도식화된다. 초기에는 Fig. 5(a)와 같이 안정지역 (Stable zone), 잠재적 불안정지역 (Potentially unstable zone), 잠재적 붕락지역 (Potentially caving zone)으로 구분하였다. 그러나 Potvin et al.(1988)은 보다 많은 자료를 수집함으로써 안정성 그래프법의 평점 보정요소들을 재정의하여 수정 안정성 그래프법을 제안하였고, Fig. 5(b)와 같이 좁은 폭의 전이지역, 안정 및 붕락지역으로 구분하였다.

Fig. 5.

The stability graphs

수리반경(HR) 혹은 형상계수(S)는 안정성 평가를 위해 객관적이며 보다 정확성을 높이기 위해 공동 또는 갱도의 모양과 크기의 영향을 도입한 것으로 공동 단면적 에 대한 공동 둘레의 비로 정의되며 식 (9)와 같다.

$HRorS=\frac{W·H}{2\left(W+H\right)}$   (9)

여기서, W는 공동 또는 갱도의 폭, H는 높이.

안정성 계수(Stability number) N은 다음 식 (10)과 같다

$N=Q^{\text{'}}\times A\times B\times C$   (10)

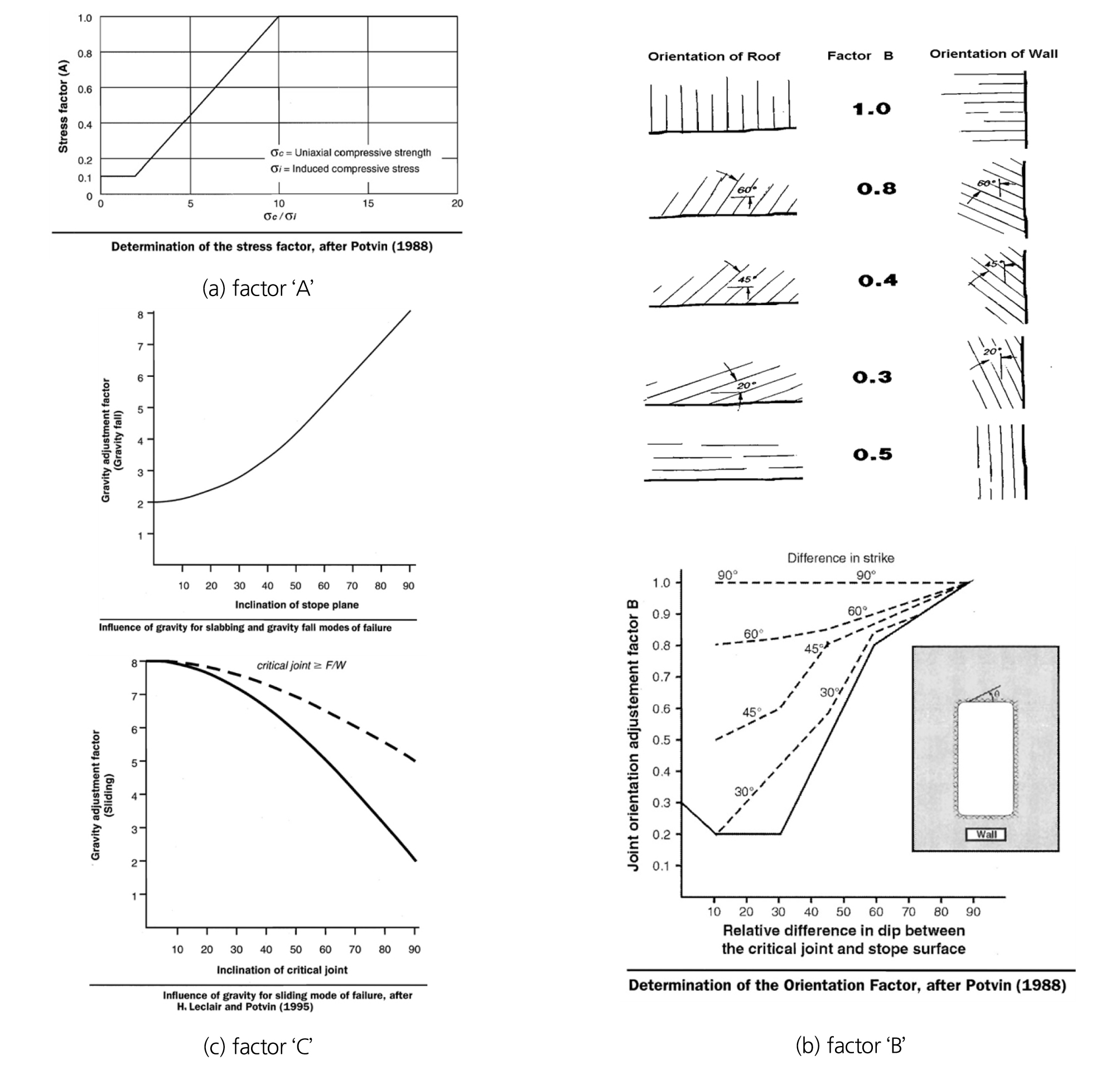
여기서, 요소 A는 응력계수(Stress factor)로서 암반의 안정성을 감소시키는 높은 응력의 영향을 고려하는 것이다(Fig. 6(a)). 이 값은 무결암의 일축압축강도 값을 공동표면에 평행하게 유도되는 최대 유도응력치로 나눈 값으로 정의된다.

Fig. 6.

Adjustment factors for determination of stability number (After Mathews et al, 1981)

요소 B는 절리방향보정계수(Joint orientation factor)를 나타내며 공동표면과 가장 위험한 불연속면의 방향성이 미치는 영향에 관한 것이다(Fig. 6(b)). 대상 공동표면 에 90°인 불연속면은 안정성에 문제가 되지 않기 때문에 1의 값이 주어진다. 공동표면에 대해 20° 이내의 경사를 가지는 불연속면은 공동내에서 전도될 수 있기 때문에 안정성을 감소시키는 높은 응력의 영향을 고려하는 것이다.

요소 C는 낙석 및 박리파괴 (slabbing) 또는 미끄럼 파괴에 대한 중력의 영향 즉 파괴와 공동표면의 방향과 관련된다. 공동의 수직벽에는 8의 값과 수평의 천정에 대해서는 2의 값이 주어진다(Fig. 6(c)). 이 계수는 근본적으로 수평의 천정에 비해 수직벽이 더 안정하다는 것을 반영한다.

3.2 안정성 그래프법을 이용한 최대 무지보 갱도크기 결정

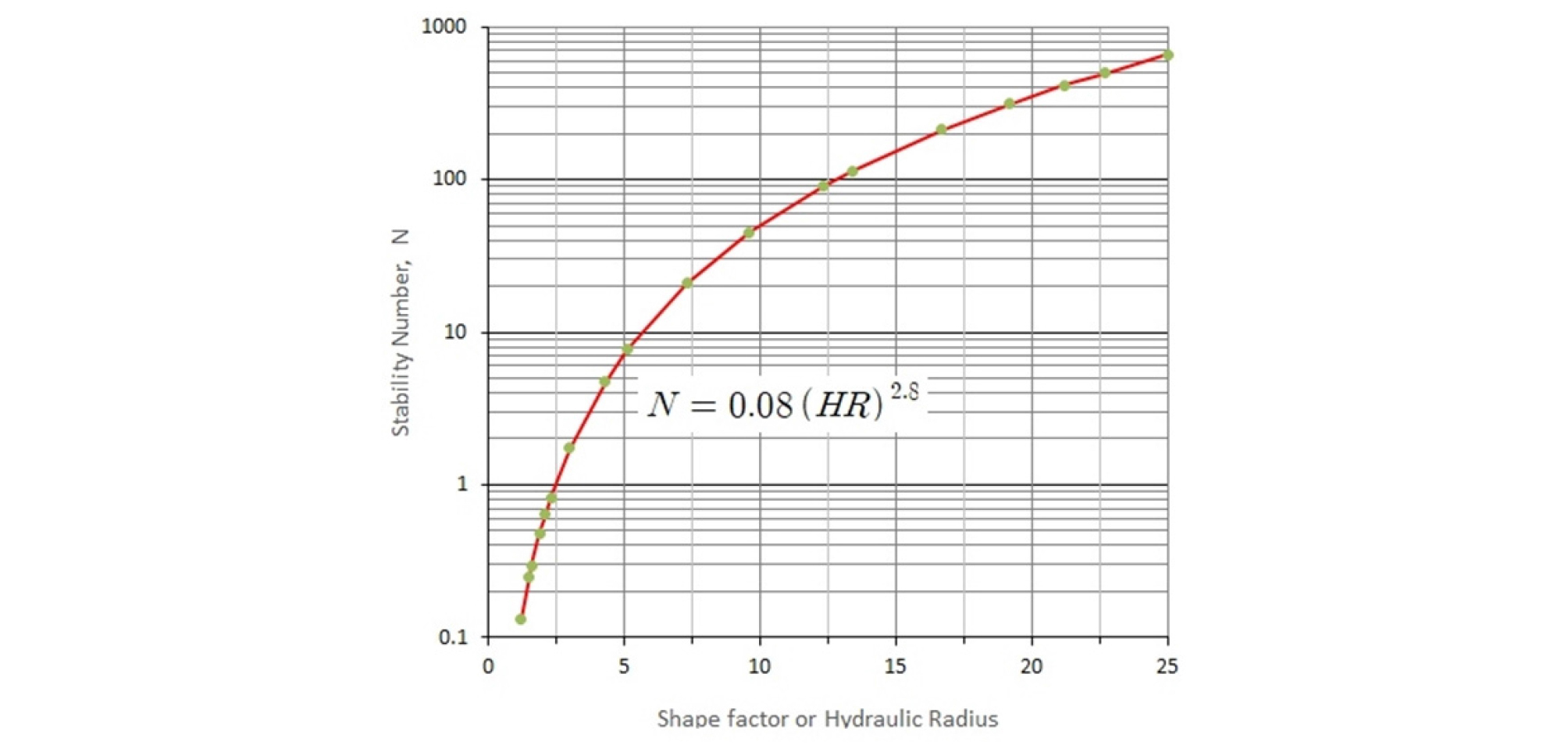
안정성 그래프법에서 제안된 수리반경과 안정성 계수를 이용한 안정성 판단의 근거가 되는 한계곡선을 수식화하여 사용하고자 한다(Fig. 7). 안정성계수 N과 수리반경 HR의 상관 관계식은 식 (11)과 같이 구해진다.

Fig. 7.

The boundary of no support required

$N=0.08H{R}^{2.8}$   (11)

따라서 현장에서 구한 N 값을 적용하여 그 갱도의 높이(H)와 폭(W)를 알고 있기 때문에 식 (11)을 이용하여 안정성을 판단함으로써 적용 갱도폭의 최대값을 최대 무지보 갱도폭으로 사용할 수 있다.

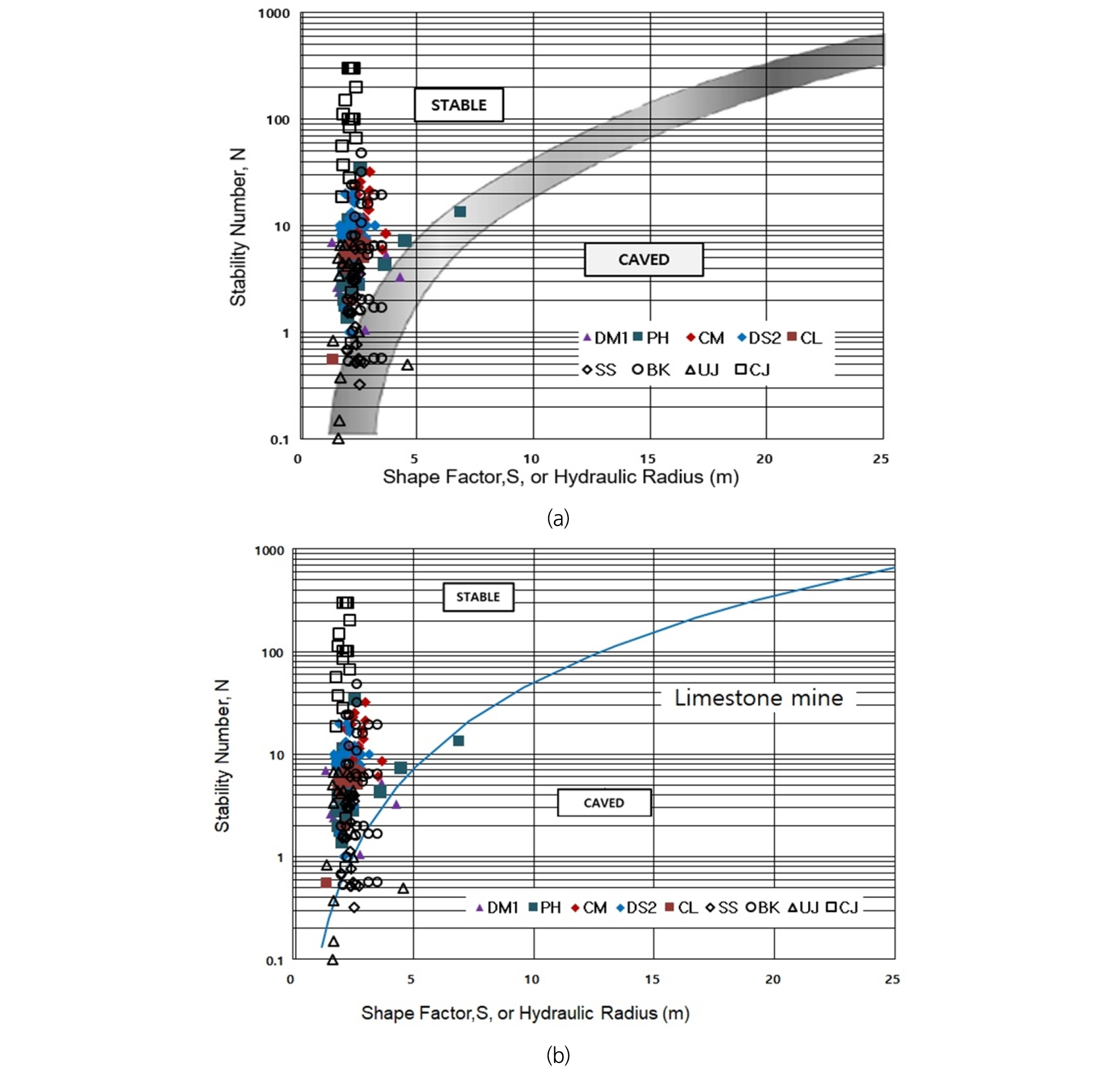
앞에서 언급한 200 여개 측점의 자료를 안정성 그래프법을 이용하여 안정성에 대한 검토가 이루어졌으며 그 결과는 Fig. 8과 같다. 좌상단의 점들은 모두 지보가 필요 없는 안전한 갱도들이다. 그림내 경계선 내의 부분적 불안정 지역을 제외하면 붕락가능 지역은 한 곳으로 나타나고 있다(Fig. 8(a)). 그러나 현장에서 사용하게 쉽게 단순화시키기 위해 수식을 이용한 한 경계선만을 사용하여 부분적으로 불안정한 지역을 위험지역으로 간주하게 하여 안정성을 판단하게 한다 (Fig. 8(b)). Fig. 4와 비교하여 상당한 차이를 볼 수 있다. 이 차이는 대부분 광산현장에서의 조사는 붕괴가 된 곳이나 위험 가능성이 큰 곳에서는 조사를 할 수 없기 때문에 갱도가 안정하다고 판단되는 접근가능한 곳에서 이루어진다. 따라서 안정하다고 판단되는 갱도에서 측정하기 때문에 Q의 무지보 범위에 속하는 측점인 갱도의 안전성과과 그래프법의 붕락에 속하는 안정된 개소의 차이가 나는 이유가 된다.

Fig. 8.

The boundary of no support required

4. 새로운 암반분류법의 제안

새로운 암반분류법의 제안 이유는 광산현장의 기술인력 부족으로 실제로 암반평가를 실시할 수 있는 광산이 별로 없으므로. 암반분류법중에서 사용이 다소 용이한 GSI 분류법을 이용하여 RMR법의 2개 요소를 결합하여 현장에서 쉽게 사용할 수 있는 분류법을 제안하고자 하는 것이다. Hoek(1994), Hoek and Brown(1997)에 의해 제안된 정성적인 방법인 GSI(Geological Strength Index)는 현지암반의 강도와 Hoek-Brown 상수뿐만 아니라 절리암반의 탄성계수와 같은 암반의 역학적 성질을 추정할 수 있는 시스템을 제공하는 것이다. GSI는 현장에서 육안관측으로 사용할 수 있는 실용적인 시스템으로 크게 암반의 강도를 추정할 수 있는 암반의 구조적인 형태와 절리의 거칠기와 변형정도로 표시되는 불연속면의 표면적인 조건의 두 가지 요소로 구성된다.

가장 많이 사용되고 있는 RMR의 경우 조사나 시공단계에서 암반평가를 위한 실제 조사에서도 RQD 값을 구하기위한 시추공의 시추작업이 제한될 뿐만 아니라 시공시에는 시추공을 위한 시추작업이 전혀 이루어지지 않는 실정이다. 따라서 RQD요소를 보다 간단히 측정할 수 있고 또한 절리간격과 같은 요소도 실제로는 RQD와 중복되는 요소로서 간편하게 시추공의 코아에 의존하지 않고 암반평가를 실시할 수 있는 암반분류법을 개발하는 것이 목적이다.

이것은 GSI를 구성하는 요소가 암반의 구조적인 형태와 절리의 거칠기와 변형정도로 표시되는 불연속면의 표면적인 조건으로 구성되기 때문에 결국은 RMR의 불연속면과 관련된 RQD, 불연속면의 간격요소들은 GSI의 암반의 구조요소와 유사하다. 또한 GSI에서는 암석의 강도문제나 지하수 문제 등이 고려되지 않고 있다. 따라서 GSI의 관찰의 용이함을 이용하고 RMR의 상기 두 요소를 합쳐 새로운 암반 분류법을 제안하고자 한다. 먼저 현장에서 관측이 쉬운 GSI의 암반구조 부분을 RMR 분류법에 적용하는 방법으로 RMR의 요소 중 RQD요소(20점) + 간격요소(SP, 20점) 불연속면의 조건(COD, 30점)의 합계점수 70점에 대해 현장에서 측정한 GSI의 값을 70점 만점으로 환산한 값을 GSI₇₀이라 표시한다(식 (12) 참조). 그리고 GSI₇₀에서 구한 값에 RMR 요소중 암석의 강도(UCS, 15점)와 지하수 요소(GW, 15점)의 두 요소를 합쳐 새로운 암반분류법(KGR(Korean GSI and RMR)이라 칭함)의 평점으로 한다(식 (13)).

$GS{I}_{70}=GSI/100\times 70$   (12)

$KGR=GS{I}_{70}+UCS+GW$    (13)

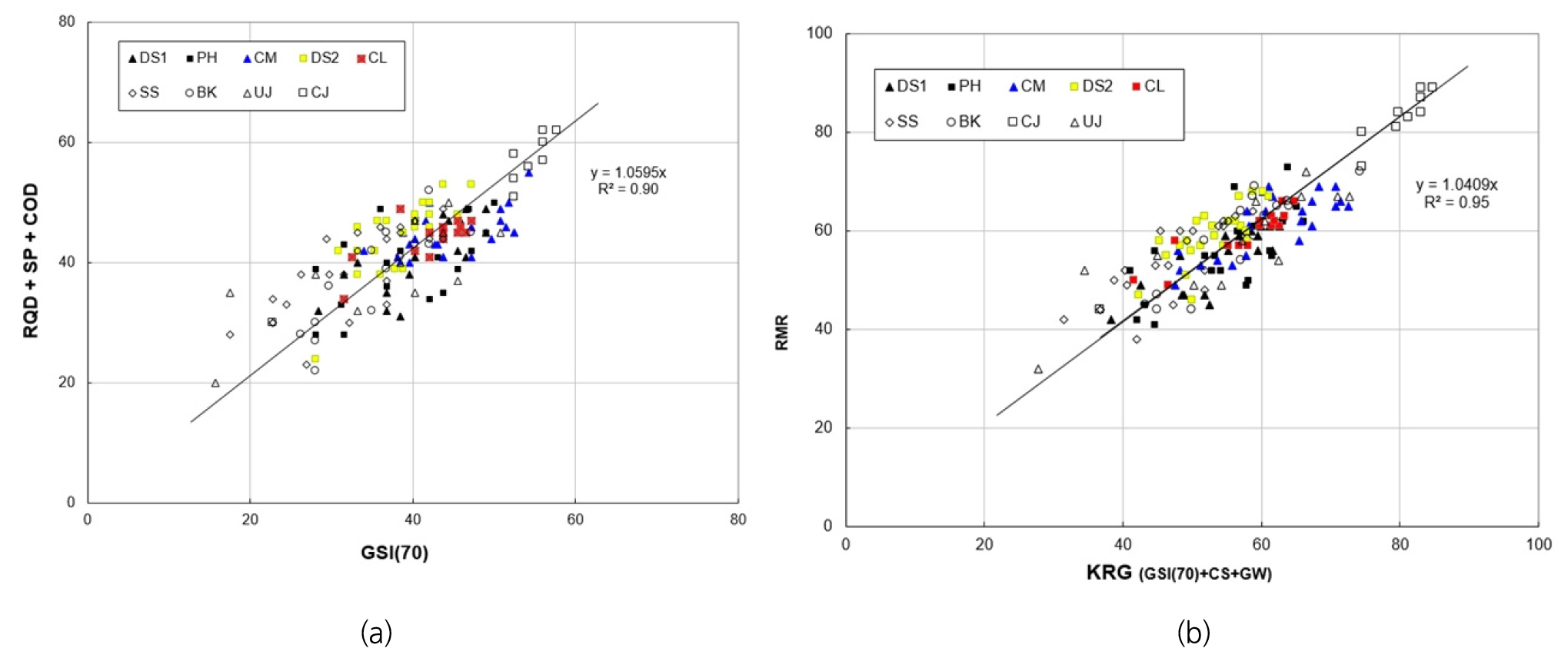
Fig. 9(a)는 현장에서 측정한 GSI의 값을 70점 만점으로 환산한 값(GSI₇₀)에 대한 RMR의 지하수요소(GW)와 압축강도요소(UCS)를 제외한 값 즉 불연속면 특성과 관련된 요소 값(지하수조건, RQD, 간격요소)과의 상관관계를 표시한 것이고, 두 상관관계의 기울기가 1.06으로 거의 1에 근접하고 상관관계()도 상당히 양호하다. Fig. 9(b)는 현장에서 측정한 RMR과 KGR 값(식 (13) 참조)과의 상관관계를 표시한 것으로 두 상관관계의 기울기가 1.04로 거의 1에 근접하고 상관관계()도 상당히 양호하다. 따라서 RMR 값 대신에 KRG 값을 RMR 값으로 대체해도 무난하다고 생각된다. 따라서 암반평가를 위해 필요한 요소는 RMR의 요소 중 압축강도와 지하수요소만을 평가하고 GSI 도표를 작성함으로써 기존의 RMR 보다는 쉽게 현장에서 암반평가를 실시할 수 있을 것으로 예상한다.

Fig. 9.

The relationship of KRG

5. 결 과

지하광산에서 갱도나 공동의 안정성은 생산성과 안정을 확보해야 하는 광산운영상 갱도나 채굴적 공동의 폭은 하나의 중요한 설계요소가 된다. 그러나 국내에는 이에 대한 기준이 없기 때문에 현장에서 쉽게 사용하기 위해서 암반분류법 중에 Q 시스템을 이용하여 국내 석회석 광산에서 무지보로 유지할 수 있는 최대 무지보 갱도 폭을 결정하는 관계식과 안정성 그래프를 이용한 최대 무지보 갱도 폭을 결정하기 위한 검토가 이루어졌다. 또한 현장에서 암반분류를 보다 용이하게 사용할 수 있도록 GSI와 RMR을 결합한 새로운 방식의 분류법을 제안한다.

등가굴착크기(D_e)와 Q 값의 상관관계를 이용하여 현장에서 구한 Q 값과 갱도목적을 고려한 식 (7)을 이용하여 무지보 갱도의 최대 폭(Span_max)을 구할 수 있다. 또한 갱도나 공동의 목적별(ESR값 변화)과 Q 값의 9개 범주에 따른 갱도의 최대 무지보 규격을 나타내는 표(Table 2)도 제시하였다.

안정성 그래프법에서 제안된 수리반경과 안정성 계수를 이용한 안정성 판단의 근거가 되는 한계곡선을 수식화하여 최대무지보 갱도폭의 결정에 사용했다. 현장에서 구한 N 값을 적용하여 그 갱도의 높이(H)와 폭(W)를 알고 있기 때문에 식 (11)을 이용하여 안정성을 판단함으로써 적용 갱도폭의 최대값을 최대 무지보 갱도폭으로 사용할 수 있다.

또한 현장에서 사용하기 쉽도록 새로운 GSI와 RMR을 결합한 새로운 방식의 암반분류법 KGR을 제안했다. 현장에서 측정한 GSI의 값을 70점 만점으로 환산한 값(GSI₇₀)에 RMR의 지하수요소와 압축강도요소를 합한 값을 사용한다. 따라서 암반평가를 위해 RMR의 요소중 압축강도와 지하수요소만을 평가하고 GSI 도표를 작성함으로써 기존의 RMR 보다 쉽게 현장에서 실시할 수 있을 것으로 예상한다.

대부분 광산현장에서의 조사는 갱도가 개설이 되고 난 후 갱도가 유지되고 있는 곳에서 이루어진다. 붕괴가 된 곳이나 위험 가능성이 큰 곳에서는 조사를 할 수 없기 때문에 갱도가 안정하다고 판단되는 접근가능한 곳에서 이루어진다. 따라서 안정하다고 판단되는 갱도에서의 측정 때문에 Q의 무지보 범위에 속하는 측점인 갱도의 안전성과 그래프법의 붕락에 속하는 안정된 개소의 차이가 나는 이유가 된다고 본다. Q의 무지보 범위에서는 지보가 필요한 갱도가 다소 위험이 있는 지역일지라도 스케일 등으로 위험이 관리가 되고 있는 갱도들로 판단하면 된다. 그러므로 보다 더 정확한 자료의 획득을 위해서는 갱도 개설당시부터 안정성 검토가 이루어지는 것이 좋고, 그리고 갱도가 개설된 후 일정시간이 경과된 후에 정기적으로 안정성 검토를 통한 붕락 및 위험여부를 판단하는 것이 바람직하다고 본다.