1. 서 론
2. 지반조사 및 현장시험
2.1 지반조사
2.2 그라운드 앵커 시공
2.3 현장시험
3. 수치해석
3.1 지진파 선정
3.2 모델링
3.3 물성치
4. 결 과
4.1 반력판의 침하
4.2 정착부 수직변위
4.3 정착부 수평변위
4.4 정착부 축력
5. 결 론
1. 서 론
2016년과 2017년 경주와 포항에서 발생한 강도 5.8, 5.4의 지진으로 우리나라도 더 이상 지진으로부터 안전지대가 아님을 확인하였다. 이후 내진설계 기준에 관한 연구가 지속적으로 수행되어지고 있으며, 구조물 설계시 지진에 대한 고려를 필히 수행하게 되어 있는 실정이다. 앞서 언급된 포항에서 발생한 지진은 경주에서 발생한 지진에 비해 규모가 0.4만큼 작아 에너지 기준 3.98배 더 작은 지진임에도 불구하고 그 피해액은 경주에 비해 3배 더 크게 발생하였다. 이러한 원인은 경주와 포항의 지반특성에 따른 영향도 있지만, 많은 연구자들은 지진의 주기특성이 상부구조물에 미치는 영향을 그 원인으로 지적하였다. Lee and Oh(2017)에 따르면, 지진은 주기특성에 따라 장주기와 단주기로 구분할 수 있는데 경주와 포항 지진 모두 단주기에 속한다. 하지만 포항에서 발생한 지진이 경주지진에 비해 그 주기가 더 짧고, 그로 인해 낮은 건물들에 큰 영향을 미친 것으로 판단된다. 하지만, 현재 국내에서 사용하고 있는 내진설계의 기준은 미국 서부 기준의 장주기 특성을 가지고 있는 지진주파수를 사용하고 있으며, 이를 개선하기 위한 노력의 필요성이 대두되고 있는 실정이다. 이렇게 지진은 우리가 사용하고 있는 구조물의 안정성에 직접적으로 영향을 미치고 있다. 하지만 대부분의 지진에 관한 연구는 주로 터널 및 상부 건물과의 상호거동에 관한 연구가 이루어지고 있는 실정이다(Amorosi and Boldini, 2009; George and Dimitri, 2010; Koseki et al., 2012; Yu et al., 2013; Lee et al., 2016; Ha et al., 2017; You and Kim, 2018). 터널 및 상부구조물은 Soil nail, rock bolt, geogrid, ground anchor등과 같은 다양한 보강재로 구조적 안정성을 확보하고 있다. 그 중 ground anchor는 가장 널리 사용되고 있는 보강공법 중 하나로써 많은 구조물의 안정성을 확보하기 위해 사용되고 있다. 특히, 비탈면, 옹벽, 기초구조물 등에 토압 또는 부력에 대한 구조적 안정성을 확보하기 위해 많이 사용되고 있다. 이러한 보강재의 안정성은 사용구조물의 안정성과 직결되지만, 보강길이 및 수량 등을 산정할 때 단순한 수식을 통해 설계를 수행하고 있어, 지진의 영향에 대한 연구가 필요한 실정이다. 따라서, 본 연구에서는 실제 현장에서 그라운드 앵커의 인장시험을 수행하고, 수치해석을 통해 지진하중을 고려하여 그라운드 앵커의 축력을 변화를 분석하였다. 지진하중은 주기특성을 고려하여 장주기와 단주기로 구분하여 적용하여 주기 특성에 따른 그라운드 앵커의 거동 특성을 분석하였다.
2. 지반조사 및 현장시험
2.1 지반조사
현장시험은 동양대학교에서 수행되었다. 현장시험을 위한 그라운드 앵커를 시공하기 전에 앵커의 정착길이와 설계력을 산정하기 위해 지반조사를 수행하였다. 지반조사 결과 풍화토가 약 7.0 m두께로 나타났고, 하부는 풍화암이 존재하는 것으로 나타났다. 풍화토와 풍화암의 대표 N치는 각각 30회/30cm, 50회/10cm로 파악되었다. 지반조사로부터 얻은 깊이에 따른 N치를 Fig. 1에 나타내었다.
2.2 그라운드 앵커 시공
지반조사를 통해 추정한 지반의 물성치를 이용하여 그라운드 앵커의 정착길이를 산정하였다. 풍화암에 정착하는 것을 목표로 자유장은 약 7.0 m로 산정하였으며, 정착장은 설계하중 400 kN을 목표로 4.0 m로 산정하였다. 천공직경은 105 mm로 산정되었으며, 정착길이는 그라운드 앵커 설계・시공 유지관리 매뉴얼(Ministry of Land, 2009)을 참조하여 천공직경, 정착길이, 그라우트-지반 주면마찰력, 강연선-그라우트 마찰력을 고려하여 산정하였다 (식 (1)). Equation (1)에서 알 수 있듯이, Lbf, Lbs는 지반-그라우트의 마찰정착장과 강연선-그라우트의 마찰정착장을 각각 의미한다. 식 (2), (3)는 각각의 마찰정착장을 산정하는 식이다.
| $$L_b=MAX(L_{bf},\;L_{bs})$$ | (1) |
| $$L_{bf}=\frac{T_{Design}\times F.S}{\mathrm\pi\times D\times\tau_f}$$ | (2) |
| $$L_{bs}=\frac{T_{Design}}{U\times\tau_a}$$ | (3) |
여기서, TDesign : Anchor Design load
F.S : Factor of safety
D : Diameter of bore hole
τf : Ultimate shaft friction resistance stress (grount-ground)
τa : Ultimate shaft friction resistance stress (PC strand-grout)
U : Circumference of PC strand
그라운드 앵커의 형식은 마찰인장형으로 선정하였으며, 시공 과정을 Fig. 2에 나타내었다.
2.3 현장시험
본 연구는 실제 현장에서 사용되는 그라운드 앵커에 긴장력을 도입한 후 지진하중 적용에 따른 지반 및 앵커 정착장의 거동 특성을 분석하는데 그 목적이 있다. 따라서, 현장시험의 과정을 수치해석에서 동일하게 모사한 후, 지진파를 입력하였다.
그라운드 앵커의 현장시험은 크게 3가지로 구분할 수 있는데, ① 극한인발시험, ② 인장시험, ③ 확인시험으로 구분할 수 있다. 극한인발시험은 실제 보강이 필요한 현장에 앵커를 시공하기 전 앵커의 설계인장력을 산정하기 위해 지반의 주면마찰저항을 측정하는데 그 목적이 있다. 따라서, 극한인발시험은 그라운드의 정착부가 설치될 지반까지 천공한 후 앵커체를 삽입하고 그라우트를 양생하여 긴장력을 도입한다. 극한인발시험에서 주의할 점은 이 시험의 목적이 지반의 주면마찰저항을 산정하는 것이므로 강연선의 파단이 발생하지 않고 그라우트-지반의 경계면에서 파괴가 발생하여 앵커체의 인발이 이루어져야 한다. 따라서, 설계예정인 앵커체의 길이, 천공경, 강연선 수 등에는 큰 의미가 없으며, 강연선이 파단되지 않은 상태에서 앵커가 인발되는 시점에서의 하중 측정 후, 시공된 앵커체의 직경 및 길이로 역산하여 지반의 주면마찰저항을 산정한다. 인장시험은 극한인발시험을 통해 산정된 앵커의 설계인장력이 합리적으로 산정되었는지를 판단하는 시험이다. 따라서, 지반의 소성변위를 측정하는 것이 중요하며, 이를 위해 긴장력의 재하/제하 과정을 반복하며 앵커의 변위를 측정하여 탄성변위와 소성변위를 구분하여 설계앵커력을 조절한다. 이를 위해 시험에 사용되는 앵커체는 실제 현장에 적용될 앵커체의 규격과 동일해야 한다.
확인시험은 실제 현장에서 앵커의 보강력을 확보하는 단계이다. 확인시험은 설계앵커력을 약 4~5단계로 구분하여 긴장력을 도입하여 수행된다. 확인시험을 통해 긴장력이 도입된 앵커의 시공상태 여부를 확인할 수 있는 방법은 크게 2가지로 구분할 수 있다. 첫 번째는 앵커 시공 시 정착구에 load cell을 설치하여 이를 통해 앵커에 작용하는 하중을 측정하는 방법과 두 번째는 긴장력 도입에 따른 단계별 늘음량을 측정하여 앵커 형식에 따른 늘음량 상한선 및 하한선 기준에 부합 여부를 판단하는 방법이다. 늘음량의 상한선 하한선 기준은 Geotechnical Control Office (1997)의 기준이 가장 널리 사용되고 있으며, 본 연구에서 사용된 마찰인장형 앵커의 확인시험시 늘음량 상한선, 하한선 기준을 식 (4)에 나타내었으며, 본 연구에서는 첫 번째 방법인 하중계를 설치하여 앵커에 작용하는 하중을 측정하였다.
| $$\frac{P_J\;\times\;0.9L_f}{E_s\times A_s}\leq\bigtriangleup l_j\leq\frac{P_J\;\times\left(L_f+0.5\times L_b\right)}{E_s\times A_s}$$ | (4) |
여기서, PJ는 도입된 긴장력을 의미하며, Lf, Lb는 자유장 및 정착장, Es, As는 강연선의 탄성계수 및 단면적을 의미하며 △lj는 긴장력 도입에 의해 발생된 강연선의 늘음량을 의미한다. 이 식에서 알 수 있듯이, 마찰인장형의 경우 시공오차로 인해 자유장이 설계값에 비해 10% 가량 짧게 시공되는 것과 강연선에 도입된 긴장력으로 인해 그라우트에 인장응력이 발생하고 그로인한 인장균열이 진행되어 정착부의 50%가 손실되는 경우까지 고려되어 앵커의 기능을 감안하는 것을 알 수 있다.
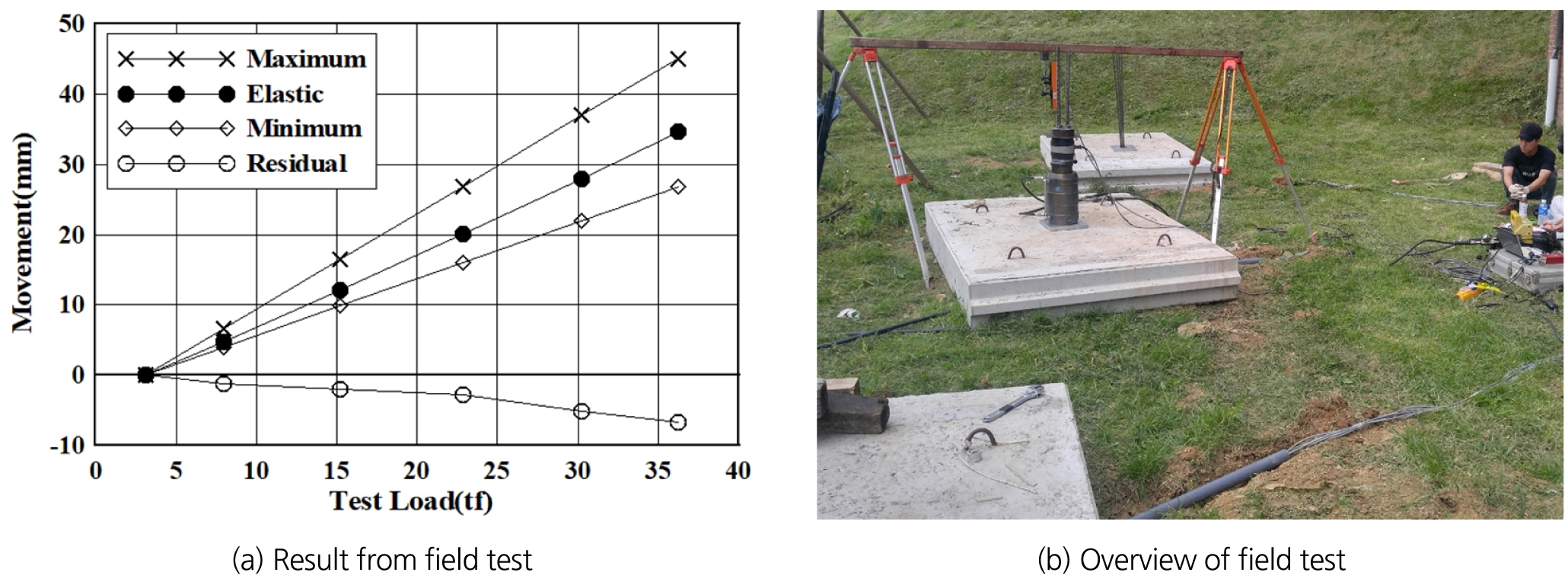
본 연구에서는 극한인발시험은 수행되지 않았으며, 인장시험 수행 후 확인시험을 통해 현장시험이 이루어졌다. 인장시험을 통해 당초 계획되었던 설계앵커력 400 kN을 350 kN으로 수정하였다. 이는 부족한 지반조사로 인해 지반 물성치 산정에 오차가 원인인 것으로 판단되며, 인장시험 결과를 및 전경을 Fig. 3에 나타내었다.
3. 수치해석
3.1 지진파 선정
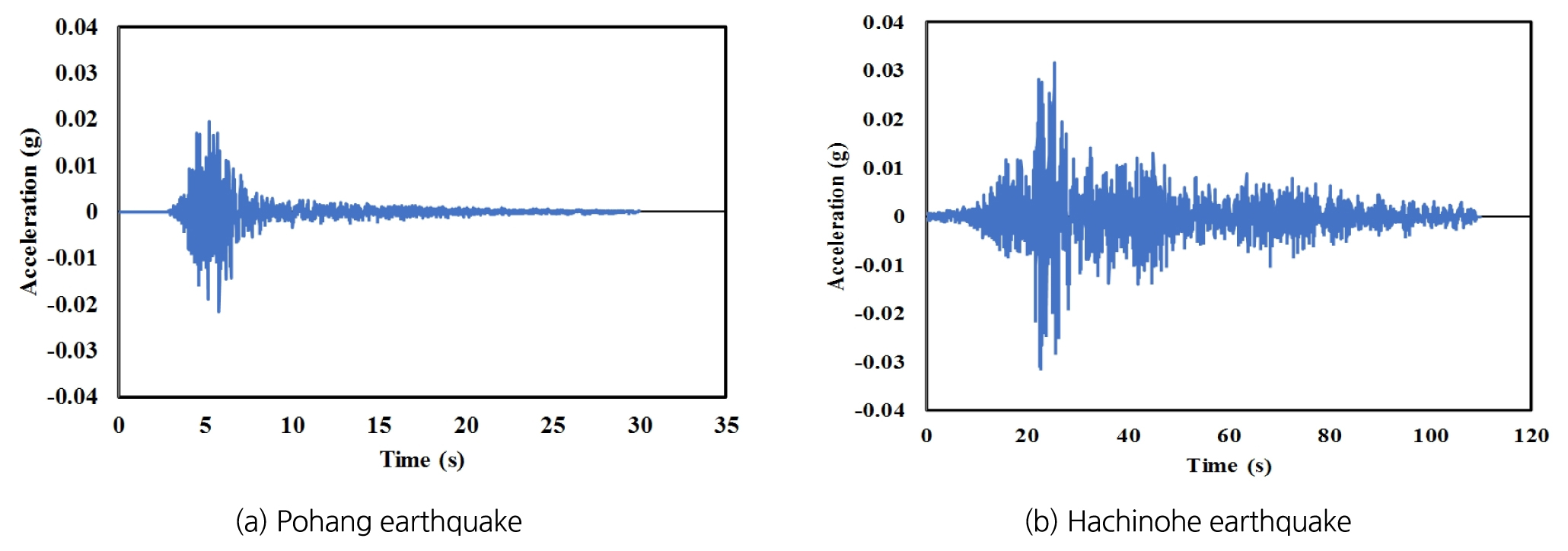
수치해석에 지진하중을 입력하기 위해 지진파를 산정하였다. 지진파는 장주기 지진(Hachinohe), 단주기 지진(Pohang, 2017)을 산정하였다. 지진파 가속도는 재현주기 1000년 기준 0.154 g를 기본으로 하였다 (Fig. 4). 이 중 포항지진은 단주기 지진의 특성을 대표한다고 할 수는 없으나, 국내에 발생하여 큰 피해를 입힌 지진 중 가장 최근에 발생하여 적용하였다.
3.2 모델링
유한요소(차분)해석에서 지진하중을 고려할 경우, 경계조건, 요소크기 등의 결정은 정적해석과 달리하여야 한다. 경계조건의 경우 기반암으로부터 전달되는 지진파가 대상구간의 경계에서 반사되지 않도록 하여야 한다. 이를 위해 측면 경계에서는 damper를 모사한 조건을 설정해야하며, 본 연구에서 사용된 Plaxis (2018)의 경우 Free-field 조건이다. 하부 경계조건 또한, 기반암으로부터 전달되는 지진파가 반사되어 지반의 동적거동에 영향을 미치는 것을 방지하여야 하며, 이를 위해 지진파를 디콘볼루션(deconvolution)하여 하부 경계조건을 rigid로 설정하는 방법과 deconvolution하지 않고 damper를 설치한 경계조건을 설정할 수 있다. Park et al. (2010)에 따르면, 앞서 말한 두 가지 방법에 따른 지반의 동적거동 특성은 크게 차이가 없는 것으로 나타났다. 따라서, 본 연구에서는 지진파를 deconvolution 하지 않고 하부 경계조건을 compliant base로 설정하여 감쇠효과를 고려하였다.
요소의 크기 또한 지진파에 의한 지반의 거동에 영향을 미치는 것으로 알려져 있다. Song et al. (2008)에 따르면, 요소의 직경을 D로 설정했을 경우, 이 요소가 전파할 수 있는 최대 주파수는 로 요소의 크기가 과도하게 크면 fmax이상의 주파수를 모두 필터링하게 되어 해석 결과가 과소하게 나타날 수 있다. 따라서, 본 연구에서는 요소의 직경이 1 m가 되도록 산정하였다.
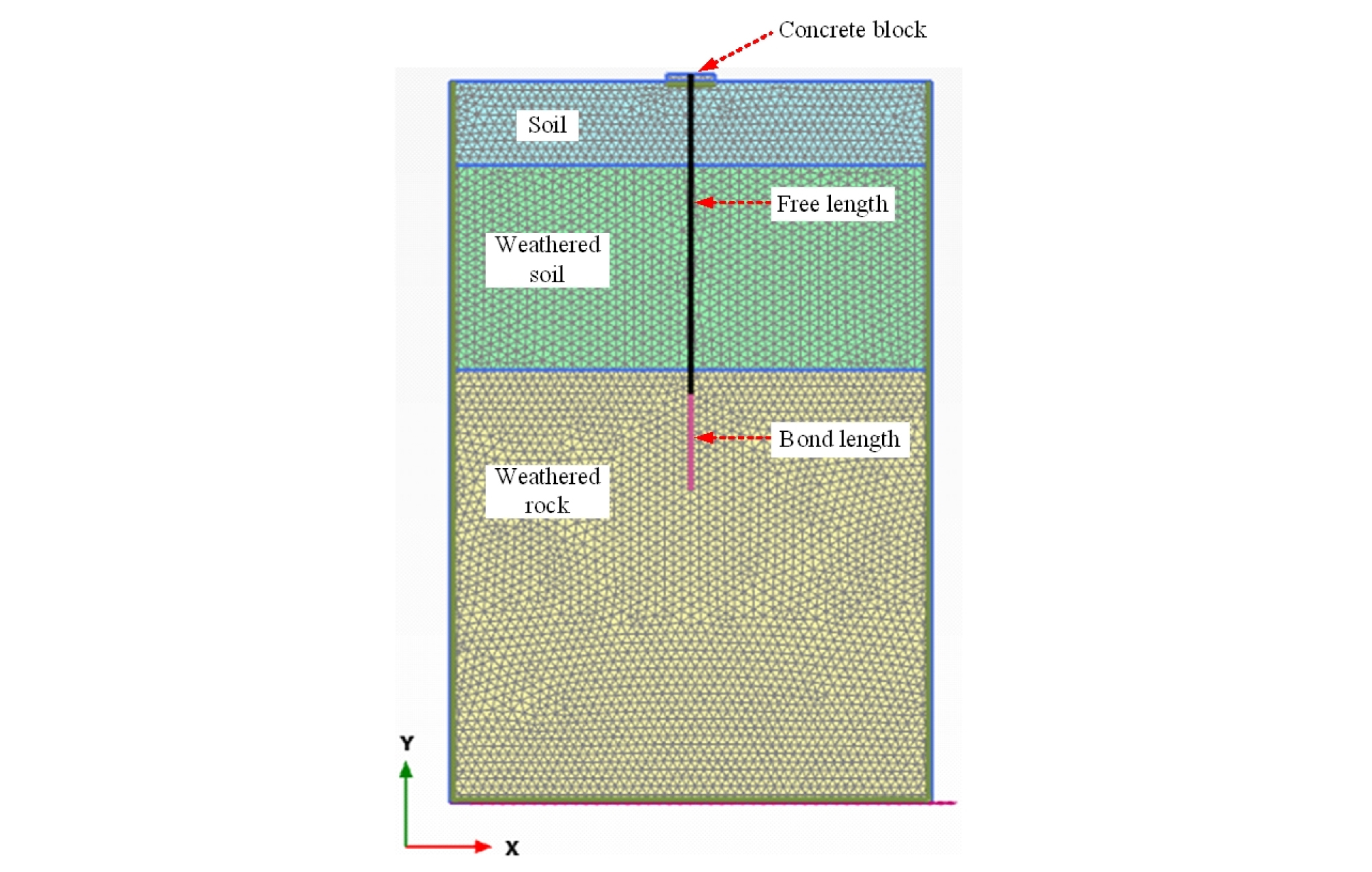
본 연구에서 사용된 유한요소해석 모델링의 메시 생성(mesh generation)을 Fig. 5에 나타내었다. 그라운드 앵커의 하중은 현장에서의 확인시험에서와 동일한 350 kN이 앵커 요소에 적용되었다.
3.3 물성치
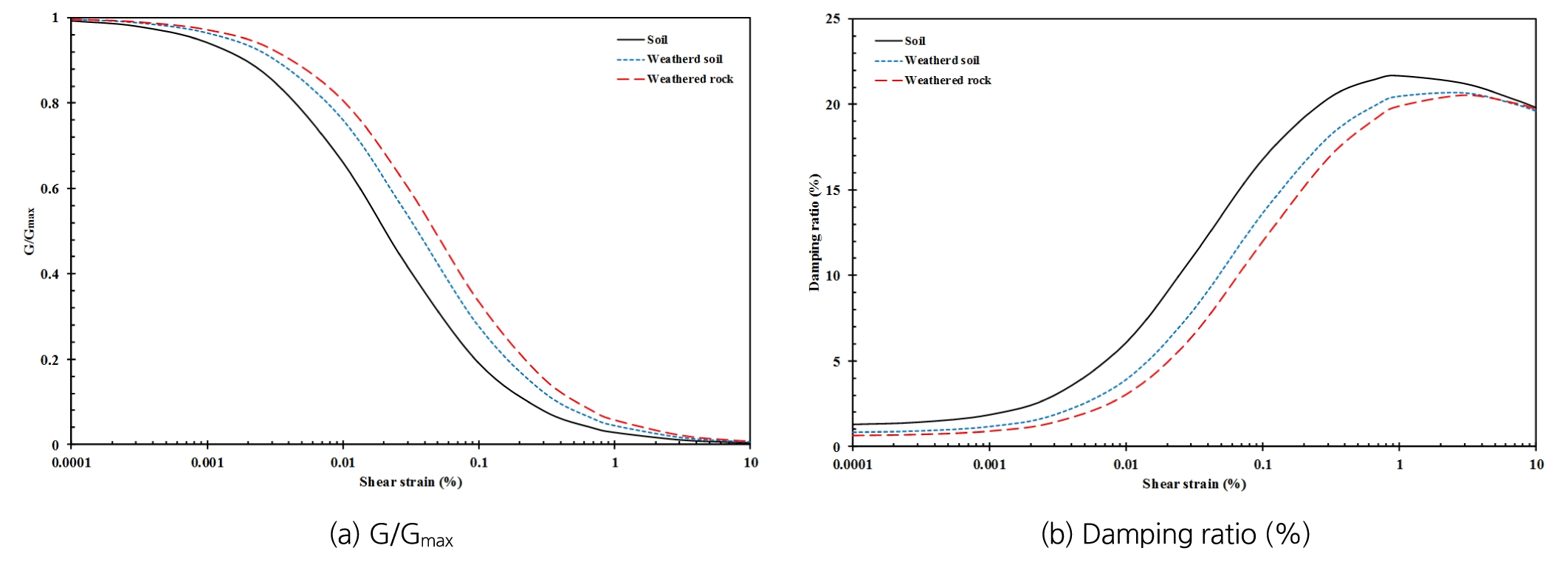
동적해석을 위해 지반의 동적물성치를 산정하여야 하며, 지반의 구성모델에 따라 그 물성치는 다르다. 본 연구에서는 수치해석시 가장 많이 사용되고 있는 Mohr-Coulomb 모델을 사용하였다. MC model을 이용한 동적해석에서 필요한 지반물성치는 지반의 점착력, 전단저항각, 전단탄성계수, 감쇠비 등이 있다. 그 중 점착력과 전단저항각은 정적해석과 동일하게 적용하고, 전단탄성계수와 감쇠비는 동적해석을 위해 추가 고려사항이 필요하다. 정적해석에서의 전단탄성계수(G)는 지반의 강성계수(E: Young’s modulus, ν: Poisson’s ratio)에 의해 결정된다. 이를 결정하는 방법은 탄성파 시험으로 측정된 Vs와 Poisson’s ratio, 지층별 전단탄성계수 감소곡선과 감쇠비 곡선을 이용한 1차원 비선형 지반응답해석을 수행하여 유효 전단변형률 주상도를 도출한 후, 이에 상응하는 깊이별 전단탄성계수와 감쇠비를 추출하여 해석에 적용하는 것이다. 본 연구에서는 이를 위해 Deepsoil(Hashash et al., 2017)을 이용하여 대상지반의 전단탄성계수를 산정하였으며, 그 결과를 Fig. 6에 나타내었다.
지반의 감쇠비 또한 동적해석에서 가장 중요한 인자 중 하나이며, 본 연구에서 사용된 Plaxis의 경우 지반요소의 감쇠효과를 Rayleigh damping coefficient (α,β)를 이용하여 고려할 수 있다. α와 β는 식 (4), (5)를 통해 산정되는데, 이를 위해 지반 및 구조물의 고유주기와 감쇠비가 결정되어야 한다. 흙 지반과 암반지반의 감쇠비는 일반적으로 5%, 1% 로 각각 고려하는데 본 대상 현장의 경우 풍화토와 풍화암으로 판정되어 5%의 감쇠비를 적용하였다.
각 지반의 고유주기는 각 지반의 전단파 속도를 이용하여 구할 수 있으며, 그 방법은 식 (5), (6)과 같다 (Yoon et al., 2006).
| $$T_g=4\times\Sigma\frac{d_i}{V_{si}}=\frac{4D}{V_s}$$ | (5) |
| $$f=\frac1{T_g}$$ | (6) |
여기서, i는 30 m까지의 지반층의 번호를 의미하여, di는 i번째 지반층의 두께, Vsi는 i번째 지반층의 전단파 속도, Tg는 지반의 고유주기, f는 지반의 고유주파수를 의미한다. D는 기반암까지의 심도이며, 본 연구에서는 기반암까지 시추조사를 수행하지 않은 관계로 30 m로 가정하였다.
수치해석에 적용된 물성치 및 감쇠비(ξ)와 f에 따라 산정된 대상현장 지반의 Rayleigh damping coefficient를 Table 1, 2에 각각 정리하였다.
Table 1. Material properties
Table 2. Rayleigh damping coefficient
| Soil | Weathered soil | Weathered rock | Concrete block | |
| α | 0.0225 | 0.0509 | 0.0783 | 0.5474 |
| β | 0.0419 | 0.0175 | 0.0124 | 0.065e-3 |
4. 결 과
4.1 반력판의 침하
앵커에 긴장력을 도입하기 위해서는 지표면에 반력판이 필요하다. 일반적으로 반력판은 철근콘크리트로 제작되지만, 현장시험 단계에서는 H-Beam등을 이용하여 제작되기도 한다. 이러한 반력판은 하부 지반의 지지력 계산을 통해 설계되지만, 일부 발생하는 침하는 앵커의 축력에 영향을 미칠 수 있다.
본 연구에서는 수치해석을 통해 실제 현장에 적용된 반력판의 size와 동일하게 모사하여, 긴장력 도입시 뿐만 아니라 지진하중이 고려될 때 발생할 수 있는 반력판의 침하에 대해 분석하였다.
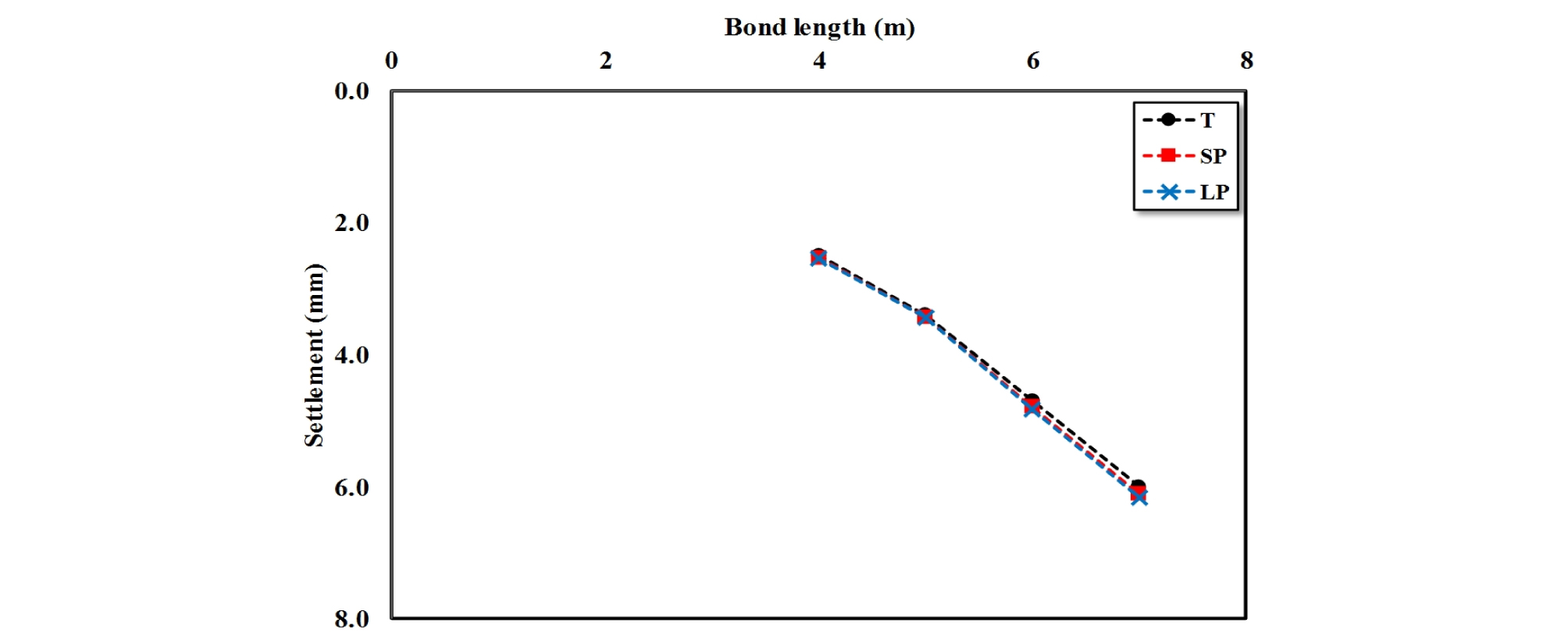
긴장력 도입단계에서 발생한 반력판의 침하를 Fig. 7에 나타내었다. Fig. 7에서의 T는 앵커에 긴장력만 도입된 상태를 의미하며, SP(Short period)는 단주기 지진이 고려되었을 때 고려하였으며, LP(Long period)는 장주기 지진이 고려된 case를 의미한다. 그림에서 알 수 있듯이, 긴장력이 도입된 단계에서는 정착부의 길이가 4 m일 경우 2.5 mm의 침하가 발생하였으며, 5 m 일 때 3.4 mm, 6 m 일 때 4.7 mm, 7 m 일 때 6.0 mm가 발생하였다. 이후 단주기 지진이 고려되었을 때 정착장이 4 m 일 때 2.53 mm, 5 m 일 때 3.44 mm, 6 m 일 때 4.79 mm, 7 m 일 때 6.11 mm가 발생하였으며, 장주기 지진이 고려되었을 때, 4 m 일 때 2.54 mm, 5 m일 때 3.44 mm, 6 m 일 때 4.83 mm, 7 m 일 때 6.16 mm가 발생하였다. 이를 통해 지진하중으로 인해 발생하는 반력판의 침하는 주기가 클수록 추가 침하가 크게 발생하지만 정착장이 짧을 경우 그 차이는 거의 없으며, 정착장이 6 m 이상이 되면 그 차이가 점점 커지는 것을 알 수 있었다.
이러한 반력판의 경우 시험용 앵커에만 적용되는 구조물로 실제 사용되는 구조물의 경우 구조물의 기초라 할 수 있다. 기초의 크기와 형식에 따라 다르지만, 실제 구조물의 안정성을 확보하기 위해 그라운드 앵커가 적용된 경우 그 구조물의 침하는 반력판의 침하보다 크게 발생될 수 있으므로 추후 실내모형시험 및 수치해석을 통해 앵커가 적용된 실제 구조물의 지진하중에 따른 침하 특성을 검토 및 분석할 예정이다.
4.2 정착부 수직변위
정착부의 변위는 긴장력 도입 단계, 단주기 지진하중, 장주기 지진하중 발생 각각의 단계에서 발생한 수직변위(δV)와 수평변위(δH)로 구분하여 분석하였다.
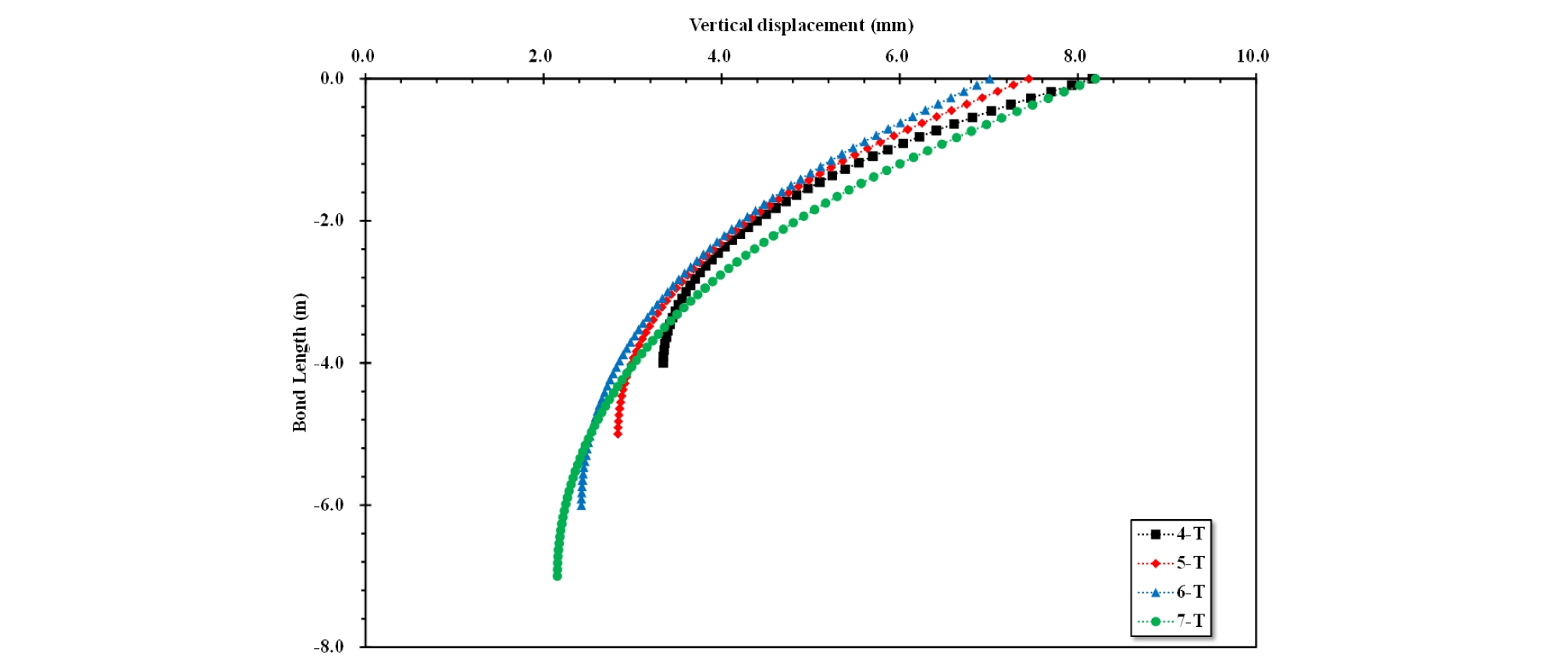
긴장력 도입단계에서 정착부 길이(4-T, 5-T, 6-T, 7-T)에 따른 정착부 최대수직변위는 천단부(Top)에서 발생하였으며 8.16 mm, 7.45 mm, 7.01 mm, 8.2 mm로 나타났다. 또한 정착부의 선단부(Bottom)에서는 3.34 mm, 2.83 mm, 2.42 mm, 2.15 mm의 수직변위가 발생하는 것으로 나타나, 정착부의 천단부에 비해 작은 변위가 발생하는 것을 알 수 있었다(Fig. 8).
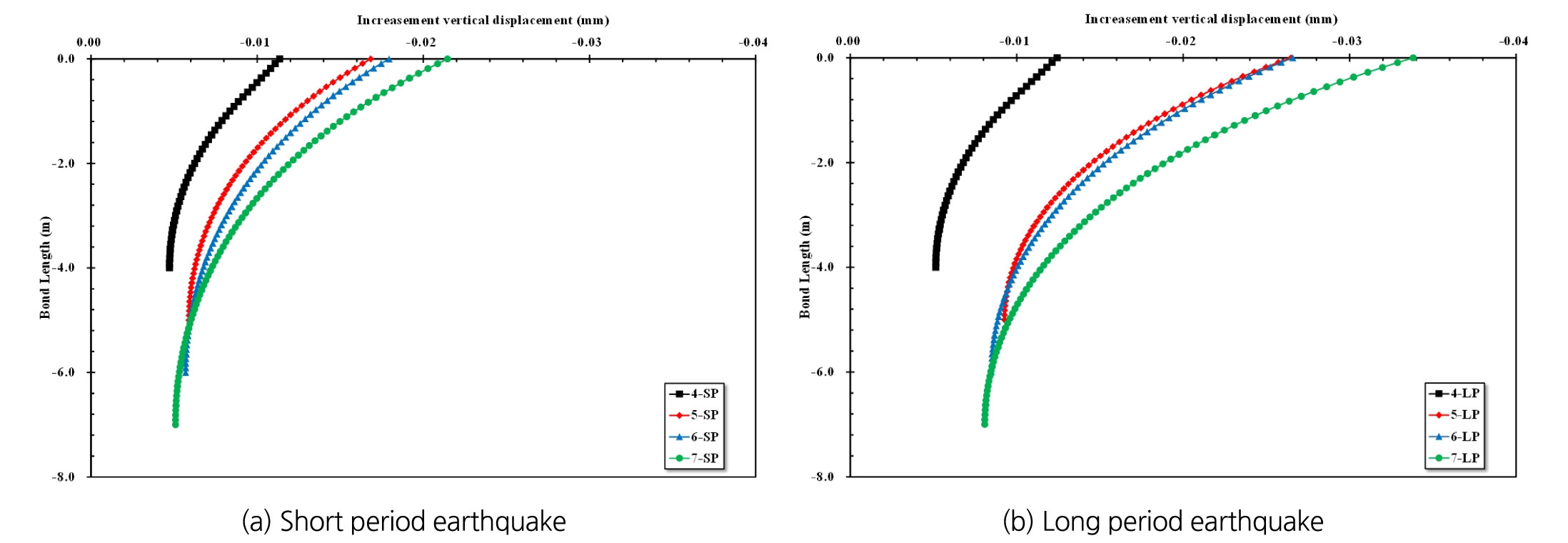
정착부의 길이가 4 m일 경우 0.011 mm, 5 m 일 때 0.017 mm, 6 m 일 때 0.018 mm, 7 m일 때 0.021 mm의 최대수직변위가 추가로 발생하였으며, 장주기 지진에서는 정착장이 4 m 일 때 0.012 mm, 5 m 일 때 0.026 mm, 6 m 일 때 0.027 mm, 7 m 일 때 0.034 mm가 발생하는 것으로 나타났다. 지진하중이 고려되었을 때 발생하는 추가 수직변위의 경우 또한 정착부의 위치에 따라 다르게 나타났으며, 모든 case에서 정착부 천단에서 최대수직변위, 선단에서 최소수직변위가 발생하였다. 지진하중에 의해 정착부 선단에서 발생한 추가 수직변위는 모든 정착길이 case에서 0.005 mm~0.009 mm로 발생하여 그 차이가 크지 않은 것을 알 수 있었다. 단주기 및 장주기 지진하중이 고려되었을 때 발생한 정착부의 각 지점에서 발생한 추가 수직변위를 Fig. 9에 각각 나타내었다. 정착부에서 발생하는 변위는 긴장력 도입단계에서부터 천단부에서 가장 크게 발생하는 것을 알 수 있다. 이는 본 연구에서 고려된 앵커의 정착방식에 기인한 것으로 판단된다. 본 연구에서 고려된 마찰인장형 앵커의 경우 정착부의 천단부에서 가장 큰 응력이 발생하며, 이로 인해 천단부에서의 변위가 가장 크게 발생하며, 축력 또한 천단부에서 가장 큰 것으로 판단된다.
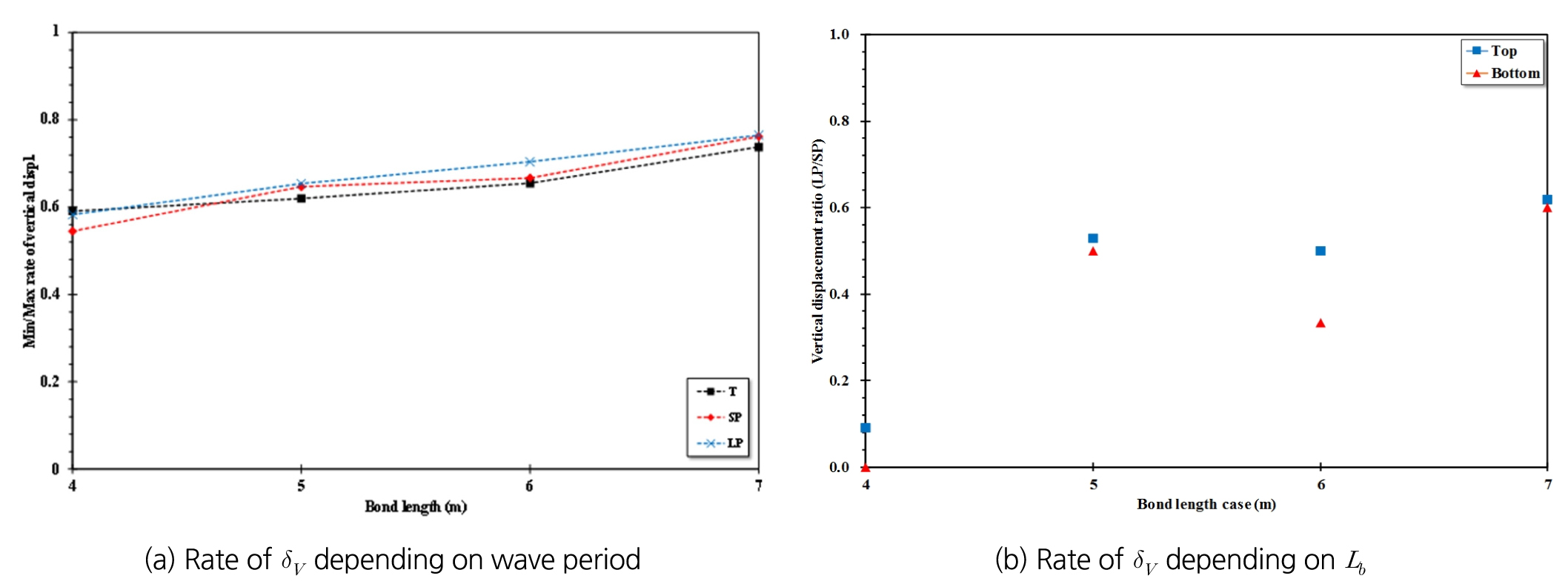
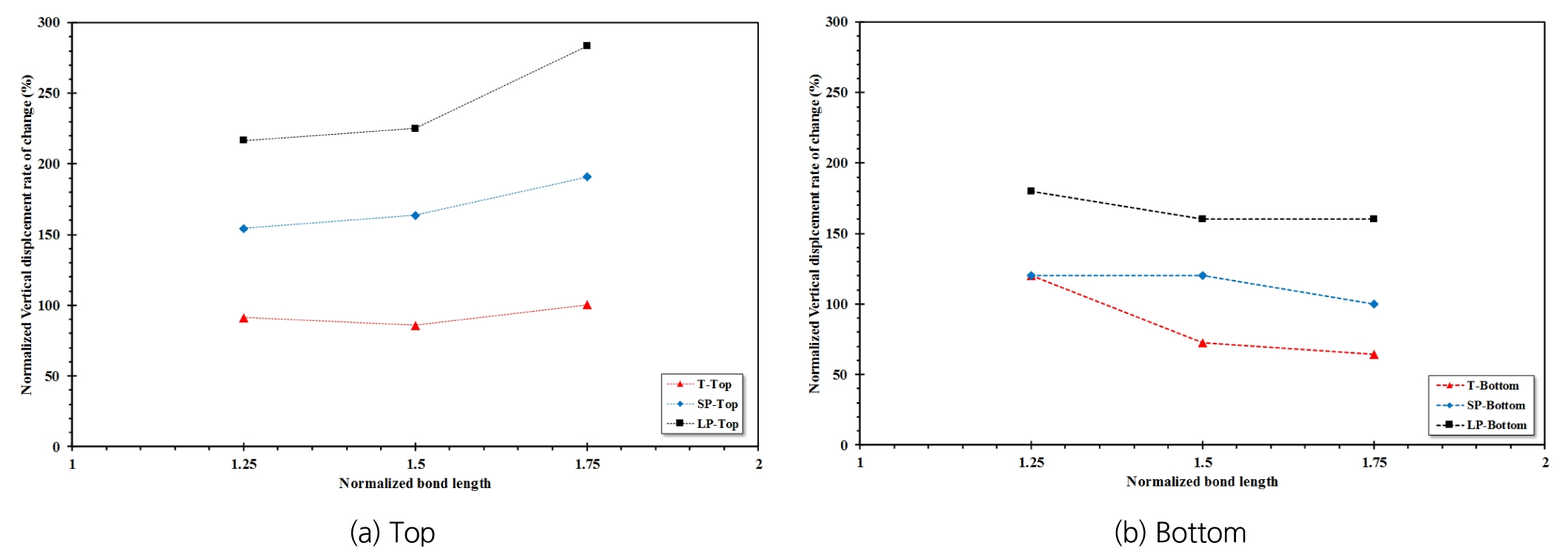
앞에서 분석한 것과 같이, 정착부의 천단과 선단에서 각기 다른 변위가 발생하는 것을 알 수 있었다. 정착부 내에서 발생하는 최소/최대 변위의 비율(δV-Min/δV-Max)은 긴장력 도입단계(T)에서 정착부의 길이가 4 m일 경우 59.1%, 5 m일 때 62%, 6 m 일 때 65.5%, 7 m일 때 73.8%로 정착부 길이가 증가할수록 그 비율이 큰 것을 알 수 있었으며, 장주기 지진이 발생할 때 그 차이가 가장 큰 것으로 나타났다. 이러한 차이는 단주기 및 장주기 지진이 발생하였을 경우 모두 유사하게 나타났다 (Fig. 10(a)).
단주기 지진과 장주기 지진에 의한 정착부 천단 수직변위 증가율을 비교하였을 때, 정착부 길이가 4 m이 경우 장주기 지진으로 인해 발생된 수직변위가 단주기 지진에 비해 약 9.1% 크게 나타났으며, 5 m 일 때 52.9%, 6 m 일 때 50.0%, 7 m 일 때 약 61.9%로 나타나 정착부 길이가 길수록 지진의 주기가 길수록 정착부에서 발생하는 수직변위의 증가는 커지는 것으로 나타났다. 이는 정착부 선단에서도 유사한 경향으로 나타났다 (Fig. 10(b)).
정착부의 천단과 선단에서 발생한 수직변위의 변화율을 정규화하여 Fig. 11에 나타내었다.
Fig. 11에서 알 수 있듯이, x축은 정착부 길이가 1 m씩 증가하는 것을 4 m기준으로 정규화하였며, y축은 4 m일 때의 수직변위를 기준으로 정규화하였다. 그 결과 길이가 길어질수록 정착부 천단에서 발생하는 변위 증가가 큰 것으로 발생하였는데 이는 정착부 길이가 길수록 도입된 긴장력이 크기 때문인 것으로 판단된다. 하지만 정착부의 선단의 경우, 정착부 길이가 길수록 변화율이 감소하는 것을 알 수 있었다. 뿐만 아니라 지진하중에 따라 발생되는 정착부의 수직변위는 선단에 비해 천단에서 크게 발생되는 것을 알 수 있었다.
4.3 정착부 수평변위
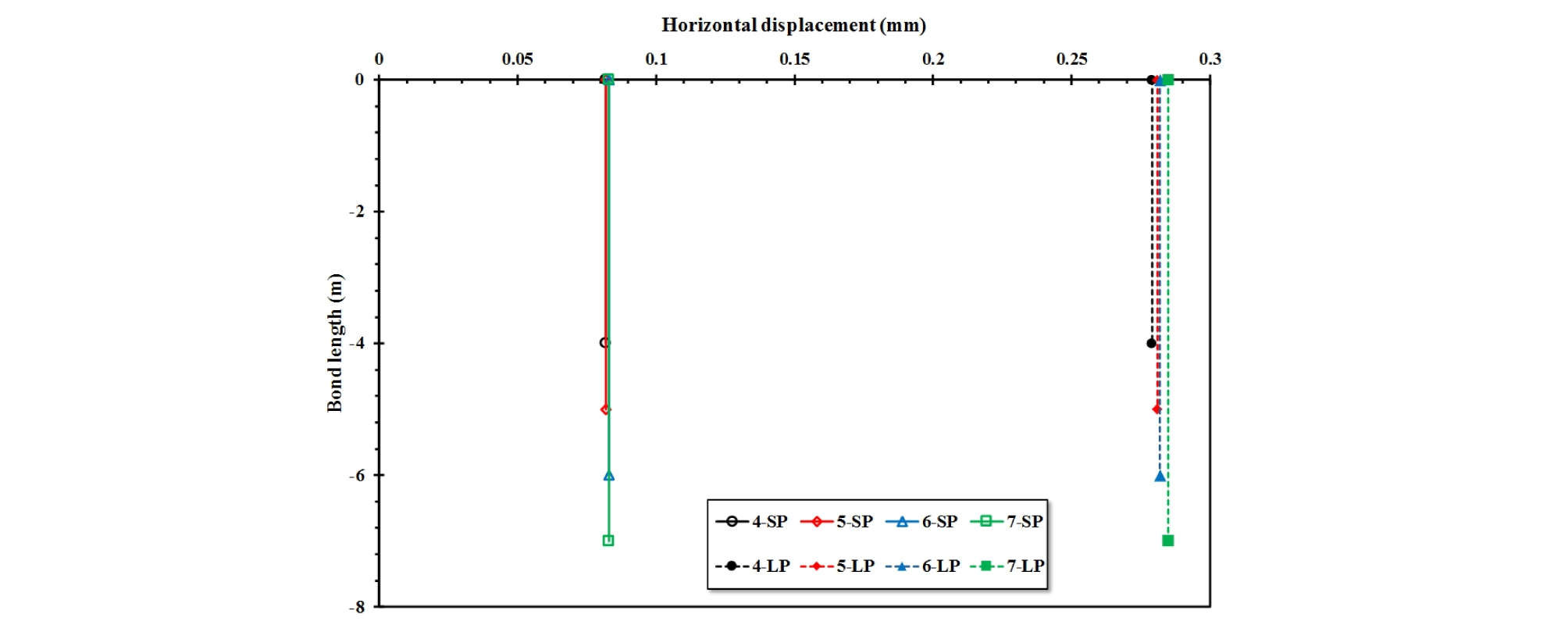
정착부의 수평변위(δH)는 긴장력이 도입된 단계(T)에서는 발생하지 않았지만, 지진하중에 의해 수평변위가 발생하였다. 수평변위의 경우 정착부 천단과 선단의 차이는 매우 미미하였다. 단주기 지진에 의해 발생된 앵커 정착부의 수평변위는 Lb가 4 m~7 m일 때 0.082 mm~0.083 mm가 발생하였다. 반면, 장주기 지진에 의해 발생된 정착부 수평변위는 0.279 mm~0.285 mm가 발생하였다. 길이에 따른 정착부의 차이는 크게 나지 않았지만, 지진의 주기가 클 경우 짧은 경우에 대비 약 3.4배 가량 크게 발생하였다 (Fig. 12).
정착부에서 발생된 수직 및 수평변위는 정착부를 구성하는 강연선과 그라우트체 중 그라우트에 균열을 발생시킬 수 있으며, 이는 앵커의 잔존긴장력을 감소시키게 된다. 이러한 잔존긴장력의 감소는 정착부의 변위 뿐만 아니라 반력판의 침하, 앵커 두부의 변위 등 다양한 원인에 의해 발생할 수 있는 것으로 알려져 있다. 수치해석을 통해 정착부 변위와 잔존긴장력 감소의 관계를 분석하기 어려우므로, 실내모형시험을 통하여 분석할 예정이다.
4.4 정착부 축력
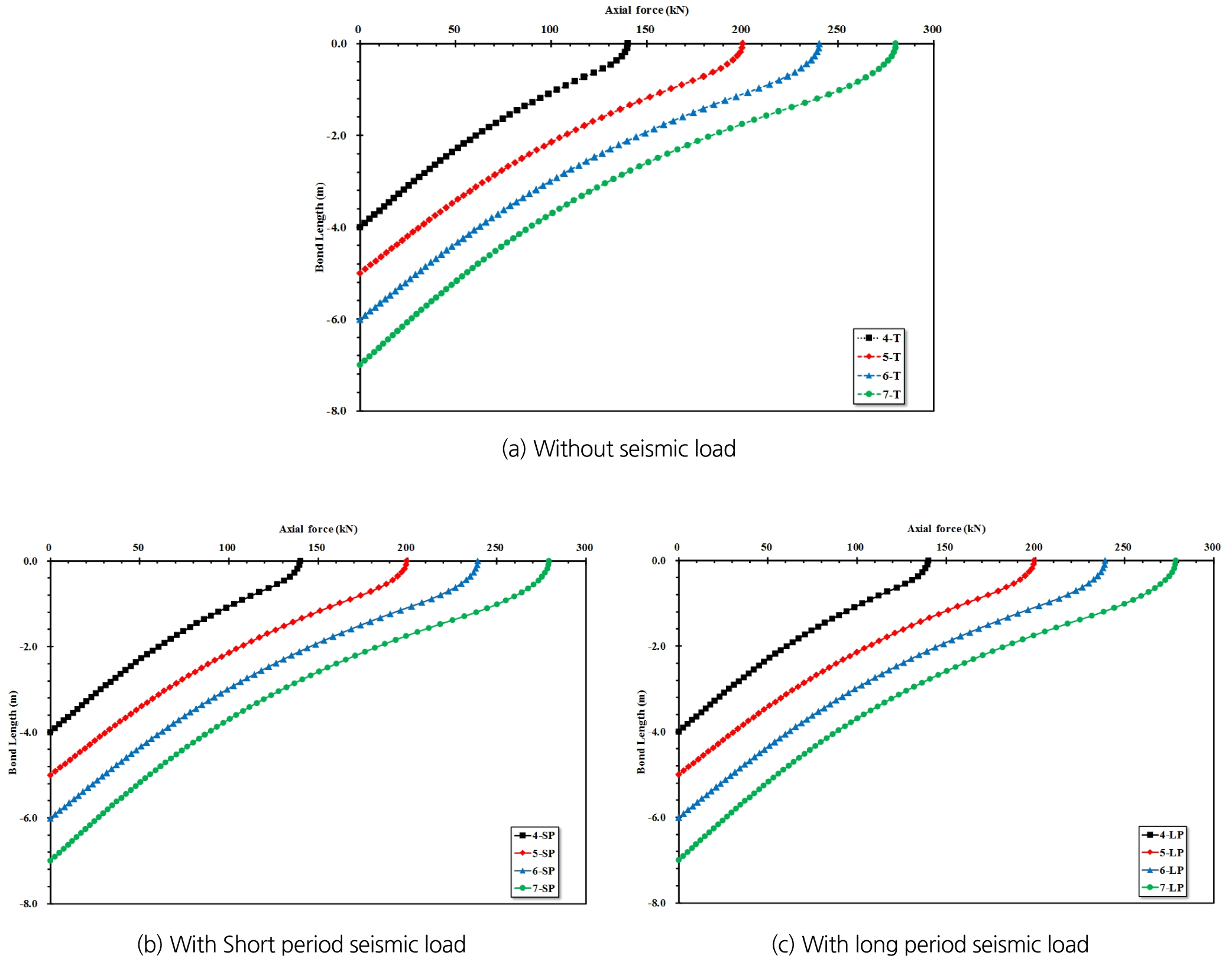
지진하중을 고려한 그라운드 앵커의 정착부 축력에 대해 분석하였다(Fig. 13). 그라운드 앵커의 축력은 각각의 case에 도입된 긴장력에 따라 크기가 측정되었다. 현장시험과 동일한 긴장력을 도입한 case인 경우 T-4인 경우 140 kN의 축력이 발생하였으며, 500 kN, 600 kN, 700 kN일 경우에는 200 kN, 240 kN, 280 kN의 축력이 발생하는 것으로 나타났다. 이는 정착부에 작용하는 축력으로인해 반력판의 침하 및 강연선에 도입된 축력과 그라우트에 발생하는 축력의 차이로 인해 발생하는 것으로 판단된다.
긴장력이 도입된 이후 지진하중을 고려하였을 때의 축력의 변화를 Fig. 13 (a), (b)에 나타내었으며, 지진의 주기특성에 관계 없이 앵커의 축력은 감소하는 것으로 나타났다. 지진하중으로 인해 축력의 감소율은 다소 차이가 있었으며 단주기 지진에 비해 장주기 지진일 경우 축력이 감소하는 경향이 다소 크게 나타났다. 단주기 지진이 발생하였을 때 정착부의 길이가 4m인 경우 약 0.1%가 감소하였으며, 5 m 일 때 0.3%, 6 m일 때 0.4%, 7 m 일 때 0.5%가량 감소하는 것으로 나타났다. 장주기 지진이 고려되었을 경우 정착부의 길이가 4 m일 때 0.2%, 5 m 일 때 0.5%, 6 m 일 때 약 0.5%, 7 m 일 때 약 0.6% 감소하는 것으로 나타났다.
4 m의 앵커 정착부 길이(Lb)를 기준으로 1.25Lb, 1.5Lb, 1.75Lb로 증가함에 따라 축력은 약 43%, 71%, 100% 증가하였으며, 이는 단주기 지진하중 및 장주기 지진하중을 고려한 경우에도 유사하게 나타났다. 따라서 정착부의 축력은 지진하중의 주기 특성 보다는 길이에 민감한 것으로 판단되었다.
앵커의 축력변화는 실제 앵커의 잔존긴장력을 의미하며, 이는 앵커의 상태를 분석하는데 가장 중요한 기준이 된다. 본 연구는 그라운드 앵커 정착부의 지진하중으로 인한 거동 특성에 관한 기초적인 연구이며, 추후 실내모형시험 및 수치해석을 통해 다양한 지진의 주기 특성 및 지반조건에 따른 정착부의 잔존긴장력을 포함한 거동 특성을 정량적으로 평가할 예정이다. 현재 실내모형시험 토조가 제작 중에 있으며, 현장시험 또한 계획 중에 있다.
5. 결 론
본 연구에서는 그라운드 앵커의 현장시험을 수행하였으며, 이를 수치해석으로 모사하여 지진이 발생되었을 때 앵커의 거동 특성을 분석하였다. 수치해석에 고려된 지진하중은 단주기 지진과 장주기 지진으로 구분하여 적용하였으며, 그에 따른 반력판의 침하, 정착부의 수직 및 수평변위, 축력의 변화 등을 분석하였다.
1) 지진하중으로 인해 발생하는 반력판의 침하는 주기가 클수록 추가 침하가 크게 발생하지만 정착장이 짧을 경우 그 차이는 거의 없으며, 정착장이 6m 이상이 되면 그 차이가 점점 커지는 것을 알 수 있었다.
2) 정착부의 변위는 긴장력 도입 단계, 단주기 지진하중, 장주기 지진하중 발생 각각의 단계에서 발생한 수직변위(δV)와 수평변위(δH)로 구분하여 분석하였다. 수직변위의 경우 정착부의 천단에서 최대 변위가 발생하였으며, 선단에서 최소변위가 발생하였다. 이는 앵커의 정착방식에 의한 결과로 마찰 인장형 앵커의 전형적인 거동 형태에 해당된다. 뿐만 아니라, 이러한 거동 형태는 정착부의 축력 거동 특성에서도 유사하게 나타났다.
3) 긴장력 도입 단계에서 발생된 정착부의 최대수직변위와 최소수직변위의 차이는 정착장이 클수록 증가하였으며, 지진하중으로 인해 그 차이는 증가하지만 그 증가량은 단주기 지진 보다 장주기 지진이 고려되었을 경우 더 크게 나타났다.
4) 앵커의 정착부의 축력은 지진의 주기특성에 관계 없이 감소하는 것으로 나타났다. 지진하중으로 인한 축력의 감소율은 다소 차이가 있었으며 단주기 지진에 비해 장주기 지진일 경우 축력이 감소하는 경향이 다소 크게 나타났다.